Nouveautés pour les études et les solveurs
Prise en charge des GPU NVIDIA®
L'utilisation du GPU est désormais possible pour les calculs de pression acoustique et l'entraînement des modèles de substitution. Cette fonctionnalité est disponible pour les systèmes équipés d'un GPU NVIDIA® compatible.
Accélération GPU pour les calculs de pression acoustique explicite en temps
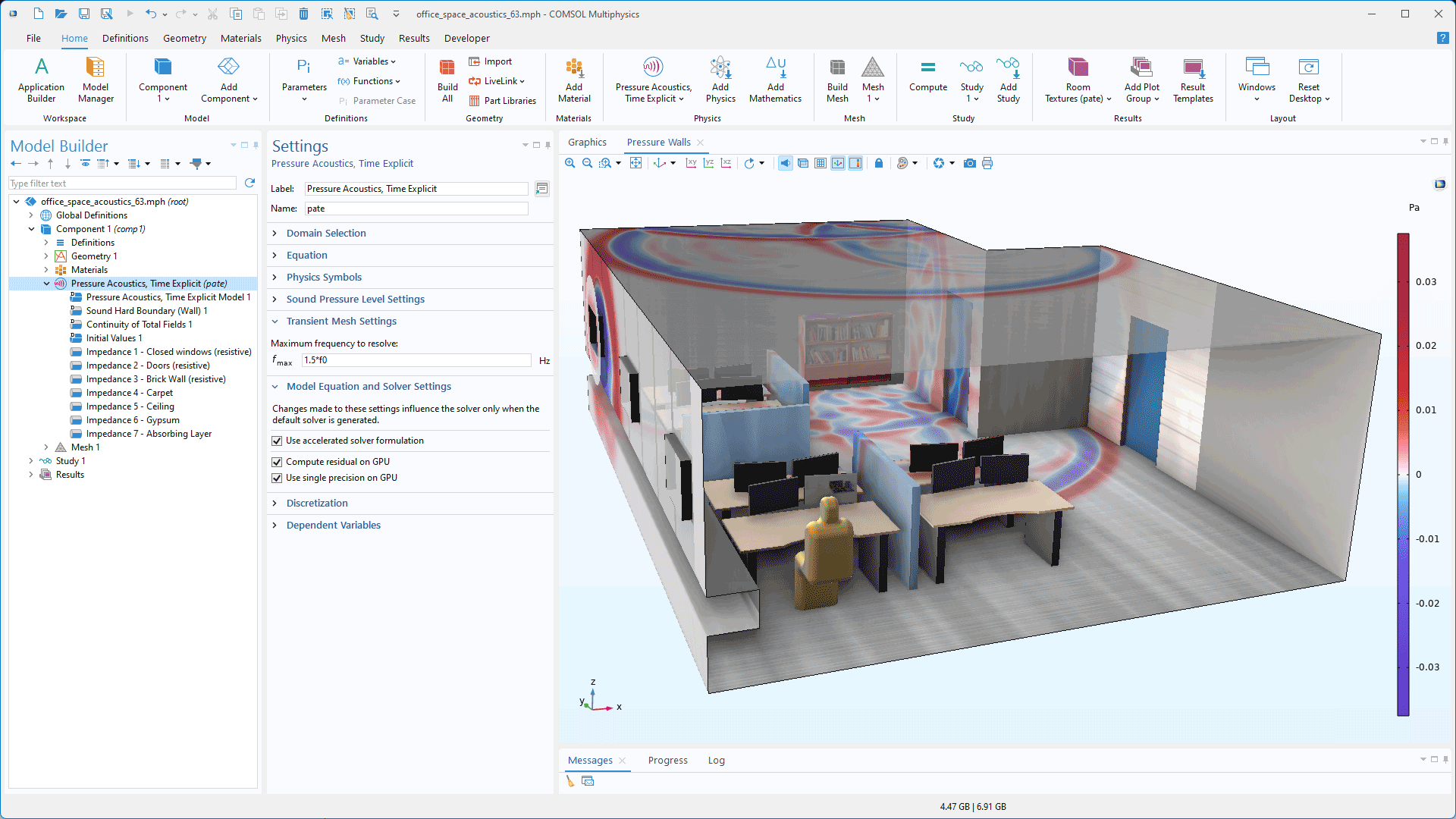
Les modèles linéaires de pression acoustique explicite en temps peuvent désormais être résolus à l'aide d'une formulation accélérée compatible avec des conditions aux limites d'impédance réalistes. Cette accélération peut être considérablement accrue lorsque la formulation est utilisée avec une carte GPU NVIDIA®, bien que le gain de performance dépende du matériel. Pour activer cette fonctionnalité, CUDA® Toolkit doit être installé (son chemin d'accès pouvant être spécifié lors de l'installation.) Cette fonctionnalité est illustrée dans le tutoriel Acoustics of an Open-Plan Office Space. Pour plus de détails, consultez les nouveautés du module Acoustics.
Accélération GPU pour l'entraînement des modèles de substitution de type DNN
La prise en charge du GPU pour l'entraînement des modèles de substitution de type DNN a été ajoutée, ce qui accélère considérablement le processus d'entraînement et permet un développement plus rapide des modèles de substitution destinés aux applications et à divers contextes de simulation. Pour activer cette fonctionnalité, assurez-vous que l'option CUDA DNN Support est sélectionnée sur la page Produits de l'installateur COMSOL. Par ailleurs, le NVIDIA® CUDA® Toolkit doit être installé et peut être téléchargé sur le site Web de NVIDIA®.
Amélioration de la génération des données du modèle de substitution
La génération de données dépendant de l'espace, du temps et de la fréquence destinées à l'entraînement des modèles de substitution de type DNN est désormais beaucoup plus facile.
Une option Échantillonnage géométrique est accessible depuis le nouveau sous-menu Échantillonnage du modèle de substitution dans les Définitions des composants du modèle. Cette fonctionnalité permet d'échantillonner des données directement sur des domaines, des frontières, des arêtes ou des points, sans avoir à exporter ou à importer des fichiers.
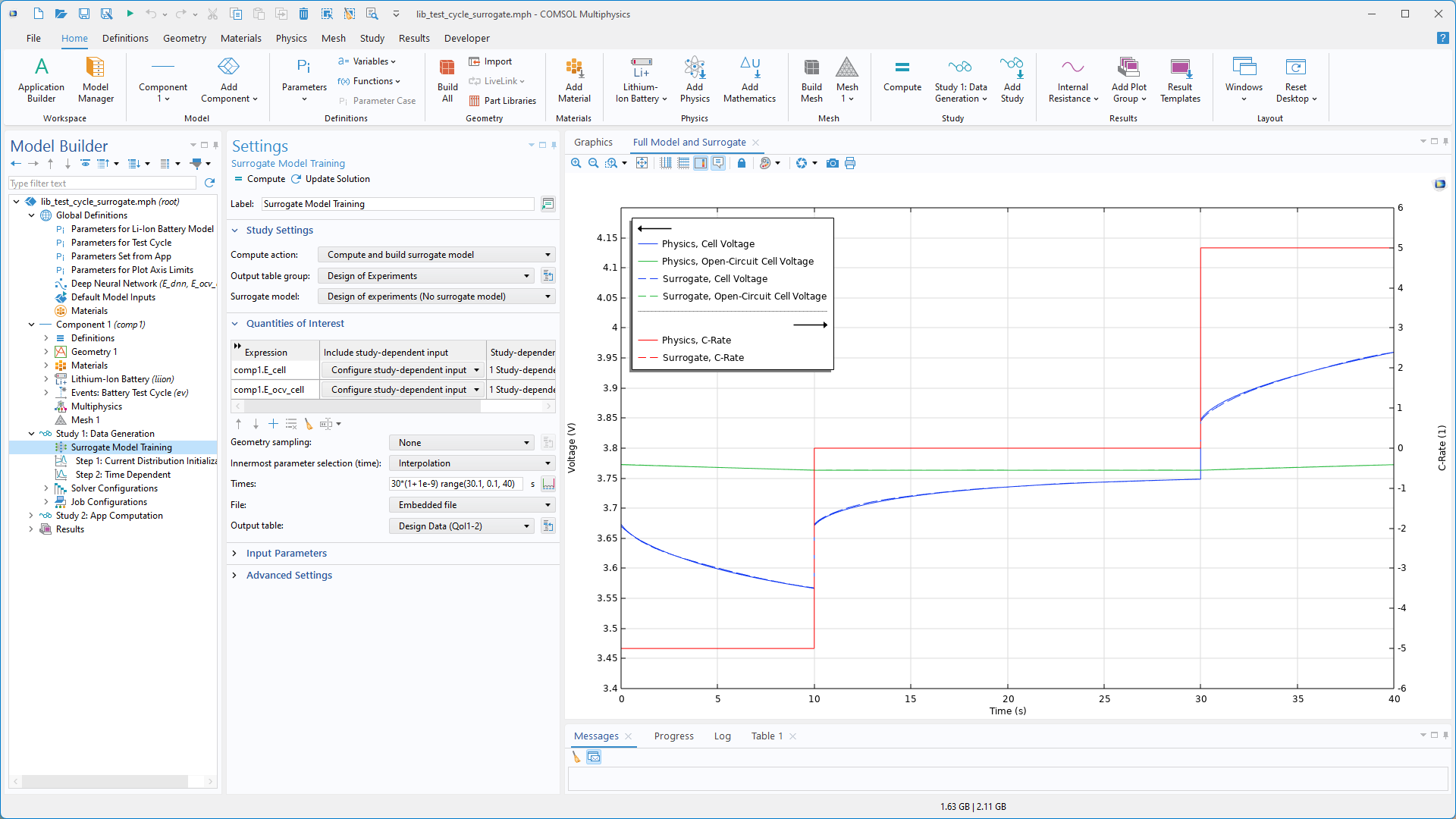
En outre, une nouvelle option Entrée dépendant de l'étude dans l'étude Apprentissage du modèle de substitution permet d'inclure des résultats de balayage en fonction du temps ou de la fréquence dans les données d'entraînement. Cela simplifie la prise en compte de données dynamiques ou dépendant de la fréquence dans les modèles de substitution.
Optimisation
Solveur adjoint de type discret
Un nouveau type de solveur adjoint Temporel discret est disponible pour le contrôle optimal et l'estimation de paramètres dépendant du temps. Ce type de solveur est basé sur une méthode de sensibilité discrète, qui offre une meilleure robustesse, une meilleure précision et des performances plus rapides pour l'optimisation par gradient avec le Solveur temporel.
Pour les problèmes d'estimation de paramètres transitoires, des améliorations significatives de la vitesse sont obtenues avec les solveurs SNOPT (sparse nonlinear optimizer) et IPOPT (interior point optimizer). Cela est dû au fait que la sensibilité agrégée de l'ensemble de l'objectif est calculée en un seul passage au lieu de calculs séparés pour chaque point de mesure. L'ancienne méthode de sensibilité continue est toujours disponible, mais elle n'est plus la méthode par défaut pour l'optimisation transitoire.
Les méthodes discrètes et continues réduisent la consommation de mémoire par le biais de points de contrôles, ce qui implique de recalculer la solution directe. De plus, il existe une nouvelle option Out-of-core qui peut être utilisée de manière alternative pour le traitement de la solution directe, afin d'utiliser temporairement l'espace disque et ainsi éviter de recalculer la solution.
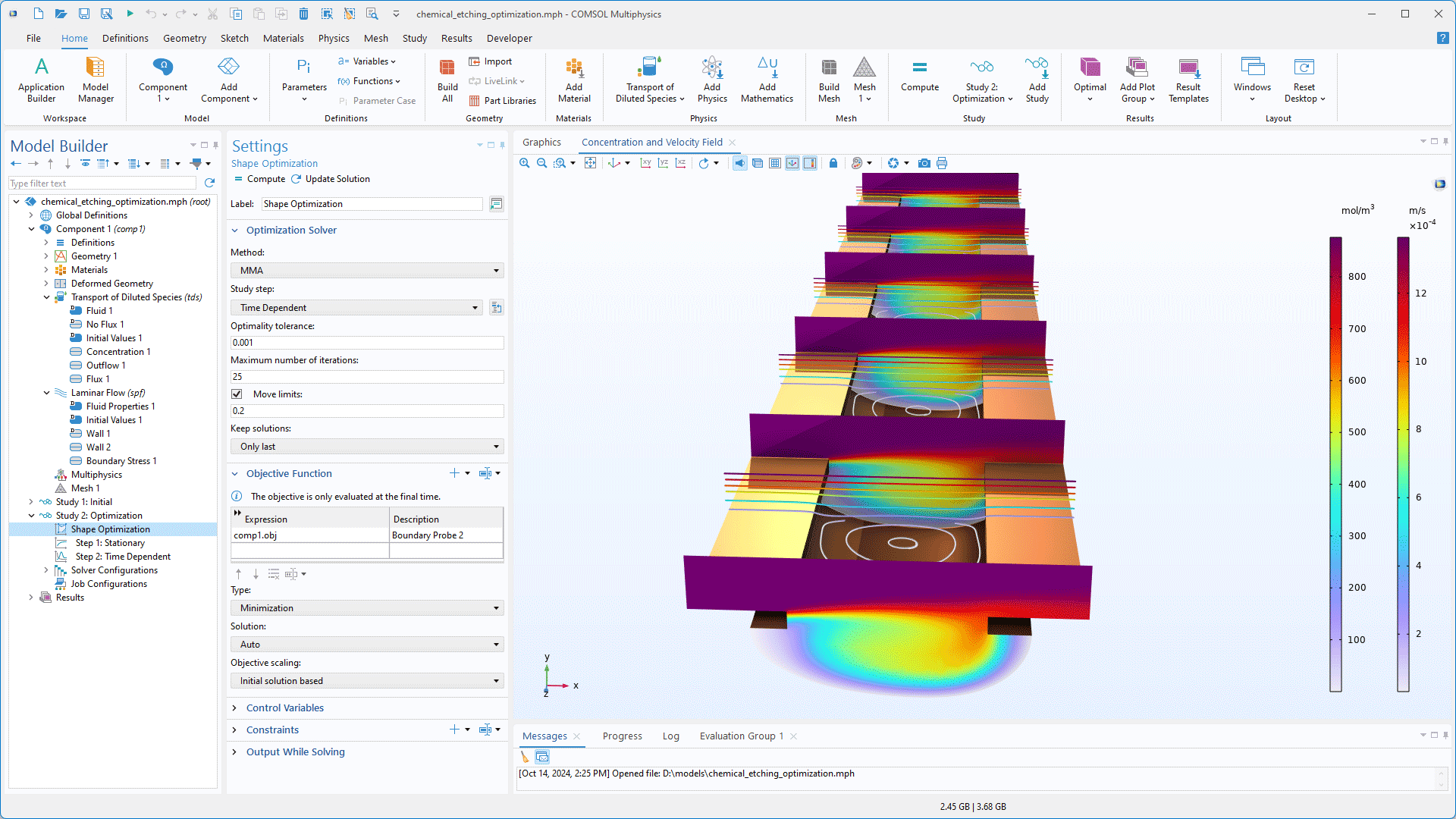
Efficient Global Optimization
Un nouveau solveur d'optimisation sans gradient qui utilise l'algorithme EGO (Efficient Global Optimization) a été introduit. Ce solveur est tout indiqué pour résoudre les problèmes d'optimisation comportant plusieurs optimums locaux, car il ne requiert pas d'estimation initiale des paramètres de contrôle et est moins susceptible d'être piégé dans un minimum local — ce qui le rend particulièrement utile pour les problèmes d'optimisation difficiles, tels que ceux impliquant des analyses dans le domaine fréquentiel.
Bien que le solveur EGO soit plus lent que les méthodes d'optimisation locale en raison de sa stratégie de recherche globale, il présente une robustesse importante lorsqu'il s'agit de naviguer dans des espaces de solutions complexes. Après avoir exécuté le solveur EGO, il est recommandé de poursuivre le traitement des résultats à l'aide d'une méthode d'optimisation locale afin d'affiner la solution. En outre, le solveur permet d'inspecter le modèle de substitution sous-jacent utilisé pour l'analyse, ce qui permet de mieux comprendre le processus d'optimisation.
Solveur aux valeurs propres non linéaires et amélioration du tri
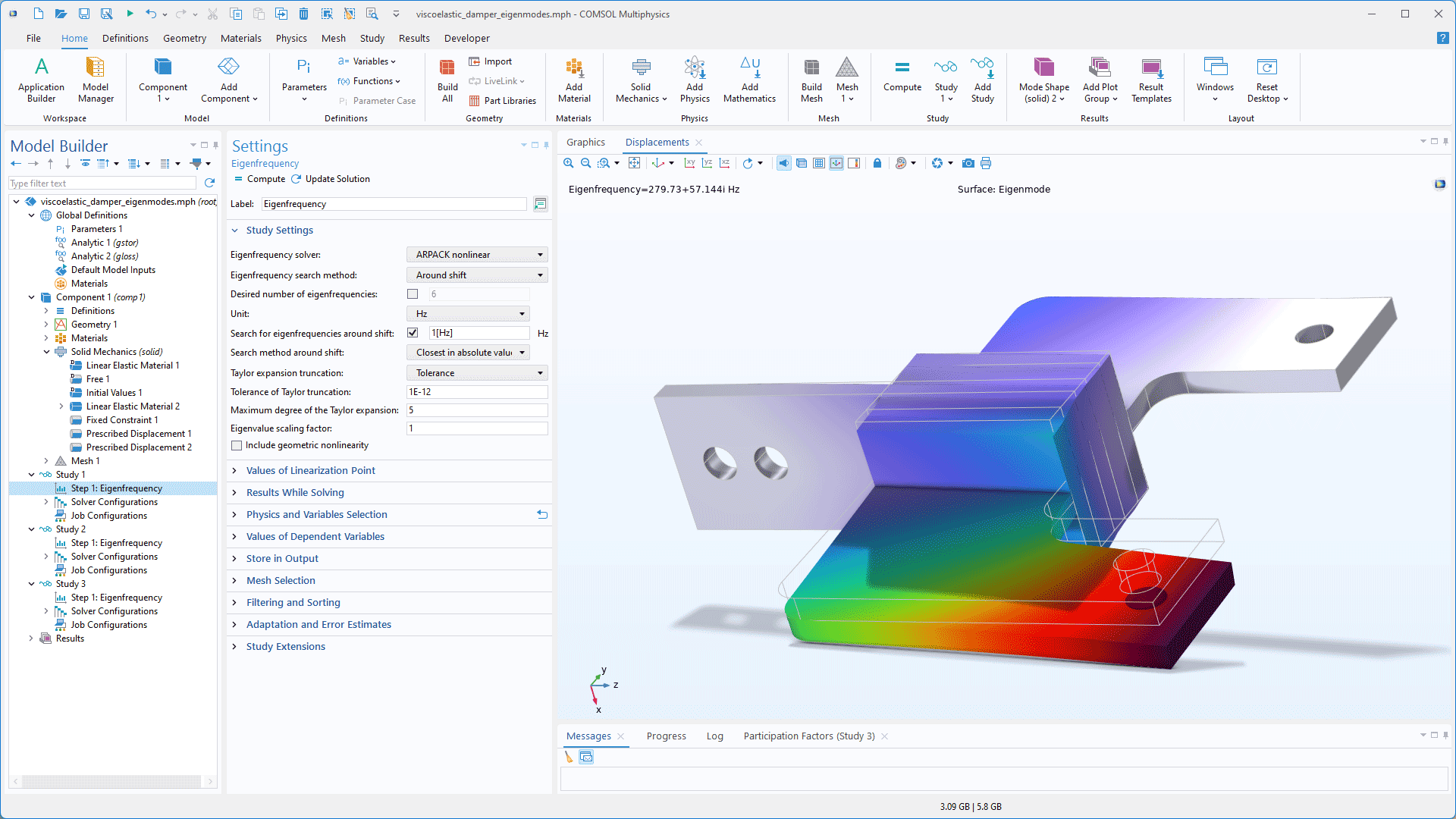
Un nouveau solveur aux valeurs propres non-linéaires basé sur la bibliothèque ARPACK est désormais disponible en option dans le solveur aux valeurs propres, éliminant le besoin d'itérations manuelles lors de la résolution de valeurs propres non linéaires. Cette option est utile dans le cas d'analyses structurelles avec des matériaux viscoélastiques, d'analyses de modes électromagnétiques, etc.
En outre, une nouvelle section Filtrage et tri a été ajoutée aux réglages des étapes d'étude Valeur propre, Fréquence propre et Analyse de mode sur frontière. Elle permet d'appliquer des expressions de filtrage, telles que real(freq) + 1e-6 > 0, et de trier les solutions propres selon divers critères, tels que les parties réelles ou imaginaires, les amplitudes ou valeurs absolues, par ordre croissant ou décroissant. Les options de tri sont également disponibles dans les noeuds de fonctionnalités Solveur aux valeurs propres et Combiner les solutions lorsque l'on travaille avec des solutions de type valeurs propres.
Modèle d'ordre réduit par décomposition orthogonale aux valeurs propres (POD)
Une nouvelle technique de réduction de modèle, POD, a été ajoutée. Le principe de la méthode POD est d'utiliser des instantanés d'un modèle pour effectuer une décomposition d'un champ physique au moyen de concepts issus de l'analyse en composantes principales. La méthode POD peut être utile pour les problèmes paramétrés dans le domaine fréquentiel.
Améliorations des solveurs
Tolérance adaptative pour les solveurs linéaires
Lors de la résolution de problèmes non-linéaires, il est désormais possible de faire varier de manière adaptative la tolérance du solveur linéaire. Cela peut conduire à des accélérations substantielles. Cette méthode utilise l'estimation d'erreur du solveur non-linéaire pour résoudre avec une précision plus faible lorsque l'on est loin de la solution et une précision plus élevée lorsque l'on approche de la convergence. La tolérance adaptative du solveur linéaire est supportée pour la méthode d'amortissement Constant. Elle est également prise en charge avec la méthode de pseudo-pas de temps couramment utilisée pour les problèmes de CFD stationnaires.
Mise à l'échelle de la méthode AMG (Algebraic Multigrid)
La mise à l'échelle des lignes pour la méthode AMG peut maintenant être définie automatiquement. L'activation de l'option Equilibrage des lignes dans le noeud Avancé du Solveur stationnaire se traduira par la détermination automatique d'une échelle appropriée pour le solveur multigrille.
