
L’analyse de fréquences propres fait partie intégrante de la boîte à outils de la modélisation numérique. Les modes propres d’un système linéaire présentent souvent des caractéristiques qualitatives distinctes, telles que la fréquence, qui évoluent différemment sur une plage de paramètres, comme la fréquence. On nous demande souvent s’il y a un moyen de suivre et de catégoriser ces familles de solutions de modes propres dans le cadre du balayage paramétrique. Dans cet article de blog, nous montrerons comment réaliser cela en utilisant une intégrale de recouvrement des modes dans le logiciel COMSOL Multiphysics®.
Modes propres et intégrale de recouvrement
Quiz: Qu’ont en commun la conception d’un câble de fibre optique pour des systèmes de communication nouvelle génération, l’optimisation du design d’un pont pour minimiser les résonances mécaniques non désirées et le perfectionnement de l’aménagement acoustique de votre salon ?
Dans chaque scénario, il est nécessaire d’avoir une bonne compréhension des modes propres du système. Les modes propres, tout comme leurs valeurs propres associées — aussi appelées fréquences propres — décrivent la réponse d’un système linéaire à des excitations externes et jouent de fait un rôle crucial dans l’élaboration de son design. Dans certains cas, nous voulons maximiser le couplage avec un ou quelques modes propres, comme pour un filtre à cavité pour les communications radiofréquences ou pour un haut-parleur. Dans d’autres situations, le couplage à ces modes de résonance peut avoir des conséquences catastrophiques, comme l’effondrement d’un pont.
Dans le cadre d’un balayage paramètrique, les modes et fréquences propres changent naturellement lorsque nous ajustons les paramètres de notre système, tels que la fréquence de fonctionnement ou les dimensions géométriques. Cependant, ces modes conservent souvent une certaine ressemblance sur le plan qualitatif. Prenons un exemple simple, une équation d’onde sur une membrane elliptique 2D — comme la surface d’une peau de tambour en vibration ou une plaque de Chladni.
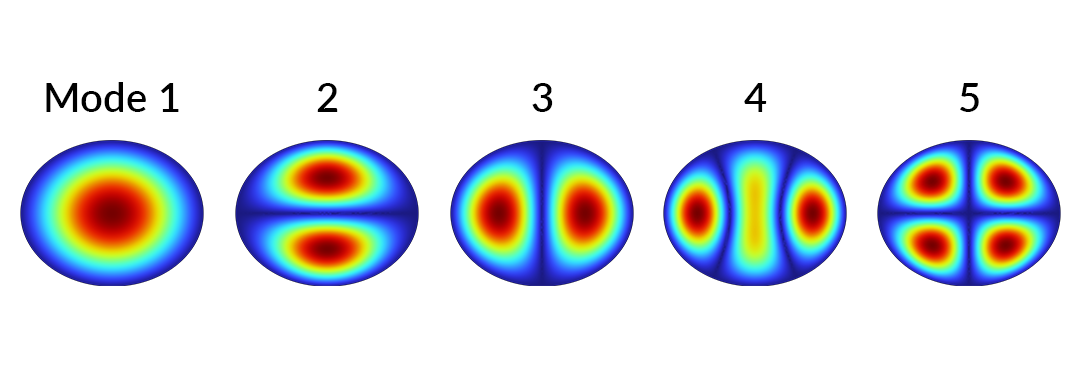
Les cinq premières solutions de modes propres de l’équation d’onde 2D sur une membrane elliptique avec des frontières fixes.
Une étude de fréquences propres révèle les cinq premiers modes propres dont l’amplitude des déplacements est représentée ci-dessus. Maintenant, supposons que nous voulions réaliser un balayage sur le demi-axe vertical de l’ellipse.
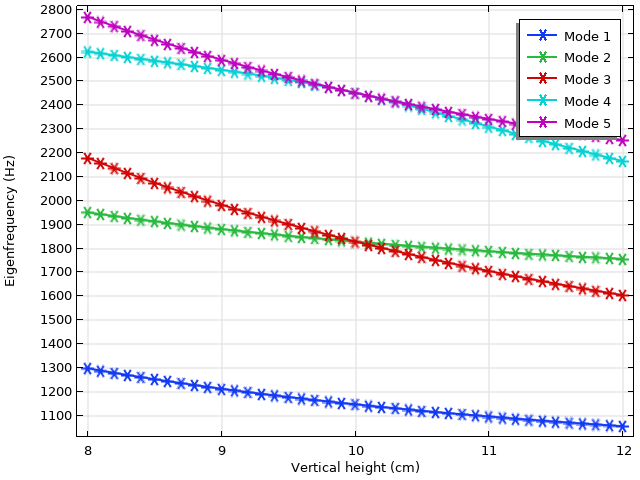
Les fréquences propres des cinq premiers modes sont tracées en fonction du demi-axe vertical du domaine elliptique. Notez les dégénérescences entre les modes 2 et 3, ainsi qu’entre les modes 4 et 5, lorsque le demi-axe vertical est égal à 10 cm et que le domaine est parfaitement circulaire.
Les fréquences propres des cinq premiers modes sont tracées ci-dessus. Notez que lorsque le demi-axe vertical est de 10 cm, le domaine modélisé est parfaitement circulaire. Cela entraîne des dégénérescences entre les modes 2 et 3, ainsi qu’entre les modes 4 et 5. En fait, au-delà du point dégénéré, l’ordre des modes 2 et 3 s’inverse sur le graphique de valeurs propres. Ce type de comportement de croisement de mode est courant dans de nombreuses études de fréquences propres. Comment suivons-nous ces modes sur un graphique de valeurs propres lorsque leur ordre a été mélangé? Pour répondre à cette question, observons de plus près l’un de ces modes.
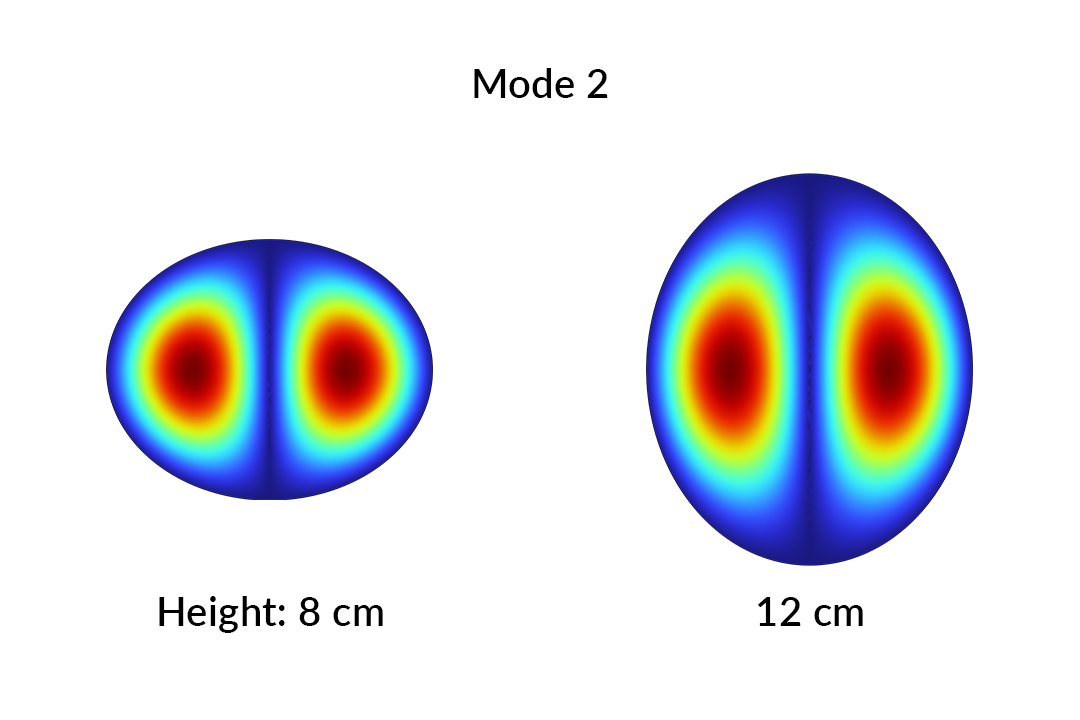
Le mode 2 est affiché pour les deux extrémités de la plage du paramètre.
Le mode 2 est affiché ci-dessus lorsque le demi-axe est de 8 cm, et lorsqu’il est de 12 cm. Pour l’oeil humain, la ressemblance entre ces deux modes est évidente. Nous pouvons quantifier cette ressemblance avec l’intégrale de recouvrement des modes:
Les variables u_i et u_j représentent deux solutions arbitraires de modes propres. La partie clé de cette équation se trouve dans le numérateur: nous réalisons un produit scalaire entre les deux modes. Le dénominateur normalise la valeur de ce recouvrement M de façon à ce qu’il soit compris entre 0 et 1.
Le recouvrement d’un mode avec lui-même est 1. Le recouvrement entre deux modes distincts pour une même valeur de paramètre est 0, étant donné qu’ils sont orthogonaux. Pour des modes avec différentes valeurs de paramètres, M sera proche de 1 si les modes ont une ressemblance qualitative. Par exemple, les deux modes ci-dessus ont une valeur de recouvrement M = 0.95, confirmant notre identification visuelle. Deux modes différents auront une valeur de recouvrement proche de 0.
Avec cette mesure, nous pouvons mettre en place une stratégie de correspondance de modes en imposant un certain seuil sur la valeur de recouvrement. Cela peut être utilisé pour filtrer ou regrouper des modes dans des diagrammes de dispersion et même pour générer automatiquement des animations de profil de mode à l’aide d’une méthode de modèle. Dans les sections suivantes de cet article de blog, regardons comment mettre en oeuvre cette stratégie à des applications à différentes disciplines physiques.
Exemple 1: Guide d’ondes optiquement anisotrope
Dans un article de blog précédent sur la modélisation de milieux optiques anisotropes, nous avons regardé les modes transverses d’un guide d’ondes optiquement anisotrope. Ces modes peuvent être regroupés par la direction prédominante du champ électrique, ainsi que par le nombre de maximums de l’amplitude dans le plan transverse. Un échantillonnage des modes E^x_{ij} est montré ci-dessous.
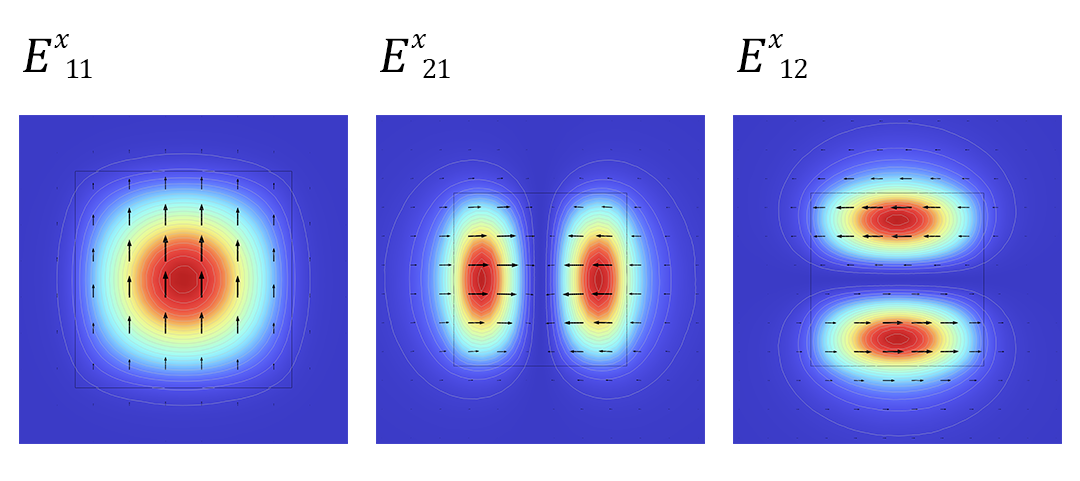
Les trois premiers modes propres E^x_{ij} dans un guide d’ondes optiquement anisotrope.
Etant donné que l’objectif premier d’un guide d’onde est de contrôler le flux lumineux, il est crucial de comprendre le comportement de ces modes de propagation. A chaque fréquence, chaque mode a un indice de réfraction effectif associé qui détermine à quelle vitesse ils se propagent, leur longueur d’onde effective et quelle est l’intensité de leur atténuation (s’il y a des pertes dans le modèle). Nous utilisons un diagramme de dispersion pour visualiser comment l’indice de réfraction effectif varie en fonction de la fréquence.
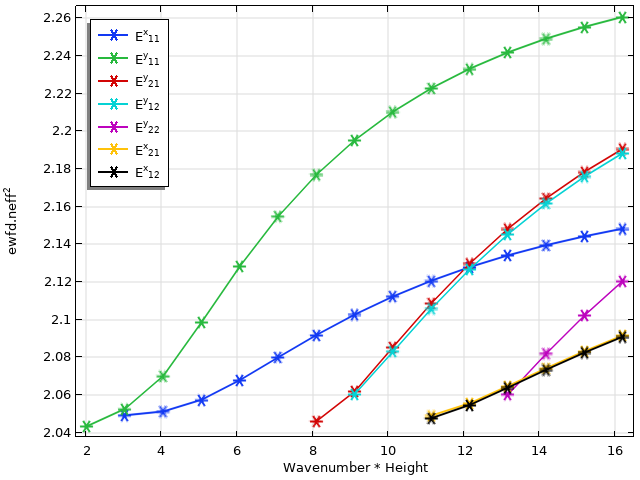
Le diagramme de dispersion du guide d’onde est affiché ci-dessus. Les nombreux croisements de modes rendent nécessaire la catégorisation des modes propres de façon à les étiqueter correctement.
Dans les résultats bruts de l’étude d’analyse de mode, les indices de réfraction effectifs ne sont ni groupés ni ordonnés d’aucune façon étant donné que le solveur ne connait pas ces modes a priori. Nous appliquons le calcul de l’intégrale de recouvrement pour classer ces valeurs propres par profil de mode. Etant donné que chaque valeur d’indice de réfraction est désormais associée à un mode spécifique E^x_{ij} ou E^y_{ij}, nous pouvons facilement utiliser des filtres et des options d’affichage pour colorer et annoter chaque mode dans la légende du graphique. Notez que cette méthode permet de résoudre correctement de multiples croisements de modes, ainsi que des modes avec des valeurs propres très proches, tels qu’entre les modes E^{x,y}_{12} et E^{x,y}_{21}.
Exemple 2: Fréquences propres d’une pale en rotation
Comprendre les modes de résonance d’un composant en rotation, tel qu’une pale d’éolienne ou un moteur de voiture électrique, est d’une importance critique pour des applications comme l’analyse de stabilité ou la minimisation du bruit et des vibrations. Intéressons-nous à l’exemple simple du modèle Fundamental Eigenfrequency of a Rotating Blade de la Bibliothèque d’applications.
La pale rectangulaire étant mise en rotation à des vitesses angulaires de plus en plus élevées, nous nous attendons à ce que deux phénomènes majeurs et en opposition dominent: la précontrainte et l’assouplissement centrifuge. Le premier rigidifie la pale en raison du champ de contraintes statique de l’effet centrifuge et se traduit par une influence à la hausse de la fréquence propre. Le dernier assouplit la pale en raison de l’amplification radiale du mouvement, conduisant à une influence à la baisse de la fréquence propre. L’équilibre entre ces deux effets est mieux illustré dans un diagramme de Campbell, qui représente les fréquences propres en fonction de la vitesse angulaire de rotation.
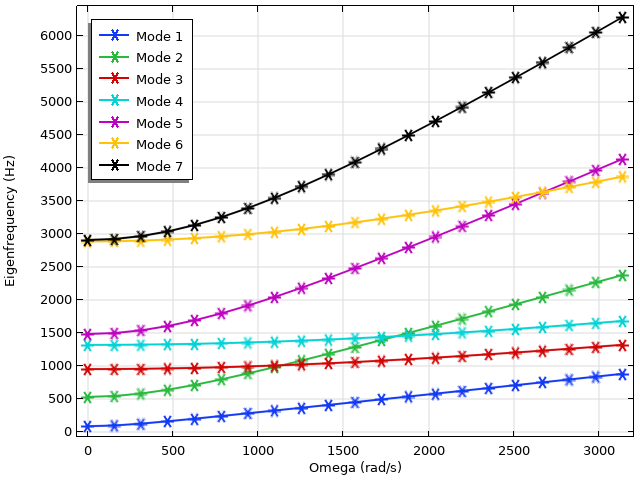
Diagramme de Campbell d’une pale en rotation. Notez l’augmentation significative des fréquences propres des modes 2 et 5.
Le diagramme de Campbell pour les sept premiers modes propres est affiché ci-dessus. En général, on observe une tendance à la hausse des fréquences propres, ce qui indique que la précontrainte a un rôle prédominant. C’est encore plus prononcé pour les modes 2 et 5, dont les valeurs propres augmentent de façon notable et croisent d’autres modes obtenus sur la plage de paramètre étudiée. Les déplacements et les contraintes des six premiers modes sont affichés ci-dessous.
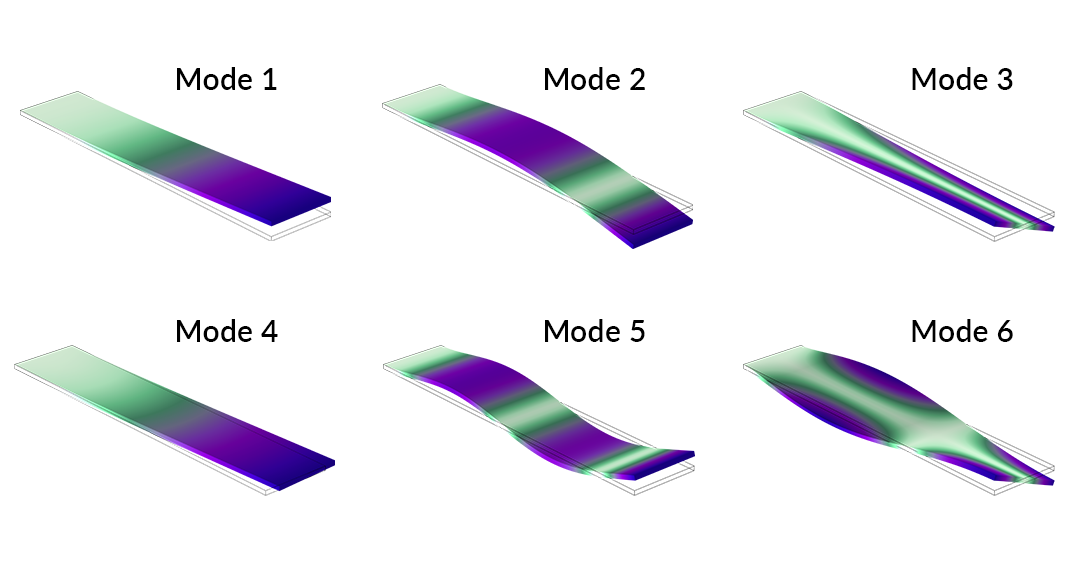
Les six premiers modes propres d’une pale en rotation.
Dans un système plus complexe, le diagramme de Campbell peut contenir davantage de fréquences propres présentant à la fois des tendances croissantes et décroissantes. Comprendre et visualiser ces tendances est important, par exemple, pour déterminer les vitesses critiques. L’intégrale de recouvrement de modes permet de classer ces familles de modes et de suivre facilement leur comportement.
Exemple 3: Modes propres dans un silencieux avec des parois élastiques
La simulation multiphysique joue un rôle clé dans la conception de silencieux pour les moteurs à combustion interne. En plus de modéliser les ondes de pression dans la masse d’air, il est également nécessaire de prendre en compte l’interaction de la masse d’air avec l’enceinte du silencieux. Cela permet d’obtenir un profil de transmission plus précis sur la plage fréquentielle.
L’un des effets de l’interaction acoustique-structure est l’introduction d’un nombre beaucoup plus important de modes de résonance, comme on peut le voir dans ces exemples: Eigenmodes in a Muffler et Eigenmodes in a Muffler with Elastic Walls. Regardons de plus près le dernier modèle. Nous réalisons une analyse de mode de la section du silencieux sur une plage de fréquences de façon à déterminer les profils des modes et leurs fréquences de coupure correspondantes.
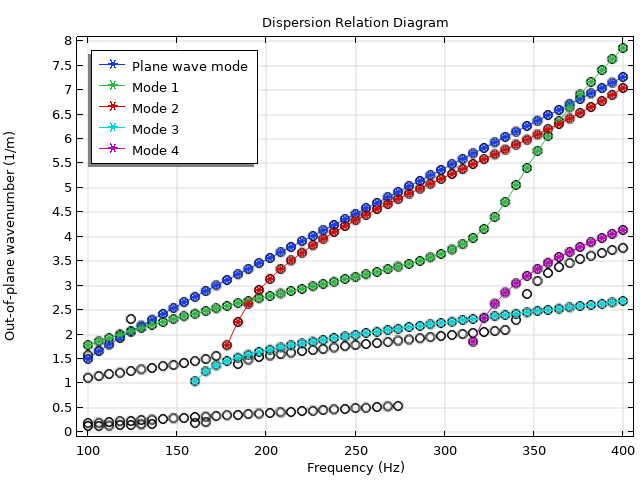
Diagramme de dispersion du silencieux avec parois élastiques. En plus du mode d’onde plane (bleu), notez la présence d’un nombre beaucoup plus important de modes dus à l’interaction acoustique-structure entre la masse d’air et les parois du silencieux. Un sous-ensemble d’entre eux est suivi en utilisant la méthode de recouvrement de modes.
Une sélection de modes et leurs constantes de propagation sont tracées en fonction de la fréquence dans le diagramme de dispersion ci-dessus. Il y a clairement des tendances dans le jeu de données qui semblent correspondre à des familles de modes distincts. Par exemple, le mode d’onde plane forme une ligne droite diagonale qui traverse l’ensemble de la plage de fréquences. En appliquant l’intégrale de recouvrement, on peut confirmer le comportement attendu de ce mode d’onde plane, et suivre plusieurs autres modes sur la plage fréquentielle. Ces profils de modes sont affichés ci-dessous.
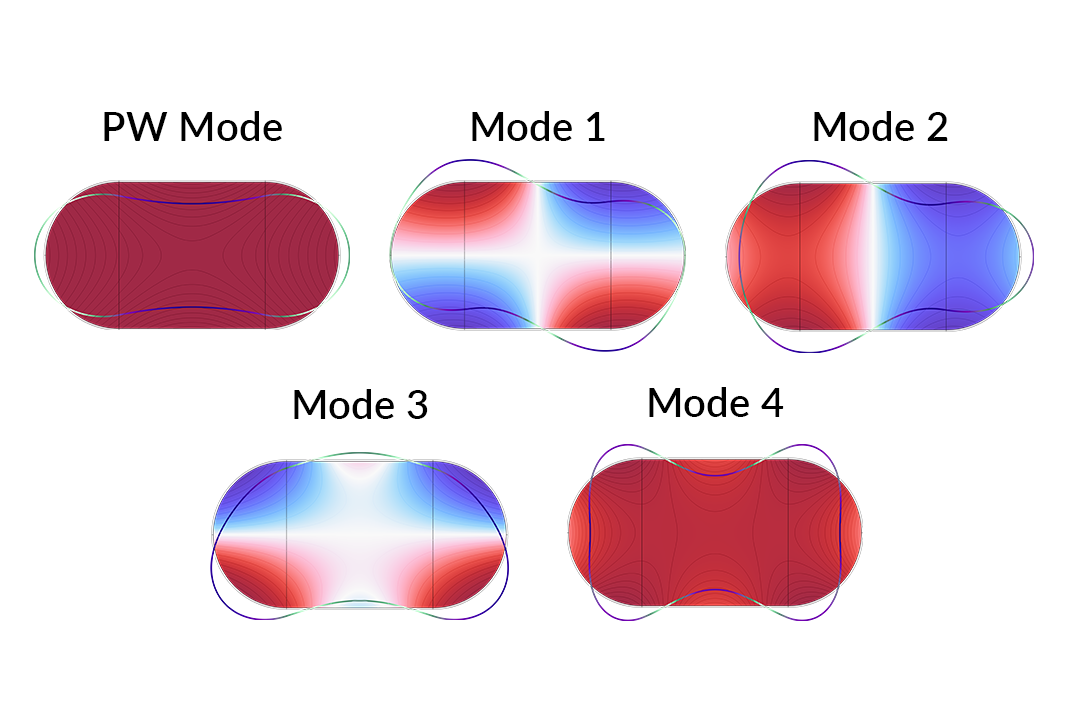
Une sélection de profils de modes dans le silencieux avec parois élastiques est représentée ci-dessus.
En utilisant une méthode de modèle, nous pouvons même générer automatiquement une animation montrant l’évolution du mode sur la plage de fréquences.
Une animation générée à l’aide d’une méthode de modèle, montrant l’évolution du mode 3 suivi sur la plage de fréquences.
L’animation ci-dessus montre l’évolution considérable du mode 3 entre 160 Hz (proche de sa fréquence de coupure) et 400Hz (limite haute de l’étude), en croisant de nombreux autres modes propres en chemin. Suivre l’évolution des familles de modes individuels devient plus facile avec l’intégrale de recouvrement de modes.
Prochaines étapes
Dans cet article de blog, nous avons montré l’utilisation de l’intégrale de recouvrement de modes pour suivre et catégoriser les modes dans des études de fréquences propres. Pour vous lancer, cliquez sur le bouton ci-dessous, qui vous mènera à l’article du Centre d’apprentissage:
Par ailleurs, les modèles évoqués dans cet article de blog peuvent être téléchargés dans la Bibliothèque d’applications:
- Optically Anisotropic Waveguide
- Fundamental Frequency of a Rotating Blade
- Eigenmodes in a Muffler with Elastic Walls







Commentaires (0)