Articles techniques et présentations

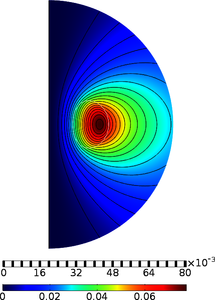
This talk is for users of the COMSOL Multiphysics® software who, like the present author, are relative newcomers to numerical simulation but have a strong grounding in Hydrodynamics or related areas of Mathematical Physics. As part of a multi-year plan to develop proficiency in Equation Based Modeling the present author has developed a sequence of COMSOL® simulations, each of which incorporates some complication that its predecessors did not. Simulations reported in prior COMSOL Conferences have addressed the complications presented by unbounded domains, presence of concentrated vorticity, and domains with double connectedness. The classical vortex ring is a flow that exhibits all three of these complications. The author’s earlier work on the vortex ring (reported in his paper in the Proceedings of COMSOL 2017) was only partly successful, owing to its restriction to an idealized vortex ring, a typical meridional section of which has a core in the form of a circular disk. This restriction led to the presence of a discontinuity in the component of velocity tangent to the core boundary—i.e. a slip velocity—that separates the rotational flow in the core from the irrotational flow outside it. If the flow is steady in time as seen by an observer moving with the ring—as assumed here—such a slip velocity is incompatible with continuity of pressure across the core boundary. The present work addresses this deficiency by allowing for a noncircular cross section of the core boundary. The family of noncircular cross sections incorporates two constraints a-priori, namely constancy of cross sectional area of the core and constancy of the centroidal radius, i.e. the transverse distance from the axis of symmetry to the centroid of the cross section. The boundary of the core cross section is represented in local polar coordinates in which the local radius (constant for a circular cross section) is replaced by a Fourier cosine series with respect to local polar angle (defined to be zero at the outer equator). The simulation employs Physics Interfaces of General Form PDE type in three distinct domains, an Interface of Weak Form Boundary PDE type on one boundary, and an Interface of Optimization type in one Component. In the Optimization the Object Function is the integral with respect to local arc length around the core boundary of the square of the slip velocity and the Control Variables are the coefficients of the aforementioned Fourier series. By incorporating twelve terms in the series the optimization reduces the Object Function to less than 0.001 times its value in the case when the core boundary has circular cross section and the maximum slip velocity to less than 3.2% of the mean of the tangential velocities on the two sides.