- Bridging the Terahertz Gap
- Modeling the Lithium-Ion Battery
- Protection contre la Corrosion
- Modélisation des batteries
- Modélisation et Simulation dans le développement des piles à combustible
- Modélisation thermique des petits satellites
- Analyse électro-vibroacoustique d'un transducteur à armature équilibrée
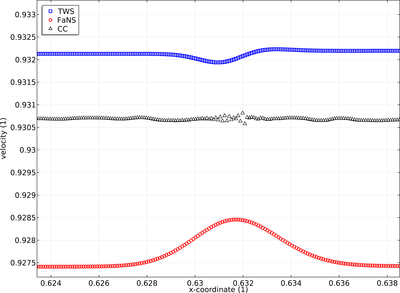
Investigation of 1D Compressible Navier Stokes Using Equation-Based Modeling
A fundamentally important area of the COMSOL Multiphysics® code is that of equation-based modeling. This root capability is unique in commercially-available codes and offers unlimited application. One specific area that requires more detail, even in the CFD Module of COMSOL®, is that of 1D Compressible Navier Stokes (NS) equations. The stabilization methods developed and demonstrated in 1D, can then be utilized in both 2D and 3D in a confident manner. Over 28 years ago, these equations were investigated, and also extended to 2D [1]. The methods developed therein have been significantly improved, as will be published in an upcoming monograph [2]. The advancements discussed are primarily concerned with the method of stabilization. Equations as input into the COMSOL® general form PDE in non-dimensional weak form are discussed and presented. Both the Taylor Weak Statement (TWS)[1] and Truncation Discretization Error Annihilation (TDE)[2] are implemented for 1D compressible NS equations. Results for Burger's Equation and Riemann Shock Tube benchmarks are compared directly between the TWS and TDE methods. A 2D approximation is implemented for the shock tube problem using the COMSOL® CFD Module high Mach number, Laminar Flow physics interface. Within this dimensional-form model, the COMSOL-consistent stabilization method is compared to TWS and TDE. If time allows prior to the conference start, a 2D Sajben nozzle benchmark problem could also be compared to TWS and TDE. An ultimate goal of this work is to incorporate the TDE stabilization method as an option for the CFD Module.