Improving RRAM performance through uncertainty quantification
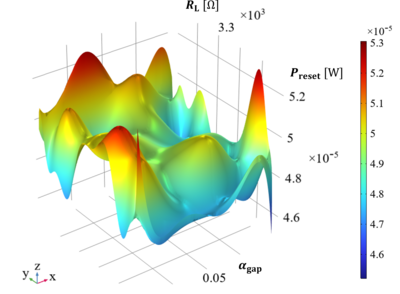
Resistive random access Memory (RRAM) is a non-volatile memory that operates by switching resistance between the formation (ON) and the rupture (OFF) of the conductive filaments (CF), representing the binary states of logic "0" and "1". RRAM is considered one of the most promising candidates for next-generation memory due to its attractive characteristics such as high memory density, fast write-read speed, low power consumption, and strong scalability. However, the uncertainty of the microstructure of the materials presents a significant challenge in further improving RRAM device performance. Therefore, employing uncertainty quantification (UQ) methods to investigate the influence of material factors on RRAM device performance becomes essential. The UQ module in COMSOL Multiphysics is an ideal platform for this purpose, as COMSOL seamlessly integrates modeling, simulation, and uncertainty quantification analysis within a single, cohesive environment. Based on the TiN/Hf/HfO2x/TiN RRAM model proposed by Niraula et al. [1], this work is focusing on two key performance indicators (KPIs) for RRAM devices: the on/off ratio and power consumption. The model consists of four modules corresponding to ON and OFF states and SET (OFF→ON) and RESET (ON→OFF) switching process, and each module is individually constructed in the COMSOL Multiphysics modeling software package. To integrate these modules seamlessly and extract KPIs, MATLAB is used, which communicates with COMSOL via the LiveLink for MATLAB. The four modules are programmatically linked together in MATLAB, and data are further processed to obtain the two KPIs. These KPIs are set as the output of MATLAB functions, which encapsulate modules that consist a specific process from model inputs to KPI outputs. To integrate KPIs into UQ analysis, corresponding MATLAB functions are created within the COMSOL Desktop, serving as the quantity of interests. To ensure the MATLAB functions can be called correctly, the connection between COMSOL and MATLAB is manually established via the COMSOL server. Subsequently, UQ is employed to conduct screening, sensitivity analysis, uncertainty propagation, and reliability analysis. Finally, the optimization module in COMSOL provides the optimal parameter combinations for maximizing the model's performance. The UQ analyses not only reveal how material parameters impact performance, but also predict the probabilistic distribution relationship between parameters and device performance. In addition, a theoretical 13-fold enhancement in the on/off ratio is achievable by reducing the thickness of the HfO2 layer (h) to 3nm and increasing the conductivity of CF (σCF) to 10^5 S/m. However, the reliability analysis reveals that the probability of attaining such a significant on/off ratio is extremely low. On the other hand, by adjusting h to 9 nm, increasing σCF to 10^5 S/m, and setting the SiO2 thermal conductivity at 1.5 W/(m·K), the SET power consumption is significantly reduced by 32%, and the reliability analysis indicates a probability of 0.158 for achieving this improvement. Moreover, when h is thinned to 3 nm, σCF is increased to 10^5 S/m, and the load resistance is adjusted to 3.5 kΩ, the RESET power consumption drops by 38%, and the reliability analysis reveals a probability of 0.186 for the optimizations. These results demonstrate a notable reduction in both SET and RESET power consumption and indicates a more practical level of performance enhancement. The uncertainty relationship between microstructure and parameters is currently under investigation and will be presented in future work.