Growth of Transient Quantum Mechanical Dirac Wave Functions Through Electric or Magnetic Fields
INTRODUCTION: The Dirac equation is employed in particle physics and historically gave the first combined unification of quantum mechanics and relativity theory by introducing a four component wave function Ψn n=1…4. This wave function describes the behavior of fermion type particles (e.g. electrons). The effect of a pre-existing magnetic vector potential {A} and/or a scalar electric potential Φ on the classical Dirac equations are treated by adding additional terms in the free field PDE’s [1]. COMSOL Multiphysics® simulation software is used for obtaining a simpler 2-D wave function [Ψ1(x,y,t),Ψ4(x,y,t) ] as a solution to the coupled time dependent Dirac equation where dependent variables vary with time. The probability density ρ(x,y,t) = |Ψ1|^2 + |Ψ4|^2 of a particle being at a spacial point is treated with the "wave function formulation" which involves solving the electromagnetic Dirac field PDE's for Ψn .
USE OF COMSOL MULTIPHYSICS®: The General-Form PDE "time dependent" study is employed. When the wave vector k lies in the xy plane, the 4 component Ψn uncouples into two PDE’s in terms of components for n=1&4. PW waveguide examples are solved to test COMSOL’s Dirac transient solving capabilities (in the presence of a {A} or Φ potential) as validated (when possible) against alternate FEM or exact solutions.
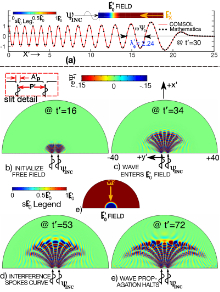
RESULTS: PW Wave guide Models: The wave guide Plane Wave solution, illustrated by the 2-D finite bar (Fig.(1A) inset), having an electric field vector Ex, which is bounded by an electric free zone at the start of the model. The front end is driven with ΨnoExp(-iωt) and solutions are terminated before propagating waves reach the outer boundary. The Ψ1(x,t) wave propagation (with gradually decreasing spatial frequency and growing amplitude) is shown in Fig.(1A), illustrating a validation of the COMSOL FEM vs Mathematica FEM solution. Similar results are also presented for cylindrical waves through an Ex field.
Two Slit Models: Via two slits, an incident PW enters an infinite domain having a pre-existing in plane Electric field vector Ex, which is bounded by a radial electric free zone at the Fig.(1F) start of the model. In Figs.(1B-E), waves emerging from the slits interact, forming bands of constructive and destructive interference in a curved blade like pattern as opposed to the no Ex field straight blade shaped pattern.
Similar bar and 2-slit models are solved, with results presented for wave functions passing through Bz magnetic fields.
CONCLUSION: Agreement between the alternative FEM solution validations were good. The effect of the magnetic or electric field on solutions resulted in wave functions having gradually varying spatial frequencies and amplitude shapes for Ψ1(x,y,t),Ψ4(x,y,t) and hence the probability distribution ρ(x,y) .
REFERENCES:
[1] Paul Strange, Relativistic Quantum Mechanics, Cambridge University Press Cambridge
UK, 1998.
Figure 1 (A) PW Wave Function Ψ1(x) in Ex Electric Field (−−FEM COMSOL vs ••• FEM Mathematica); (B➛E) Ψ1(x,y) thru Two Slit Ex Electric field @ 4 sequential time snapshots ; (F) Ex field distribution
Téléchargement
- kalinowski_poster.pdf - 10.38MB
- kalinowski_paper.pdf - 16.46MB
