Coupling the domains structure and Tensor Magnetic Phases with AC/DC fields in soft magnetic materials
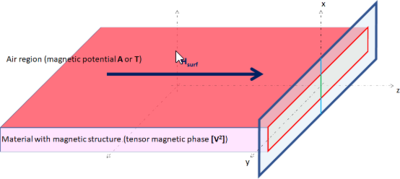
Local and microscopic non-uniformities within the magnetic structure (domains and walls [1]), mainly due to surface effects, anisotropy and exchange energies [2, 3], express itself with space variations of domains geometry and properties from the bulk towards the surface. A first work [5] proposed to cope with the problem of soft magnetic materials heterogeneity in terms of domains structure at a static equilibrium. For this purpose, it is proposed to describe a magnetic structure from a mesoscopic point of view thanks to one tensor variable [Lambda²], statistically gathering main topological and dynamic properties of the magnetic domains and walls [5, 7]. Typical subdivisions were introduced by defining a tensor state variable [V²]=[Lambda²]^-1 with 6 unknowns. In reference [6], a way is initiated to couple static and dynamic relationships between the magnetic field and the magnetic polarization to domains and walls structuring. The latter method, called the Tensor Magnetic Phase theory (TMP) [8], is supposed to provide a deterministic method that predicts the geometry dependent vector behavior, including static and dynamic hysteresis and iron losses, of every soft materials. The material structuring can be explained thanks to energy tendencies, for a given value of the tensor components of [Lambda²]0=[Lambda²]surf at the surface of a sample. Therefore, in addition to a material parameter K, related to a ratio between the total anisotropy (magneto-crystalline or induced by magnetostriction and stress) and the exchange energy density of walls, and a volume diffusion time constant Tau; it is necessary to know the surface magnetic properties of the material, i.e. the walls surface, density and mobility, including the closure domains. The main challenge is thus to be able to infer these latter properties from boundary conditions that can be calculated through classical formulations in neighboring regions (magnetic vector A or electric vector T potential, i.e. induction B or field H) and identified material properties (induction-field static and dynamic relationship). We investigate a way to make a link/coupling between the classical state variables used in electromagnetic FEM formulations (A and B or T and H) and the tensor state variable ([V²]0=[V²]surf) through first an energy balance and secondly the fields’ boundary conditions, taking the dynamic magnetic behavior [4] into account, at the surface of the material. The aim of this paper is to define, implement and put to the test (Figure 1) the physical equations that should be used in the bulk and at the surface of a soft magnetic material to make an efficient coupling between classical formulations used in electromagnetism for non-magnetic materials and the Tensor Magnetic Phase formulation proposed by [8] inside the magnetic material. Adequate boundary conditions for the Tensor state variable [V2]surf and the magnetic induction B and applied field H will be derived first from a surface energy balance and secondly from the boundary conditions on B and H, taking the dynamic magnetic behavior of the material into account, expressed thanks to either a weak formulation or an Ordinary Differential Equation (ODE). This model provides a way to either identify or analyze and quantify the impact of a surface magnetic structure modification induced by various treatments (irradiation, scribing, ablation …) onto the volume magnetic structure and consequently onto the global magnetic behavior.
In this work we propose to: - Sum up the basic principles of the TMP theory - Introduce the two main coupling equations to be implemented at borders o Coupled Degrees of Freedom (6+3=9 DoF): [V²]surf and B=rot(A) or H=T o Surface governing equations on [V²]surf and weak formulation on the surface o Boundary field B and H conditions and magnetic dynamic behavioral equation o Discussions: Contribution of the Zeeman energy on the surface ? In the volume ? - Develop and Implement the formulation for a 1D test case with Non Grain Oriented (NGO) and Grain Oriented (GO) materials. Analysis inside the thickness e of V² (Figure 2) of an electrical steel sheet submitted to a uniform magnetic field applied Hsurf=H(x=+-e/2) at the surface along the z axis (Figure 2). o Definition of the 1D Test case (4 DoF for GO and 7 DoF for NGO) o Magneto-harmonic solution(s) (Lambda² and B(x)) o Discussions: Description of main domains (space variations and refinement), closure domains (orientation and space variations) and magnetic polarization. - Investigate the coupling formulation for a 2D test case with NGO and GO materials Analysis inside the cross section V² (Figure 3) of an electrical steel sheet submitted to a uniform magnetic field applied Hsurf at the surface along the z axis.