- Bridging the Terahertz Gap
- Modeling the Lithium-Ion Battery
- Protection contre la Corrosion
- Modélisation des batteries
- Modélisation et Simulation dans le développement des piles à combustible
- Modélisation thermique des petits satellites
- Analyse électro-vibroacoustique d'un transducteur à armature équilibrée
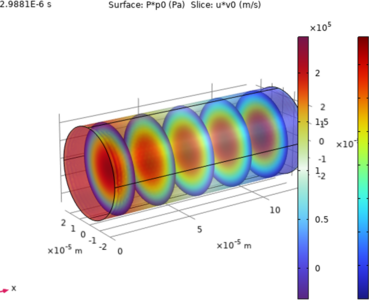
Compressible Fluid Flow Modelling in COMSOL
COMSOL offers three different fluid flow models: (1) Incompressible fluid (2) Weakly compressible fluid and (3) Compressible fluid with low Mach numbers (<0.3). In the case of compressible fluid, the continuity equation is modified to include the time-dependent density variation caused by external factors such as temperature. However, in some applications, it is often needed to solve for the time-dependent pressure variation caused by the compressibility of the fluid. At present, there is no pre-built Physics interface available in COMSOL for this case. In this paper, we report some results of our custom implementation of this aspect of the compressible fluid flow using COMSOL Mathematics interface. This is done by replacing the continuity equation with the following equation for the time dependent pressure. dP/dt=ρc^2 (∇.u) (1) where rho is the density of the fluid (assumed to be constant), c is the velocity of sound in the fluid and u is the fluid velocity vector. The term rho*c2 on the right-hand side of eq.1 is the bulk compressibility of the fluid. Eq. 1 relates the imbalance of fluid flow in a small control-volume to the time dependent pressure variation within that microscopic volume. In this work, we have implemented Eq.1 along with the standard Navier Stokes equation for momentum conservation using the coefficient form partial differential equation (PDE) in the Mathematics interface in COMSOL ver. 6.2 along with the add-on CFD Module. Two different studies were included in the same model. (1) Using the standard incompressible Laminar Flow Physics interface in the CFD module. (2) Using the coefficient form of the PDE in the Mathematics interface in which both the Navier Stokes equation and the modified continuity eq. 1 were cast in the form of Standard Coefficient form PDE. Results of our simulation from these two studies are compared. Velocity and pressure distribution along the flow direction show the expected differences between the two studies, as shown in Figs. 1 -3. Helmholtz oscillations are also seen in the compressible flow model when a sudden pressure pulse is applied, as shown in Fig. 4. We find that such compressible fluid flow models are necessary for modelling piezo-inkjet systems for high viscosity inks.