A Multiscale Approach to Simulate Vacuum Drying of a Packed Bed of Spray-Frozen Particles
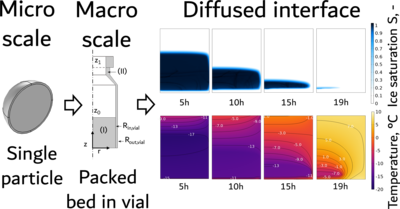
Preservation of biopharmaceuticals by spray freeze-drying is of great interest as it involves gentle drying and can be easily integrated with continuous manufacturing strategies. The drying of packed beds have been extensively studied experimentally, but a detailed mathematical model of such systems is still missing. The intrinsic multiscale nature of the phenomenon, i.e. drying of porous particles randomly stacked in porous beds, poses a number of challenges that previous studies failed to address. The objective of this work is to present the implementation on COMSOL Multiphysics® of a new model, describing the drying of packed beds of frozen particles through the concept of a diffused interface. The simulations of a single particle at the micro-scale are used to inform the model of the packed bed at the macro-scale. The specific example of the drying of particles in a vial was used as a case study. The macroscopic domain, composed of the glass vial and the packed bed, was constructed as a 2D axisymmetric geometry. The Heat Transfer in Porous Media and Transport of Diluted Species in Porous Media interfaces were used to solve the heat and mass transport equations in the packed bed, while only the heat transfer was considered for the glass domain. In the packed bed, the Dusty-Gas Model (DGM) was implemented defining the diffusion and the convection terms in the pre-built transport equations. An additional Species source was added in the bed volume to account for the ice sublimation (or condensation) from the particles. This source term was determined based on the local fluid- and thermo-dynamics conditions and on the sublimation kinetic parameter, vs, which was determined from the simulations at the micro-scale. The sublimation thermal effect was accounted for adding a Heat source to the domain, calculated multiplying the aforementioned mass generation and the latent heat of sublimation. Finally, with the Domain ODEs and DAEs, the sublimation flux was integrated over time to obtain the sublimated ice and the local frozen fraction (S) of the bed. The diffused interface results from the distribution of the frozen fraction in the bed. At the micro-scale, a single particle was simulated to obtain vs. The particle was divided in two domains, i.e. dried and frozen layer, and the interface motion was determined solving the Stephan problem in the Deformed Geometry interface. In the dried layer, the vapor mass transport was solved using the Darcy’s law model. The kinetic parameter, vs, was determined integrating the sublimating mass flux over the interface surface and dividing the result by the driving force. Multiple simulations with different particle porosities were performed and the evolution of vs(S) was exported to the macroscopic simulation as interpolation functions. The results show that this model predicts well the drying behavior of packed beds of frozen particles, distinguishing between scenarios in which either the bed or the particles porosity limits the mass transport, and predicting the development of multiple diffused sublimation fronts, as was theorized in the past.