Certains problèmes de modélisation donnent lieu à des solutions particulièrement élégantes. Un tel cas s’est récemment présenté avec la recherche d’une solution stationnaire temporelle à un problème impliquant un circuit électrique non linéaire. Regardons plus attentivement cet exemple pour voir comment certaines fonctionnalités intégrées au logiciel aident à mettre en place une implémentation efficace.
Le scénario de modélisation : un transformateur non-linéaire
Dans un précédent article de blog “Utiliser l’inductance différentielle et les bobines dans COMSOL Multiphysics”, nous avons vu le cas d’un transformateur constitué de deux bobines enroulées autour d’un noyau de matériau magnétique non linéaire. Appliquer une tension alternative sinusoïdale induira des courants dans la bobine primaire et la bobine secondaire. Cependant, à des courants suffisamment élevés, la non linéarité du matériau affectera de façon significative les inductances différentielles, et les courants induits n’auront pas une forme sinusoïdale. Nous pouvons modéliser ce comportement en construisant soit un modèle complet du dispositif, soit un modèle équivalent du circuit électrique où les inductances différentielles non linéaires sont prises en compte. Les non linéarités conduisent à l’obtention de courants qui seront périodiques, bien que non-sinusoïdaux, dans le temps. Nous pouvons observer cette réponse graduelle en effectuant un calcul temporel sur plusieurs périodes.

Un transformateur consistant en deux bobines enroulées autour d’un noyau non linéaire. Les inductances différentielles peuvent être extraites d’un modèle par éléments finis et utilisées dans un modèle de circuit équivalent.

Les résultats obtenus après avoir lancé le calcul d’un modèle de circuit équivalent sur de nombreux cycles montrent que le régime permanent périodique en temps est progressivement atteint.
Les résultats montrent clairement qu’il sera nécessaire de simuler un nombre important de périodes, et si l’on est intéressé uniquement par le régime permanent périodique en temps, alors la plupart des données générées ne sont pas réellement nécessaires. Idéalement, dans ce cas de figure, nous voulons une méthode conduisant directement à cette solution périodique en temps, et c’est ce que nous allons voir maintenant.
Reformulation du circuit équivalent du domaine temporel au domaine spatial
Si nous regardons de plus près notre modèle de circuit électrique, nous constatons que celui-ci n’a que deux inconnues variant dans le temps: I_1 et I_2, le courant passant à travers les bobines primaire et secondaire. Passons maintenant au schéma du circuit, et étudions cela en termes de sauts de potentiel à travers chaque composant des deux boucles de courant :
où toutes les inductances différentielles sont fonction des deux courants: \partial L_{ij} (I_1,I_2). Cet ensemble d’équations différentielles ordinaires couplées peut être résolu de nombreuses façons. Nous nous limiterons au cas où la tension appliquée V_{AC} et la solution sont périodiques en temps sur une période donnée, appelée T_0.
Nous pouvons directement observer qu’il s’agit presque d’un ensemble d’équations algébriques non linéaires, à l’exception des dérivées temporelles des courants. Mais que se passe-t-il si l’on remplace ces dérivées temporelles par des dérivées spatiales ? Voyons ce que cela donne!
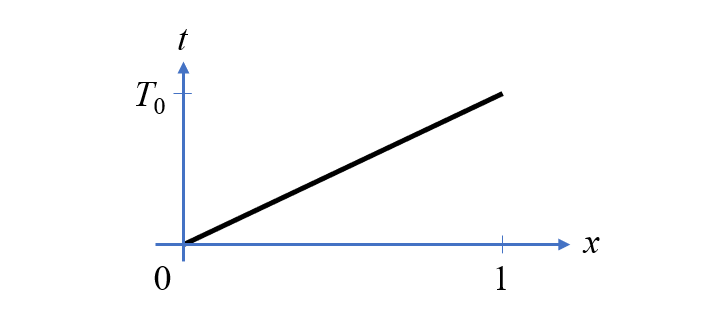
Temps en fonction de la position le long d’un domaine 1D de longueur unitaire.
Considérons un domaine 1D — un simple segment de longueur unitaire — sur lequel on définit une variable quasi-temporelle variant linéairement suivant la longueur. Si l’on définit deux grandeurs variant spatialement le long de cette ligne, u_1 et u_2, et que l’on maille cette ligne, alors le logiciel COMSOL Multiphysics® peut calculer la dérivée spatiale, \partial u_1 / \partial x, via l’opérateur différentiel: d(u1,x). Mais comme cette dimension spatiale représente ici la dimension temporelle, c’est en réalité une dérivée temporelle. Cela étant dit, nous pouvons désormais construire une équation algébrique de champ grâce à l’interface EDO et EAD sur domaine, définie sur un segment de longueur unitaire. Cette interface est visible dans l’image ci-dessous, où nos deux inconnues sont définies. Nous utiliserons des éléments Lagrangiens de façon à garantir une continuité des champs, et nous pouvons renseigner les unités appropriées pour chacun des champs et pour la source. Pour plus de lisibilité, nous pouvons également définir un ensemble de variables décrivant le saut de tension dû à tous les composants du circuit modélisé, comme mis en place dans les captures d’écrans ci-dessous.

Mise en place d’une interface EDO et EAD sur domaine, avec le nom attribué aux variables de champs, la fonction de forme sélectionnée et les unités renseignées.

Les variables définissant la tension appliquée dans le domaine spatio-temporel, la dérivée de chacun des courants, et le saut de tension le long des différents composants du circuit.
Ces variables sont utilisées au sein de la fonctionnalité Equation algébrique de l’interface EDO et EAD sur domaine, qui présente deux champs d’entrée pour une équation qui doit toujours être égale à zéro. Ici, nous renseignons la somme des sauts de potentiel, ainsi que la source, pour les deux boucles de courant. Ce sont les équations présentées précédemment. Enfin, deux conditions de Contraintes au niveau des points sont ajoutées à l’un des points situé à l’extrémité du domaine. La contrainte est basée ici sur un opérateur Intégration, défini sur l’autre extrémité. Les contraintes u1-intop1(u1) et u2-intop1(u2) assurent la condition de périodicité.

Mise en place de l’équation à satisfaire en tous points de l’espace-temps le long du domaine unitaire.

Définition d’une condition de périodicité grâce à la condition Contrainte au niveau des points et l’opérateur Intégration .
Résoudre ce problème stationnaire nécessitera un maillage relativement fin le long du domaine lorsque le dispositif fonctionnera dans le régime le moins linéaire. Ainsi, la taille des éléments du maillage le long de la ligne unitaire est le paramètre qui doit être étudié lorsque l’on résout ce modèle stationnaire non-linéaire. Les résultats sont représentés ci-dessous, et sont en accord avec ceux obtenus via l’étude temporelle. En effet, il est possible de réduire davantage l’écart en résolvant le modèle transitoire avec des tolérances plus strictes, ce qui aura pour conséquence d’augmenter le temps de calcul (de l’ordre de la minute pour un modèle petit comme celui-ci), alors que le problème stationnaire peut être résolu presque instantanément.

Comparaison entre les résultats obtenus via l’étude temporelle sur le modèle du circuit électrique et les résultats stationnaires obtenus avec l’approche périodique en temps.
La solution obtenue sur une période spatiale permet d’extraire le contenu fréquentiel via le jeu de données FFT spatiale. Les réglages de cette fonctionnalité sont visibles dans la capture d’écran ci-dessous, avec le jeu de données Tableau 1D mis en évidence. Ce dernier permet de reproduire périodiquement la solution spatio-temporelle, de façon à ce que les résultats apparaissent plus lisses. En affichant une quantité normalisée appropriée, nous observons comment le contenu fréquentiel augmente lorsque la tension appliquée augmente également.

Le jeu de données FFT spatiale prend en entrée le jeu de données Tableau 1D, qui reproduit les résultats stationnaires obtenus dans la direction temporelle.

Affichage du contenu fréquentiel lorsque la tension alternative augmente.
Conclusion
Dans cet article de blog, nous avons étudié une approche particulièrement intéressante permettant de résoudre le régime permanent d’un système périodique en temps pouvant être décrit par un ensemble d’équations algébriques. Notons que cette approche admet n’importe quel type de signal appliqué — pas uniquement des fonctions sinusoïdales — tant qu’il existe une solution périodique en temps lissée. Sa mise en place est relativement simple et tire avantage de fonctionnalités natives de COMSOL Multiphysics®, rendant cette approche utile pour tout type de problème, qui ne se restreignent pas à des circuits électriques. C’est une bonne technique que tout utilisateur de COMSOL peut avoir dans sa boîte à outils.
Le tutoriel utilisé dans cet article peut être téléchargé ici :




Commentaires (0)