Utiliser l’inductance différentielle et les bobines dans COMSOL Multiphysics^®

Lorsque l’on modélise un système électromagnétique à basse fréquence comprenant des bobines, des matériaux non linéaires, des aimants et des pièces mobiles, on est souvent intéressé par le calcul de l’inductance différentielle. Cette dernière quantifie les champs qui apparaissent dans ces systèmes électromagnétiques lorsque des courants variables dans le temps traversent l’une des bobines. Les inductances différentielles sont particulièrement utiles pour construire des modèles réduits simplifiés. Voyons ce qu’il en est, en théorie et en pratique, de l’utilisation de ces inductances différentielles dans le module AC/DC, un produit complémentaire du logiciel COMSOL Multiphysics^®.

Un bref rappel de la théorie

Le concept d’inductance est pertinent lorsqu’il existe une ou plusieurs boucles de fil le long desquelles le courant peut circuler. Ces boucles, ou bobines, peuvent être composées d’un ou de plusieurs tours de fil. Nous considérerons une source connectée à l’une des bobines que nous appellerons le primaire. Nous considérerons également une charge connectée aux autres bobines, appelées secondaires. Ces charges peuvent représenter une combinaison arbitraire d’autres appareils électriques.

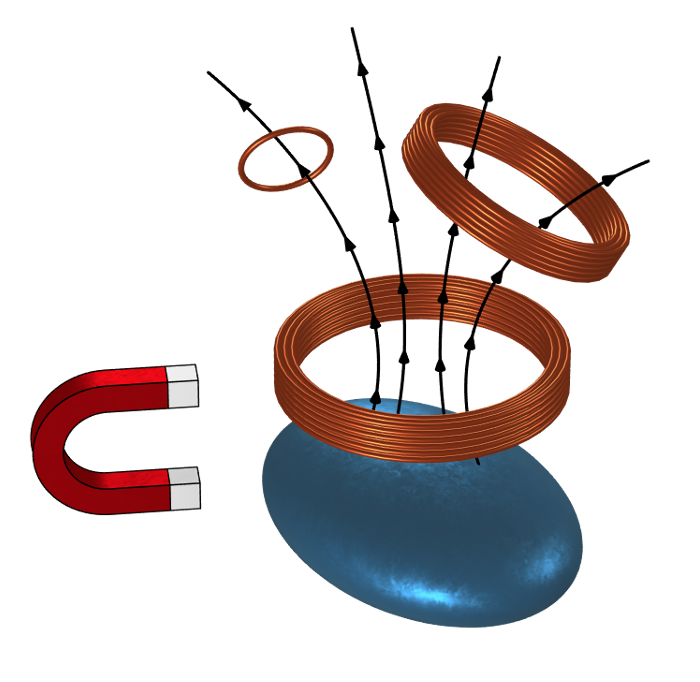
Plusieurs bobines dans l’espace, en présence de matériaux magnétiques non linéaires et d’aimants. Les courants variables dans le temps dans une bobine induisent des champs dans les autres bobines proportionnellement au flux intercepté, ce qui dépend de la façon dont les matériaux magnétiques non linéaires affectent ces champs.

Dans l’espace autour des bobines, il peut y avoir des matériaux magnétiques non linéaires et des aimants. Les matériaux magnétiques non linéaires peuvent évoluer dans leur régime non linéaire sous l’effet de l’aimant, du courant circulant dans l’une des bobines ou des deux. Chaque fois qu’un courant variable dans le temps est appliqué à la bobine primaire, une force électromotrice — une tension — est induite sur toutes les bobines, y compris la bobine primaire elle-même. Si les fréquences du signal appliqué sont bien inférieures à la fréquence de résonance du système, on peut se contenter de supposer que cette force électromotrice sera purement due au champ magnétique variable dans le temps. Dans cette hypothèse, la fonctionnalité Bobine est pertinente.

Pour un courant variable dans le temps circulant dans l’une des bobines d’indice i, la force électromotrice sur n’importe quelle bobine d’indice j est proportionnelle au taux de variation de la liaison de flux¹:

En appliquant le théorème de dérivation des fonctions composées et en supposant que \Phi est uniquement une fonction du courant instantané:

nous voyons que la tension induite est le produit de L’_{ij} , l’inductance différentielle par rapport au courant, et \dot{I_i}, le taux de variation du courant appliqué. Notons que si tous les matériaux du système sont linéaires, s’il n’y a pas d’aimants et si nous négligeons les pertes inductives dans les conducteurs, la relation devient:

 
où L_{ij} désigne l’inductance sécante, calculée par défaut dès lors que la fonctionnalité Bobine est utilisée. En revanche, le calcul de l’inductance différentielle nécessite quelques étapes supplémentaires.

Pour comprendre comment l’inductance différentielle est calculée, nous devons d’abord nous intéresser à la liaison de flux, qui est généralement décrite dans les manuels d’introduction à l’ingénierie comme l’intégrale de \mathbf{B}_i, le flux magnétique dû à l’excitation de la bobine i passant par la surface, S_j, délimitée par une fine boucle de fil représentant la bobine j:

Cependant, comme nous pouvons le voir sur l’image ci-dessus, la plupart des bobines ont une section transversale importante, de sorte qu’il n’est pas possible de définir simplement une surface, S_j. Au lieu de cela, nous appliquons le théorème de la divergence et utilisons le fait que \mathbf{B=\nabla \times A } pour calculer \Phi comme l’intégrale volumique du potentiel vecteur magnétique, \mathbf{ A }, projeté sur la direction selon laquelle le courant peut circuler dans la bobine, \mathbf{ J }:

Cette quantité est calculée automatiquement par le logiciel lorsqu’on utilise la fonctionnalité Bobine et est appelée flux concaténé de la bobine.

Ce flux concaténé peut être une fonction de différentes variables, bien que nous ayons supposé précédemment qu’il dépendait uniquement du courant instantané. Voyons maintenant comment calculer sa dérivée pour en extraire l’inductance différentielle.

Calculer l’inductance différentielle

Pour calculer l’inductance différentielle, nous devons évaluer la dérivée du flux concaténé dans toutes les bobines par rapport au courant appliqué dans le primaire. Cela peut être fait avec l’interface Sensibilité, que nous avons déjà abordée dans notre article de blog “Computing Design Sensitivities in COMSOL Multiphysics^®” et que nous allons brièvement passer en revue. Dans cette interface, il faut tout d’abord définir un Objectif global, dans lequel on saisit l’expression du flux concaténé de la bobine. Nous devons également définir au moins une Variable de contrôle global, utilisée pour calculer la dérivée de l’objectif. Ici, nous définissons une variable dont la valeur est multipliée par le courant continu circulant à travers le primaire. Dans cette configuration, l’étape Sensibilité peut être combinée à un Balayage de paramètres auxiliaires sur le courant appliqué, et l’inductance différentielle peut être calculée pour une plage de courants imposés.

Définition de la fonction objectif dans l’interface Sensibilité .

Définition de la variable de contrôle dans l’interface Sensibilité.

On utilise la variable de contrôle dans la fonctionnalité Bobine pour pouvoir dériver par rapport courant.

Balayage sur une plage de courants combiné à l’analyse de sensibilité.

Une fois l’étude résolue, vous pouvez créer une fonction de type Interpolation faisant référence à un Groupe d’évaluation afin que les résultats du calcul de l’inductance différentielle puissent être utilisés ailleurs dans le modèle.

Maintenant que nous avons à l’esprit les bases théoriques et méthodologiques, intéressons-nous à quelques exemples.

Un inducteur non linéaire

Pour commencer, nous modéliserons un noyau magnétique constitué d’un alliage de poudre de ferrite, un matériau magnétique non linéaire qui présente de très faibles pertes. Le noyau enveloppe une bobine, l’entourant à l’intérieur et à l’extérieur. Nous traiterons le modèle comme un modèle 2D axisymétrique. La bobine est composée de 80 tours de fil de 1 mm de diamètre et fonctionne à 50 Hz, de sorte que l’effet de peau est négligeable dans ces fils. La résistance en courant alternatif (AC) de la bobine peut donc être estimée de façon relativement précise à l’aide de la résistance en courant continu (DC). Dans ce cas, nous pouvons utiliser l’option Multispires homogénéisé de la fonctionnalité Bobine. Nous pouvons résoudre ce modèle dans le domaine temporel et obtenir le courant non sinusoïdal à travers l’inducteur en réponse à l’application d’une tension sinusoïdale.

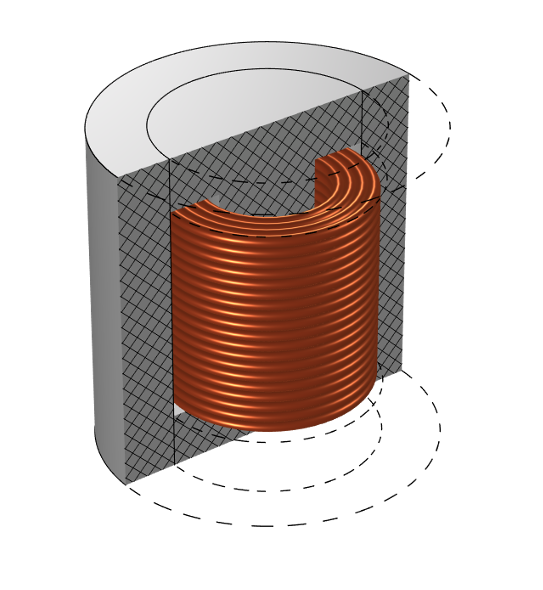
Un inducteur composé d’une bobine autour d’un noyau non linéaire BH.

Nous résolvons d’abord ce modèle pour une plage de courants DC afin d’obtenir l’inductance différentielle, comme indiqué ci-dessous, ainsi que l’inductance sécante à des fins de comparaison.

Inductances différentielle et sécante de l’inducteur constitué d’un matériau de noyau magnétique non linéaire sur une plage de courants DC imposés.

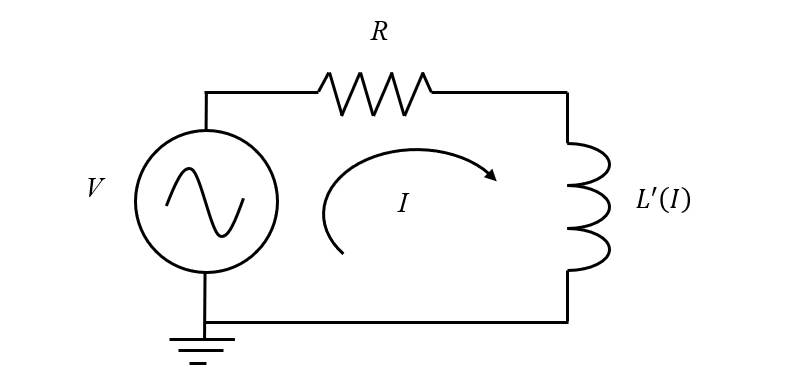
Le modèle de circuit électrique équivalent de l’inducteur non linéaire avec l’inductance différentielle qui dépend du courant.

Maintenant que nous disposons de cette inductance différentielle, nous pouvons l’utiliser dans un modèle de circuit électrique pour prédire rapidement le comportement transitoire. Notre modèle de circuit électrique n’a besoin que de trois fonctionnalités, en plus de la fonctionnalité Noeud à la masse ajoutée par défaut:

• Une Résistance
• Un Inducteur
• Une Source de tension

Nous utilisons une Résistance dont la valeur est égale à la résistance calculée de la Bobine. Nous ajoutons en série un Inducteur caractérisé par une inductance non linéaire définie via la fonction de type Interpolation qui stocke l’inductance différentielle calculée précédemment. Cette inductance non linéaire peut devenir une fonction de la valeur absolue du courant, puisque le comportement non linéaire ne dépend pas du signe du courant. Enfin, la Source de tension peut être placée en série. Ensemble, ces trois fonctionnalités permettent d’obtenir un modèle réduit prédictif. Les résultats de ce modèle réduit peuvent être comparés au modèle par éléments finis. Notez que sur les premières périodes, les modèles ne font que commencer à s’approcher de la réponse périodique en régime permanent de ce système non linéaire.

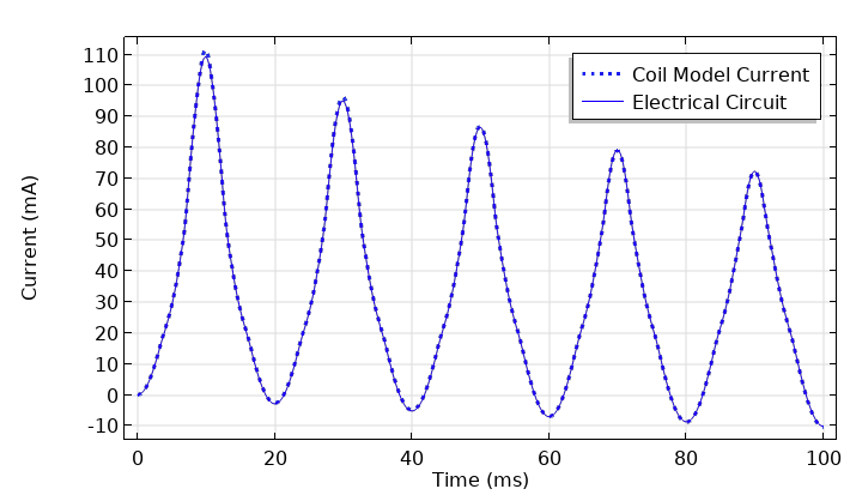
Graphique du courant à travers l’inducteur en présence d’une source de tension AC. Les résultats des modèles de circuit électrique et de champs magnétiques concordent.

Ces données temporelles peuvent également être converties dans le domaine fréquentiel grâce à la méthode de Fourier, afin d’identifier plus clairement les harmoniques supérieures introduites par la non-linéarité du matériau. Le modèle de circuit électrique étant rapide à résoudre, nous pouvons également examiner efficacement une large gamme de conditions de fonctionnement. Comme on pouvait s’y attendre, le contenu en hautes fréquences est plus important lorsque le dispositif entre dans le régime non linéaire.

Graphique du contenu fréquentiel du courant, pour une amplitude de tension croissante.

Un inducteur non linéaire polarisé par un aimant

À des fins d’illustration, nous allons maintenant modifier l’exemple ci-dessus en plaçant un aimant à côté du noyau. Cet aimant contribuera au flux concaténé de la bobine et polarisera le matériau non linéaire. L’inductance différentielle dépend maintenant à la fois de l’amplitude et du signe du courant appliqué. Il est important de noter que l’inductance sécante contient la contribution de l’aimant lui-même au flux concaténé, mais ce flux invariant dans le temps ne contribue pas à la tension rétro-induite. L’aimant n’agit que pour modifier la relation B-H des matériaux non linéaires présents. En d’autres termes, un aimant n’affectera pas la réponse d’un inducteur constitué uniquement de matériaux linéaires. Cependant, il est important de garder à l’esprit qu’un aimant introduira toujours un biais dans l’inductance sécante. Par conséquent, lorsqu’un aimant est présent dans votre modèle, il est toujours préférable de travailler avec l’inductance différentielle, même si tous les matériaux sont linéaires.

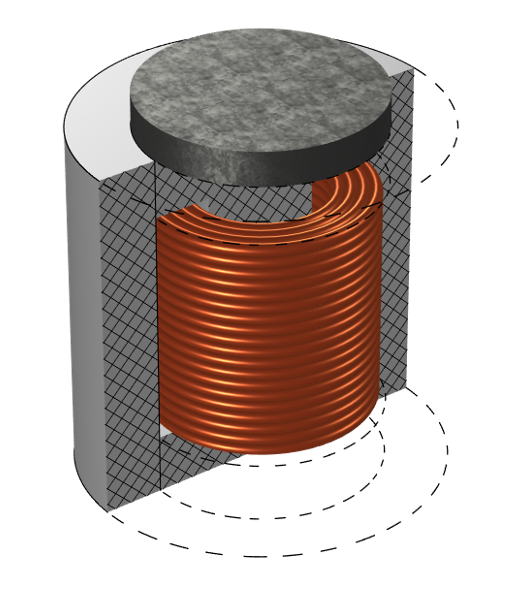
Un aimant placé au-dessus du noyau non linéaire B-H perturbera la réponse de ce dernier.

L’inductance différentielle n’est pas symétrique vis-à-vis du signe du courant DC dans le cas de l’inducteur polarisé.

Cette inductance différentielle peut à nouveau être utilisée pour construire un modèle de circuit électrique, et nous constatons à nouveau que les résultats concordent très bien, sauf pendant la période de démarrage. Ce désaccord durant le démarrage met en évidence l’écart entre le modèle résolvant les champs variant dans l’espace et l’évolution spatiale de la saturation du noyau d’une part, et le modèle réduit d’autre part.

Accord entre le modèle spatial à éléments finis et le modèle réduit de circuit comprenant l’inductance différentielle polarisée.

La réponse non linéaire d’un transformateur

Examinons ensuite un transformateur composé de deux bobines identiques enroulées autour d’un noyau en poudre d’alliage de ferrite. La symétrie peut être exploitée non seulement pour réduire la taille du modèle, mais aussi pour réduire la quantité de données à calculer, puisque L’_{11} = L’_{22} et L’_{12} = L’_{21}. Bien que, dans le cas général, les inductances différentielles puissent être fonction à la fois deI_1, le courant dans le primaire, et de I_2, le courant dans le secondaire, dans le cas de cette structure symétrique, on peut écrire que L'(I_1,I_2) = L'(|I_1+I_2|,0). En d’autres termes, il suffit de calculer les inductances différentielles L’_{11} et L’_{12} sur une plage de valeurs de I_1, tout en maintenant I_2=0, plutôt que de balayer les deux variables.

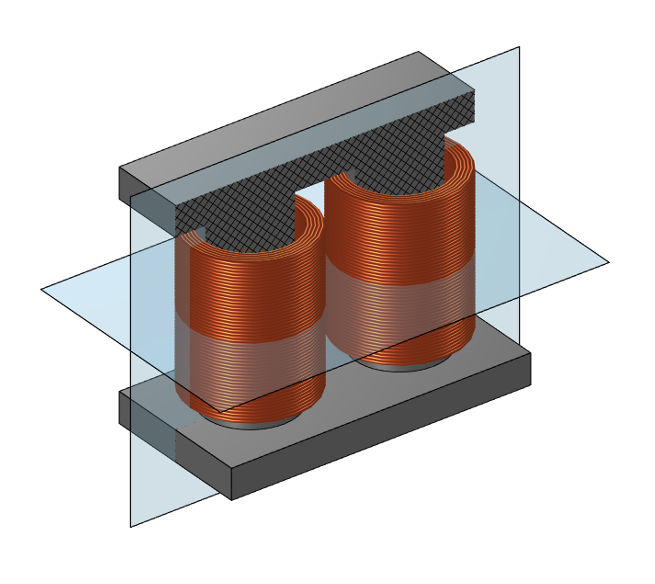
Un transformateur composé de deux bobines identiques enroulées autour d’un noyau symétrique. Les deux plans de symétrie sont représentés.

Une fois ces deux inductances différentielles calculées, un ensemble de fonctions est utilisé pour définir les quatre termes de la matrice d’inductance mutuelle. Ces termes peuvent être utilisés dans un modèle de circuit électrique représentant ce même transformateur. En raison de la non-linéarité, le couplage entre les deux bobines est modélisé à l’aide d’une fonctionnalité Source de tension, contrôle en courant, comme l’illustre la figure ci-dessous.

Le circuit équivalent d’un transformateur comportant un matériau de noyau non linéaire.

Résoudre la réponse de ce transformateur en utilisant le modèle tridimensionnel complet représente un coût de calcul important, tandis que la résolution du modèle de circuit électrique est très rapide. Les résultats concordent encore une fois très bien, même s’il est important que la matrice d’inductance différentielle soit calculée pour toutes les conditions de fonctionnement possibles. Ce coût initial de calcul de la matrice d’inductance différentielle peut être parallélisé via un batch paramétrique ou une analyse paramétrique sur cluster afin d’exploiter toutes les ressources informatiques disponibles.

Une tension sinusoïdale AC appliquée au primaire engendre un courant non linéaire traversant le primaire et le secondaire. On compare la tension sur le primaire et le courant sur le secondaire obtenus avec le modèle complet et le modèle de circuit électrique.

La réponse dynamique d’un solénoïde

Examinons maintenant un solénoïde composé d’une bobine placée à l’intérieur d’un boîtier en fer et traversée par un plongeur en fer. Le plongeur est monté de telle sorte qu’il ne peut se déplacer que le long de son axe. Nous supposerons que la perméabilité du fer est constante sur la plage des champs attendus et nous négligerons les non-linéarités des matériaux. Nous supposerons également que le boîtier et le plongeur sont composés de pièces collées ensemble par un matériau isolant, minimisant ainsi tout courant induit circulant autour de l’axe, et nous considérerons donc le fer comme étant sans perte.

Un solénoïde composé d’une bobine à l’intérieur d’un boîtier en fer avec un plongeur en fer maintenu en position par un ressort.

Un ressort maintient le plongeur dans sa position d’équilibre à l’extérieur du boîtier. Lorsqu’une tension est appliquée à la bobine, le courant commence à circuler et force le plongeur à se rapprocher du centre. Dans cette situation, il n’y a aucune non-linéarité de matériau, de sorte que le flux concaténé dépend linéairement du courant variable dans le temps, I, mais varie de manière non linéaire avec u, la position selon l’axe z du plongeur:

Ainsi, suivant théorème de dérivation des fonctions composées, la tension rétro-induite s’écrit:

Le premier terme tient compte du fait que l’inductance sécante varie lorsque le plongeur change de position. Le second terme introduit une tension rétro-induite supplémentaire lorsque le plongeur se déplace à la vitesse \dot{u} dans un champ magnétique non nul.

En gardant à l’esprit que le flux concaténé varie linéairement avec un courant DC imposé, I_{DC}, et en dérivant la première équation par rapport à la position lorsqu’un courant DC est appliqué, nous constatons que:

Pour calculer la dérivée par rapport à la position, nous utilisons l’interface Sensibilité et l’interface Maillage mobile pour calculer la dérivée partielle du flux concaténé par rapport à une variation infinitésimale, \delta, de la position selon z à un courant DC fixé:

Nous utilisons le Maillage mobile pour introduire un changement fini et infinitésimal, \delta, de la position selon z et considérons la dérivée partielle uniquement par rapport à ce déplacement infinitésimal, tout en balayant une plage de positions différentes, u, le long de la course du plongeur.

Cette dérivée partielle nous permet maintenant de construire un modèle réduit électromécanique simple couplant le modèle de circuit électrique à une équation décrivant le mouvement du plongeur.

Le modèle réduit électromécanique se compose d’un modèle de circuit électrique et d’un modèle réduit mécanique couplés par le terme de force, par l’inductance sécante dépendant de la position et par la tension lors du déplacement du plongeur.

Comme le montre le schéma du système réduit, le système électrique est couplé au système mécanique par l’intermédiaire de la force. Pour comprendre comment nous arrivons à l’expression de cette force, examinons l’expression de l’énergie magnétique totale dans le système, qui varie en fonction du courant et de la position du plongeur:

La force totale sur le plongeur peut être déterminée par la méthode du travail virtuel. Dans le cas de matériaux magnétiques linéaires, la force dans la direction axiale s’obtient en prenant la dérivée partielle de l’énergie magnétique totale par rapport à un déplacement infinitésimal. On peut donc écrire:

En d’autres termes, la force est une fonction du courant traversant la bobine et de la dérivée partielle de l’inductance par rapport à la position, que nous avons déjà calculée. Ainsi, en plus de notre modèle du solénoïde, nous résolvons simultanément l’équation différentielle ordinaire pour la position du plongeur:

où u_0 est la position d’équilibre du plongeur. Cette équation peut être résolue via une interface EDO et EAD globales distincte ou via une fonctionnalité Equations globales qui peut être ajoutée à n’importe quelle interface physique. On peut donc utiliser cette équation pour résoudre le mouvement en même temps que l’interface Champs magnétiques, ou même l’associer à l’interface Circuit électrique.

Nous laissons le plongeur osciller librement le long de l’axe et examinons les résultats obtenus pour un jeu de paramètres d’entrées produisant une dynamique intéressante afin d’illustrer le fait que le modèle réduit concorde très bien avec le modèle spatial utilisé pour calculer les paramètres réduits.

Comparaison entre le modèle détaillé de champs magnétiques du solénoïde et le modèle réduit.

Construire ses propres modèles réduits

Nous avons examiné ici une série de quatre exemples mettant en évidence les capacités du logiciel COMSOL Multiphysics^® à extraire non seulement l’inductance différentielle, mais aussi la dérivée du flux concaténé de la bobine par rapport à d’autres variables d’entrée. Les quantités résultantes peuvent être utilisées pour construire des modèles réduits légers susceptibles de prédire correctement les performances du système.

Vous souhaitez extraire des inductances différentielles et construire ce type de modèles réduits ? Téléchargez les exemples suivants dans la Bibliothèque d’applications:

Référence

1. 1. D. Cheng, “Field and Wave Electromagnetics”, 2nd ed., Addison-Wesley, 1991