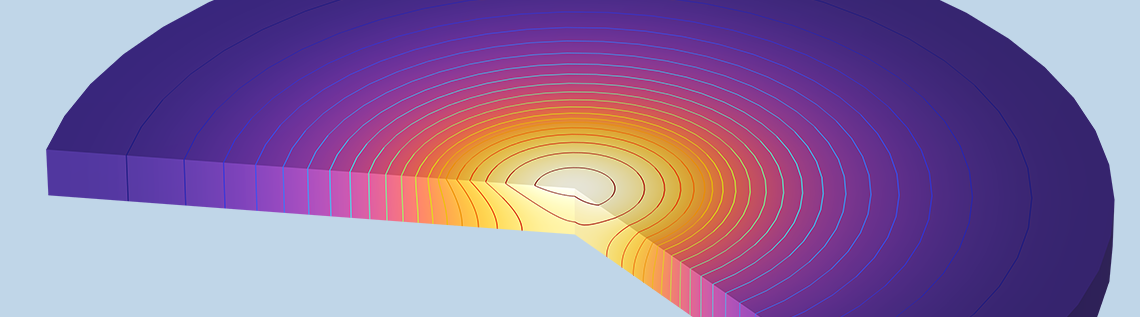
Introduction à la modélisation du transfert de chaleur transitoire des solides dans COMSOL Multiphysics®
Le logiciel COMSOL Multiphysics® est souvent utilisé pour modéliser le transfert thermique transitoire de solides. Les modèles de transfert de chaleur transitoire sont faciles à mettre en place et à résoudre, mais ils ne sont pas exempts de difficultés. Par exemple, l’interprétation de leurs résultats peut dérouter même un utilisateur avancé de COMSOL®. Dans cet article de blog, nous explorerons un modèle simple de transfert thermique transitoire et l’utiliserons pour acquérir une compréhension approfondie de ces nuances.
Un problème simple de transfert de chaleur transitoire
La Figure 1 illustre le scénario de modélisation qui fait l’objet de cet article de blog. Dans ce scénario, un chargement thermique uniforme spatialement est appliqué à une région circulaire sur la surface supérieure d’un cylindre d’un matériau qui a une température initiale uniforme. La valeur du chargement est initialement élevée, mais diminue au bout d’un certain temps. En complément de l’application de ce chargement thermique, une condition aux limites est incluse pour modéliser le rayonnement thermique de l’ensemble de la surface supérieure, ce qui refroidit la pièce. Il est supposé que les propriétés matériaux (conductivité thermique, densité et chaleur spécifique) et l’émissivité de surface restent constantes dans la plage de température envisagée. Il est également supposé qu’aucune autre physique n’entre en jeu. L’objectif de ce modèle est de pouvoir l’utiliser pour calculer la distribution de la température dans le matériau au cours du temps.
Un scénario de modélisation similaire est présenté dans notre modèle tutoriel Chauffage par laser d’une plaque de silicium, mais gardons à l’esprit que les enseignements discutés ici sont applicables à tout cas impliquant du transfert de chaleur transitoire.
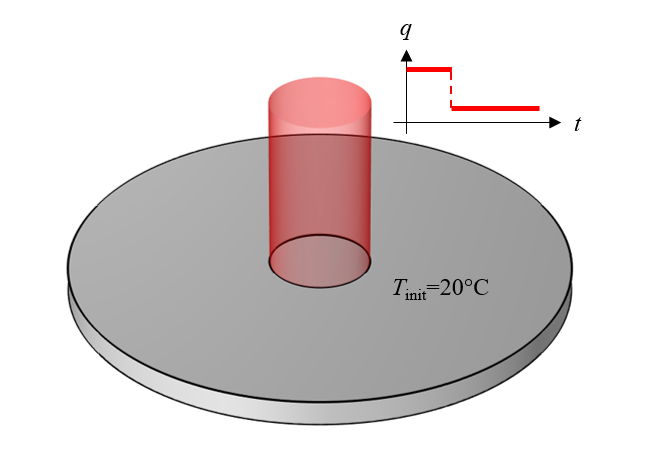
Figure 1. Un cylindre de matière dont la surface supérieure est soumise à une source de chaleur.
Bien qu’il soit tentant de commencer à mettre en place notre modèle en dessinant la géométrie exacte illustrée sur la Figure 1, nous commencerons par un modèle plus simple. Sur la Figure 1, nous pouvons voir que la géométrie et le chargement sont axialement symétriques vis-à-vis de l’axe central, nous pouvons donc raisonnablement en déduire que la solution sera également axialement symétrique. Par conséquent, nous pouvons simplifier notre modèle en le ramenant au plan de modélisation 2D axisymétrique. (Découvrez comment exploiter la symétrie pour réduire la taille des modèles ici.)
Le flux de chaleur est uniforme sur une zone circulaire au centre. La manière la plus simple de modéliser cela est de modifier la géométrie en introduisant un point sur la frontière de notre domaine 2D. Ce point divise la frontière en deux parties, l’une chauffée et l’autre non chauffée. L’ajout de ce point à la géométrie garantit que le maillage résultant est exactement aligné sur cette variation du flux de chaleur. En gardant tout cela à l’esprit, nous pouvons créer un modèle de simulation (Figure 2) qui est à la fois 2D axisymétrique et équivalent au modèle 3D.
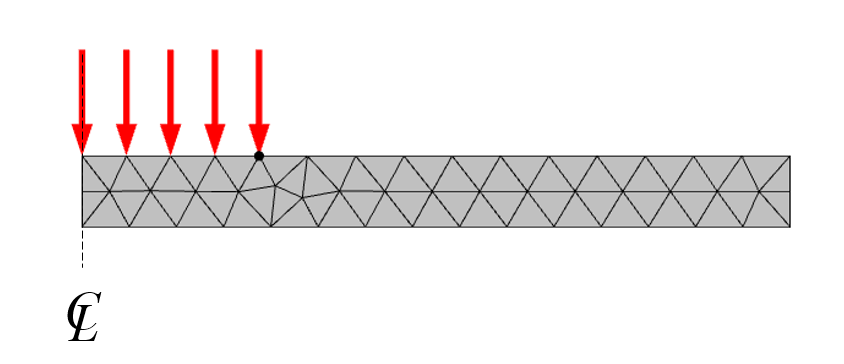
Figure 2. Le modèle 2D axisymétrique équivalent au modèle 3D, représenté avec le maillage par défaut.
Le cas que nous étudions comprend également un changement instantané de la valeur du flux de chaleur appliqué; à t = 0.25 s, il diminue de valeur. De tels changements de chargements doivent être traités en utilisant l’interface Evènements, comme décrit dans cet article de la Base de Connaissances sur la résolution de modèles avec des variations en échelon pour les chargements temporels. En bref, l’interface Evènements indique au solveur le moment exact où le changement de chargement se produit et le solveur ajuste le pas de temps en conséquence. Nous pourrions également souhaiter connaître les pas de temps pris par le solveur afin de modifier les paramètres du solveur pour obtenir les résultats aux pas de temps pris par le solveur, et nous pouvons alors représenter la température du point situé au centre supérieur de la pièce, comme illustré par la Figure 3.
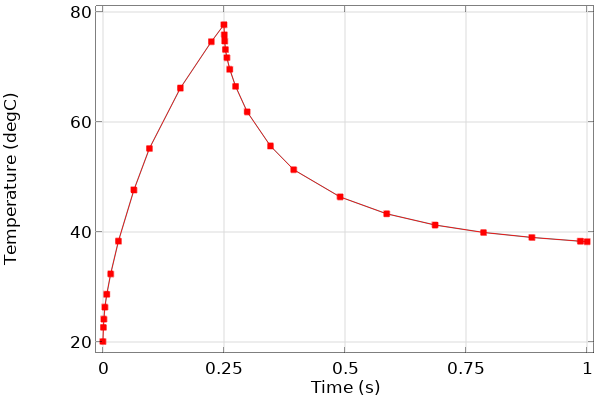
Figure 3. Graphique de la température en fonction du temps en un même endroit, avec des points montrant que les pas pris par le solveur sont plus courts à proximité des changements abrupts des chargements.
Ensuite, nous réexécutons le calcul du modèle pour différentes valeurs de la tolérance relative du solveur et nous comparons les résultats dans un graphique (Figure 4). Ce type de graphique nous montre que les solutions convergent rapidement vers les mêmes valeurs quand la tolérance est réduite, comme attendu.
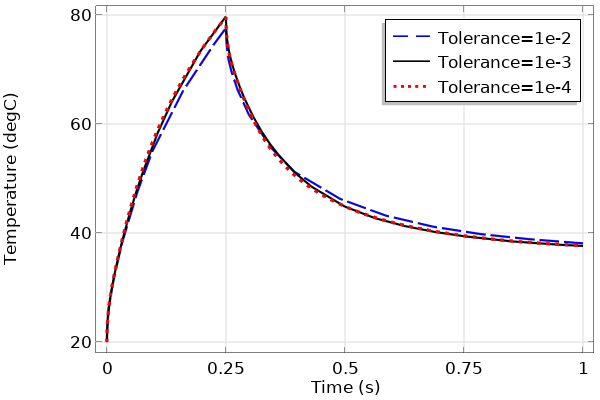
Figure 4. Graphique de la température en un même point en fonction du temps, calculé pour différentes valeurs de tolérance relative.
Une autre quantité qui peut être évaluée ici est la quantité totale d’énergie entrant dans le domaine. Nous pouvons intégrer l’expression du flux de chaleur total, ht.nteflux, sur les frontières, et nous pouvons utiliser l’opérateur timeint() pour l’intégrer dans le temps afin d’obtenir l’énergie totale. Les résultats de cette intégrale sont présentés dans le tableau ci-dessous pour une valeur croissante de tolérance relative du solveur temporel. (Suggestion: pour en savoir davantage sur le calcul des intégrales spatiales et temporelles, consultez cet article de la Base de Connaissances, et apprenez-en davantage sur le calcul des bilans d’énergie dans cet article de blog sur comment calculer la conservation de la masse et le bilan d’énergie.)
| Tolérance relative du solveur | Intégrale temporelle du flux entrant dans le domaine de modélisation (J) |
|---|---|
| 1e-2 | 32.495 |
| 1e-3 | 32.469 |
| 1e-4 | 32.463 |
Ce que nous observons à partir des résultats, c’est que l’énergie totale dans le système est en fait presque indépendante de la tolérance du solveur temporel. À première vue, cela semble être une validation fantastique de notre modèle. Cependant, il est important de souligner que ce que nous observons ici est la propriété mathématique fondamentale de la méthode des éléments finis (MEF). En bref, l’énergie totale s’équilibre toujours très bien. Cela ne signifie pas qu’il n’y a pas d’erreurs dans le modèle, les erreurs apparaissent simplement à des endroits différents… alors allons les chercher maintenant.
Les erreurs: elles sont faciles à commettre, mais difficiles à déterminer
Il convient de marquer une pause et d’aborder avec beaucoup de prudence un mot du paragraphe ci-dessus, le mot erreur, qui est souvent utilisé dans le monde de la modélisation et de la simulation sans contexte ou avec une précision insuffisante. Dans la suite de ce paragraphe, nous présenterons quelques descriptions détaillées de différentes erreurs qui peuvent apparaître dans une multitude de scénarios de modélisation. (Si vous souhaitez passer directement à la partie relative aux erreurs dans notre modèle, cliquez ici.)
Erreurs d’entrées
Une erreur dans les données d’entrée, comme son nom l’indique, est une erreur dans la définition d’un modèle, par exemple lorsque les propriétés des matériaux ne sont pas saisies correctement ou lorsque la géométrie est dessinée de manière erronée. L’une des erreurs de données d’entrée les plus néfastes est l’erreur d’omission, par exemple lorsqu’une condition aux limites est oubliée. Les erreurs d’entrée se distinguent des incertitudes dans les données d’entrée, qui peuvent par exemple survenir lorsque les propriétés exactes des matériaux ne sont pas connues. Le premier problème ne peut être résolu que par une gestion rigoureuse des données, tandis que le second peut l’être par l’intermédiaire du Module Uncertainty Quantification. Pour notre exemple, nous considérerons qu’il n’y a pas d’erreurs ou d’incertitudes dans les données d’entrée.
Erreurs de discrétisation de la géométrie
Une erreur de discrétisation de la géométrie survient lors de la discrétisation de la géométrie via le maillage éléments finis, en particulier lors du maillage de frontières non planes. Ces erreurs diminuent avec le raffinement du maillage et peuvent être évaluées sans avoir à résoudre un modèle par éléments finis. Étant donné que notre domaine de modélisation 2D axisymétrique n’a pas de frontières courbes, nous n’aurons pas non plus à nous préoccuper de ce type d’erreur.
Erreurs de discrétisation de la solution
Une erreur de discrétisation de la solution résulte du fait que les fonctions de base des éléments finis ne peuvent pas représenter parfaitement le véritable champ de la solution et ses dérivées dans ce domaine. Elle est fondamentalement présente dans la méthode des éléments finis. Cette erreur, qui est intrinsèquement liée à l’erreur de discrétisation géométrique, est toujours présente et est toujours réduite par le raffinement du maillage pour tout problème d’éléments finis bien posé.
Erreurs de discrétisation temporelle
Comprendre la propagation des erreurs dans un modèle temporel est assez complexe. Pour les besoins de cet article de blog, il est suffisant de souligner que toute erreur introduite ou déjà présente à un pas de temps donné se propagera vers les pas suivants, mais que pour le type de problème diffusif que nous traitons ici, elle se dissipera. Ce type d’erreur est systématiquement présent, et sa taille est contrôlée à la fois par la tolérance du solveur temporel et par le maillage.
Erreurs d’interprétation
Il existe un autre type d’erreur qui est un peu plus qualitatif : l’erreur d’interprétation. Ces erreurs se produisent lorsque la signification des résultats et la manière dont ils ont été obtenus ne sont pas comprises avec précision. L’une des plus connues concerne la singularité dans les angles vifs, une situation qui survient souvent en mécanique des structures ainsi que dans le cadre de la modélisation des champs électromagnétiques. Les erreurs d’interprétation sont particulièrement fréquentes lorsque des erreurs d’entrée sont présentes. Par conséquent, si vous n’êtes pas sûr de vos résultats, il est important de revenir en arrière et de revérifier (ou même de revérifier une troisième fois!) toutes les données d’entrée de votre modèle.
Cette liste n’est pas exhaustive. Par exemple, nous pourrions également parler des erreurs numériques dues à la précision finie du solveur du système linéaire, du solveur du système non linéaire et de l’erreur d’intégration numérique. Toutefois, ces erreurs, ainsi que d’autres types d’erreurs, sont toujours beaucoup moins significatives.
Cette liste de définitions étant établie, nous sommes maintenant prêts à revenir à notre modèle.
Repérer les erreurs spatiales et temporelles
Jusqu’à présent, nous avons examiné la solution en un point du modèle et observé que la solution semble très bien converger à mesure que nous affinons la tolérance relative du solveur temporel, de sorte que nous devrions déjà avoir compris l’idée que la diminution de la tolérance relative du solveur temporel diminuera l’erreur temporelle. Examinons maintenant la distribution spatiale de la température. Nous commencerons par la température le long de l’axe central et, pour la tolérance la plus élevée de 1e-2, nous examinerons la solution au temps initial ainsi qu’au premier pas de temps pris par le solveur, sur le graphique ci-dessous.
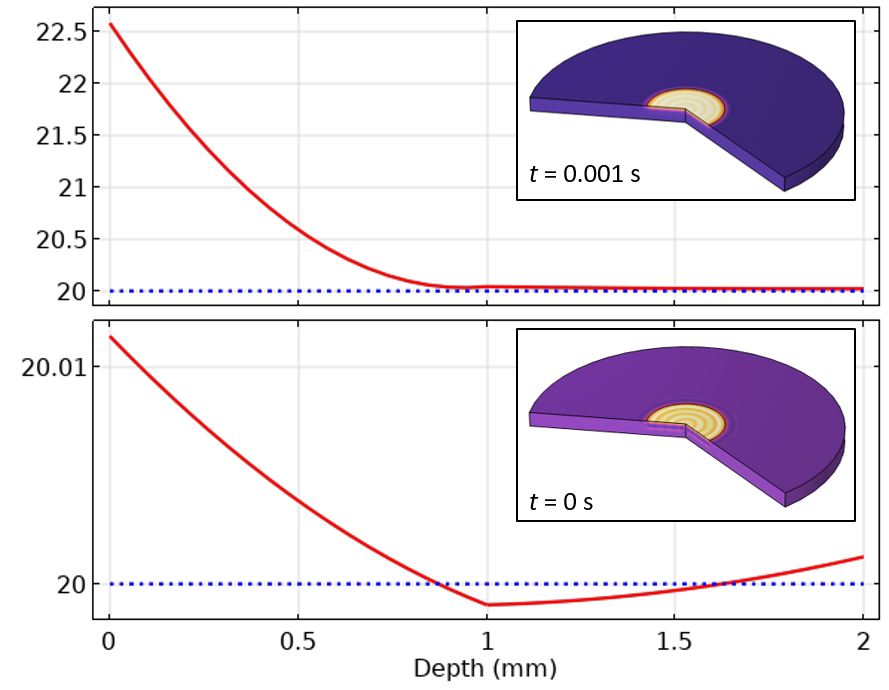
Figure 5. Graphique de la température de l’axe central au temps initial et au premier pas de temps.
Le graphique de la valeur initiale montre que la température le long de l’axe central ne correspond pas à la température initiale spécifiée — à certains endroits, elle est même inférieure à la valeur initiale. Cela est dû au fait que COMSOL Multiphysics® utilise une initialisation dite consistante, qui ajuste le champ solution au temps initial pour qu’il soit cohérent avec les conditions aux limites et les valeurs initiales spécifiées. L’initialisation consistante consiste à prendre un très petit pas de temps artificiel supplémentaire, que l’on peut considérer comme se déroulant sur un intervalle de temps nul. L’initialisation consistante peut être désactivée dans les paramètres du solveur pour le pas de temps initial, ainsi que dans les fonctionnalités Evènements explicites et Evènements implicites, mais cela doit être fait avec prudence. Dans un modèle multiphysique plus général, en particulier ceux qui impliquent l’écoulement de fluides, il peut être plus robuste de la laisser activée par défaut, c’est pourquoi nous traiterons cette situation ici.
Dans ce contexte, l’initialisation consistante permet d’ajuster le champ de température en fonction des chargements appliqués et des conditions aux limites. Comme le chargement thermique appliqué est initialement non nul, le gradient du champ de température, qui est proportionnel au flux de chaleur, doit également être initialement non nul. Nous devons également tenir compte du fait que ce champ est discrétisé à l’aide des fonctions de base des éléments finis. Le long de l’axe central, ces fonctions de base sont des polynômes, mais un polynôme ne peut pas correspondre exactement à la vraie solution; par conséquent, ce que nous obtenons après l’étape d’initialisation consistante est une solution qui sera légèrement supérieure ou inférieure au résultat attendu. À partir de la solution du premier pas de temps, nous pouvons également constater que la température du côté le plus éloigné de la pièce augmente déjà, ce qui est inattendu. Bien que ces variations par rapport à nos attentes soient très faibles, nous aimerions les minimiser.
Avant de modifier notre modèle pour réduire ces erreurs de discrétisation de la solution, appliquons un peu d’intuition physique au problème. Au début de la simulation, la distribution de la température le long de I’axe central sera assez similaire à la solution d’un scénario de modélisation qui implique la simulation du transfert de chaleur à travers une plaque unidimensionnelle. Une solution analytique existe déjà pour ce type de scénario de modélisation, qui est souvent abordé dans de nombreux ouvrages sur l’analyse du transfert de chaleur. (Cet exemple est d’ailleurs utilisé pour illustrer la couverture de l’un des manuels que j’ai sur mon bureau, intitulé Fundamentals of Heat and Mass Transfer.)
Par souci de concision, nous ne présenterons pas la solution analytique et nous nous contenterons de donner le résultat: lorsque vous appliquez une source de chaleur à une partie de la surface, la température à la surface commence à augmenter et, par la suite, la partie interne se réchauffe elle aussi. Notez qu’il faut plus de temps pour que les points plus éloignés de la limite se réchauffent. La température à l’intérieur de la plaque ne variera pas de manière homogène: les points situés à l’intérieur de la plaque mettront plus de temps à changer de température que les points situés à proximité de la surface. Il est important de noter que les variations spatiales de température s’atténuent avec le temps en raison de la nature diffusive de l’équation de transfert de chaleur. Maintenant que nous avons compris, revenons à notre modèle et voyons comment l’améliorer.
En bref, pour minimiser l’erreur de discrétisation de la solution, nous devons mailler plus finement les zones où les champs varient de manière significative. D’après notre intuition (ou la solution analytique, si nous voulons la consulter), nous savons que les champs varient de manière significative très près de la surface et dans la direction normale à la frontière, mais que ces variations sont plus lissées à l’intérieur. C’est exactement le genre de situation qui nécessite le maillage de type couche limite, qui crée des éléments fins dans la direction normale aux frontières, comme le montre la Figure 6.
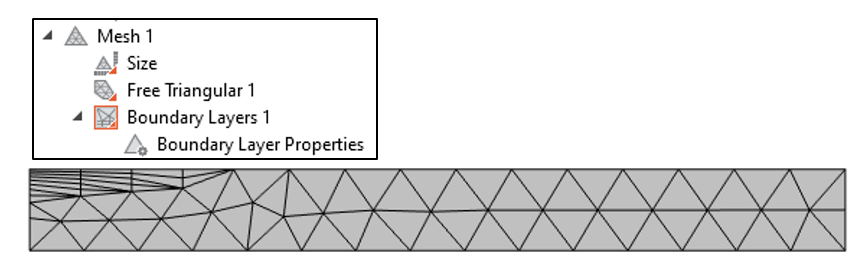
Figure 6. La séquence de maillage est modifiée par l’ajout d’une fonctionnalité Couches limites le long d’une frontière sur la partie supérieure de la plaque.
Nous pouvons maintenant relancer la simulation et afficher la solution au temps initial et au pas de temps suivant.
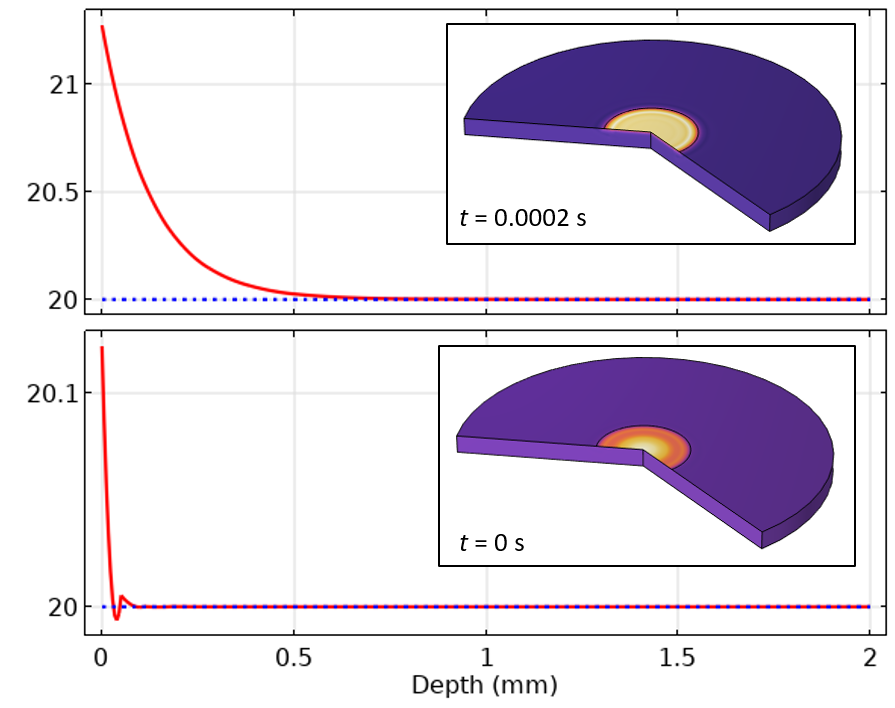
Figure 7. Graphique de la température de l’axe central au pas de temps initial et au premier pas de temps lorsqu’on utilise le maillage de type couche limite.
Sur la Figure 7, nous pouvons observer que la sous-estimation de la valeur initiale de la température est beaucoup plus localisée dans l’espace. Il s’avère que l’utilisation d’un maillage plus fin permet également au solveur temporel d’effectuer des pas de temps plus petits. Ainsi, en affinant le maillage, nous avons réduit les erreurs de discrétisation spatiale et temporelle.
Nous pouvons également examiner les résultats le long de la frontière supérieure du domaine de modélisation, représentant la distribution de la température sur la surface exposée. Sur la Figure 8, cette distribution est représentée au temps initial et au premier pas de temps, avec une tolérance de 1e-2. Sur ces graphiques, nous pouvons observer un champ oscillant de façon assez spectaculaire spatialement. Il s’agit d’un symptôme de la discrétisation spatiale. Gardez à l’esprit que notre chargement thermique subit un changement de valeur par palier le long de l’axe radial, et que ce que nous observons ici s’apparente quelque peu au phénomène de Gibbs.
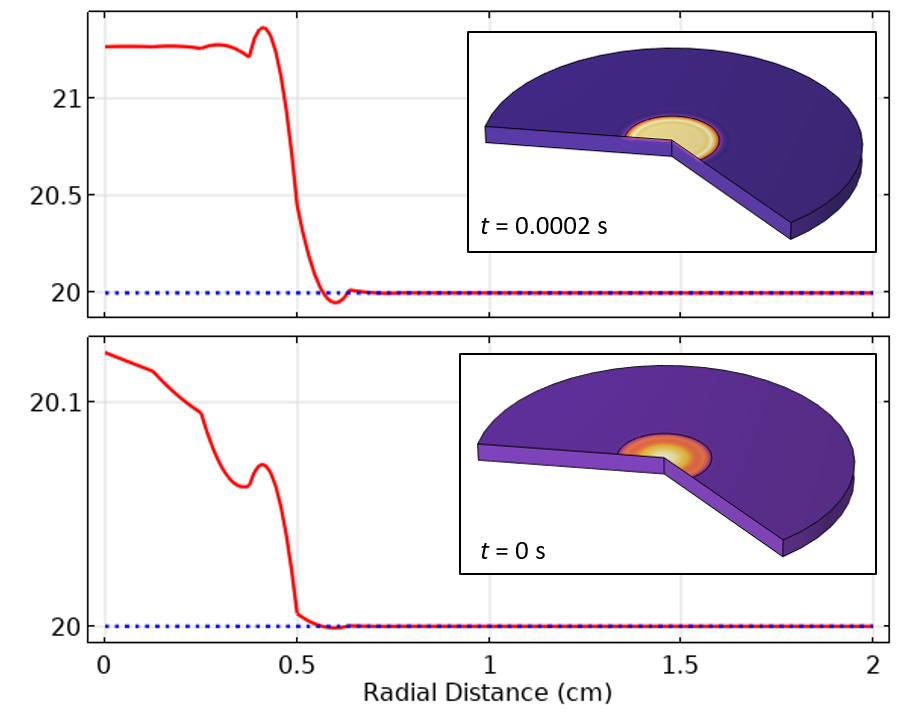
Figure 8. Graphique de la température le long de la surface supérieure à la valeur initiale et au premier pas de temps, en utilisant le maillage de type couche limite.
La solution est similaire à la précédente, mais nous devons maintenant raffiner le maillage dans la zone de transition. Pour ce problème, il est possible d’appliquer un réglage plus fin de Taille au point de délimitation, ce qui donne le maillage représenté ci-dessous.
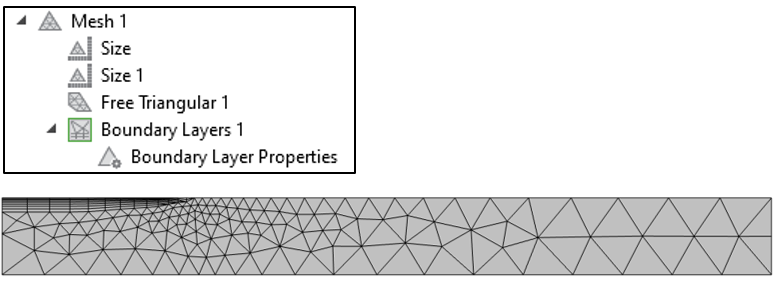
Figure 9. Graphique des paramètres de Maillage et du maillage, avec une taille de maille plus petite appliquée au point délimitant la distribution du chargement thermique.
Les résultats de température de la Figure 10 montrent que les oscillations de la solution sont maintenant réduites et ne se propagent pas autant dans l’espace ou dans le temps. Même avec une tolérance relative du solveur de 1e-2, la solution est déjà nettement améliorée.
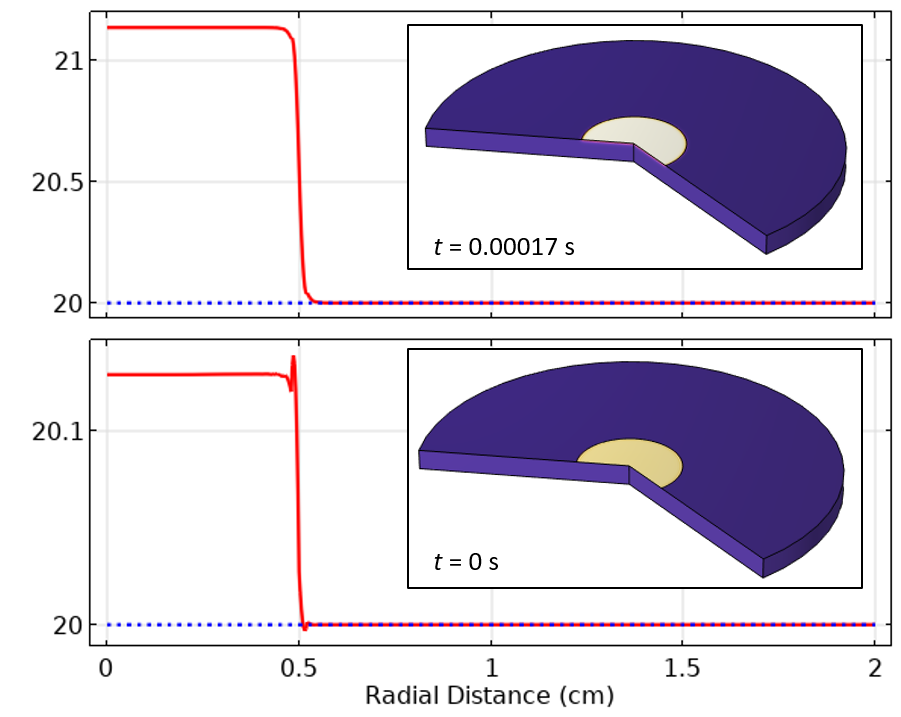
Figure 10. Après avoir raffiné le maillage, et en utilisant une tolérance relative de 0.01, la température le long de la surface supérieure au temps initial et au premier pas de temps est beaucoup plus précise.
Il est possible de poursuivre cet exercice en raffinant encore davantage le maillage et la tolérance du solveur. Mais grâce aux raffinements que nous avons effectués jusqu’à présent, nous pouvons déjà commencer à voir que les erreurs diminuent rapidement — et même les erreurs qui sont encore présentes sont lissées à la fois dans l’espace et dans le temps en raison de la nature diffusive de l’équation de transfert de chaleur en régime transitoire. En fait, nous devrions probablement consacrer autant d’efforts à l’étude des conséquences des incertitudes dans les données d’entrée de nos modèles.
Quels sont les autres éléments susceptibles d’entrer en jeu ?
Dans cet exemple, le chargement thermique appliqué sur la frontière ne se déplace pas dans le temps, de sorte que l’approche consistant à partitionner les frontières est raisonnable. Si la distribution du chargement thermique devait se déplacer, l’ensemble du maillage de la surface chauffée devrait être plus raffiné. (Découvrez ici trois approches pour modéliser les chargements et les contraintes en mouvement dans COMSOL®.)
Plus haut dans cet article de blog, il a été mentionné que les propriétés des matériaux sont supposées constantes en fonction de la température et ne dépendent d’aucun autre facteur physique. Il s’agit d’une simplification importante, car toutes les propriétés des matériaux changent avec la température. Les matériaux peuvent même subir un changement de phase, comme la fusion. Le changement de phase peut être modélisé de différentes manières, notamment par la méthode de la capacité thermique apparente, qui utilise une chaleur spécifique hautement non linéaire pour tenir compte de la chaleur latente du changement de phase. Nous pourrions également facilement envisager qu’il soit question d’un problème multiphysique, tel qu’une équation de réticulation thermique, ou même d’un problème de chauffage électromagnétique non linéaire d’un matériau. Dans ce cas, nous devrions surveiller la convergence non seulement du champ de température, mais aussi de toutes les autres variables de champ en cours de résolution, et peut-être même de leurs dérivées temporelles et spatiales. Ces cas peuvent tous nécessiter un maillage très fin partout dans le domaine de modélisation, si bien que les leçons tirées de cette situation simple ne sont pas valables. Cependant, même lors du maillage et de la résolution de modèles beaucoup plus complexes, il est toujours bon de garder à l’esprit le cas le plus simple possible (même s’il ne sert que de point de départ conceptuel).
De plus, nous devons insister sur le fait que cet article ne concerne que le chauffage d’un matériau solide en fonction du temps. En présence d’un fluide en mouvement, les équations de base changent considérablement; le maillage des modèles d’écoulement de fluides est un sujet distinct et relativement plus complexe. Pour les problèmes de type ondulatoire, la sélection des réglages du maillage et du solveur devient un peu plus simple.
Conclusion
Dans cet article de blog, nous avons examiné un problème typique de modélisation du transfert de chaleur. Nous avons observé que certaines erreurs apparaissent dans la solution à proximité de changements brusques des chargements, à la fois dans l’espace et dans le temps. Les lecteurs devraient maintenant comprendre de quels types d’erreurs il s’agit et savoir qu’elles sont une conséquence inhérente à la méthode des éléments finis qui, comme toutes les méthodes numériques, n’est qu’une approximation de la réalité. Bien que ces erreurs puissent sembler importantes, leur ampleur diminue dans l’espace et le temps en raison de la nature diffusive de l’équation de transfert de chaleur transitoire. Nous avons montré que le raffinement du maillage permet de réduire les erreurs de discrétisation spatiale, ce qui a pour effet implicite de réduire les erreurs de pas de temps. Enfin, nous avons discuté de la manière dont les erreurs de pas de temps peuvent être encore réduites avec le raffinement de la tolérance relative du solveur.
Il convient également de faire un résumé encore plus bref: si vous êtes principalement intéressé par la solution après un temps relativement long, il est tout à fait acceptable d’utiliser un maillage assez grossier et une tolérance relative du solveur par défaut. En revanche, si vous vous intéressez aux variations de température à courte durée et à petite échelle, vous devez vous pencher à la fois sur la tolérance relative du solveur et sur le raffinement du maillage.
Grâce à cette compréhension, nous pouvons éviter de commettre des erreurs d’interprétation. Cela nous permettra de construire des modèles plus complexes à partir de modèles simples avec confiance et facilité.
Prochaine étape
Essayez vous-même le modèle présenté dans cet article de blog en cliquant sur le bouton ci-dessous, qui vous conduira à la Bibliothèque d’Applications :



Commentaires (0)