Comment modéliser différents types d’amortissement dans COMSOL Multiphysics^®

Dans un précédent article de blog, nous avons présenté divers phénomènes physiques responsables de l’amortissement dans les structures et montré comment cela peut être représenté mathématiquement. Aujourd’hui, nous poursuivons en examinant comment inclure concrètement l’amortissement dans les modèles d’éléments finis.

Comment prendre en compte l’amortissement dans l’analyse par éléments finis

Lors d’une analyse de dynamique des structures, la modélisation de l’amortissement peut être une étape importante et difficile du processus.

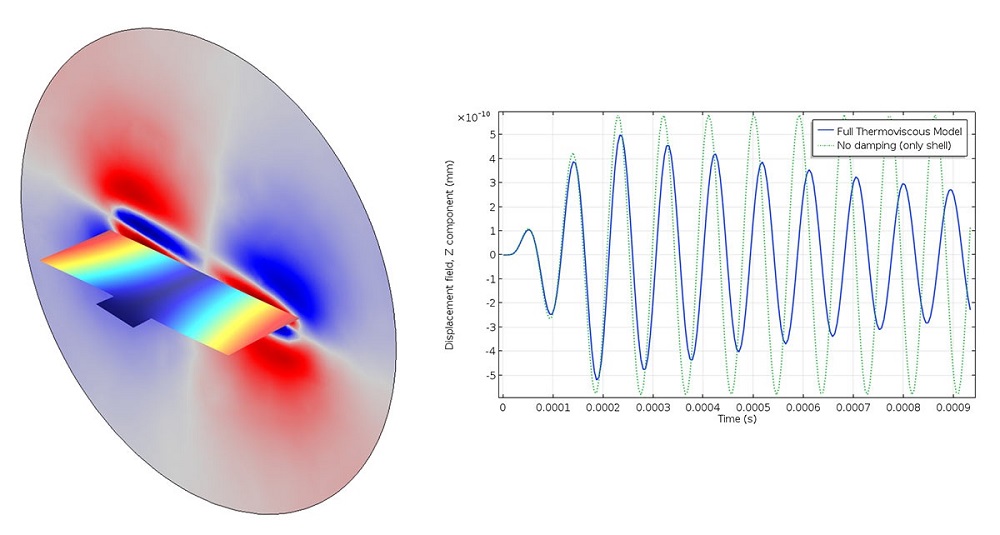
Analyse transitoire d’un micromiroir vibroacoustique, avec prise en compte de l’amortissement visqueux et thermique.

Découvrez un aperçu des éléments à prendre en compte lors de la modélisation des effets d’amortissement dans vos analyses par éléments finis avec le logiciel COMSOL Multiphysics®.

Analyse des fréquences propres

Un problème de fréquences propres peut être résolu avec ou sans amortissement dans COMSOL Multiphysics. Tout effet dissipatif présent dans votre modèle sera pris en compte, et les fréquences propres calculées seront à valeurs complexes. Ceci est automatique, vous n’avez donc pas besoin d’ajouter des réglages spécifiques dans le solveur.

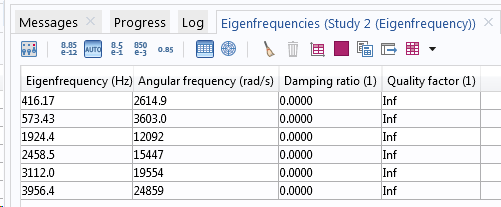
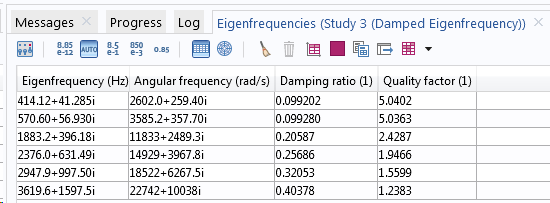
Fréquences propres d’un modèle avec (tableau du haut) et sans (tableau du bas) amortissement.

Dans la plupart des cas avec amortissement, non seulement les fréquences propres sont à valeurs complexes mais les modes propres le sont également. L’interprétation d’une déformée modale à valeurs complexes est que l’angle de phase fournit des informations sur le déphasage entre différents points de la structure en vibrations libres. En d’autres termes, si les déplacements en deux points ont différents angles de phases, ils n’atteindront pas leurs valeurs maximales simultanément.

Dans la plupart des cas, les effets de l’amortissement sur les déformées modales et les fréquences propres sont marginaux. La raison principale d’inclure l’amortissement dans une analyse de fréquences propres est d’estimer dans quelle mesure les différentes résonances seront amorties.

Analyse de réponse en fréquence

Si la fréquence d’excitation est proche d’une fréquence propre (disons à ±50%), le modèle d’amortissement est d’une importance primordiale, comme le montrent les courbes de réponse dans le blog précédent. C’est un cas où il est vraiment primordial d’obtenir des valeurs adéquates de l’amortissement. Proche de la résonance, les résultats sont complètement dépendant de l’amortissement, de sorte que le choix entre un facteur de perte de 0,01 ou 0,02 peut, en fin de compte, signifier un facteur de 2 dans la prédiction des contraintes.

Analyses temporelles

Dans une analyse temporelle, l’amortissement aura, dans la plupart des cas, un impact limité sur les résultats. Les exceptions sont les simulations de propagation d’onde ou si l’historique des chargements est tel que certaines résonances soient fortement excitées.

Il existe, cependant, un autre aspect important de l’amortissement dans l’analyse temporelle: il peut stabiliser les pas de temps. Il est fréquent que des ondes parasites, moins intéressantes, soient générées dans la structure. A moins d’être correctement supprimées, les pas de temps peuvent devenir inutilement petits. Pour supprimer ces ondes, il est avantageux d’introduire un modèle d’amortissement qui fournit principalement un amortissement significatif aux hautes fréquences.

Analyse de spectre de réponse

Dans une analyse de spectre de réponse, l’amortissement fait partie de la modélisation du spectre de réponse, et ne doit donc pas être modélisé explicitement. Une seule valeur d’amortissement est utilisée pour représenter l’ensemble de la structure.

Modèles numériques pour l’amortissement

La formulation des éléments finis

Sous forme matricielle, les équations du mouvement discrétisées par éléments finis peuvent être écrites comme suit

Où M est la matrice de masse, C est la matrice d’amortissement visqueux, K est la matrice de rigidité, u est le vecteur déplacements, et le membre de droite est constitué du vecteur forces f.

Les matrices de masse et de rigidité sont calculées à partir de la géométrie et des propriétés matériaux de base, tels que la masse volumique et le module d’Young. La matrice d’amortissement peut, cependant, être formées de nombreuses façons différentes. Il est souvent possible de combiner différents types de contributions à l’amortissement.

Dans le domaine fréquentiel, où l’excitation et la réponse sont supposées harmoniques, l’équation correspondante est

Ici, les vecteurs déplacements et forces sont à valeurs complexes.

Facteur de perte

Le facteur de perte est la principale méthode pour décrire les pertes du matériau dans une analyse en domaine fréquentiel. La description mathématique se fait, comme vu dans le blog précédent, par un multiplicateur de la rigidité à valeur complexe.

Dans COMSOL Multiphysics, vous pouvez inclure un facteur de perte grâce au sous-noeud Amortissement d’une loi de comportement. Pour la loi de comportement Matériau élastique linéaire, vous pouvez même spécifier des facteurs de perte individuels pour les différents éléments de la matrice constitutive.

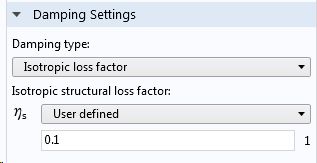
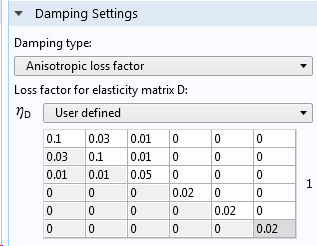
Saisie des valeurs de facteur de perte.

En réalité, il est courant que le facteur de perte dépende de la fréquence. Dans une analyse de réponse en fréquence, il est aisé d’incorporer cette dépendance en définissant le facteur de perte en tant que fonction de la variable prédéfinie freq. Vous pouvez utiliser une expression, comme indiqué ci-dessous, ou faire référence à tout autre type de fonction dépendant de la fréquence.

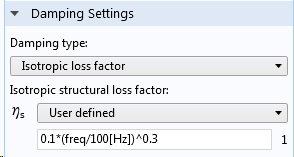
Facteur de perte dépendant de la fréquence.

Pour voir comment le facteur de perte intervient dans le système d’équations, supposons que le même facteur de perte soit utilisé partout. La matrice d’amortissement est alors définie comme suit

L’équation du mouvement devient donc

Amortissement visqueux

Dans un modèle d’amortissement visqueux, des contraintes proportionnelles à la vitesse de déformation apparaissent dans le solide.
Dans le cas le plus général, le tenseur reliant les contraintes à la vitesse de déformation peut contenir 21 constantes indépendantes. L’amortissement étant difficile à mesurer et à quantifier, ces valeurs sont rarement connues, il est plus courant de travailler avec des modèles d’amortissement visqueux isotropes.

L’amortissement visqueux dans l’interface Mécanique du solide de COMSOL Multiphysics utilise deux constantes:

• Viscosité de volume, \eta_b
• Viscosité de cisaillement, \eta_v

La première fournit un amortissement proportionnel à la variation de volume, et la seconde à la variation de forme.

Le tenseur des contraintes visqueuses peut s’écrire

Où \epsilon_v est la déformation volumétrique et {\boldsymbol \epsilon}_d est la partie déviatorique du tenseur des déformations.

Etant donné que la contrainte d’amortissement est proportionnelle à la vitesse de déformation, elle sera plus importante aux fréquences élevées.

L’amortissement visqueux est une autre option du noeud Amortissement.

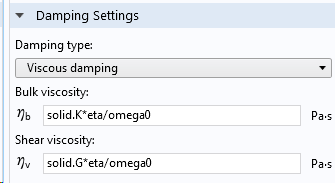
Saisie des paramètres de l’amortissement visqueux.

L’amortissement visqueux peut être utilisé dans tout type d’étude dynamique.

Amortissement de Rayleigh

L’amortissement de Rayleigh est un moyen simple de générer une matrice d’amortissement sous la forme d’une combinaison linéaire pure des matrices de masse et de rigidité,

Ce modèle d’amortissement n’a pas de lien direct avec les processus d’amortissement physiques. Initialement, il a été introduit parce qu’il donne une matrice diagonalisable par les modes propres associés aux fréquences propres non amorties, ce qui permet d’obtenir un découplage dynamique complet entre les différents modes.

Le terme de la matrice de rigidité (“amortissement bêta”) peut, cependant, être interprété comme étant directement proportionnel à la vitesse de déformation. En réalité, un amortissement bêta pur correspond à un amortissement visqueux avec

Où K et G sont respectivement les modules d’élasticité et de cisaillement.

L’amortissement bêta, tout comme l’amortissement visqueux, fournit un amortissement qui est plus important aux fréquences élevées. A contrario, le terme α proportionnel à la masse, fournit un amortissement qui est plus important aux basses fréquences. Il agit sur la vitesse de la structure et amortit par conséquent les mouvements de corps rigide.

L’amortissement de Rayleigh est également disponible dans le sous-noeud Amortissement d’une loi de comportement. Cette fonctionnalité permet en effet de créer un type d’amortissement généralisé de l’amortissement de Rayleigh original. Pour que la matrice d’amortissement soit une combinaison linéaire des matrices de masse et d’amortissement au niveau du système d’équations, les paramètres de l’amortissement de Rayleigh doivent être les mêmes dans tous les noeuds Amortissement. Auquel cas, cette propriété n’est valide qu’à l’échelle d’un élément de maillage.

Vous pouvez renseigner les paramètres d’amortissement de Rayleigh de deux manières, soit en entrant directement α et β, soit en renseignant le taux d’amortissement à deux fréquences différentes.

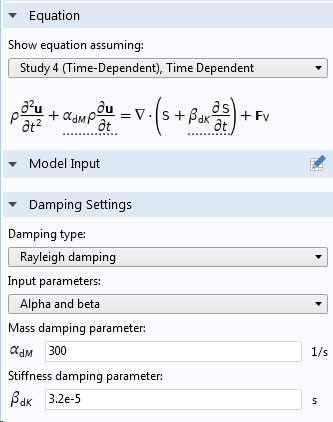
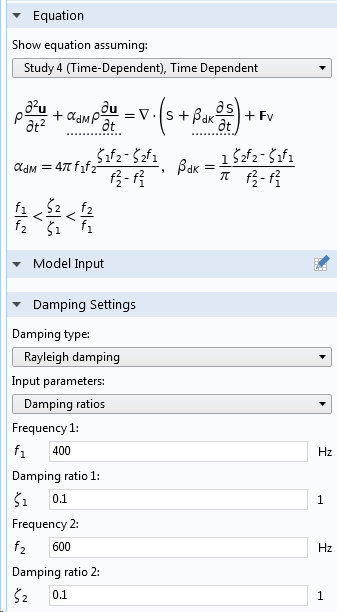
Saisie de l’amortissement de Rayleigh dans un sous-noeud Amortissement d’une loi de comportement.

Lois de comportement dissipatives

Certaines lois de comportement contiennent une dissipation inhérente. Dans ce contexte, le cas le plus intéressant est probablement celui de la viscoélasticité. Quand vous utilisez une telle loi de comportement, elle fournit généralement un amortissement important. Dans la plupart des cas, vous ne la combinerez pas avec un noeud Amortissement sur le même domaine géométrique.

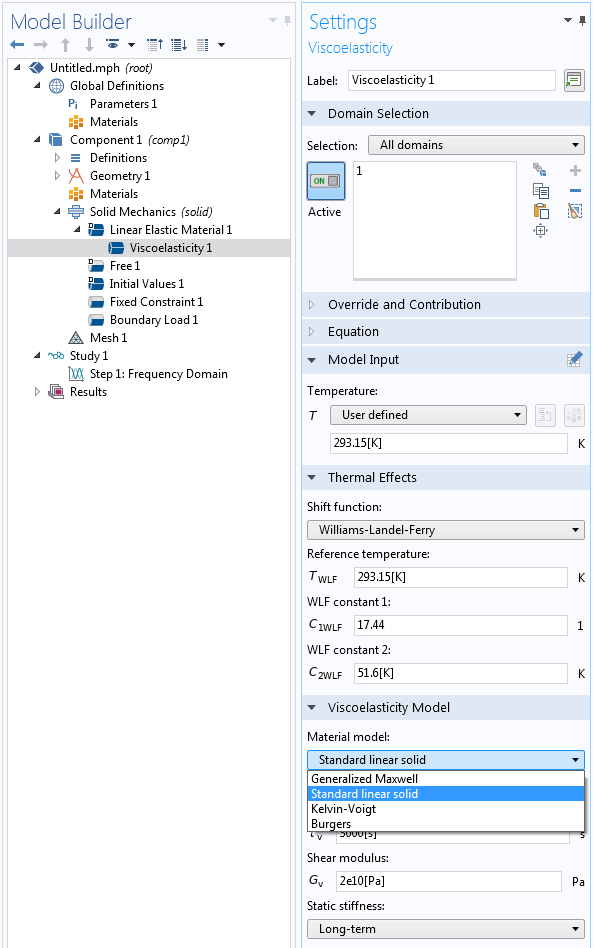
Sélection d’un matériau viscoélastique.

Amortissement thermoélastique

L’amortissement thermoélastique peut être directement incorporé dans un modèle grâce à un réglage du couplage multiphysique Dilatation thermique.

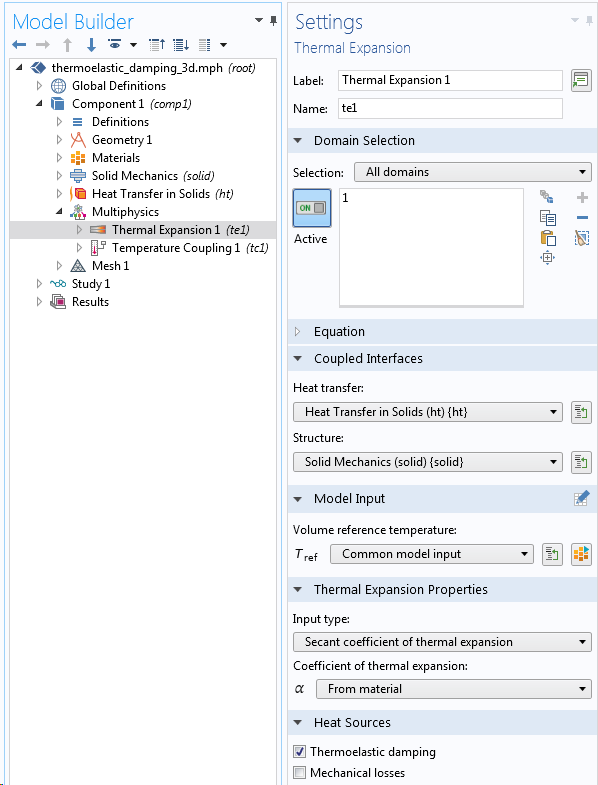
Amortissement thermoélastique dans une analyse couplée de transfert de chaleur et de dynamique des structures.

La prise en compte de l’amortissement thermoélastique a pour effet d’ajouter aux équations du bilan thermique un terme source de chaleur, proportionnel au taux de variation des contraintes,

Ici, T est la température, \boldsymbol \sigma est le tenseur des contraintes, et \boldsymbol \alpha est le tenseur coefficient de dilatation thermique.

Amortissement modal

La résolution des problèmes linéaires de dynamique des structures à l’aide de la superposition modale est une technique très efficace. Lorsque l’on utilise la superposition modale en même temps que l’amortissement, certains points sont à noter.

L’analyse initiale des fréquences propres doit être effectuée sans amortissement, et l’amortissement n’est ensuite inclus que lors de l’étape de superposition modale. La manière la plus pratique de s’en assurer est d’utiliser la section Sélection de la physique et des variables dans les réglages de chaque étape de l’étude.

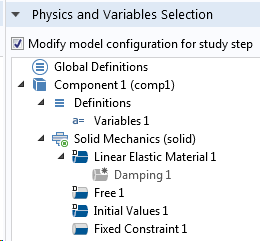
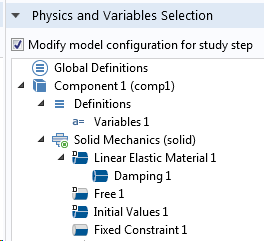
Réglages de l’étape de l’étude de fréquences propres (à gauche) et l’étude ultérieure de superposition modale (à droite).

Tous les types de contributions d’amortissement sont autorisés dans la superposition modale. Cela n’est peut-être pas surprenant, mais c’est dû au fait que les modes propres ne sont pas supposés être découplés par les solveurs modaux de COMSOL Multiphysics. Cela signifie que vous pouvez résoudre un éventail plus large de modèles avec amortissement par rapport à d’autres techniques de superposition modale.

En plus de l’amortissement fourni par diverses caractéristiques physiques, vous pouvez également fournir un taux d’amortissement pour chaque mode propre : c’est ce qu’on appelle l’Amortissement modal. L’amortissement modal est particulièrement utile si vous savez par expérience que certains modes sont plus fortement amortis que d’autres. C’est le cas lorsque différents phénomènes physiques sont liés aux déformées modales. L’amortissement modal est défini directement dans les réglages du solveur modal.

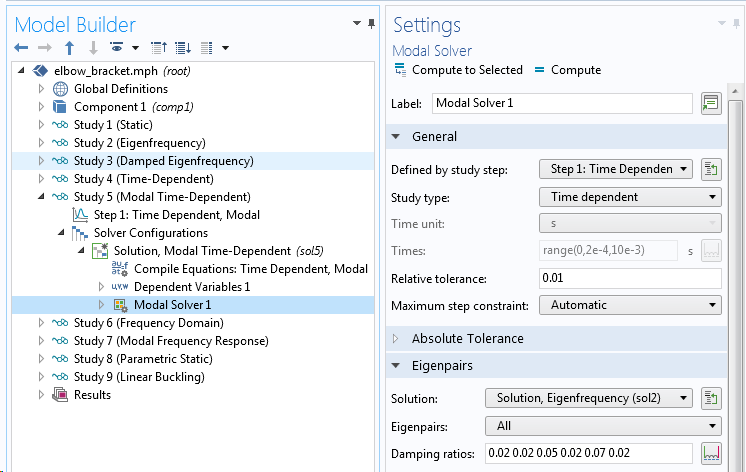
Saisie des réglages de l’amortissement modal.

L’amortissement modal est ajouté à toute autre contribution d’amortissement.

Conditions limites à l’infini

Lorsque vous devez modéliser des pertes d’émission acoustique ou des pertes d’ancrage, l’important est de munir votre modèle de conditions aux limites qui permettent aux ondes sortantes de disparaître sans phénomène de réflexion. COMSOL Multiphysics^® propose plusieurs options à cet égard, en fonction des interfaces physiques utilisées et du type d’analyse (domaine temporel ou domaine fréquentiel).

Dans le domaine fréquentiel, une couche parfaitement adaptée (PML) est une bonne alternative pour représenter une condition limite à “l’infini”. La formulation PML, qui est disponible pour de nombreuse interfaces physiques différentes, atténue essentiellement les ondes sortantes de manière à ce que l’énergie réfléchie soit très faible. Il en résulte que de l’amortissement sera présent dans l’analyse, puisque l’énergie des ondes sortantes est perdue.

Une PML est modélisée à l’aide de quelques couches d’éléments sur l’extérieur du domaine de calcul.

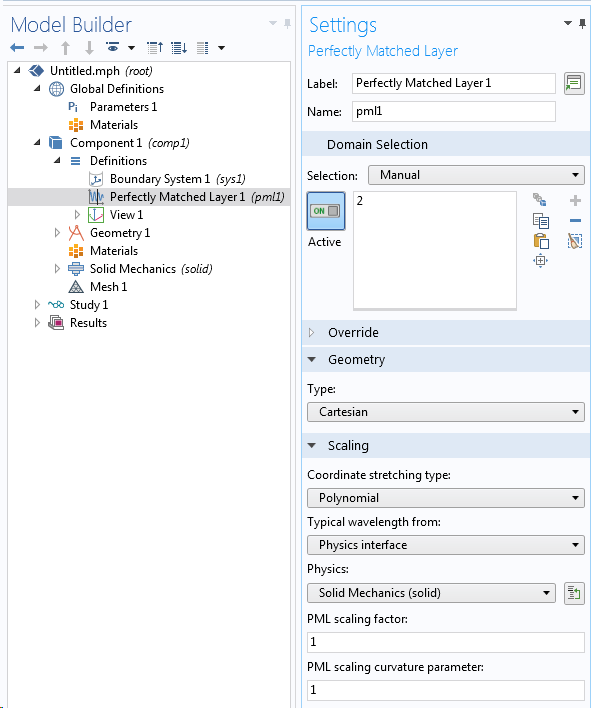
Définir un domaine en tant que PML.

Dans l’interface Mécanique du solide, vous pouvez également trouver un type particulier de condition limite appelé Frontière faiblement réfléchissante. Son rôle est le même que celui de la PML: éviter la réflexion des ondes. Bien qu’elle ne soit pas aussi efficace qu’une PML lorsque les ondes atteignent les frontières de manière oblique, le noeud Frontière faiblement réfléchissante présente deux avantages:

• Il peut être utilisé pour des analyses temporelles
• Comme il s’agit d’une condition limite, il n’est pas nécessaire de mailler des domaines supplémentaires en dehors du domaine de calcul

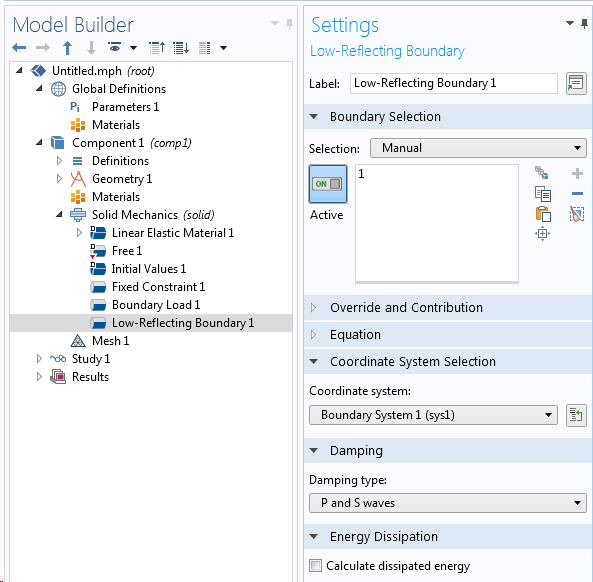
Le noeud Frontière faiblement réfléchissante.

Une autre manière de modéliser des ondes se propageant vers l’infini consiste à utiliser la méthode des éléments de frontière (BEM) formulée pour les ondes acoustiques.

Frottement entre surfaces

Si le frottement est une source importante d’amortissement, vous devrez souvent faire quelques approximations techniques. En principe, vous pouvez bien sûr résoudre un problème dépendant du temps avec une modélisation complète du contact, y compris avec du frottement. Malheureusement, dans la grande majorité des cas, le coût en termes de ressources de calcul sera excessif.

Une alternative consiste à remplacer la zone de contact par une couche mince élastique et à lui ajouter un amortissement visqueux ou un facteur de perte. Le problème consiste toutefois à estimer le module de cisaillement et le facteur de perte correspondant. Les méthodes générales d’estimation de ces paramètres font l’objet de recherches récentes et actives. Il se peut que vous deviez effectuer des analyses préalables du contact afin d’étudier ses propriétés.

L’amortissement avec d’autres fonctionnalités

Outre les lois de comportement, il existe de nombreuses autres fonctionnalités qui vous permettent d’intégrer de l’amortissement dans votre modèle. En voici quelques exemples :

• Fonctionnalité Attache par ressort
• Fonctionnalité Couche mince élastique
• Fonctionnalité Ressort-amortisseur
• Liaisons et engrenages dans l’interface Dynamique multicorps
• Les fonctionnalitésAmortisseur et Impédance dans l’interface Système mécanique discret
• Les paliers dans les interfaces Dynamique des rotors et Dynamique multicorps
• Tout chargement qui est exprimé en fonction de la vitesse
• Propriétés matériaux à valeurs complexes

Conclusion

La modélisation de l’amortissement en dynamique des structures est une partie essentielle et non triviale dans la mise en place du modèle. COMSOL Multiphysics vous offre un large éventail de fonctionnalités pour décrire l’amortissement. Obtenir des données correctes pour définir les matériaux et les composants d’une structure est cependant souvent difficile.

Etapes suivantes

Découvrez le module Structural Mechanics, qui comprend des caractéristiques et des fonctionnalités spécifiques pour la modélisation de l’amortissement :

• Lisez la partie 1 de cette série d’articles de blog: L’amortissement en dynamique des structures : théorie et phénomènes sources
• Si vous êtes intéressé par la modélisation de l’amortissement, vous trouverez plusieurs exemples illustrant différentes approches dans la bibliothèque d’applications :
  • Static and Eigenfrequency Analyses of an Elbow Bracket
  • Viscoelastic Structural Damper — Transient Analysis
  • Bracket — Transient Analysis (bracket_frequency.mph)
  • Wave Propagation in Rock Under Blast Loads
  • Piezoelectric Tonpilz Transducer
  • Thermoelastic Damping in a MEMS Resonator
  • Disc Resonator Anchor Losses
  • Vibrating Micromirror with Viscous and Thermal Damping: Transient Behavior