Centre d'apprentissage

Creating a Polynomial Chaos Expansion Surrogate Model from Imported Data

---

To continue the process of learning how to create surrogate models in COMSOL^® using imported data, we will now walk through fitting imported data to a Polynomial Chaos Expansion (PCE) surrogate mode. We will use the same dataset that we used in Part 5. This dataset takes the form of a functional surface, and the variables can represent any quantity. The workflow presented here is applicable when the data originates from experimental results.

Note: The Uncertainty Quantification Module is required for this example.

Polynomial Chaos Expansion Overview and Comparison to Gaussian Process Model

PCE surrogate models are widely used for uncertainty quantification (UQ), particularly in sensitivity analyses. They serve as a valuable alternative to Gaussian Process (GP) surrogate models, as they do not require hyperparameter optimization or the selection of a covariance function. Instead, PCE involves selecting a predefined probability distribution for each input parameter. Based on these distributions, the method automatically determines an appropriate polynomial basis and expands the quantities of interest within that basis, known as a polynomial chaos expansion. This approach is particularly efficient for sensitivity analyses, as implemented in the Uncertainty Quantification Module, for identifying the most influential quantities of interest. Subsequently, a GP model can be used for more detailed analyses, such as uncertainty propagation or localized standard deviation estimates, focusing on the most influential parameters identified.

Here, we will learn how to create a PCE model. Unlike GP models, a PCE model does not provide pointwise uncertainty. However, using the Uncertainty Quantification Module, we can compute statistical metrics such as the global mean and variance of the surrogate model. For an example of a sensitivity analysis based on a PCE model, see the next part of this course: "Sensitivity Analysis Using a Polynomial Chaos Expansion Surrogate Model".

Fitting Imported Data with a PCE Surrogate Model

Start by loading the GP surrogate model with UQ (gp_experimental_fit_uq.mph) from Part 5. We will continue working on this model, which has the training data stored in the Table 1 node.

The training data for this example is stored in Table 1.

First, rename the model to pce_experimental_fit_uq.mph and save.

If you have access to the Uncertainty Quantification Module, you can now add a Polynomial Chaos Expansion surrogate model function. To do this, right-click Global Definitions and select Polynomial Chaos Expansion from the Functions menu.

Adding a Polynomial Chaos Expansion surrogate model.

In the Polynomial Chaos Expansion function Settings window, choose Result table as the Data source and then select Table 1 for the Result table setting. The Data Column Settings section will automatically be filled out with default Argument and Function values: x1, x2, and pce1.

The settings for the Polynomial Chaos Expansion surrogate model function.

In this case, we will assume that the two input parameters have a uniform distribution in . Click the first row in the Data Column Settings table and type 0 and 10 for the Lower bound and Upper bound, respectively. Repeat this process for the second row.

The uniform distribution settings for the input parameters.

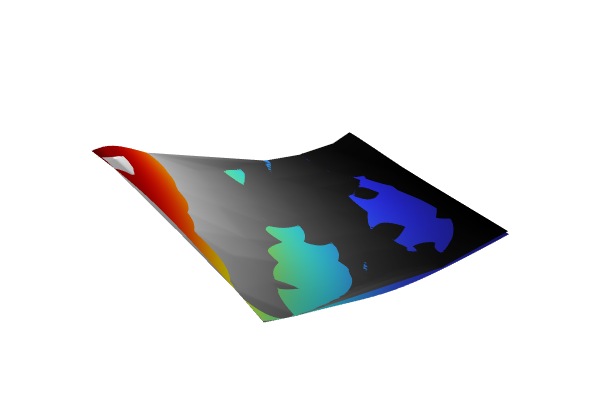
At the top of the Polynomial Chaos Expansion function Settings window, click Train Model. In this case, this action prompts a warning message that 116 of the 900 training points are excluded. The reason for this is that 116 of the training points are on the boundary of the rectangle . The Legendre polynomial approximation algorithm cannot handle this; it is required that we extend the domain slightly.

The PCE method gives a warning for data lying exactly on the boundary.

We can extend the domain slightly by introducing a parameter with a small value. Under the Parameters 1 node, enter a new parameter with the name small and the expression 1e-6.

The global parameter for extending the surrogate model region.

Now modify the bounds of the uniform distribution by changing the Lower bound and Upper bound values to 0-small (or just -small) and 10+small, respectively, for both input parameters.

The extended bounds for the uniform distribution.

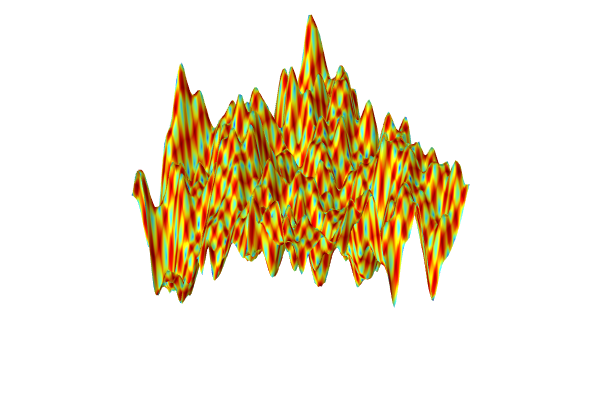
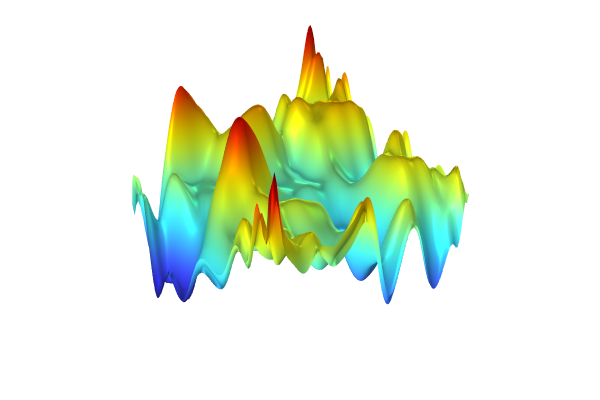
To generate the surrogate model, click Train Model at the top of the Polynomial Chaos Expansion function Settings window. The computation takes a few seconds. Once it is complete, plot the function by clicking the Create Plot button. The plot can be seen in the figure below.

The Model Builder with the Function 1 plot node selected and the corresponding Settings window and plot visualization displayed.

A visualization of the Polynomial Chaos Expansion surrogate model created from experimental data.

The dataset appears to vary wildly. However, this is due to the automatic z-axis scaling, and upon further inspection, the function values are within a narrow range between about 1.15 and 1.24.

We are now interested in computing the global mean value and standard deviation. To do this, we need to run the Uncertainty Quantification study. The study currently uses the previously computed GP model, which we will now change to the PCE model.

Computing Uncertainty with the Uncertainty Quantification Study

In the Uncertainty Quantification study Settings window, change the Surrogate model setting to Sparse polynomial chaos expansion. Then, change the PCE function to the one we just trained: Polynomial Chaos Expansion (pce1). Finally, change the option for the Compute action setting to Analyze only. This option enables us to compute statistical properties without retraining the surrogate model.

The Uncertainty Quantification study Settings window, showing the settings for the PCE function.

The default surrogate model for Sensitivity is Adaptive Sparse polynomial chaos expansion. However, in this case, we will reuse an existing surrogate model, so the adaptive method will not be invoked. The adaptive method requires the generation of new data points, which is not possible for imported data since there is no finite element model to compute additional data points. Therefore, when we select the Analyze only option, the adaptive method is automatically disengaged, and there is no need to change this setting. In this example, both the Adaptive sparse polynomial chaos expansion and the Sparse polynomial chaos expansion settings use a nonadaptive PCE method.

Now we are ready to analyze the surrogate model. At the top of the Uncertainty Quantification window, click Compute. Recall that in the case of an Uncertainty Quantification study, the sampled variables are output to a Quantities of Interest table, rather than a Design Data table.

When the computation is finished, a Kernel Density Estimation (KDE) plot is shown. Recall that a KDE plot is a smoothed histogram plot and represents the probability density function estimate for the function value considering all input values in the region . In other words, the KDE plot shows the most probable function values when the input parameter space is randomly uniformly sampled within the set parameter boundaries.

A KDE plot showing the probability density function estimate for the function values of the imported data.

We can also get statistical information from this computation. If not already visible, under the Results > Tables node, select the QoI Confidence Interval table under Uncertainty Propagation.

Selecting the QoI Confidence Interval table.

The QoI Confidence Interval table contains information about the surrogate model's global mean and standard deviation as well as the minimum, maximum, and various quantile values.

The QoI Confidence Interval table.

The global mean value is computed to about 1.2 and the standard deviation is about 0.013, indicating a near constant dataset. The minimum and maximum values are about 1.15 and 1.24, respectively. Note that these values do not correspond to the original dataset but to the fitted surrogate model function. Furthermore, notice that the computed statistical values are consistent with that of the GP model in Part 5, despite this PCE model being at a coarser level of approximation.