The KdV Equation and Solitons
Application ID: 85
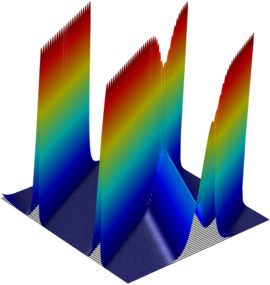
The Korteweg-de Vries (KdV) equation models water waves. It contrasts sharply to the Burgers equation, because it introduces no dissipation and the waves travel seemingly forever. Solitons have their primary practical application in optical fibers. Specifically, a fiber’s linear dispersion properties level out a wave while the nonlinear properties give a focusing effect. The result is a very stable, long-lived pulse. This solution says that the pulse’s speed determines its amplitude and width. This simulation illustrates this effect.
This model example illustrates applications of this type that would nominally be built using the following products:
however, additional products may be required to completely define and model it. Furthermore, this example may also be defined and modeled using components from the following product combinations:
The combination of COMSOL® products required to model your application depends on several factors and may include boundary conditions, material properties, physics interfaces, and part libraries. Particular functionality may be common to several products. To determine the right combination of products for your modeling needs, review the Grille des Spécifications and make use of a free evaluation license. The COMSOL Sales and Support teams are available for answering any questions you may have regarding this.
