Menu

Discussion Forum

New Discussion
Filtrer

Validating Biot Savart law

Posted 23 janv. 2025, 08:10 UTC−5 Electromagnetics Version 6.2 3 Replies

Navaneeth M N
Send Private Message Flag post as spam

Please login with a confirmed email address before reporting spam

I am attempting to validate the magnetic flux density value from theoretical calculations to COMSOL modeling.

I have calculated the magnetic field intensity at a point located at the midpoint of a finite 1-meter wire carrying 1A current, positioned 1 meter away from the wire, which amounts to 8.9 × 10^-8 Tesla (T).

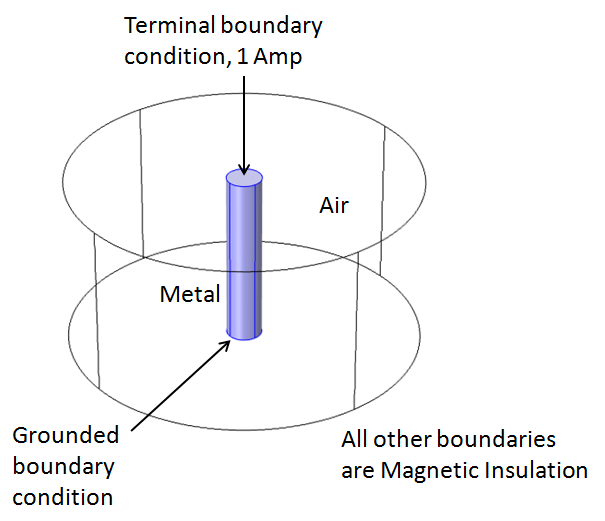
I am modeling this using COMSOL's 3D AC/DC interface and have created the geometry as described. The central cylindrical structure represents the current-carrying wire, and the surrounding cylindrical enclosure is an air boundary. I have specified a wire thickness of 0.05 meters and assigned copper as the material. The boundary structure is assigned air properties. I have created a point inside the air cylindrical surface exactly 1 meter away from the midpoint of the current-carrying wire. I am studying the magnetic flux density (B) in tesla (T). However, I am obtaining a value of 2 × 10^-7 T, which does not match my calculated value.

I would appreciate suggestions on what might be causing this discrepancy.

If possible, could you provide more details about your theoretical calculation method and the specific COMSOL settings you've used?

Regards,

Navaneeth

image:

Reply
3 Replies Last Post 25 janv. 2025, 14:36 UTC−5
Robert Koslover Certified Consultant
Send Private Message Flag post as spam

Please login with a confirmed email address before reporting spam

Posted: 2 days ago 23 janv. 2025, 20:28 UTC−5
Updated: 2 days ago 23 janv. 2025, 20:31 UTC−5

Hmm. Just for fun, I created a model that looks much like yours. I also get 2x10^-7 T at 1m from the center of the wire. But there is an important difference . And that is that I also separately computed the field analytically using Ampere's law, which simply predicts that B will be . Plug in the numbers and, Lo and Behold, Ampere's law predicts 2x10^-7 T. So, Comsol Multiphysics and the laws of physics agree!

Heh. Of course, you didn't mention Ampere's law. Rather, you mentioned the law of Biot and Savart. That would normally be used for computing a contribution to B from a finite length of current carrying wire. But the typical default boundary conditions (e.g., if using the mf interface) in Comsol Multiphysics will be magnetic insulation, which leads to conditions that nicely match an infinitely long wire. So, I'm guessing you simply accepted the default boundary conditions, right? If you instead use the law of Biot and Savart to compute the field from an infinitely long wire, I expect you will find same result as from Ampere's law. QED.

-------------------
Scientific Applications & Research Associates (SARA) Inc.
www.comsol.com/partners-consultants/certified-consultants/sara
Hmm. Just for fun, I created a model that looks much like yours. I also get 2x10^-7 T at 1m from the center of the wire. But there is an *important difference* . And that is that I also separately computed the field analytically using Ampere's law, which simply predicts that B will be \mu_{0}I/(2\pi R). Plug in the numbers and, Lo and Behold, Ampere's law predicts 2x10^-7 T. So, Comsol Multiphysics and the laws of physics agree! Heh. Of course, *you didn't mention Ampere's law*. Rather, you mentioned the law of Biot and Savart. That would normally be used for computing a *contribution* to B from a *finite length* of current carrying wire. But the typical default boundary conditions (e.g., if using the mf interface) in Comsol Multiphysics will be magnetic insulation, which leads to conditions that nicely match an infinitely long wire. So, I'm guessing you simply accepted the default boundary conditions, right? If you instead use the law of Biot and Savart to compute the field from an *infinitely long* wire, I expect you will find same result as from Ampere's law. QED.
Navaneeth M N
Send Private Message Flag post as spam

Please login with a confirmed email address before reporting spam

Posted: 1 day ago 25 janv. 2025, 01:04 UTC−5
Updated: 1 day ago 25 janv. 2025, 01:10 UTC−5

Hmm. Just for fun, I created a model that looks much like yours. I also get 2x10^-7 T at 1m from the center of the wire. But there is an important difference . And that is that I also separately computed the field analytically using Ampere's law, which simply predicts that B will be \mu_{0}I/(2\pi R). Plug in the numbers and, Lo and Behold, Ampere's law predicts 2x10^-7 T. So, Comsol Multiphysics and the laws of physics agree!

Heh. Of course, you didn't mention Ampere's law. Rather, you mentioned the law of Biot and Savart. That would normally be used for computing a contribution to B from a finite length of current carrying wire. But the typical default boundary conditions (e.g., if using the mf interface) in Comsol Multiphysics will be magnetic insulation, which leads to conditions that nicely match an infinitely long wire. So, I'm guessing you simply accepted the default boundary conditions, right? If you instead use the law of Biot and Savart to compute the field from an infinitely long wire, I expect you will find same result as from Ampere's law. QED.

Thank you for your detailed response! You’re absolutely right that the result for an infinite conductor aligns perfectly with Ampere's law, which predicts . It’s great to see that both COMSOL and the analytical solution agree, confirming the physics.

As you noted, my original focus was on the finite wire scenario, where the magnetic field is described by the equation:

I understand now that the default magnetic insulation boundary conditions in COMSOL are more suited for modeling infinite wires, which is why my results aligned with Ampere's law rather than the Biot-Savart law for finite wires. I suspect that modifying these boundary conditions or explicitly defining the finite length of the wire in the geometry might bring the results closer to the finite wire equation.

Could you share any insights or specific suggestions on how to tweak these boundary conditions or the setup in COMSOL to accurately model a finite wire? As I’m still getting the hang of COMSOL, any pointers would be greatly appreciated!

Thank you again for your explanation, it’s been very helpful in clarifying the key differences between the two approaches.

>Hmm. Just for fun, I created a model that looks much like yours. I also get 2x10^-7 T at 1m from the center of the wire. But there is an *important difference* . And that is that I also separately computed the field analytically using Ampere's law, which simply predicts that B will be \mu_{0}I/(2\pi R). Plug in the numbers and, Lo and Behold, Ampere's law predicts 2x10^-7 T. So, Comsol Multiphysics and the laws of physics agree! > >Heh. Of course, *you didn't mention Ampere's law*. Rather, you mentioned the law of Biot and Savart. That would normally be used for computing a *contribution* to B from a *finite length* of current carrying wire. But the typical default boundary conditions (e.g., if using the mf interface) in Comsol Multiphysics will be magnetic insulation, which leads to conditions that nicely match an infinitely long wire. So, I'm guessing you simply accepted the default boundary conditions, right? If you instead use the law of Biot and Savart to compute the field from an *infinitely long* wire, I expect you will find same result as from Ampere's law. QED. Thank you for your detailed response! You’re absolutely right that the result for an infinite conductor aligns perfectly with Ampere's law, which predicts \mu_{0}I/(2\pi R). It’s great to see that both COMSOL and the analytical solution agree, confirming the physics. As you noted, my original focus was on the finite wire scenario, where the magnetic field is described by the equation: \mu_{0}I/(4\pi R) * (sin\theta_{2} - sin\theta_{1}) I understand now that the default magnetic insulation boundary conditions in COMSOL are more suited for modeling infinite wires, which is why my results aligned with Ampere's law rather than the Biot-Savart law for finite wires. I suspect that modifying these boundary conditions or explicitly defining the finite length of the wire in the geometry might bring the results closer to the finite wire equation. Could you share any insights or specific suggestions on how to tweak these boundary conditions or the setup in COMSOL to accurately model a finite wire? As I’m still getting the hang of COMSOL, any pointers would be greatly appreciated! Thank you again for your explanation, it’s been very helpful in clarifying the key differences between the two approaches.
Robert Koslover Certified Consultant
Send Private Message Flag post as spam

Please login with a confirmed email address before reporting spam

Posted: 11 hours ago 25 janv. 2025, 14:36 UTC−5
Updated: 11 hours ago 25 janv. 2025, 14:41 UTC−5

You're welcome. An isolated DC current segment does not represent a physically-realizable system. That said, use of the Biot Savart law is still valid in the "real world" so long as you apply it to a closed circuit. Now, the contribution of a section of a wire to an overall field may be of interest and, in general cases other than straight segments, not have an obvious analytic solution (although you could certainly write down the integral expression). If you already know what the current is along a curve (or wire), then all you need is to do the integral. You don't really need Comsol Multphysics for that. But in principle, you could still set it up in a Comsol Multiphysics environment, and then (in the case of a 1D curve) define an appropriate post-processing line-integral operation to compute the field contribution explicitly using the Biot Savart law. This approach would be (from my perspective) magnetostatically analoguous to that described in https://www.comsol.com/community/exchange/672/ , since you would need to use an integration coupling variable and the dest operator. But in your case, the equations would be simpler, since you'd be doing a line integral instead of a surface integral (unless your wire is so thick that you are concerned about that distinction, in which case you might even need a volumetric integral involving J along the wire) but at least there wouldn't be a phase term, since the current is steady (unless you vary it!). I don't know if that helps. Regards,

-------------------
Scientific Applications & Research Associates (SARA) Inc.
www.comsol.com/partners-consultants/certified-consultants/sara
You're welcome. An isolated DC current segment does not represent a physically-realizable system. That said, use of the Biot Savart law is still valid in the "real world" so long as you apply it to a closed circuit. Now, the *contribution* of a *section* of a wire to an overall field may be of interest and, in general cases other than straight segments, not have an obvious analytic solution (although you could certainly write down the integral expression). If you already know what the current is along a curve (or wire), then all you need is to do the integral. You don't really need Comsol Multphysics for that. But in principle, you could still set it up in a Comsol Multiphysics environment, and then (in the case of a 1D curve) define an appropriate post-processing line-integral operation to compute the field contribution explicitly using the Biot Savart law. This approach would be (from my perspective) magnetostatically analoguous to that described in https://www.comsol.com/community/exchange/672/ , since you would need to use an integration coupling variable and the dest operator. But in your case, the equations would be simpler, since you'd be doing a line integral instead of a surface integral (unless your wire is so thick that you are concerned about that distinction, in which case you might even need a volumetric integral involving J along the wire) but at least there wouldn't be a phase term, since the current is steady (unless you vary it!). I don't know if that helps. Regards,

Reply

Please read the discussion forum rules before posting.

Please log in to post a reply.

Note that while COMSOL employees may participate in the discussion forum, COMSOL® software users who are on-subscription should submit their questions via the Support Center for a more comprehensive response from the Technical Support team.

Suggested Content