
Simulation des accéléromètres et des gyroscopes MEMS utilisés dans les unités de mesure inertielle
De nos jours, la plupart des gens ne partent pas en voyage sans un appareil de navigation connecté au système de positionnement mondial (GPS : Global Positioning System). Mais les signaux GPS peuvent être interrompus lorsqu’un véhicule passe sous terre ou entre de grands immeubles. C’est pourquoi de nombreux véhicules, téléphones mobiles et autres appareils sont équipés d’unités de mesure inertielle, ou IMU. Une IMU utilise des gyroscopes et des accéléromètres incroyablement petits et précis pour déterminer un mouvement par rapport à des axes orthogonaux de la Terre. Les composants d’une IMU, y compris les gyroscopes et les accéléromètres MEMS, sont modélisables avec le logiciel COMSOL Multiphysics®.
Quand “Vous êtes ici” rejoint “Côté haut”
Imaginez un ciel d’un noir profond, dont l’obscurité est éclaircie par des milliers de points blancs, formant ce qui se révèle être la Voie lactée. Et au-dessus de notre galaxie, une flèche pointe vers l’un des petits points, avec un texte pas très utile indiquant “VOUS ÊTES ICI”.

Exemple d’un instrument de navigation avec un système de référence.
Cette vieille plaisanterie visuelle, qui a peut-être figuré sur autant de T-shirts passionés et de portes de professeurs qu’il y a d’étoiles dans le ciel, laisse entrevoir certaines vérités sur l’aspect relativiste de la navigation (et de la vie !). Sa principale leçon est peut-être de nous dire que l’emplacement d’un objet ne peut être décrit de façon utile que par rapport à l’espace qui l’entoure. En navigation, cet espace est le système de référence.
Lorsque nous traçons notre route sur une carte routière, nous naviguons dans un référentiel bidimensionnel. Une carte seule ne peut pas nous dire si nous montons ou descendons une côte, ou si notre véhicule risque de se retourner. Un système de navigation équipé d’une IMU peut calculer la trajectoire d’un véhicule dans un espace tridimensionnel en mesurant l’accélération linéaire et angulaire. Avec trois accéléromètres orientés selon les axes x-, y-, ou z, nous pouvons mesurer les rotations dans un espace 3D. (Ref. 1)
Des pierres à l’intérieur de votre tête ? Elles font partie de vos accéléromètres
Si vous agissez de façon inadaptée, on vous demandera peut-être : “Avez-vous des caillous dans la tête ? Si cela se produit, vous pouvez répondre honnêtement que oui, nous en avons tous, et même les plus fous devraient savoir qu’ils sont très importants ! Le corps de chaque vertébré contient de microscopiques otolithes composés principalement de carbonate de calcium — l’ingrédient principal du calcaire. (Otolithe en grecque pour “pierre d’oreille”.) Ces pierres dans notre tête font partie intégrante des accéléromètres naturels de notre corps. (Ref. 2)
Un accéléromètre consiste en une masse libre, suspendue à une structure flexible fixée à un boîtier. Lorsque le boîtier subit une accélération, la masse libre en fait autant, produisant une tension mesurable sur la suspension. Dans le cas des accéléromètres situés dans nos oreilles, la masse libre est un ensemble d’otolithes. Cet ensemble est attaché à une membrane suspendue à des poils microscopiques et à des nerfs qui détectent les variations électriques lorsque la masse se déplace. Cet accéléromètre organique est relié à la structure de notre oreille interne, qui sert de système de référence.
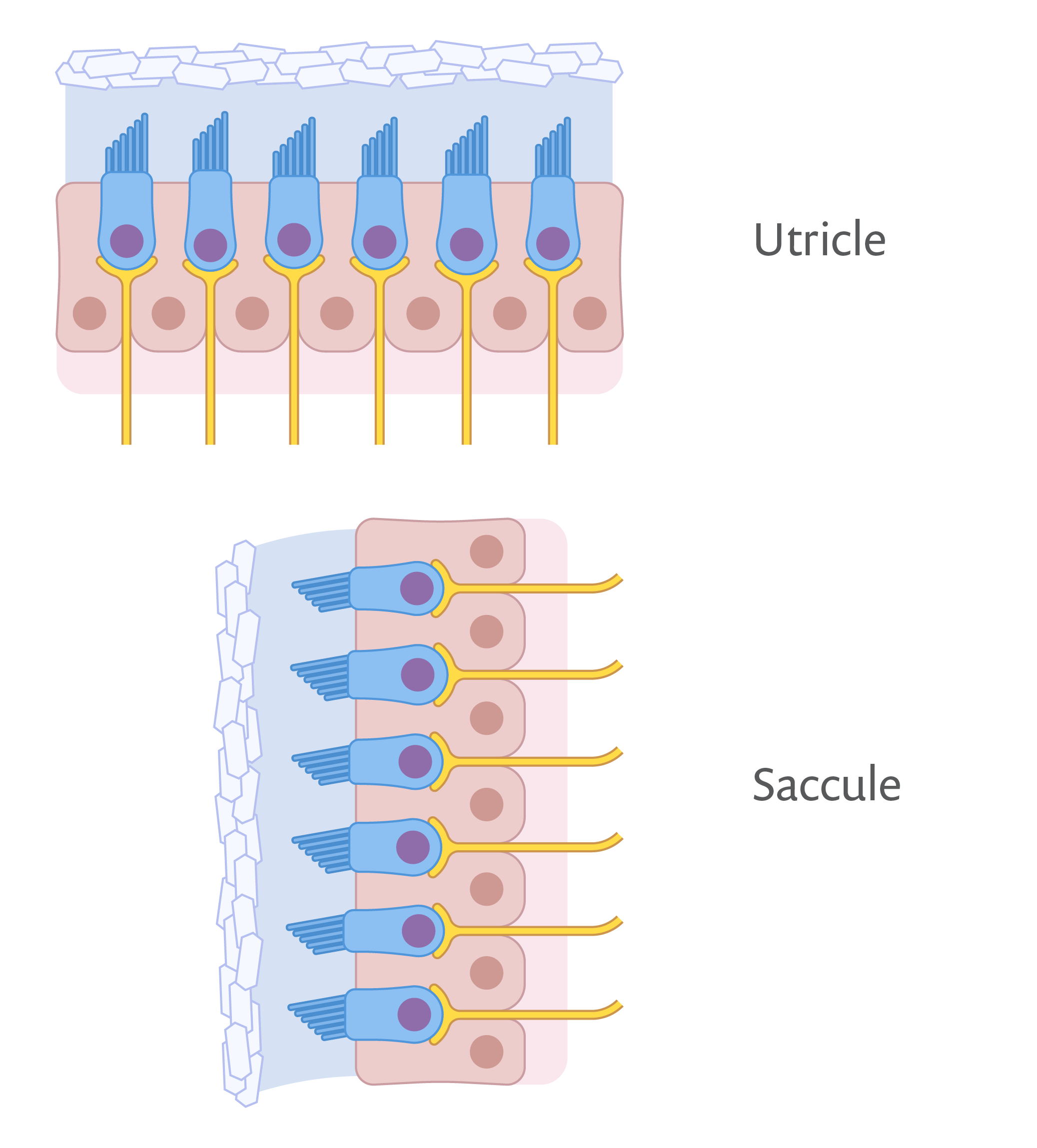
Le corps humain contient un utricule placé horizontalement et un saccule vertical dans chaque oreille. Chacune de ces structures microscopiques contient une masse libre suspendue qui stimule les nerfs qui y sont attachés, en réponse à une accélération. (Ref. 3)
Lorsque notre corps se déplace brusquement, le déplacement de la masse libre avertit nos nerfs du risque potentiel de chute. Nos nerfs peuvent ainsi détecter les mouvements de notre corps même lorsque d’autres organes sensoriels, comme nos yeux ou nos oreilles, perdent la trace de leur système de référence. Les accéléromètres micro-usinés en surface jouent un rôle similaire pour les appareils et les véhicules.
“Construction par blocs” pour modéliser un accéléromètre MEMS
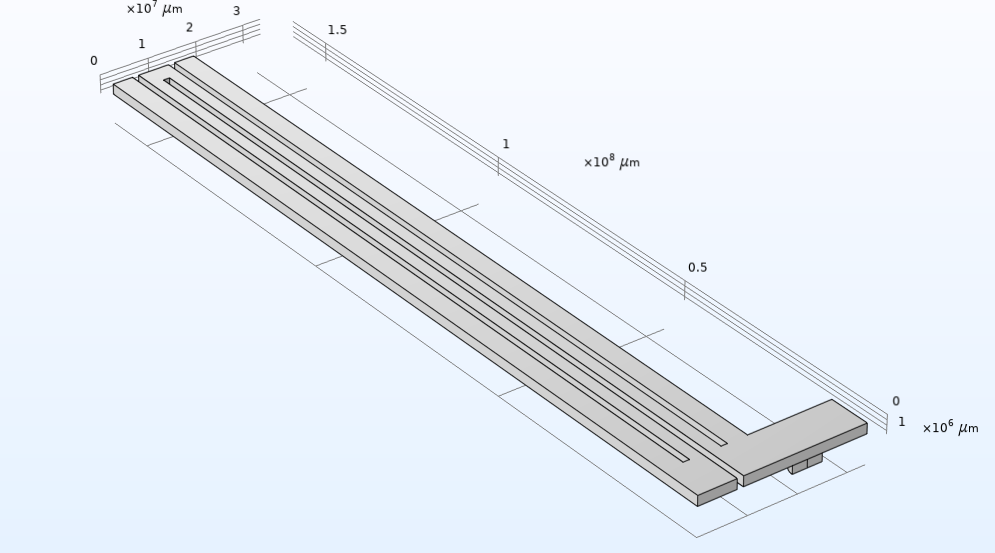
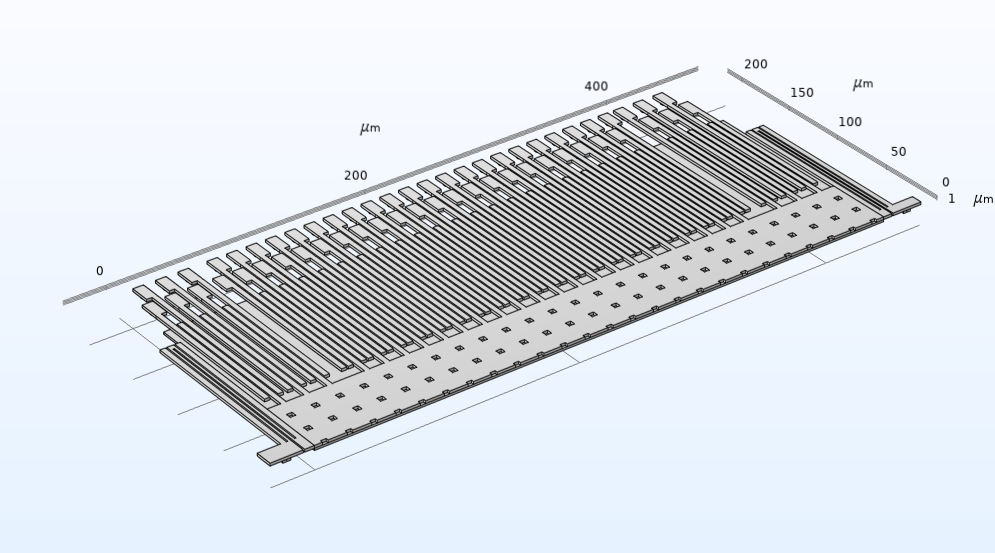
Le modèle tutoriel présenté ici montre comment modéliser un accéléromètre micro-usiné en surface à l’aide de l’interface multiphysique Electromécanique du module MEMS. Le modèle se compose de trois sous-ensembles : la masse libre, les ressorts fixés qui soutiennent cette masse et le réseau d’électrodes. Parcourez le diaporama pour voir les trois sous-ensembles ainsi que le modèle complet.
Lorsque l’appareil subit une accélération, la masse libre se déplace, ce qui fait varier la capacité entre les électrodes fixes et mobiles. Cette variation de la capacité est proportionnelle à l’accélération.
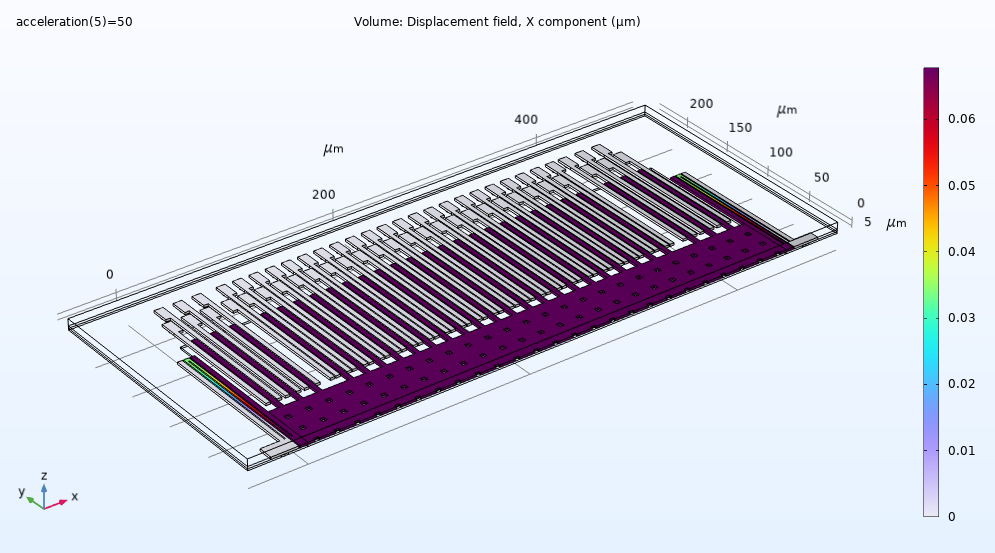
Déplacements obtenus pour une accélération imposée de 50 g. Avec cette sollicitation, la masse libre se déplace d’environ 0.07 micromètre.
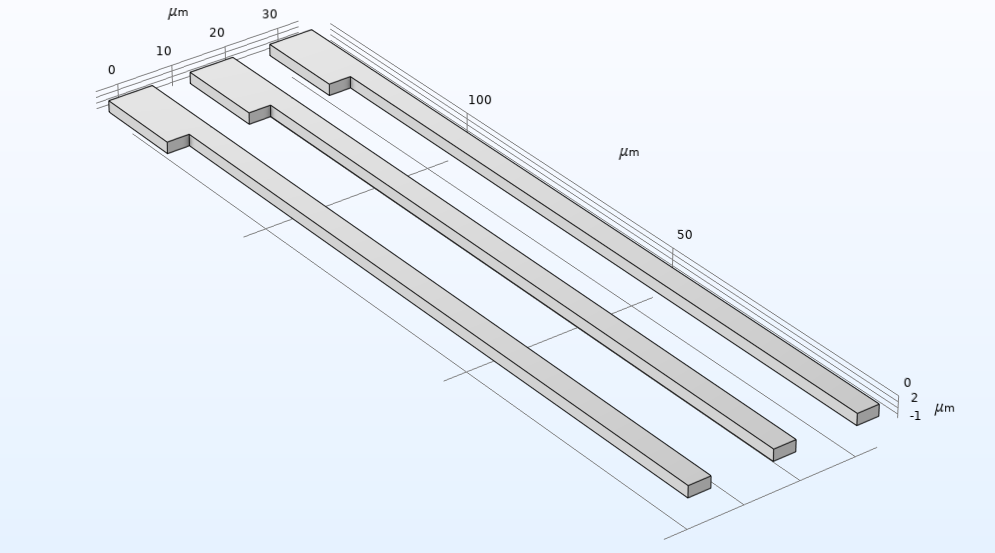
Lors de la définition du modèle, vous pouvez spécifier les dimensions, l’orientation et d’autres propriétés pour les trois composants de base que sont la masse libre, les ressorts et les électrodes. Vous pouvez tester différentes configurations de conception en ajustant les valeurs des paramètres clés pour ces blocs de construction modulaires également appelés sous-séquences. Cette modularité permet de prototyper et de tester les composants de l’accéléromètre et leurs configurations.
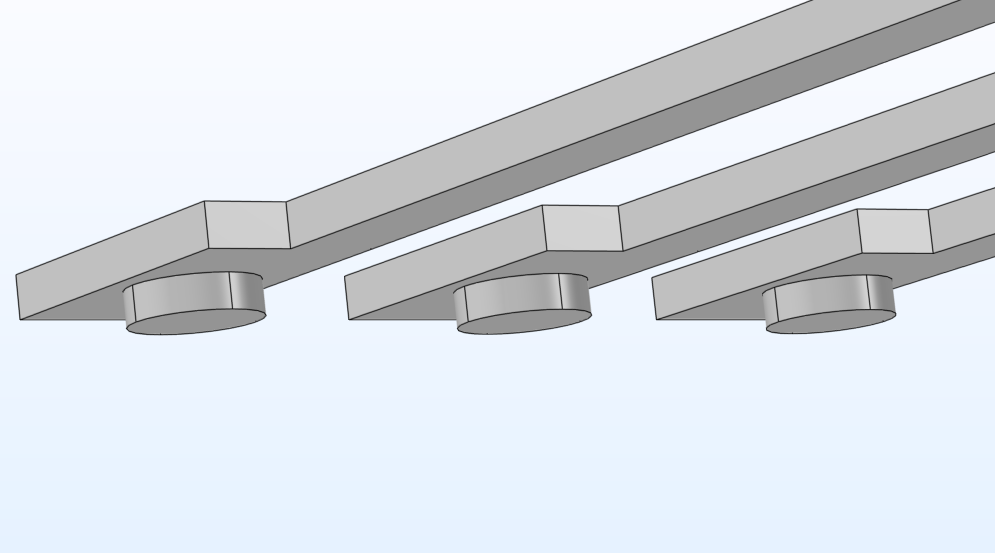
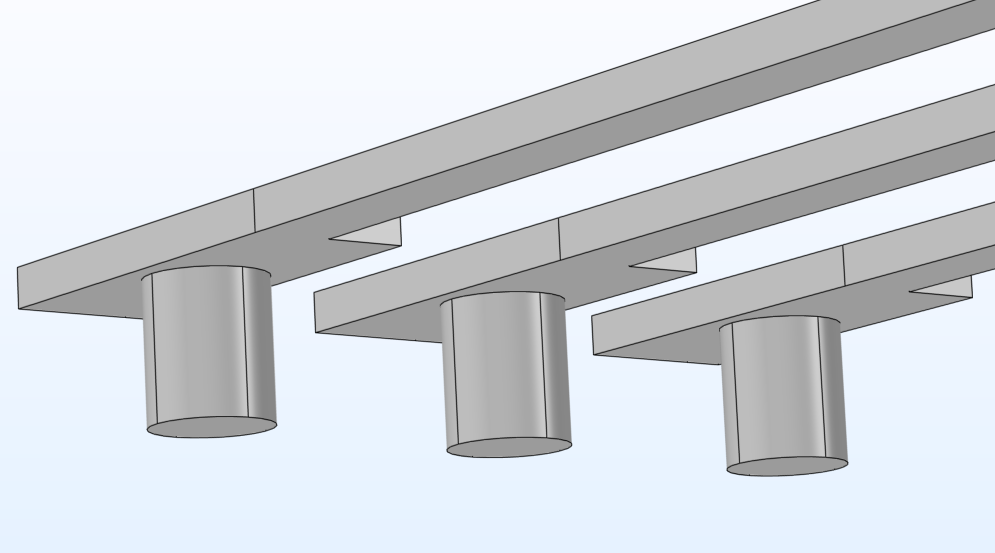
A gauche, un “bloc de construction” d’un réseau d’électrodes modulaire pour le modèle d’accéléromètre. Le réseau redessiné à droite a été conçu à partir de la même sous-séquence modulaire en ajustant les paramètres clés.
Hauts et bas des gyroscopes à diapason
Tout comme la nature a équipé certains animaux d’accéléromètres, d’autres ont leur propre gyroscope ! Les mouches domestiques, les moustiques et certains autres insectes volants possèdent deux appendices appelés haltères, que l’on peut voir derrière les ailes de cette tipule :

Vue du dessus d’une tipule, montrant la localisation de ses haltères. Imagine originale de Andre Vrijens, sous licence CC BY 3.0 via Wikimedia Commons.
L’haltère d’un insecte bat rapidement avec ses ailes. En vol horizontal, ce mouvement trace une trajectoire de haut en bas. Mais lorsque l’insecte incline son corps, la trajectoire des haltères se déplace en raison de l’effet Coriolis. Les haltères se déplacent alors de droite à gauche, mais aussi de haut en bas. L’insecte perçoit les mouvements de déplacement des haltères par la pression qu’ils exercent sur les poils qui y sont attachés. Cette information lui permet de contrôler son orientation par rapport à sa trajectoire de vol.
Un gyroscope piézoélectrique fonctionne selon des principes similaires. Explorons un modèle pour apprendre comment.
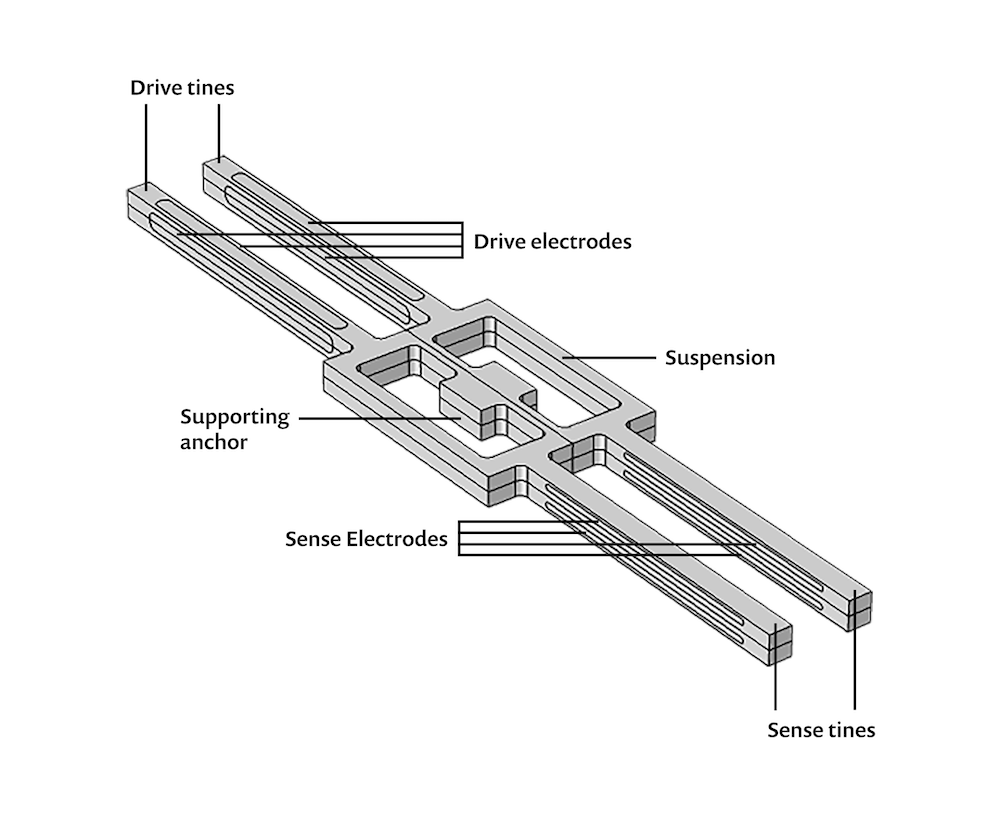
Schéma du modèle de gyroscope à diapason, montrant le plan de symétrie passant par le centre de l’appareil ainsi que les composants clés.
La forme rectangulaire au centre du gyroscope est sa suspension. L’ancrage de support de cet élément est fixé de manière rigide au dispositif dans lequel le gyroscope est installé. Les deux paires d’éléments en saillie sont les dents d’entraînement et les dents de détection. Des électrodes sur les deux paires de dents leur permettent de fournir des données utiles sur l’orientation du dispositif.
Pour expliquer comment cela fonctionne, considérons le comportement des dents lorsque le dispositif est soit immobile, soit en mouvement uniforme (sans accélération linéaire ou rotationnelle) par rapport à son système de référence. Nous verrons ensuite comment le comportement des dents change lorsque le dispositif est en rotation. Un signal électrique appliqué aux dents d’entraînement fait vibrer les dents sensorielles à leur fréquence de résonance dans le plan xy . Quand l’appareil est en rotation autour de l’axe y, la force de Coriolis résulte en des vibrations hors du plan, comme illustré ci-dessous.
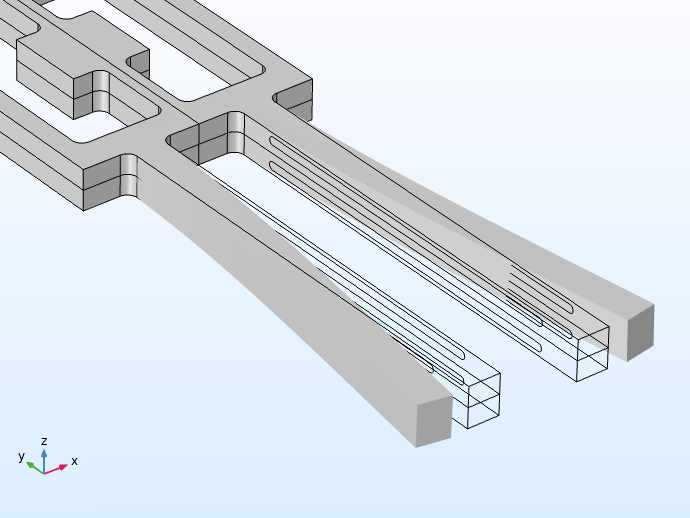
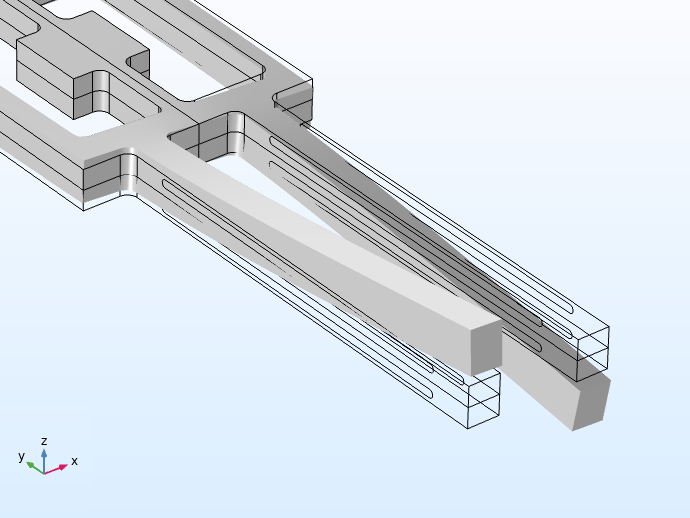
A gauche, l’application d’un courant alors que le dispositif est en mouvement uniforme fait vibrer les dents le long du plan xy . A droite, la rotation du dispositif par rapport à l’axe y provoque des vibrations perpendiculaires au plan selon l’axe z.
Notez que les tiges d’entraînement et les tiges de détection ont des fréquences de résonance différentes. Lorsque le gyroscope fonctionne, les électrodes situées aux tiges de commande les font vibrer à leur fréquence de résonance par effet piézoélectrique inverse. Lorsque l’appareil entier est en rotation autour de l’axe y, la force de Coriolis résultante fait vibrer les tiges de détection hors du plan, et ce mouvement génère du courant dans les électrodes des tiges de détection par effet piézoélectrique direct.
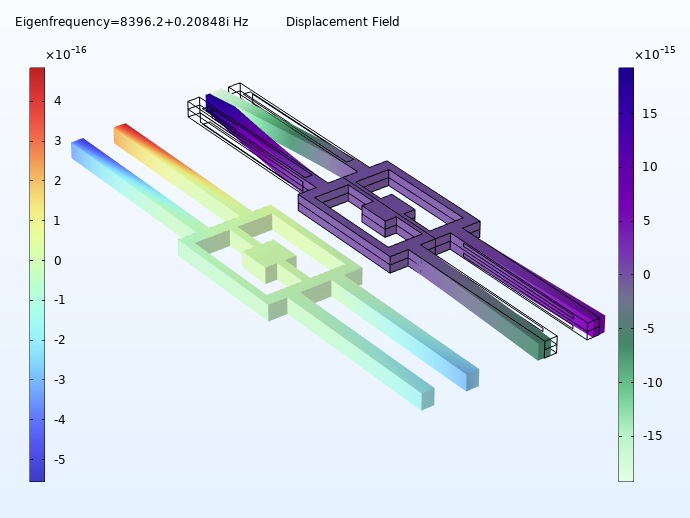
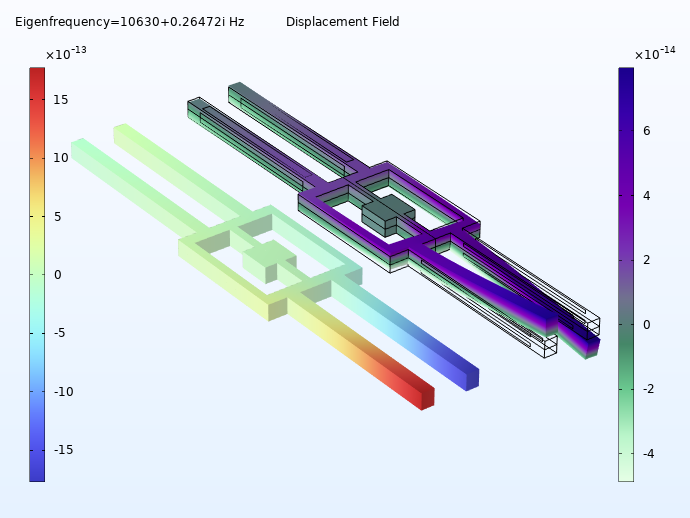
L’image de gauche montre deux graphiques du dispositif en mouvement uniforme, sans accélération ni rotation. Notez que les tiges vibrent dans le plan xy . A droite, l’appareil est en rotation autour de l’axe y, ce qui fait vibrer les tiges en dehors du plan xy . Pour les deux images, le graphique de gauche indique l’amplitude du déplacement par des échelles de couleurs, tandis que celui de droite indique le déplacement réel des tiges dans l’espace.
Animation du comportement des tiges lorsque l’appareil est en rotation autour de l’axe y, causant des vibrations hors du plan. A gauche, l’amplitude du déplacement est représentée par des échelles de couleurs, tandis que l’animation de droite montre le mouvement dans l’espace.
Vous êtes ici, à la fin (et au commencement…)
Merci d’avoir navigué jusqu’à la fin de cet article ! Votre voyage à travers la modélisation des accéléromètres et des gyroscopes MEMS peut continuer via les liens ci-dessous :
- Foncez au modèle d’accéléromètre : Surface Micromachined Accelerometer
- Faites un tour avec le modèle de gyroscope : Piezoelectric Rate Gyroscope
En savoir plus sur la modélisation des dispositifs piézoélectriques
- Modeling Piezoelectricity: Which Module to Use?
- How to Model Piezoelectric Devices as Both Transmitters and Receivers
- Simulating a MEMS-Based Pressure Sensor Inspired by a Cave Fish
Références
- B. Schweber, “The Autonomous Car: A Diverse Array of Sensors Drives Navigation, Driving, and Performance”, https://www.mouser.com/applications/autonomous-car-sensors-drive-performance/
- D. Purves, G.J. Augustine, D. Fitzpatrick, et al., editors, “The Otolith Organs: The Utricle and Sacculus”, Neuroscience. 2nd edition. Sunderland (MA), Sinauer Associates, 2001; https://www.ncbi.nlm.nih.gov/books/NBK10792/
- T. C. Hain, “Otoliths”, Mar. 2021; https://dizziness-and-balance.com/disorders/bppv/otoliths.html




Commentaires (0)