
Nous avons déjà abordé les paramètres qui permettent de produire un maillage de haute qualité et comment préparer une géométrie de modèle CFD pour le maillage. Dans cet article de blog complémentaire, découvrez le maillage contrôlé par la physique, le raffinement de maillage adaptatif, et comment utiliser une variété d’outils de maillage dans le logiciel COMSOL Multiphysics® pour vos simulations d’écoulements fluides.
Séquences de maillage contrôlées par la physique
Après avoir mis en place les conditions aux limites d’un modèle d’écoulement fluide, COMSOL Multiphysics® permet de faire appel à des séquences de maillage contrôlées par la physique. Ce type de séquence dépend des paramètres suivants:
- Réglages des propriétés des interfaces physiques
- Un modèle de turbulence avec un traitement automatique de la paroi génère par exemple un maillage plus fin qu’un modèle d’écoulement laminaire
- Certaines fonctionnalités
- Les parois peuvent par exemple induire des maillages plus fins et des maillages en couches limites
- Taille de la boîte englobant la géométrie
- Cela contrôle le calibrage de la taille des éléments
La séquence de maillage contrôlée par la physique pour le modèle de corps d’Ahmed, qui est également utilisé dans l’article de blog précédent, ressemble à cela:

Sous le noeud Maillage 1 :
- le sous-noeud Taille contient un ensemble de paramètres de taille de maillage qui dépendent des réglages des propriétés et de la boîte englobante de la géométrie
- le sous-noeud Taille 1 est actif sur l’ensemble des parois non-glissantes et y impose un maillage un peu plus fin
- le sous-noeud Contrôle aux angles vifs 1 identifie tous les angles internes aux parois non-glissantes suffisamment aigus et impose un maillage encore plus fin le long de ces arêtes (dans ce cas, il détecte la plupart des arêtes vives de la voiture, à l’exception d’une reliant le toit et la pente)
- le sous-noeud Tétraèdre libre 1 crée le maillage présent à la fois sur les frontières et dans les domaines
- le sous-noeud Couches limites 1 ajoute un maillage en couches limites sur l’ensemble des frontières non-glissantes
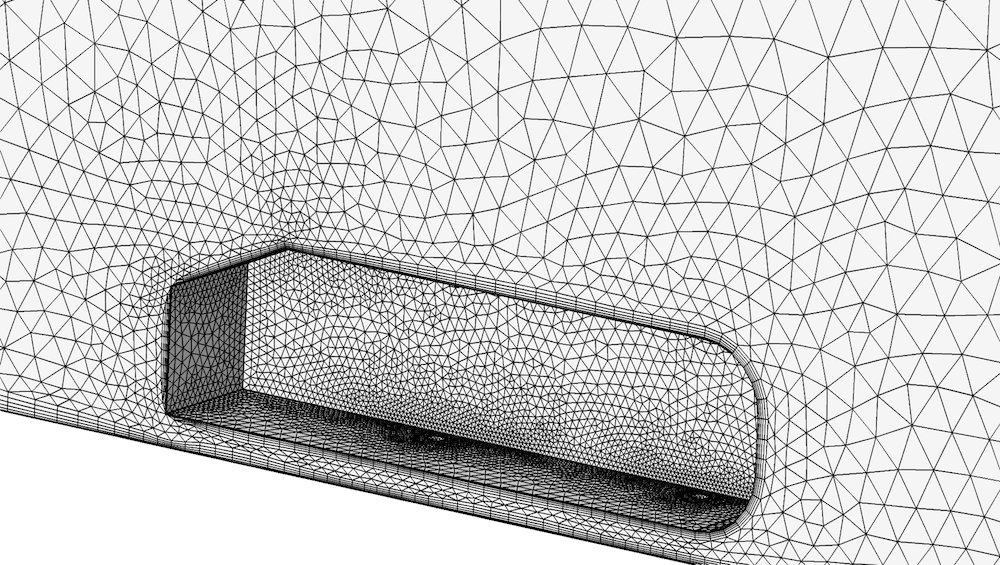
Une vue agrandie du maillage résultant de la séquence de maillage induite par la physique pour le modèle de corps d’Ahmed. On peut observer que le maillage est plus fin sur les parois que dans le volume, et plus fin encore au niveau des arêtes vives. Le maillage en couches limites au contact des parois non-glissantes est également visible.
La séquence induite par la physique peut parfois suffire pour des modèles simples et est toujours un bon point de départ pour des maillages plus avancés. Il est parfaitement possible de résoudre le problème de corps d’Ahmed avec le maillage montré plus haut. Cependant, on peut voir que le domaine de contrôle du maillage dans le sillage de la voiture n’a pas conduit à un maillage plus fin et que le maillage non structuré couvre l’ensemble de la soufflerie. Le maillage pourrait donc être plus fin dans le sillage de la voiture et est inutilement fin loin en aval de la voiture. En utilisant le domaine de contrôle du maillage dans le sillage de la voiture et la surface de partition montrée dans le le premier article de blog de cette série, le nombre total d’éléments pourrait rester constant tout en ayant une bien meilleure résolution dans le sillage.
Outils de maillage pour la modélisation en CFD dans COMSOL Multiphysics®
COMSOL Multiphysics® fournit une large sélection d’outils permettant de contrôler et de générer le maillage. On peut commencer par évoquer les différentes options de maillage de surface, étant donné que l’on recommande de mailler d’abord les surfaces pour vérifier que la résolution est adéquate et que les éléments sont de haute qualité. Notez qu’un outil maillant les entités d’une certaine dimension maille également les entités adjacentes de dimension inférieure adjacentes. Une fonctionnalité Triangle libre, par exemple, maille à la fois les surfaces auxquelles elle est appliquée et l’ensemble des arêtes et points adjacents qui n’étaient pas maillés précédemment. De fait, il n’est pas nécessaire de mailler l’ensemble des arêtes avant de mailler une face, et les volumes peuvent être maillés sans passer par le maillage de l’ensemble des faces englobantes.
Maillage structuré
Un maillage structuré permet de créer les maillages de surface les plus qualitatifs. L’illustration ci-dessous montre un maillage surfacique structuré de haute qualité pour l’un des panneaux du modèle de panneau solaire. Le maillage structuré est raffiné de façon à obtenir des éléments plus fins lorsque l’on s’approche des bords libres et des transitions douces vers les maillages fins couvrant les poutres. L’anisotropie est obtenue en utilisant des noeuds Distribution, qui contiennent des réglages permettant de contrôler le nombre d’éléments et leur distribution le long des arêtes. Le fait que tous les éléments ont des angles à 90° signifie que les éléments ne présentent pas du tout de dissymétrie.
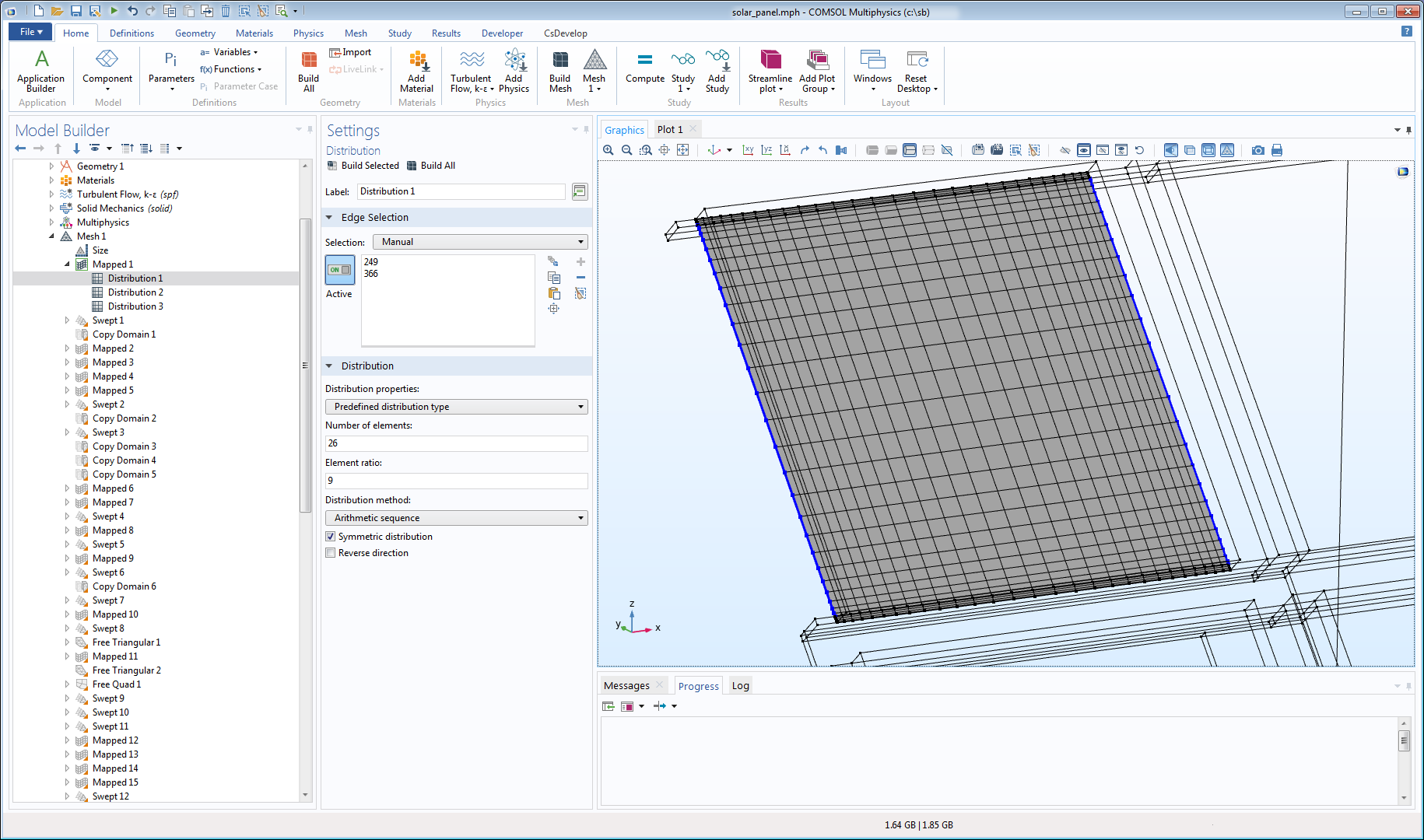
Maillage structuré sur l’une des surfaces du modèle de panneau solaire.
Les maillages surfaciques peuvent être particulièrement puissants pour des simulations 2D telles que le benchmark de profil d’aile NACA 0012 illustré ci-dessous. La propriété la plus intéressante du maillage structuré sur ce modèle est le contrôle extrêmement efficace qu’il propose par rapport à la taille des éléments, leur qualité et leur taux de croissance – même si cela demande un certain effort d’imposer les distributions optimales sur toutes les arêtes.

Un maillage structuré 2D pour le modèle de profil d’aile NACA 0012.
Maillage quadrangulaire non structuré
Certaines surfaces sont tout simplement trop difficiles à diviser en faces qui pourraient être structurées. Dans ce cas, le noeud Quadrangle libre est une option. L’exemple ci-dessous montre la zone dans laquelle la surface d’un des cadres est maillée en quadrangles non structurés. La taille d’élément maximale est contrôlée par un attribut Taille, et des attributs Distribution contrôlent les distributions le long d’un certain nombre d’arêtes.
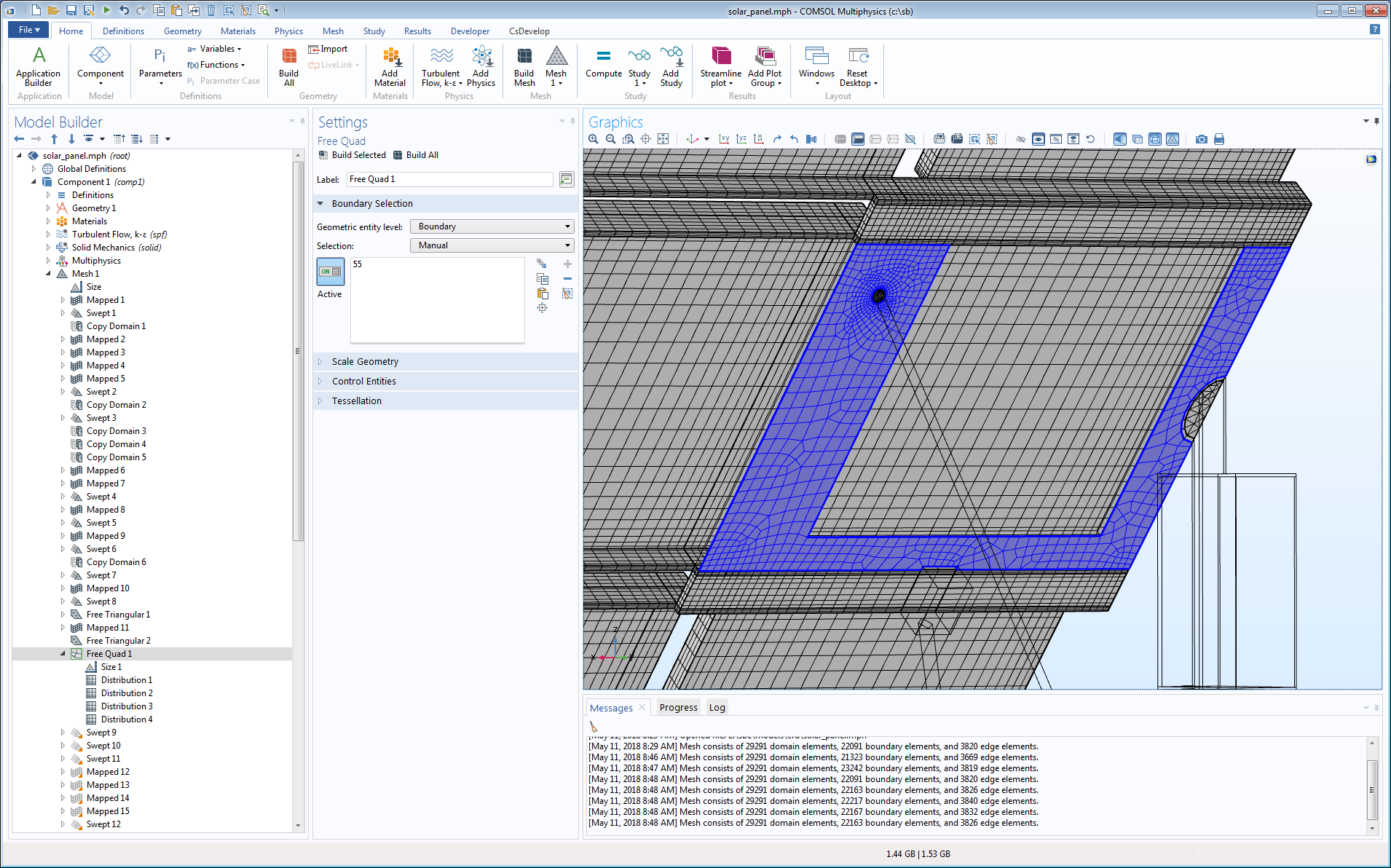
Un maillage en quadrangles non structurés sur une surface du modèle de panneau solaire.
Cette face aurait également pu être maillée avec une opération Triangle libre, mais cela aurait résulté en un plus grand nombre d’éléments. On peut également remarquer que le taux de croissance, mesuré à partir des maillages structurés adjacents, n’est pas le meilleur. Le cadre étant sur la face inférieure du panneau solaire, il ne se produit pas grand-chose du point de vue de l’écoulement. Le maillage influence plutôt la partie mécanique du modèle, pour laquelle le taux de croissance n’est pas un problème.
Maillage triangulaire
L’opération Triangle libre est la “bête de somme” des modèles de CFD 2D, étant donné la simplicité et la rapidité avec laquelle elle permet d’obtenir des maillages de haute qualité sur l’ensemble de la géométrie. La facilité de création des maillages non structurés a toutefois un coût. Les maillages non structurés triangulaires produisent plus de diffusion numérique que les maillages structurés. Cela signifie qu’à taille d’éléments comparable, les solutions obtenues sur des maillages non structurés sont plus diffuses que des solutions obtenues sur un maillage structuré. D’autre part, les maillages non structurés ne peuvent pas présenter de forte anisotropie sans devenir dissymétriques.
De façon générale, les maillages non structurés doivent être plus fins que les maillages structurés pour obtenir le même niveau de précision pour les problèmes CFD. Cependant, la diffusion supplémentaire peut parfois être utile et souhaitée, étant donné qu’elle facilite la convergence. C’est parfait pour un modèle comme l’éjecteur supersonique montré ci-dessous, où le maillage affiché sert de maillage initial pour une adaptation de maillage (voir ci-dessous).
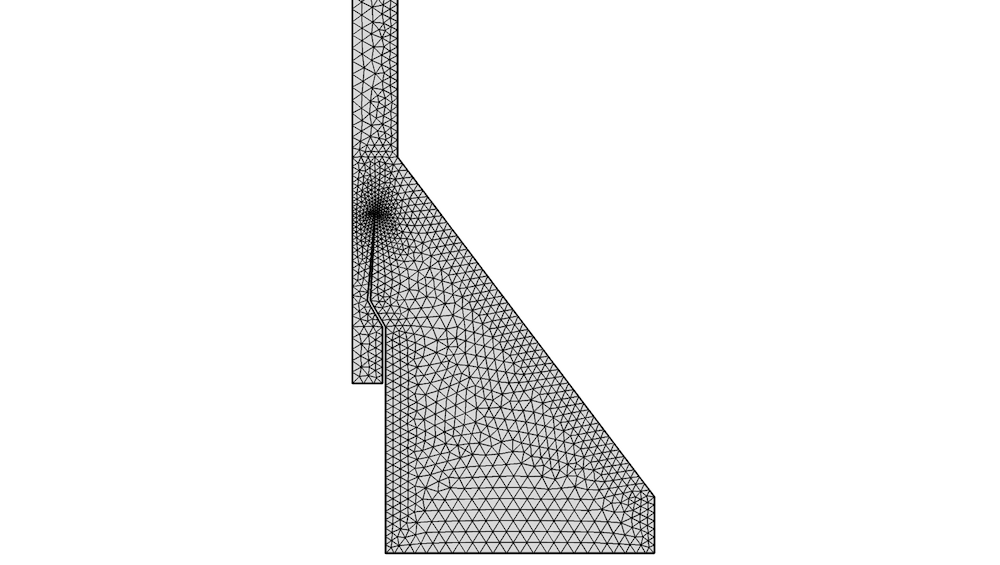
Maillage triangulaire pour un modèle 2D axisymétrique d’éjecteur supersonique.
L’opération Triangle libre a peu d’utilité dans les modèles 3D. L’utilisation principale est de “tester le maillage” de faces individuelles, en particulier les faces sur lesquelles des opérations virtuelles ont été appliquées. On peut analyser la qualité du maillage sur des faces individuelles sans mailler l’ensemble du volume adjacent. Un maillage non structuré triangulaire peut également servir de point de départ pour des maillages extrudés. Ce type de stratégie résulte en un maillage constitué d’éléments prismatiques dont les faces quadratiques peuvent être étirées, créant de fait un maillage anisotrope.
Maillage tétraédrique
La plupart des géométries d’applications industrielles contiennent un ou plusieurs domaines qu’il est difficile de mailler par extrusion. Ces domaines doivent donc être représentés par un maillage tétraédrique. L’opération Tétraèdre libre construit un maillage surfacique sur les surfaces non maillées avant de construire le maillage en volume. Le maillage de surface doit se conformer aux frontières géométriques, mais des noeuds du Maillage surfacique peuvent être déplacés sur les faces au cours de l’optimisation de la qualité des éléments. Cependant, les surfaces déjà maillées sont figées, ce qui peut aboutir à une qualité d’élément plus basse.
Un tétraèdre n’a que des faces triangulaires, il est donc nécessaire que quelque-chose permette de faire la transition avec des éléments dont les faces sont des éléments quadrangulaires. Ce “quelque-chose” est la pyramide. Sur le principe, un élément pyramidal est un hexaèdre dans lequel l’une des faces est réduite à un point, laissant un élément avec une face quadrangulaire et quatre faces triangulaires. Le modèle de panneau solaire contient un grand nombre de faces avec des éléments quadrangles et requiert par conséquent des pyramides pour passer au maillage non structuré dans le domaine autour du panneau solaire, comme montré ci-dessous.
Nous entendons parfois que les pyramides sont inférieures à d’autres types d’éléments, mais il n’y a rien qui rende les pyramides mauvaises en soi. Ceci dit, lorsqu’une pyramide est placée sur un quadrangle anisotrope, sa base doit avoir la même anisotropie. Une petite perturbation de la forme de la pyramide aboutira à un élément ayant une dissymétrie plutôt élevée. C’est ce que l’on peut voir ci-dessous, là où les pyramides placées au-dessus de faces fortement anisotropes au niveau des bords des panneaux ont une qualité typiquement plus faible que les pyramides au centre des panneaux. Dans ce cas, cette qualité inférieure est un prix que l’on paye bien volontiers pour obtenir un maillage globalement plus léger comparé à l’utilisation d’un maillage non structuré dans les panneaux.
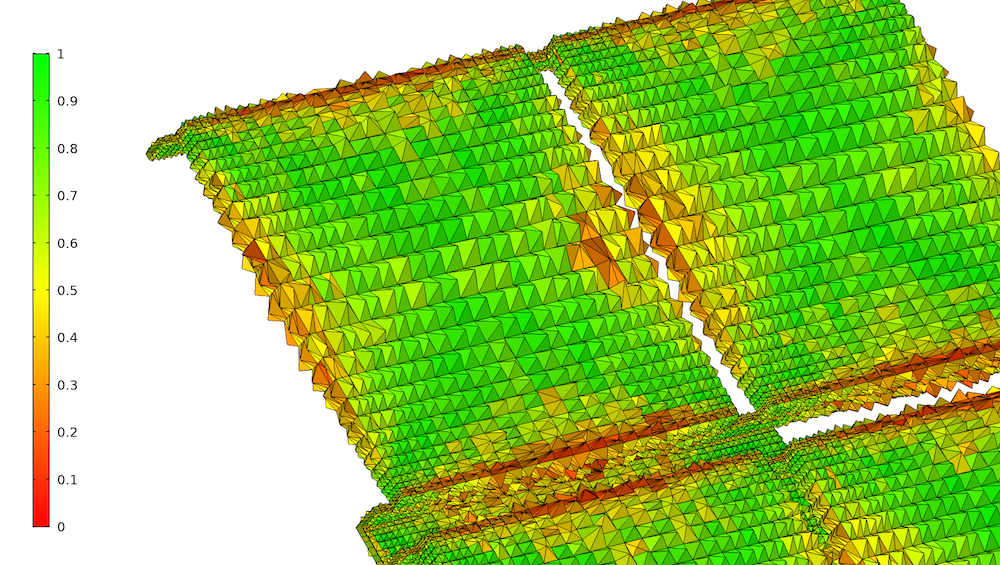
Pyramides placées sur les éléments quadrangulaires de la géométrie du panneau solaire. Les éléments sont colorés en fonction de la qualité calculée à partir de leur dissymétrie.
Le contrôle des maillages générés par l’opération Tétraèdre libre peut être nettement augmenté en utilisant des domaines de contrôle du maillage. Dans l’exemple illustré ci-dessous, l’attribut Taille 3 impose une petite taille d’élément maximale sur la pente et l’arrière du corps d’Ahmed. L’attribut Taille 1 de Tétraèdre libre 1 impose un faible taux de croissance dans le domaine de contrôle du maillage, ce qui produit un maillage fin avec un faible taux de croissance et une qualité d’élément élevée dans le sillage. Lorsque le domaine d’air adjacent est maillé, les frontières englobant le domaine de contrôle du maillage sont retirées, permettant l’ajout du maillage en couches limites et le déplacement des éléments voisins.
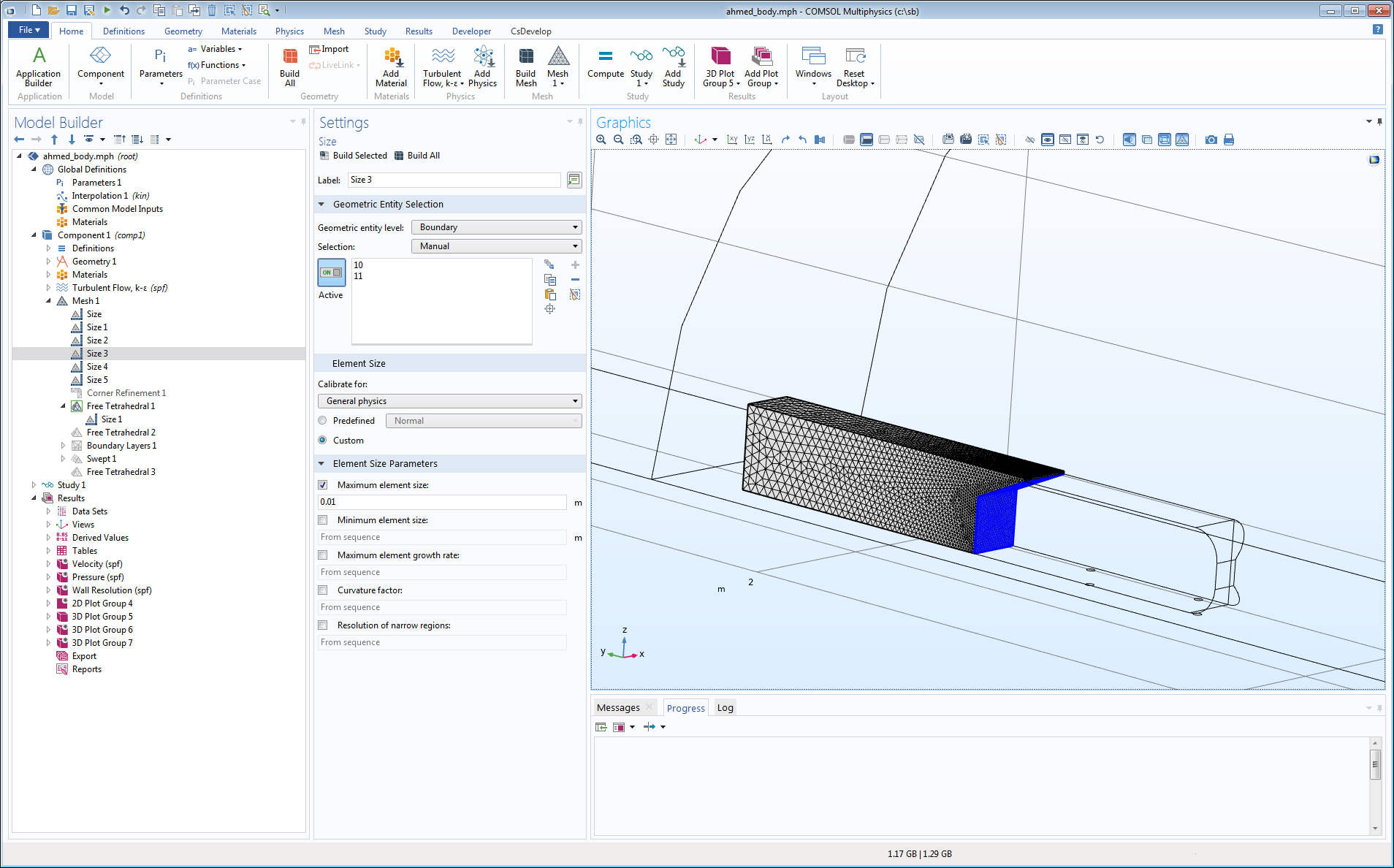
Un domaine de contrôle du maillage dans le sillage du corps d’Ahmed.
Nous aurions pu considérer un maillage extrudé pour le domaine de contrôle de maillage ci-dessus. Cela entraînerait une transition plus difficile vers le reste du maillage non structuré et serait finalement contre-productif, étant donné que les mouvements tourbillonnaires attendus derrière la “voiture” sont relativement isotropes, c’est-à-dire que le maillage structuré devrait lui aussi être plus ou moins isotrope.
Maillage extrudé
L’équivalent 3D du maillage structuré est appelé maillage extrudé dans COMSOL Multiphysics®. L’extrusion prend un ensemble de surfaces sources, les maille, puis les projette sur un certain nombre de surfaces de destination, et connecte ces surfaces à l’aide d’éléments prismatiques ou hexaédriques, selon si la source est maillée avec des éléments triangles ou quadrangles. L’extrusion est la solution idéale pour obtenir des maillages étirés dans la direction de l’écoulement tout en conservant une résolution spécifique dans la section transversale.
Dans l’exemple ci-dessous, un maillage par extrusion est ajouté dans la région de la soufflerie en aval du corps d’Ahmed. Une personne vigilante signalerait que le taux de croissance entre le maillage tétraédrique non structuré et le maillage extrudé proche du plafond pourrait être meilleur. Mais l’écoulement ne montre quasiment pas de variations dans cette zone, il est donc plus important d’obtenir un bon taux de croissance dans le sillage en aval de la “voiture”.
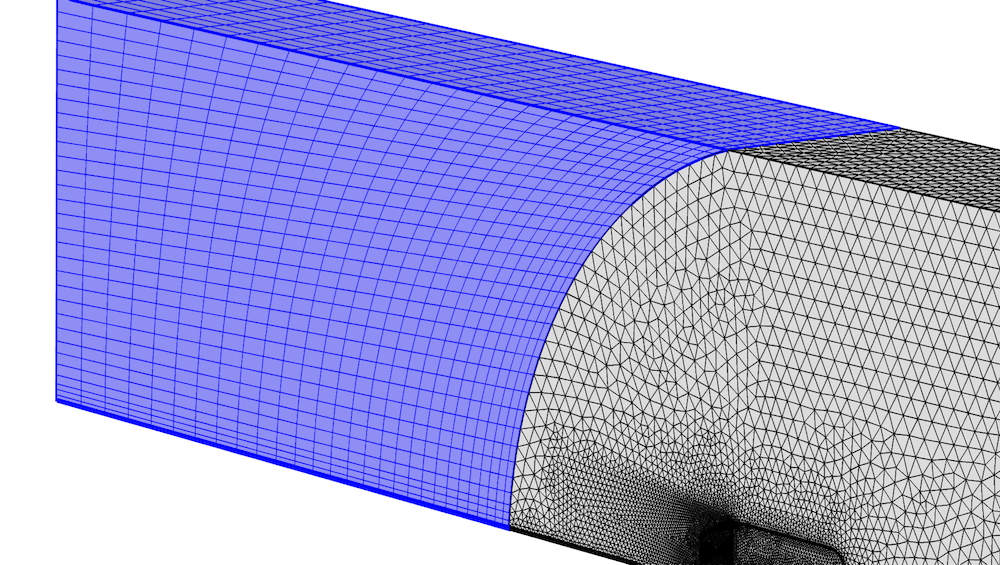
Maillage extrudé en aval du corps d’Ahmed.
Le maillage extrudé ci-dessus utilise le maillage surfacique résultant d’une opération Tétraèdre libre et d’une opération Couches limites comme maillage source. C’est une stratégie souvent utile. On aurait pu créer un maillage triangulaire non structuré sur la frontière de sortie et l’extruder de la sortie jusqu’à la surface incurvée. Cela aurait cependant, ajouté des restrictions sur l’opération Tétraèdre libre (voir la section “Maillage triangulaire”). On aurait également eu besoin d’insérer les éléments de couche limite le long de l’ensemble du sol de la soufflerie, tandis qu’ici le maillage en couches limites a été créé uniquement dans la partie contenant le maillage non structuré puis extrudé en aval.
Maillage en couches limites
Le maillage en couches limites, primordial pour des simulations CFD, crée des maillages fortement anisotropes aux abords des parois sans avoir à faire appel à un maillage extrudé ou des domaines spécifiquement créés. Ces éléments sont nécessaires à cause des couches limites qui se forment généralement au niveau des parois non-glissantes, décrites dans cet article de blog précédent.
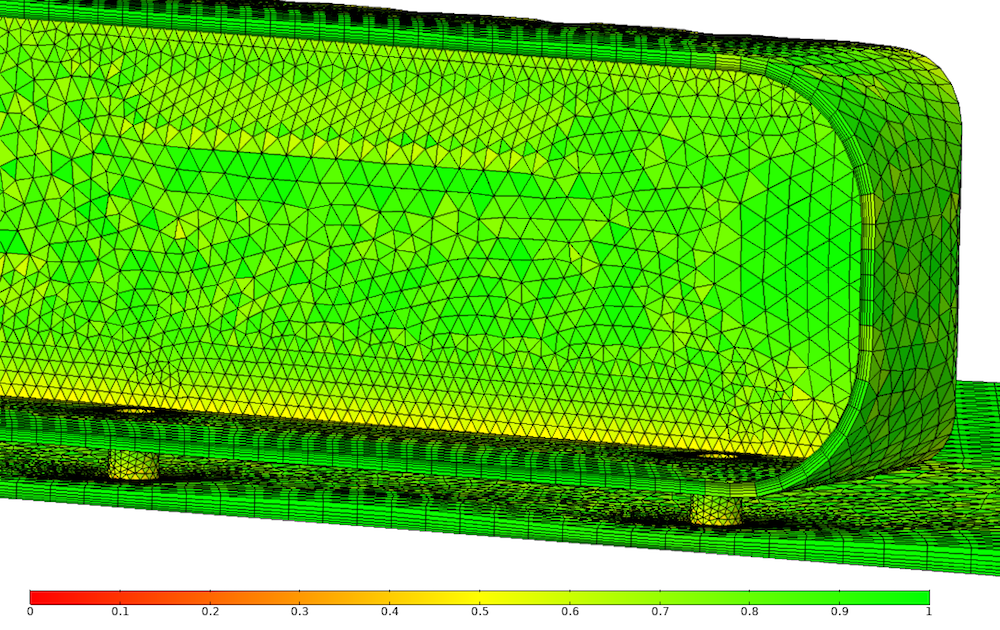
Maillage en couches limites pour le modèle de corps d’Ahmed. La couleur des éléments est liée à leur qualité, basée sur la dissymétrie.
Dans COMSOL Multiphysics®, les maillages en couches limites sont ajoutés une fois que le domaine a été maillé. Des éléments anisotropes prismatiques ou hexaédriques sont introduits et poussés dans le domaine de calcul, conduisant à un certain nombre d’éléments fortement anisotropes comme vous pouvez le voir ci-dessous. Observez la qualité du maillage, bonne malgré l’anisotropie. Ceci est dû au fait que le maillage en couches limites est créé ici à partir de triangles de bonne qualité, conduisant à des éléments prismatiques eux aussi de bonne qualité.
Caractéristiques du maillage en couches limites
Le maillage en couches limites a trois caractéristiques:
- Hauteur de la première couche
- Taux de croissance
- Nombre de couches
La première est la hauteur du premier élément et est souvent définie comme une fraction de l’échelle de longueur de l’élément surfacique. Un paramétrage par défaut typique est une échelle de longueur d’élément surfacique 50 fois plus grande que la hauteur du premier élément de la couches limites. Des rapports d’aspects plus élevés permettent d’obtenir une meilleure résolution, mais le système d’équations résultant peut aussi être plus difficile à résoudre, d’autant plus en utilisant des solveurs itératifs.
La deuxième caractéristique est le facteur d’étirement, c’est-à-dire le taux de croissance d’une couche d’éléments à l’autre. Il est nécessaire pour obtenir une bonne transition vers le maillage non structuré (comme illustré plus haut). Le saut de taille des éléments lors de la transition de la couche limite vers le maillage non structuré est clairement visible. La couche limite pourrait bénéficier d’un facteur d’étirement plus élevé ou d’un plus grand nombre de couches dans le maillage de la couche limite (le nombre de couches est la troisième caractéristique du maillage en couches limites). Mais le maillage en couches limites montré plus haut ne peut pas être bien plus épais, étant donné que le maillage de l’espace entre la voiture et le sol est déjà relativement écrasé pour éviter une dissymétrie importante du maillage non structuré. Cette compression du maillage en couches limites est faite automatiquement par l’algorithme sous-jacent.
Choisir l’épaisseur de la première couche, le taux de croissance et le nombre de couches est un exercice d’équilibre entre la résolution nécessaire, une bonne transition vers le maillage non structuré, et la qualité des éléments obtenus.
Considérations particulières pour les arêtes vives
Si vous avez déjà emballé vos propres cadeaux, vous savez avec quelle facilité le papier peut se déchirer lorsqu’il est tendu autour d’arêtes vives. Les maillages en couches limites ont des problèmes similaires, comme vous pouvez le voir ci-dessous. Les éléments du maillage en couches limites au niveau de l’angle vif du bord de fuite présentent une certaine dissymétrie, tout comme les éléments en aval du profil d’aile.
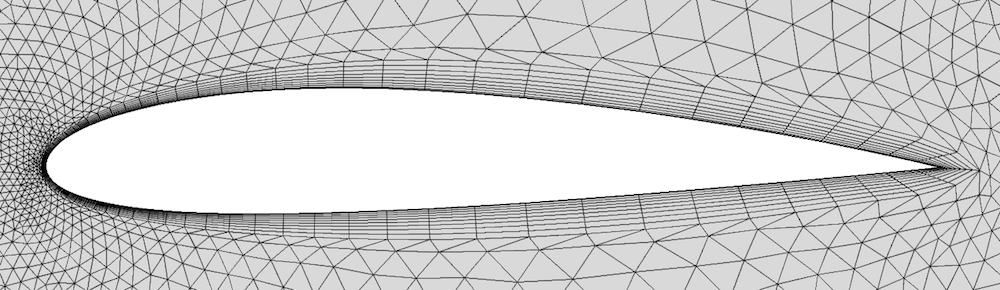
L’arête vive constituant le bord de fuite d’un profil d’aile sans manipulation spéciale du maillage.
Une option consiste à “diviser” la couche limite au niveau des arêtes vives. Le résultat est visible dans l’image centrale ci-dessous. La couche limite se termine désormais avec deux colonnes spéciales d’éléments, chacune démarrant avec un triangle suivi du nombre adéquat d’éléments quadrangles. Diviser vous permet de contrôler à quel point un angle doit être vif pour être considéré comme tel, ainsi que l’angle maximal que chaque colonne “spéciale” d’élément doit couvrir. Optimiser ces paramètres permet d’améliorer considérablement la qualité des éléments au niveau d’arêtes vives.
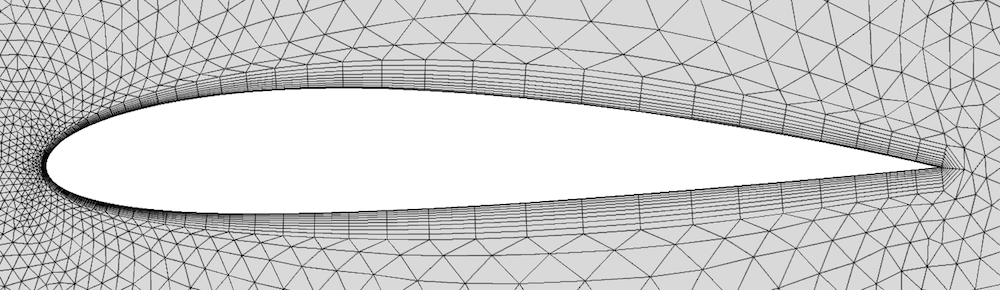
Division de la couche limite au niveau du bord de fuite d’un profil d’aile.
L’option Division ne fonctionne pas toujours. Des géométries CAO 3D complexes, dans lesquelles un certain nombre d’arêtes peuvent être connectées à un angle vif, sont particulièrement difficiles à traiter. L’algorithme doit être programmé pour chaque configuration topologique unique, et il est fort possible qu’une géométrie avancée contienne au moins un angle vif que l’algorithme ne saura pas traiter.
Le troisième traitement d’angles vifs peut alors être une option. Il s’appelle rognage et est l’option utilisée par défaut pour les angles vifs dans COMSOL Multiphysics®. Le résultat pour le profil d’aile est montré ci-dessous. Au fur et à mesure que la couche s’approche de l’arête vive, sa hauteur diminue de deux éléments pour chaque élément qui se rapproche de l’arête. La méthode peut également être vue comme une croissance du nombre d’éléments de couches limites depuis l’arête vive. Le nombre d’éléments pour le décrément de couche et l’angle minimum de rognage peuvent tous deux être contrôlés afin d’optimiser le maillage.
Le rognage réduit la résolution effective au niveau de l’angle vif, par rapport à l’absence de manipulation spéciale du maillage ou à la division. Le rognage devrait donc toujours être combiné à un raffinement général du maillage, c’est pourquoi la fonctionnalité Contrôle aux angles vifs discutée plus haut est incluse par défaut dans les séquences de maillage induites par la physique.
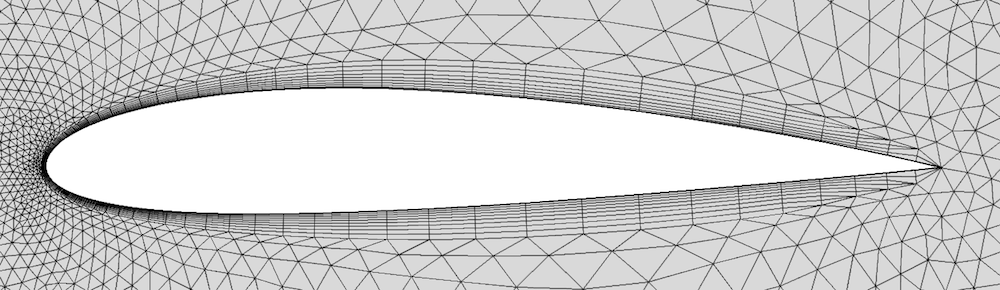
Rognage, l’option par défaut pour le maillage d’une couche limite avec des angles vifs.
Les maillages en couches limites peuvent augmenter la résolution des régions minces. Si vous observez attentivement le maillage dans l’image plus haut, la zone entre la voiture et le sol est couverte par 15 éléments (6 + 3 + 6). C’est suffisant pour représenter n’importe quel profil de vitesse se produisant dans cette région mince. Sans la couche limite, l’espace serait couvert de 3 éléments seulement, ce qui limiterait considérablement la capacité du maillage à représenter le profil d’écoulement sous le corps d’Ahmed. L’écoulement serait de fait artificiellement étranglé et la région mince apparaîtrait numériquement plus mince qu’elle ne l’est géométriquement. Les maillages en couches limites peuvent donc être utiles, pas seulement pour les couches limites turbulentes, mais aussi dans des systèmes laminaires voire même microfluidiques. Une bonne pratique: les régions minces doivent être résolues avec au moins cinq éléments dans leur épaisseur.
Copie de maillages
Nous allons enfin parler de la copie du maillage d’une entité à une autre. C’est possible pour des entités de même dimension tant que le maillage de la source peut être projeté sur l’entité de destination par une translation, une rotation et une mise à l’échelle isotrope. Cela signifie que la destination doit avoir la même forme que la source, mais elle peut être située à un autre endroit, tournée d’une certaine façon et avoir une taille différente.
La copie de maillage est particulièrement intéressante dans le cas de maillages structurés et extrudés. Copier nous permet de remplacer un certain nombre d’opérations de création de maillage structuré et d’extrusions et un certain nombre d’attributs de distribution par une seule opération de copie. C’est possible si la géométrie a été partitionnée correctement, comme cela a été discuté dans l’article de blog précédent. En plus d’économiser du travail dans la création du maillage, n’importe quelle modification du maillage est plus simple à mettre en place, puisque vous n’avez besoin de modifier que la séquence du domaine source. L’opération de copie transfère automatiquement ces changements vers les domaines de destination.
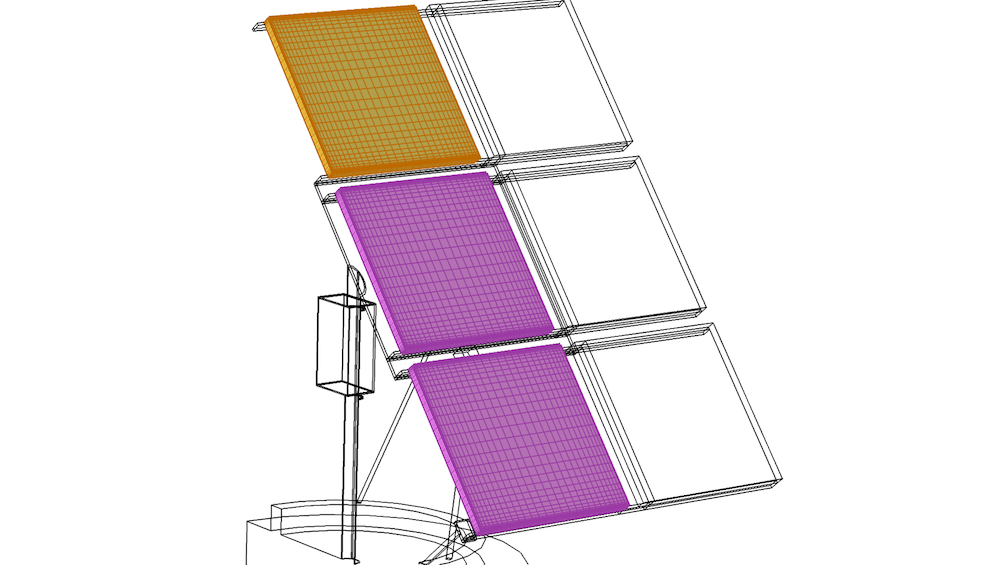
Le maillage extrudé du domaine en jaune est copié vers les deux domaines en rose.
Maillage adaptatif
Lorsque l’on simule des problèmes de CFD, on s’efforce de créer des maillages denses dans les régions où les gradients sont importants. Dans certains cas, néanmoins, prédire dans quelles zones les gradients importants apparaîtront peut s’avérer difficile. Il y a aussi des cas transitoires dans lesquels les forts gradients se déplacent. On pourrait adresser ce type de problème en maillant finement l’ensemble des régions dans lesquelles les forts gradients apparaissent, mais cela est coûteux en termes de ressources. A la place, une solution est de faire appel à un maillage adaptatif.
Maillage adaptatif pour les calculs stationnaires
Les profils de pression de chocs créés par un écoulement transsonique au-dessus d’une bosse située sur une paroi constituent un bon exemple pour utiliser un maillage adaptatif. Les chocs peuvent être capturés par le schéma de stabilisation, mais des maillages grossiers les rendraient plus diffus.

Isobares d’un écoulement d’Euler au-dessus d’une bosse située sur une paroi.
Les chocs nets sur l’image ci-dessus sont obtenus en commençant avec un maillage homogène et relativement grossier (visible ci-dessous à gauche). La solution sur le maillage grossier est utilisée pour calculer l’approximation du résidu de l’équation et raffiner le maillage dans les zones où le résidu est grand. Les équations sont ensuite résolues sur le maillage raffiné résultant. Cette procédure peut être répétée jusqu’à l’obtention de la précision satisfaisante.
Le maillage utilisé pour calculer le champ de pression de l’illustration plus haut est montré ci-dessous à droite. Il résulte d’un premier maillage très simple ayant été raffiné deux fois par adaptation. L’adaptation nécessite tout de même un certain travail de création du maillage initial, puisque le problème doit converger sur ce maillage.
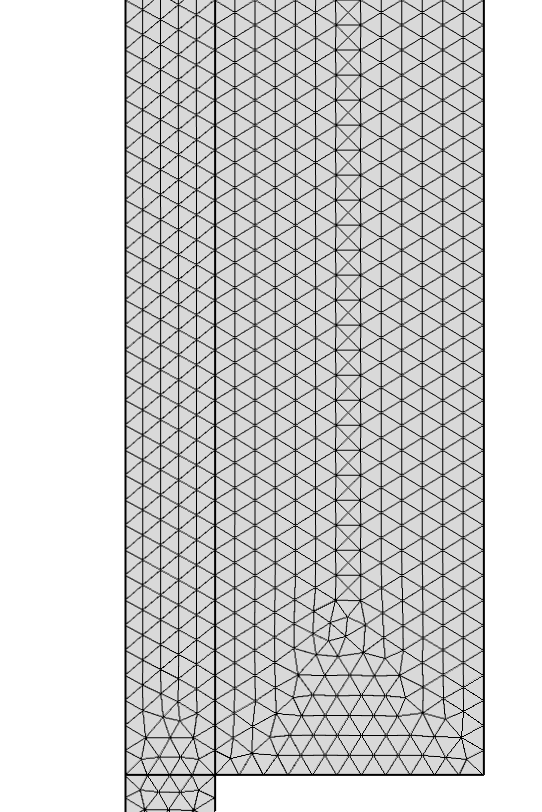
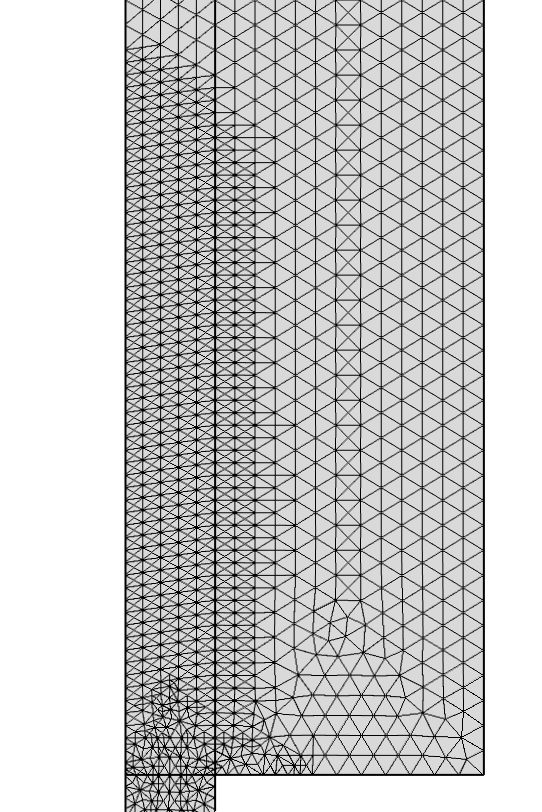
Maillage initial (gauche) et maillage adapté (droite) pour le modèle d’écoulement d’Euler.
Maillage adaptatif pour des problèmes transitoires
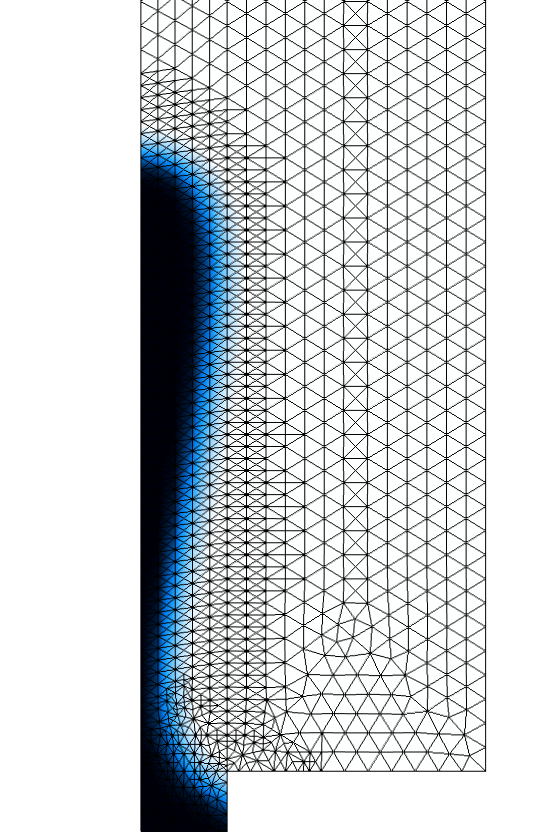
Pour des modèles transitoires, l’adaptation fonctionne un peu différemment. Un maillage de base grossier est utilisé pour faire avancer la solution pendant un certain intervalle de temps. La solution est ensuite utilisée à nouveau pour raffiner le maillage en se basant sur une fonction servant d’indicateur. Le maillage adapté est utilisé pour simuler à nouveau l’intervalle de temps. L’image ci-dessous à gauche montre le maillage de base d’un modèle de buse de jet d’encre, et l’image centrale montre le maillage adapté. Etant donné qu’il s’agit d’un modèle diphasique, l’adaptation est basée sur \|\nabla \phi\|, où \phi est la fonction Level Set (0 dans une phase et 1 dans l’autre). L’image de droite montre la solution à la fin d’un intervalle de temps d’adaptation. On peut voir comment le maillage raffiné représente le transport de l’interface pendant tout l’intervalle de temps.
Adaptation de maillage temporelle sur un modèle de buse jet d’encre.
Le maillage adaptatif en temps constitue une méthode qui peut être économe tout en permettant d’obtenir d’excellents résultats. Son efficacité est fortement liée au maillage de base, qui ne peut pas être trop fin, étant donné que le problème doit être résolu sur un instant supplémentaire sur ce maillage de base. Travailler le maillage de base est souvent bénéfique, particulièrement dans le cas de géométries plus avancées.
Conclusions sur les outils de maillage pour les problèmes CFD
Créer un bon maillage pour des problèmes CFD est tout un art. Même en utilisant le maillage adaptatif, un maillage de haute qualité est le fruit d’une bonne compréhension du fonctionnement des divers outils de maillage mais aussi de l’anticipation de la solution attendue pour l’écoulement.
Le premier maillage que l’on crée est rarement suffisant, et il est souvent nécessaire de retravailler la géométrie, le maillage, ou les deux. Pour cette raison, les séquences de géométrie et de maillage dans COMSOL Multiphysics® sont très utiles. Une modification introduite dans la séquence de géométrie est répercutée dans l’ensemble du modèle, il n’est donc pas nécessaire de préciser à nouveau comment les différentes interfaces physiques s’appliquent ou de modifier le paramétrage du maillage lorsque la géométrie est modifiée. On peut aussi modifier le paramétrage du maillage de façon importante et reconstruire l’ensemble de la séquence de maillage sans tout recommencer de zéro. Une alternative est d’utiliser des paramètres à la fois pour la géométrie et le maillage de façon à obtenir un modèle dans lequel le maillage peut être raffiné en quelques clics.
Cette série d’articles de blog a à peine effleuré les capacités de création de maillage de COMSOL Multiphysics®. Il existe de nombreux réglages et options qui n’ont pas été mentionnés ici et dont les modèles de CFD pourraient largement bénéficier.
Prochaines étapes
Pour aller plus loin
Pour en savoir plus sur le maillage et les analyses CFD, consultez le blog COMSOL:





Commentaires (0)