Utiliser les couches parfaitement adaptées et les conditions de diffusion à la frontière pour les problèmes d’électromagnétisme ondulatoire

Lors de la résolution de problèmes d’électromagnétisme ondulatoires, on peut être amené à modéliser un domaine ayant des frontières ouvertes, c’est-à-dire des frontières du domaine de calcul à travers lesquelles une onde électromagnétique peut passer sans être réfléchie. COMSOL Multiphysics^® propose plusieurs solutions pour cela. Dans ce blog, nous allons examiner l’utilisation des conditions de diffusion à la frontière et des couches parfaitement adaptées pour tronquer des domaines et analyser leurs avantages respectifs.

Pourquoi tronquer les domaines ?

Nous sommes souvent intéressés par la modélisation d’un objet rayonnant, tel qu’une antenne dans un espace libre. Nous pouvons construire un tel modèle dans le but de simuler une antenne sur un satellite dans l’espace lointain ou, plus souvent, une antenne montée dans une chambre d’essai anéchoïque.

Une antenne dans un espace libre infini. Nous souhaitons seulement modéliser une petite région autour de l’antenne.

Ce type de modèles peut être réalisé à l’aide de la formulation Ondes électromagnétiques, domaine fréquentiel du module RF ou du module Wave Optics. Ces modules fournissent des interfaces similaires pour résoudre la forme fréquentielle des équations de Maxwell via la méthode des éléments finis. (Pour une description des principales différences entre ces modules, veuillez consulter mon précédent blog, intitulé “Quel module utiliser pour les simulations d’électromagnétisme ?“)

Dans ce blog, nous nous limiterons à des problèmes en 2D, où l’onde électromagnétique se propage dans le plan xy, avec le champ électrique polarisé dans la direction z. Nous supposerons en outre que notre domaine de modélisation correspond à du vide absolu, la forme des équations de Maxwell étant ainsi réduite à:

où E_z est le champ électrique, la perméabilité et la permittivité du vide \mu_r = \epsilon_r = 1 , et k_0 étant le nombre d’onde.

La résolution de l’équation ci-dessus par la méthode des éléments finis nécessite un domaine de modélisation de taille finie, ainsi qu’un ensemble de conditions aux limites. Au niveau des frontières extérieures, nous voulons utiliser des conditions aux limites transparentes à tout rayonnement. Ainsi, notre domaine tronqué sera une approximation raisonnable de l’espace vide. Nous souhaitons également que ce domaine tronqué soit aussi petit que possible, car réduire la taille de notre modèle permet de diminuer les coûts de calcul.

Examinons maintenant deux des fonctionnalités disponibles dans l’environnement de simulation COMSOL Multiphysics^® pour tronquer votre domaine de modélisation: la condition de diffusion à la frontière et la couche parfaitement adaptée.

La condition de diffusion à la frontière

L’une des premières conditions aux limites de transparence formulées pour les problèmes ondulatoires a été la condition de rayonnement de Sommerfeld, qui, pour des champs 2D, peut être écrite ainsi:

où r est la coordonnée radiale.

Cette condition est exactement non-réfléchissante lorsque les frontières de notre domaine de modélisation sont infiniment éloignées de notre source, mais on ne peut évidemment pas utiliser un domaine de modélisation infiniment grand. Ainsi, bien que nous ne puissions pas appliquer de façon exacte la condition de Sommerfeld, nous pouvons appliquer une approximation raisonnable de celle-ci.

Considérons maintenant la condition limite:

Vous pouvez clairement voir les similitudes entre cette condition et la condition de Sommerfeld. Cette condition limite est appelée de manière plus formelle une condition de diffusion à la frontière du premier ordre (SBC: scattering boundary condition) et sa mise en oeuvre dans COMSOL Multiphysics^® est triviale. En fait, ce n’est rien d’autre qu’une condition limite de Robin avec un coefficient à valeur complexe.

Si vous souhaitez voir un exemple d’équation d’onde 2D implémentée à partir de zéro avec cette condition limite, vous pouvez consulter le modèle d’application de diagrammes de diffraction.

Cette condition est toutefois soumise à une limitation importante. Elle est non-réfléchissante seulement si le rayonnement incident est parfaitement normal par rapport à la frontière. Toute onde incidente sur la SBC ayant une incidence éloignée de la normale sera partiellement réfléchie. Le coefficient de réflexion d’une onde plane incidente sur une SBC du premier ordre pour une incidence variable est tracé ci-dessous.

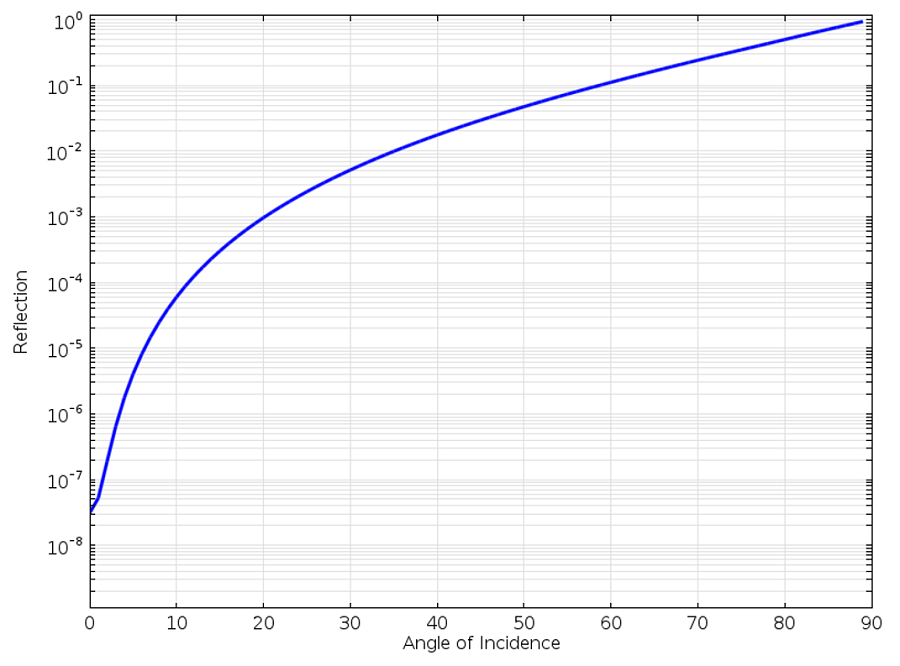
Réflexion d’une onde plane au niveau d’une SBC du premier ordre en fonction de l’angle d’incidence.

Nous pouvons observer sur le graphique ci-dessus que lorsque l’onde plane entrante arrive avec une incidence rasante, l’onde est presque entièrement réfléchie. A un angle d’incidence de 60°, la réflexion est d’environ 10 %, nous indiquant clairement la nécessité d’utiliser une meilleure condition limite.

COMSOL Multiphysics^® inclut également (comme pour la version 4.4) la SBC du second ordre:

Cette équation ajoute un second terme, qui utilise la dérivée seconde tangentielle du champ électrique le long de la frontière. Cette équation est également plutôt simple à mettre en œuvre dans l’architecture logicielle de COMSOL^®.

Comparons les coefficients de réflexion de la SBC du premier ordre et de la SBC du second ordre:

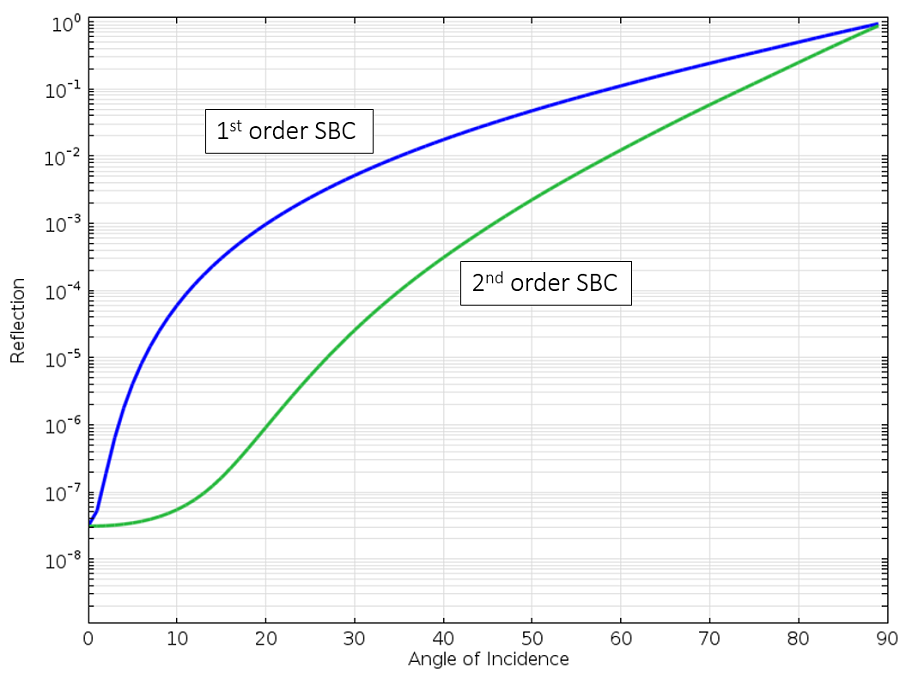
Réflexion d’une onde plane au niveau des SBC de premier et de second ordre en fonction de l’angle d’incidence.

Nous pouvons voir que la SBC de second ordre est uniformément meilleure. Nous pouvons maintenant atteindre un angle d’incidence de ~75° avant que la réflexion n’atteigne 10%. C’est mieux, mais ce n’est pas encore le meilleur résultat que nous sommes capables d’obtenir. Eloignons nous maintenant de ce type de conditions limites et examinons les PML.

La PML – couche parfaitement adaptée

Pour rappel, notre objectif est de simuler une situation typique d’une antenne dans une chambre anéchoïque, une pièce dont les murs sont recouverts de pointes pyramidales en matériau absorbant, réduisant au minimum toute réflexion du signal. On peut considérer ceci comme notre analogie physique avec la couche parfaitement adaptée (PML: perfectly matched layer), qui n’est pas une condition limite, mais plutôt un domaine que nous ajoutons sur l’extérieur du modèle et qui devrait absorber toutes les ondes sortantes.

D’un point de vue mathématique, la PML est simplement un domaine dont la permittivité et la perméabilité sont anisotropes et à valeurs complexes. Pour un aperçu d’utilisation de ces tenseurs, voir Theory and Computation of Electromagnetic Fields. Bien que les PML soient théoriquement non réfléchissantes, elles présentent de la réflexion induite par la discrétisation numérique: le maillage. Pour minimiser cette réflexion, nous devons utiliser un maillage dans la PML qui s’aligne sur l’anisotropie des propriétés du matériau. Les maillages de PML adéquats sont indiqués ci-dessous, pour les domaines 2D circulaires et 3D sphériques. Les PML cartésiennes et sphériques et leurs utilisations appropriées sont également abordées dans la documentation produit.

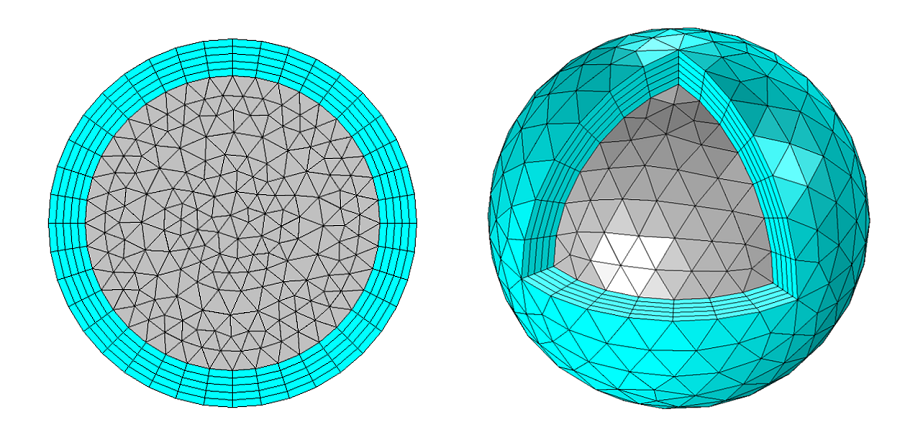
Maillages adéquats pour des PMLs sphériques 2D et 3D.

Dans COMSOL Multiphysics^® 5.0, ces maillages peuvent être automatiquement mis en place pour les problèmes 3D à l’aide du maillage contrôlé par la physique, comme montré dans cette vidéo.

Examinons maintenant la réflexion sur une PML en fonction de l’angle d’incidence par rapport aux SBC:

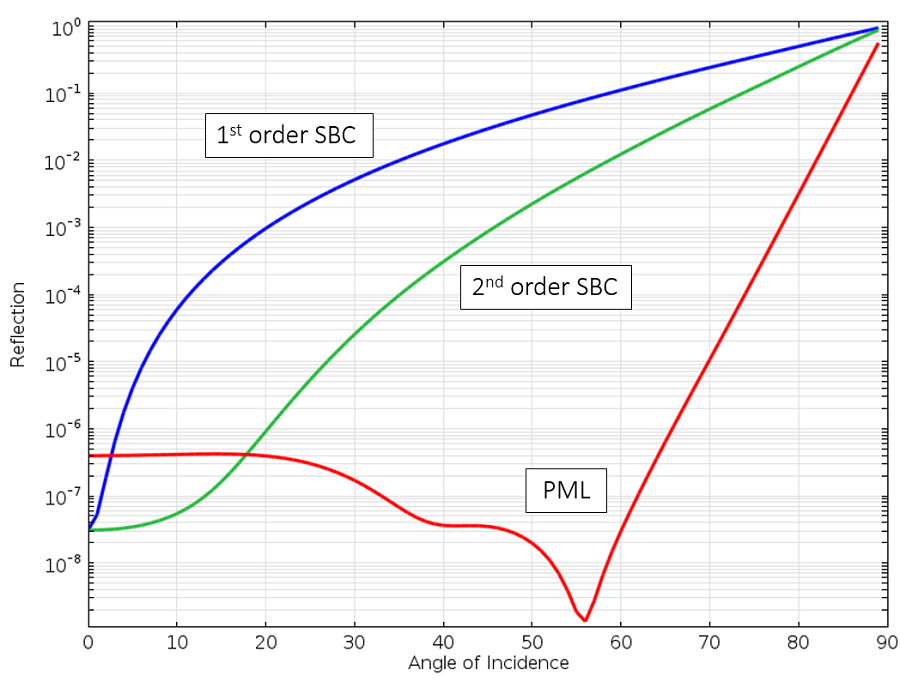
Réflexion d’une onde plane au niveau des SBC de premier et second ordre et de la PML en fonction de l’angle d’incidence.

Nous pouvons constater que la PML est la moins réfléchissante sur la plage la plus large. Il y a encore des réflexions lorsque l’onde se propage de façon quasi parallèle à la frontière, mais heureusement on rencontre assez rarement de tels cas en pratique. Une autre caractéristique de la PML, que nous ne détaillerons pas pour l’instant, est qu’elle absorbe non seulement l’onde qui se propage, mais également tout champ évanescent. D’un point de vue physique, la PML peut donc être considérée comme un matériau presque parfaitement absorbant.

Quelle option devrait-on alors choisir ?

Il est clair que la PML est la meilleure des approches décrites ici. Cependant, la PML utilise plus de mémoire que la SBC.

Par conséquent, si vous en êtes au début de la modélisation et que vous souhaitez construire un modèle un peu moins gourmand en ressources, la SBC du second ordre est une bonne option. Vous pouvez également l’utiliser dans des situations où vous avez de bonnes raisons de croire que toute réflexion au niveau de la SBC n’affectera pas beaucoup les résultats qui vous intéressent.

La SBC du premier ordre est actuellement l’option par défaut, pour des raisons de compatibilité avec les versions précédentes du logiciel, mais avec COMSOL Multiphysics^® version 4.4 ou supérieure, utilisez la SBC du second ordre. Nous n’avons présenté ici que la forme d’onde plane de la SBC, mais les formes d’onde cylindrique et d’onde sphérique (en 3D) des SBC de premier et de second ordre sont également disponibles. Bien qu’elles utilisent moins de mémoire, elles génèrent toutes plus de réflexion que les PML.

Les SBC et les PML sont des conditions appropriées pour représenter des frontières ouvertes sur lesquelles on ne connaît pas bien les champs situés à ces frontières. En revanche, si vous souhaitez modéliser une frontière ouverte où les champs sont connus pour avoir une certaine forme, telle qu’une frontière représentant un guide d’ondes, les conditions aux limites de port et de port réduit sont plus appropriées. Nous aborderons ces conditions dans un prochain blog.