
Comprendre les différentes options d’excitation électromagnétique transitoire
Lorsqu’on modélise des signaux électriques qui varient arbitrairement dans le temps, on peut généralement utiliser l’interface Courants électriques du logiciel COMSOL Multiphysics® pour calculer la réponse du système par le biais d’une étude temporelle. Bien qu’il existe plusieurs options d’excitation différentes, il convient généralement de raisonner en termes de signal de courant appliqué ou de signal de tension se propageant le long d’une ligne de transmission. Voyons plus en détail pourquoi.
Table des matières
- Introduction
- Excitation en courant
- Excitations en tension des courants électriques
- Ligne de transmission, Port réduit et Terminal de type terminé
- Connexions des circuits électriques
- Conclusion
Introduction
Nous examinerons ici l’exemple utilisé dans notre précédent article de blog, “Using Different Physics Interfaces for RF Electromagnetic Heating Models”: excitations en domaine fréquentiel d’un câble coaxial inséré dans une cavité métallique remplie d’un échantillon de matériau à pertes diélectriques. Nous utiliserons le même système et appliquerons différents types de signaux transitoires au câble coaxial. Nous comparerons également l’interface physique Courants électriques avec l’interface physique Ondes électromagnétiques, transitoire en termes notamment de calcul de la dissipation totale au sein du matériau. Cette comparaison se justifie par le fait que l’interface Ondes électromagnétiques, transitoire résout la forme vectorielle complète des équations de Maxwell, alors que l’interface Courants électriques résout une approximation simplifiée des équations de Maxwell en ignorant les champs magnétiques et en résolvant uniquement le potentiel électrique scalaire. Pour réduire le coût de calcul de ces exemples,le modèle sera simplifié par une représentation 2D axisymétrique, comme le montre le schéma ci-dessous.
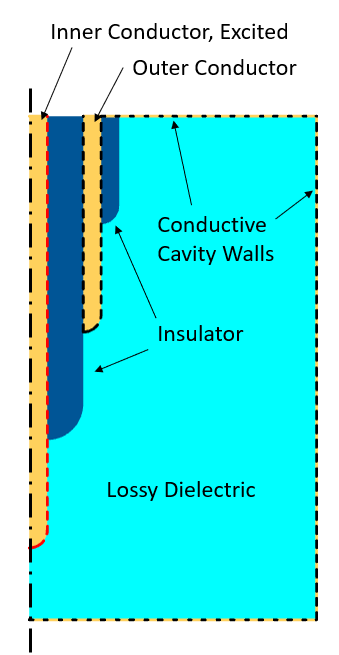
Schéma du modèle dans le plan de modélisation 2D axisymétrique.
Excitation en courant
Nous commençons par exciter le système au moyen d’un courant imposé, variant dans le temps, comme le montre la figure ci-dessous. Le signal est initialement nul, puis augmente progressivement jusqu’à une valeur maximale, ensuite maintenue. Il est possible d’appliquer un lissage à cette fonction en escalier, ce qui sera examiné plus loin. Le système démarre au repos : les champs sont initialement nuls partout. Compte tenu de cette condition initiale et du signal d’entrée, la réponse transitoire du système devrait s’approcher d’une solution stationnaire non nulle après un temps suffisant, ce qui équivaut à une excitation en courant continu du système.
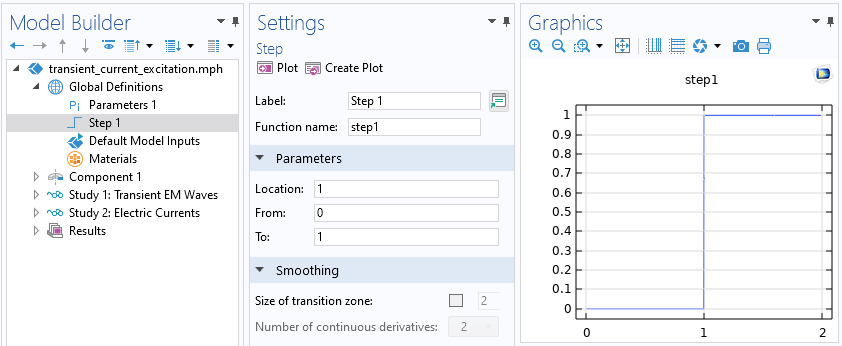
Le signal appliqué est modulé par une fonction Step qui passe de zéro à un, au temps adimensionnel de un. Notez l’option permettant d’inclure le lissage, en l’occurence désactivée.
Nous commencerons par construire un modèle à l’aide de l’interface Ondes électromagnétiques, transitoire car cette interface tient compte de tous les phénomènes résistifs, capacitifs et inductifs. Cette interface est différente de l’interface Ondes électromagnétiques, domaine fréquentiel utilisée précédemment, car elle n’inclut pas de Condition d’impédance de frontière, cette condition limite n’ayant de sens que dans le domaine fréquentiel. Bien qu’il soit possible de modéliser explicitement les fils métalliques, nous allons plutôt modéliser toutes les parties métalliques comme des conducteurs idéaux sans pertes via la condition limite Conducteur électrique parfait. En effet, il a été démontré précédemment que les pertes dans le métal sont relativement négligeables dans ce cas.
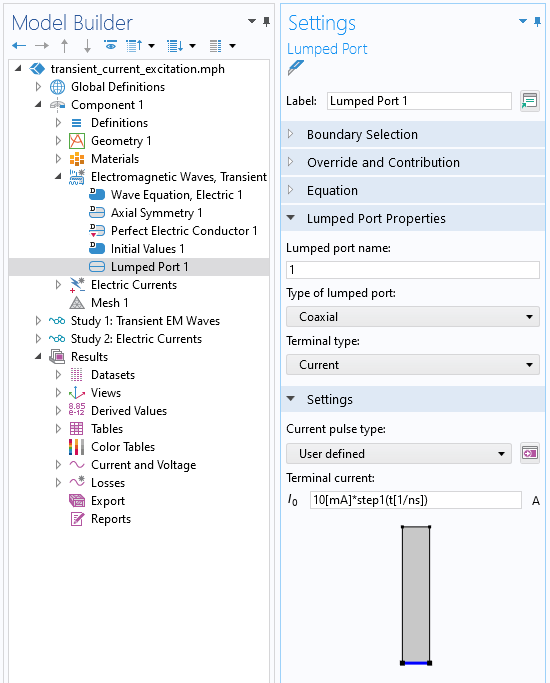
Capture d’écran de la condition limite Port réduit, de type Coaxial, utilisant un courant de pulsation variant dans le temps.
Nous utilisons la condition aux limites Port réduit, de type Coaxial, et spécifions un courant imposé transitoire. Notez que l’argument de la fonction Step est fourni sans unité. La durée totale de la simulation est de 150 ns, les résultats étant sauvegardés toutes les 1 ns. Le graphique ci-dessous montre la tension relevée sur la condition aux limites Port réduit (dans l’interface Ondes électromagnétiques, transitoire, qui est abrégée en TEMW dans la figure ci-dessous). La courbe illustre la réponse typique que l’on peut attendre d’un système résistif-capacitif.
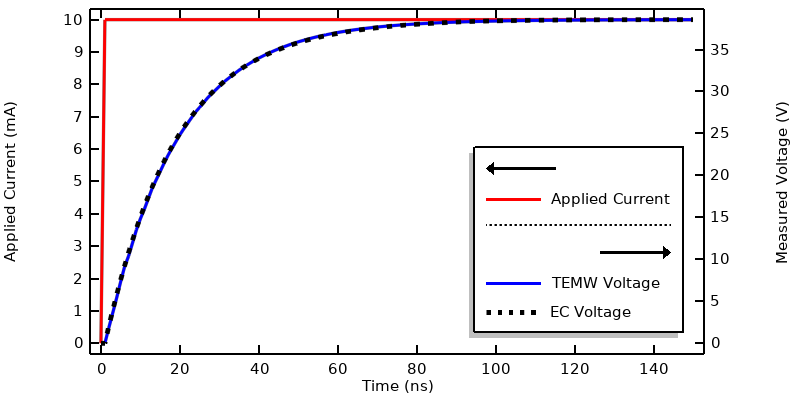
Tracé du courant imposé et de la tension calculée par l’interface Ondes électromagnétiques, transitoire et par l’interface Courants électriques.
On modélise la même situation avec l’interface Courants électriques, qui ne prend en compte que les effets résistifs et capacitifs. Dans cette interface, la condition aux limites Terminal de type Courant injectera le courant spécifié au niveau du conducteur interne. Sur le conducteur externe et les autres frontières externes, on applique la condition Masse. Pour comparer les solutions, le pas de temps maximal du solveur est également fixé à 1 ns. Les résultats montrent une excellente corrélation.
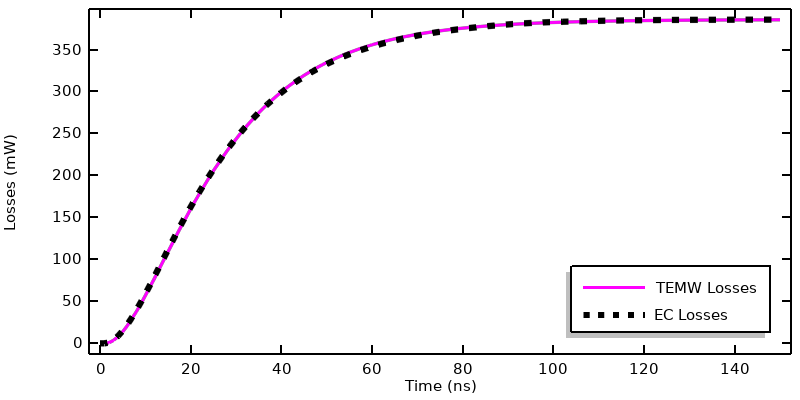
Comparaison de la dissipation calculée par l’interface Ondes électromagnétiques , transitoire et l’interface Courants électriques .
Ce graphique présente une comparaison de la chaleur produite dans le modèle en fonction du temps pour les deux interfaces physiques, et montre que les deux approches sont en accord. Nous pouvons également intégrer les pertes par rapport au temps à l’aide de l’opérateur timeint(), dont la syntaxe est la suivante :
timeint(0,150e-9, intopSample(ec.Qh), 'nointerp'),
où l’option 'nointerp' ajoutée évalue l’intégrale temporelle des pertes en utilisant uniquement les pas de temps stockés. Les deux interfaces calculent une énergie dissipée totale de 46,8 nJ sur cet intervalle de temps de 0 à 150 ns, avec moins de 1 % de différence. Sur la base de ces données, on peut conclure que pour un tel système excité par ce signal de courant, l’interface Courants électriques, donnera des résultats presque identiques à ceux de l’interface Ondes électromagnétiques, transitoire, et ce à moindre coût de calcul.
Excitations en tension des courants électriques
Ensuite, utilisons la même fonction Step, mais pour moduler la tension du Terminal dans l’interface Courants électriques. En d’autres termes, nous allons essayer de modifier instantanément la tension appliquée entre le conducteur interne et le conducteur externe du câble coaxial. Nous pouvons essayer de résoudre un tel modèle, mais cela conduira à un échec du solveur. On peut aisément le comprendre, puisqu’on serait dans le cas d’un dispositif capacitif devant résister à une variation instantanée de la tension. En d’autres termes, l’échelon de tension imposé n’est pas physique.
Au lieu d’essayer de résoudre une telle excitation non physique, nous pouvons revenir à la fonction Step et activer le lissage. Grâce à cette modification, nous pouvons résoudre le modèle sur une période plus courte de 5 ns, avec des résultats stockés toutes les 0.01 ns, et avec une tolérance relative du solveur plus stricte de 1e-5, comme décrit dans notre base de connaissances “ Controlling the Time-Dependent Solver Timesteps ”.
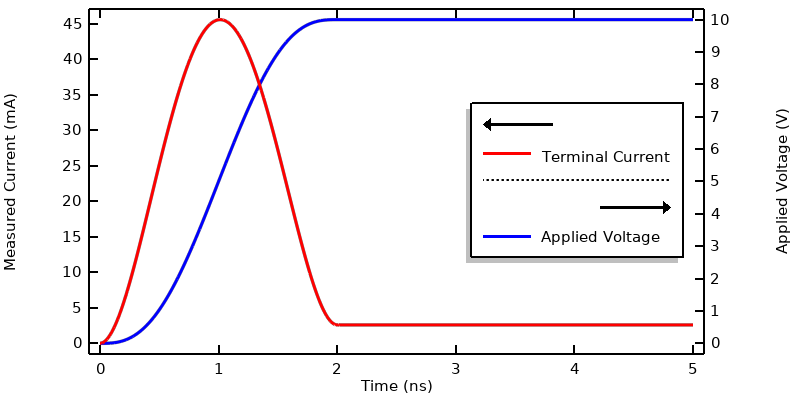
Courant calculé lorsque la tension est spécifiée par une fonction step lissée.
Ce graphique montre la tension imposée et le courant traversant le terminal. Notez qu’à mesure que la tension appliquée augmente, le courant augmente jusqu’à atteindre plus de dix fois la valeur du courant en régime stationnaire. Pour comprendre cela, examinons l’expression du courant, telle qu’elle est définie dans l’interface Courants électriques :
Il s’agit de la somme du courant de conduction et du courant de déplacement, le champ électrique étant calculé selon l’expression : . Ainsi, si le potentiel électrique en fonction du temps est spécifié sur une frontière, le courant de conduction et le courant de déplacement dans le modèle sont tous deux imposés, ce qui n’est pas physique. En revanche, dans le cas précédent d’un courant imposé, seul le courant total est spécifié et le modèle calcule quelle fraction de ce courant total est un courant de déplacement ou un courant de conduction.
Nous devrions également nous demander s’il est possible d’appliquer une condition limite similaire dans l’interface Ondes électromagnétiques, transitoires. Ce n’est pas possible ; cette interface utilise la formulation du potentiel vecteur magnétique, qui ne permet pas d’appliquer une telle condition d’excitation. Même si la méthode numérique le permettait, ce type d’excitation n’est pas physiquement réalisable car il impliquerait une sorte de boucle de rétroaction.
Il reste possible d’utiliser une excitation en tension dans l’interface Courants électriques dans le domaine temporel, mais uniquement lorsque le courant de déplacement résultant à la frontière du terminal est relativement bien plus faible que le courant de conduction. En d’autres termes, n’utilisez la condition limite de tension que dans les cas où le dispositif est quasiment purement résistif. Le cas que nous examinons ici, cependant, exige que nous nous tournions vers une condition aux limites plus réaliste.
Ligne de transmission, Port réduit et Terminal de type terminé
Examinons à nouveau la condition limite Port réduitdans l’interface Ondes électromagnétiques, transitoire. Le type Courant a déjà été abordé, et le type Circuit le sera plus tard. Nous allons donc nous concentrer sur le type Câble. L’option Câble permet de définir un signal de tension et une impédance de câble. Cela nous donne une condition interprétable comme une ligne de transmission infinie sans perte, d’impédance donnée, par exemple , avec une source placée le long du câble infini. Cette source impose un courant tel qu’un signal se propage dans les deux directions le long de la ligne de transmission en s’éloignant de la source, et tel que la tension mesurée sera égale au signal défini. Puisque le signal se propage dans les deux directions, l’intensité de ce courant imposé est de
.
Ce calcul est basé sur le signal de tension imposé, , et l’impédance de câble spécifiée &mdash ; en supposant que l’impédance du système corresponde à l’impédance du câble. En réalité, l’impédance du câble sera différente de l’impédance du système,
, de sorte que le signal sera partiellement réfléchi par le système et réinjecté dans la ligne de transmission. Le signal d’entrée est donc introduit par cette frontière en termes de tension, mais il impose en réalité un courant fixe ainsi qu’une charge en parallèle correspondant à l’impédance du câble. Nous pouvons considérer que le signal provenant de la source de courant est divisé entre le câble et le système, et qu’une fraction de ce signal est réfléchie. Dans la plupart des sources réelles, il y a une sorte de circulateur ou d’isolateur qui empêche le signal réfléchi d’interagir avec la source de courant, et qui détourne le signal réfléchi vers une charge dissipative adaptée.
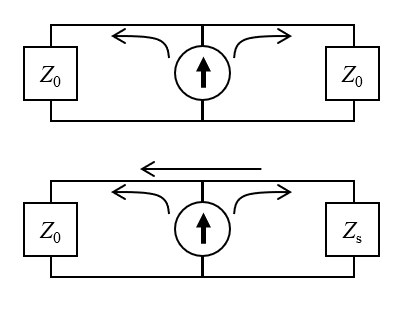
Interprétation en circuit équivalent de la condition limite Port réduit, de type Câble. La figure du haut présente le comportement présumé : le signal se propage depuis la source de courant dans le câble et le système, dont l’impédance est adaptée. La source se trouve à l’intérieur du câble, de sorte que le signal se propage dans les deux sens. La figure du bas montre le comportement modélisé : l’impédance non adaptée du système entraîne la réflexion d’une partie du signal dans le câble.
La condition limite analogue dans l’interface Courants électriques est la condition Terminal de type Terminé. Dans ce cas, nous pouvons également spécifier une impédance de câble, mais plutôt qu’une tension nous devons appliquer une puissance, qui s’exprime par .
Le modèle peut être résolu en utilisant des pas de temps de sortie plus fins et des tolérances plus faibles pour les deux physiques. Les résultats peuvent être évalués en termes de tension et de courant mesurés, ainsi que de pertes pouvant être intégrées dans le temps, comme indiqué ci-dessous. Plusieurs points méritent d’être soulignés :
- La tension et le courant obtenus à partir de l’interface Ondes électromagnétiques, transitoire présentent des ondulations dans le signal. Ce phénomène est normal. Ces ondulations sont dues à la composante fréquentielle du signal d’entrée et sont également dues aux réflexions du signal sur les matériaux, les conditions aux limites et la géométrie du système.
- La tension calculée est presque deux fois supérieure à la tension appliquée. Cela est dû au fait que cette condition limite peut également être considérée comme un équivalent de Norton d’une source de tension, mais avec une résistance de Norton égale à l’impédance du câble, qui, dans ce cas, est relativement faible par rapport à la résistance du système modélisé.
- La solution obtenue à partir de l’interface Courants électriques ne présente aucune ondulation puisque cette interface ignore explicitement les effets inductifs, mais la forme générale est très similaire et donne la même solution en régime permanent.
- Les pertes sont bien corrélées, et l’énergie totale dissipée correspond à 1% près.
Nous pouvons donc conclure que l’interface Courants électriques est une très bonne approximation de l’interface complète, Ondes électromagnétiques, transitoire, pour ce système et ce type d’excitation.
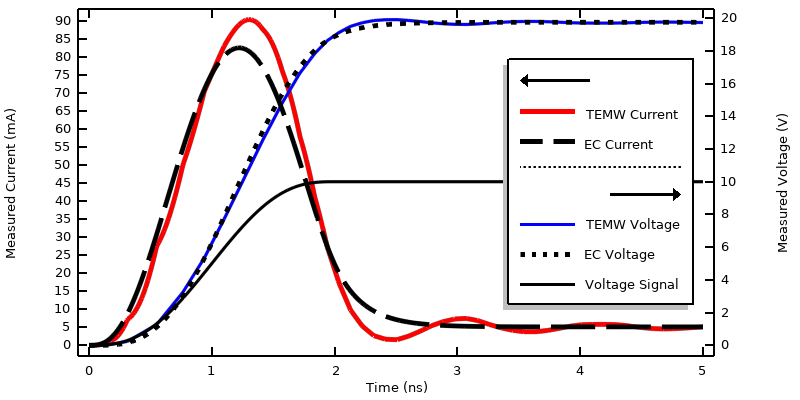
Graphique de la tension et du courant mesurés lors de la modélisation d’un signal de tension en step lissé se propageant le long d’une ligne de transmission.
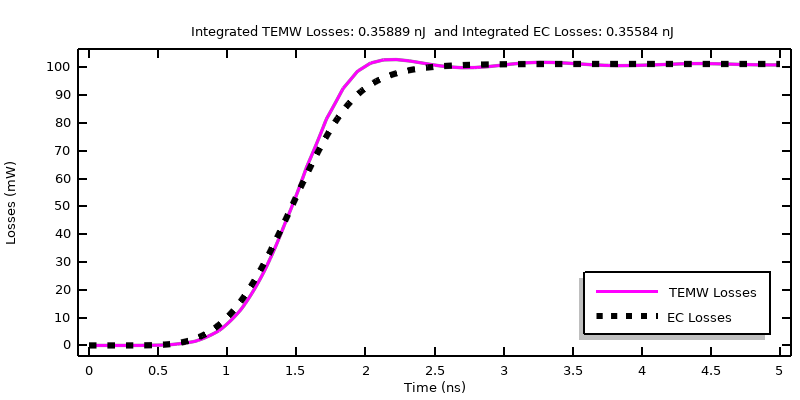
Comparaison des pertes calculées avec l’échantillon de matériau lorsqu’on applique un signal de tension suivant une fonction step lissée.
Connexions des circuits électriques
Si l’on examine le schéma de circuit de la figure précédente, on peut penser que le Port réduit, de type Câble, représente une résistance attachée au système. Nous pouvons vérifier cette interprétation en utilisant plutôt le Port réduit, de type Circuit, et en ajoutant une source de courant réduite et une résistance réduite en parallèle du système via l’interface Circuit électrique. L’approche consistant à connecter ces interfaces physiques est similaire à celle présentée dans notre article de blog “Understanding the Excitation Options for Modeling Electric Currents”. La même excitation peut être obtenue en connectant l’interface Courants électriques à l’interface Circuit électrique à l’aide d’une condition Terminal de type Circuit.
Un circuit adapté plus complexe, comprenant des condensateurs, des inducteurs et des transformateurs, pourrait également être mis en œuvre dans l’interface Circuit électrique. Dans cette interface, il est possible d’utiliser une source de tension à condition que des éléments supplémentaires soient ajoutés au circuit pour éviter toute forme d’excitation non physique. Les dispositifs non linéaires, les diodes et les transistors, peuvent également être introduits, bien que cela se traduise par un ensemble d’équations dont la résolution requiert plus de ressources de calcul et qui peut nécessiter une modification des paramètres du solveur.
Quelques mots sur la puissance dissipée
Dans l’article de blog traitant l’excitation dans le domaine fréquentiel de ce type de système, nous avions également mis en œuvre une excitation permettant d’injecter une puissance connue dans le système. Ce type d’excitation est rétroactive, ce qui signifie qu’elle suit un certain état du modèle et réinjecte l’information en entrée. Ce type de rétroaction se justifie dans un modèle en domaine fréquentiel, si l’on suppose implicitement que la rétroaction s’effectue sur plusieurs cycles. Elle a beaucoup moins de sens dans un modèle temporel, où toute rétroaction devrait également inclure la dynamique et le retard du système de contrôle. Elle n’est donc pas applicable à des systèmes et des échelles de temps similaires à ceux que nous étudions ici.
Conclusion
Nous avons examiné diverses façons d’exciter un système avec un signal temporel dans l’interface Courants électriques et dans l’interface Ondes électromagnétiques, transitoire. Pour le système et le signal considérés, ces deux interfaces produisent des résultats très similaires. L’interface Courants électriques convient lorsque l’énergie électrique dans le système excité est beaucoup plus importante que l’énergie magnétique. Dans un prochain article, nous aborderons l’autre cas, à savoir lorsque le système est principalement inductif et que les champs magnétiques sont beaucoup plus importants que les champs électriques.
Nous avons vu que toutes les excitations reviennent, en fait, à imposer le courant entrant dans le système. Le cas d’un signal de tension se propageant le long d’une ligne de transmission est simplement un équivalent de Norton : une source de courant avec une résistance externe – représentant la ligne de transmission – en parallèle du système. En fin de compte, le choix entre ces options d’excitation représentant une source de courant, un signal de tension se propageant le long d’une ligne de transmission, ou l’ajout d’une interface Circuit électrique dépend de la nature de la source avec laquelle vous travaillez.
Les signaux étudiés ici sont assez simples, mais nous devons souvent prendre en compte des signaux transitoires plus compliqués, et en particulier des signaux périodiques. De tels signaux font l’objet de techniques de modélisation avancées, qui seront abordées dans un prochain article. A suivre donc !




Commentaires (0)