Minimisation des contraintes: une approche heuristique pour améliorer le comportement en fatigue

Pour estimer la fatigue, de nombreuses mesures sont basées sur l’évaluation des contraintes mécaniques; cependant, celles-ci sont incompatibles avec les méthodes d’optimisation de haute performance telles que l’optimisation par gradient. Il est donc difficile d’améliorer les performances en fatigue en appliquant les méthodes d’optimisation de façon directe. Ce blog montre comment la minimisation des contraintes peut être utilisée en tant qu’approche heuristique pour améliorer le comportement en fatigue. Cette approche s’appuie sur l’optimisation par gradient pour améliorer des milliers de variables de conception tout en conservant les caractéristiques de masse et de rigidité.

Comprendre le phénomène de fatigue

Lorsqu’une pièce est soumise à des efforts de façon répétée, de petites fissures peuvent se développer dans le matériau. Ces fissures commencent ensuite à s’agrandir à chaque cycle d’effort, jusqu’à ce que la propagation entre dans une phase rapide, conduisant à la rupture finale de la pièce. Cette succession de phénomènes, comprenant l’initiation, la propagation et la rupture finale, définit le processus de rupture par fatigue. En pratique, dans la plupart des cas, l’objectif est d’empêcher complètement l’apparition d’une fissure, car contrôler la phase de propagation une fois qu’une fissure est amorcée est une tâche ardue. L’objectif d’une analyse de fatigue est de calculer le nombre de cycles d’effort que la pièce peut tolérer jusqu’à ce que cela se produise. Ce nombre définit la durée de vie en fatigue.

Le de Havilland Comet était un avion qui s’est fracturé en plein vol en raison de fissures causées par de la fatigue au niveau des perçages des rivets situés près des hublots. Pour éviter que cela ne se reproduise, les versions ultérieures de l’avion ont utilisé des hublots fixés avec de la colle. Image par Completeaerogeek. Sous licence CC BY-SA 4.0, via Wikimedia Commons.

L’apparition de fissures de fatigue dépend de l’effort exercé sur la pièce et des contraintes qu’il génère. Il convient de noter que les fissures de fatigue peuvent apparaître à des niveaux de contraintes bien inférieurs à la limite d’élasticité du matériau et que la répétitivité de l’effort est l’un des principaux facteurs d’apparition des fissures de fatigue. Du point de vue de la conception, cependant, il peut être utile de ne pas tenir compte du comportement cyclique de l’effort et, à la place, de considérer un cas de chargement statique afin d’identifier les endroits où les contraintes sont élevées.

Minimisation des contraintes

La minimisation de la contrainte maximale est un objectif courant en mécanique des structures, mais en pratique ce type de problèmes d’optimisation est difficile à résoudre car l’emplacement précis de la contrainte maximale peut changer au cours de l’optimisation. Il est donc courant d’utiliser des techniques d’agrégation de contraintes qui approchent la contrainte maximale, comme tout particulièrement la norme p de la contrainte de von Mises:

La précision de l’approximation s’améliore à mesure que p\rightarrow\infty, mais cela entraîne également une variation plus soudaine du gradient, ce qui pose des problèmes numériques. Par conséquent, les valeurs supérieures à 10 sont rarement utilisées pour l’optimisation topologique. Ce blog se concentre cependant sur l’optimisation de forme où des valeurs plus grandes, jusqu’à 50, peuvent parfois être utilisées sans introduire de problèmes numériques. La contrainte maximale approximative, \sigma_\mathrm{max}, et ses variantes peuvent être utilisées pour contraindre les contraintes mécaniques dans l’optimisation de forme et l’optimisation topologique, comme le montre la bibliothèque d’applications de COMSOL^® (par exemple, dans les modèles Optimisation d’un profil de volant d’inertie et Optimisation topologique d’une structure coudée avec pour contrainte d’optimisation le maximum de contrainte mécanique). Dans les exemples suivants, nous montrerons que cet objectif peut être utilisé comme approche heuristique pour l’optimisation de forme en fonction du comportement en fatigue.

Résultats pour un bracket

Le premier exemple est une géométrie de bracket, utilisée pour illustrer différents aspects de mécanique des structures. (Pour plus d’informations, se référer au tutoriel Bracket — Optimisation des contraintes par évaluation de la fatigue.) L’image ci-dessous représente les conditions de chargement et les conditions aux limites, ainsi que la distribution des contraintes. Des ressorts sont utilisés sur les perçages de fixation afin d’éviter des concentrations de contraintes artificielles. Le modèle peut également être étoffé en incluant les boulons.

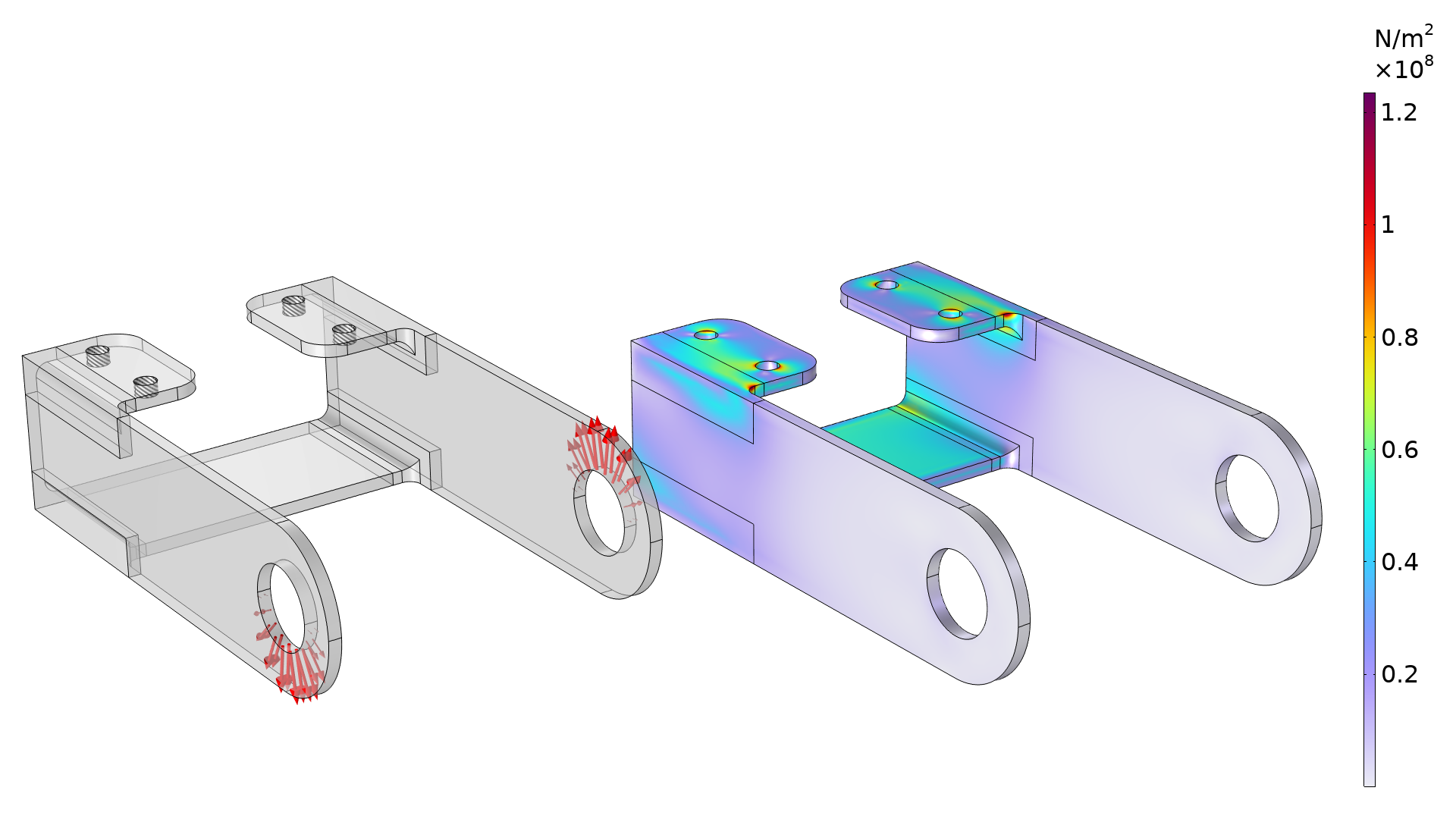
Le graphique montre les conditions limites (à gauche) et la distribution de contraintes initiale (à droite). Les contraintes sont concentrées aux abords des congés dans la partie supérieure du bracket.

L’optimisation utilise la norme p (p=50), mentionnée dans la section précédente comme fonction objectif. Des contraintes d’optimisation sont également ajoutées pour éviter d’obtenir une structure plus lourde ou moins rigide. Les exemples 3D considérés ici utilisent la fonctionnalité Frontière de forme libre, mais le logiciel COMSOL Multiphysics^® propose une variété de fonctionnalités prédéfinies pour l’optimisation de forme, comme expliqué dans notre blog “Optimisation de forme en électromagnétisme: Partie 1”. Utiliser la fonctionnalité Frontière de forme libre modifie la forme du congé problématique pour atténuer la concentration de contraintes, améliorant ainsi les caractéristiques de fatigue (comme illustré ci-dessous).

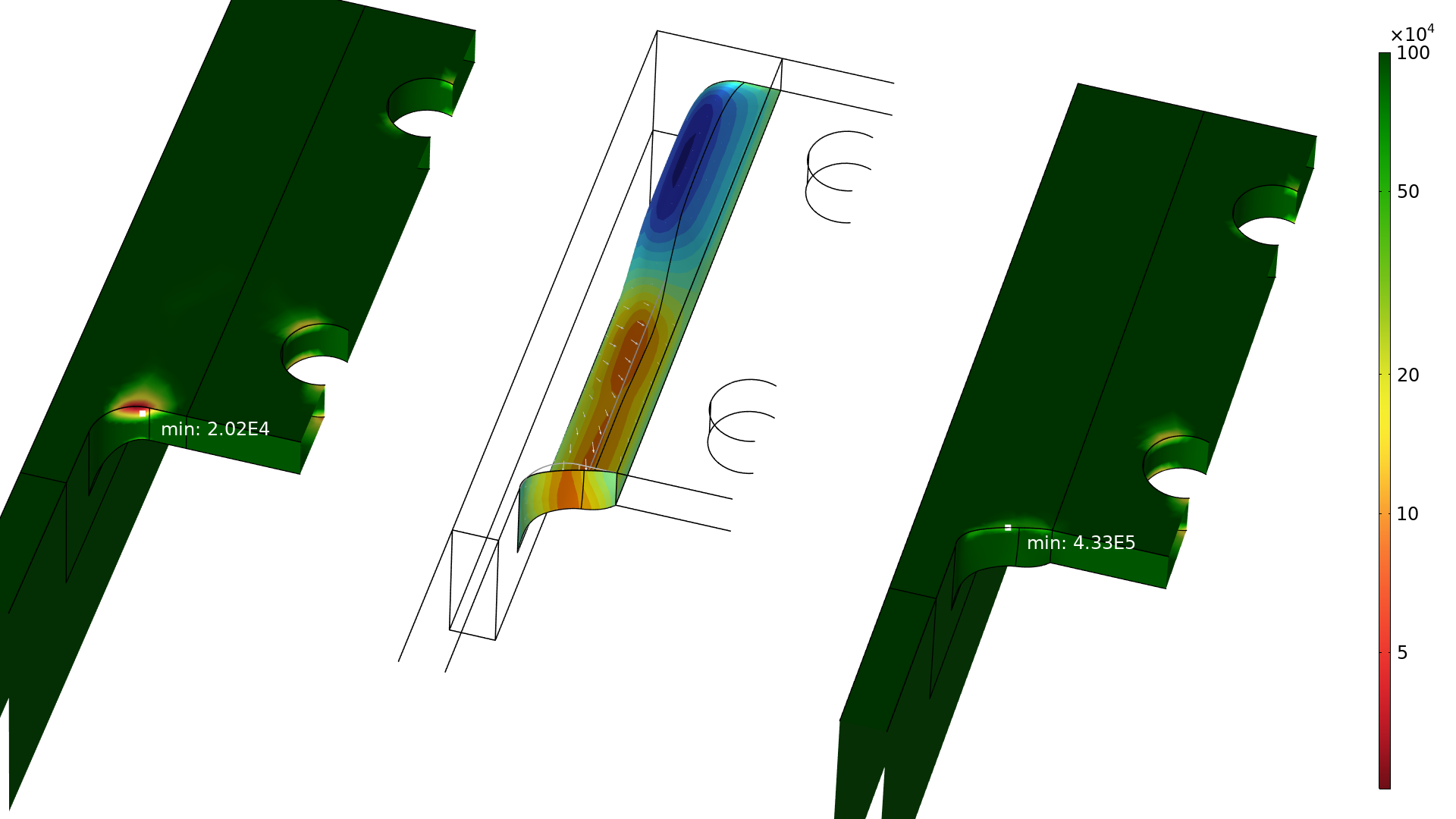
Le nombre de cycles à la rupture est représenté sur des coupes de la géométrie initiale et de la géométrie optimisée (à gauche et à droite, respectivement). Le changement de forme est également illustré par les flèches sur l’image du milieu, où les régions bleue et rouge correspondent respectivement à du retrait et à de l’ajout de matière.

En général, un composant va rompre dès que la durée de vie en fatigue est dépassée dans l’une de ses parties, et le résultat le plus pertinent est donc le nombre minimum de cycles à la rupture. Dans l’idéal, il faudrait l’utiliser directement comme fonction objectif, mais on constate une bonne corrélation entre ce nombre et la norme p en tant que fonction objectif, comme montré dans le graphique ci-dessous.

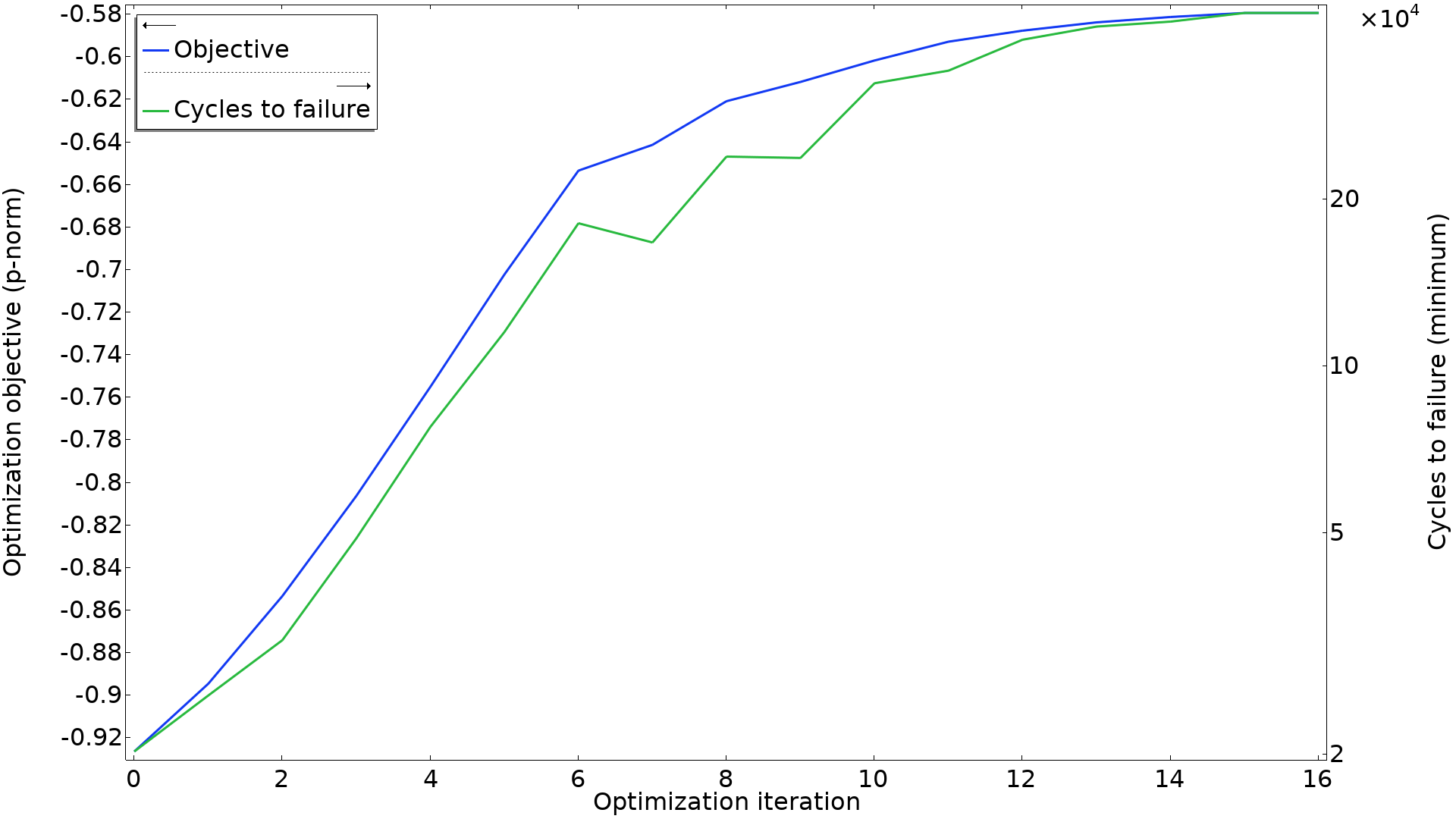
La norme p comme fonction objectif est représenté en même temps que le nombre minimum de cycles à la rupture. Certaines itérations améliorent la norme p sans améliorer le nombre minimum de cycles à la rupture, mais on constate une bonne corrélation entre les deux.

Contraintes de Von Mises et durée de vie en fatigue

Comment expliquer le fait que minimiser les contraintes de von Mises soit si bien corrélé à une amélioration de la durée de vie en fatigue ? La durée de vie en fatigue d’un composant est affectée par de nombreux facteurs, la plage de contraintes étant le principal contributeur. Elle est également fortement influencée par la contrainte moyenne. Dans le cas courant où les efforts sont complètement réversibles, la contrainte moyenne est nulle partout.

Les fissures de fatigue prennent généralement naissance sur une surface libre, au niveau d’une zone de concentration de contraintes. Sur une surface libre, un état de contraintes planes prévaut, mais dans la pratique, il est courant que l’état de contrainte soit presque uniaxial. Cela signifie par exemple que la première contrainte principale et la contrainte équivalente de von Mises seront identiques.

Dans la situation où vous avez à la fois un chargement de forme statique générant une contrainte moyenne et un autre chargement de forme impulsionnelle, cette approche n’est pas nécessairement optimale. Cependant, même dans cette situation, les chances de succès sont importantes car s’il y a une concentration de contraintes, des chargements de forme différente entraînent souvent des répartitions de contraintes similaires.

Résultats pour une roue

Le second exemple que nous allons étudier est une jante, reprise du modèle Jante — Optimisation de contraintes avec évaluation de la fatigue. Ce modèle est conceptuellement identique au bracket, à l’exception de quatre aspects:

1. Il y a plusieurs cas de chargement et l’analyse en fatigue recherche la combinaison la plus défavorable (en utilisant le critère de Findley), de sorte que l’on s’attende à une corrélation plus faible avec la contrainte maximale.
2. Le fait qu’il y ait un plus grand nombre de cas de chargement augmente le nombre de contraintes d’optimisation.
3. La périodicité angulaire est imposée pour l’optimisation de forme (pas pour la physique).
4. Le facteur d’usage est utilisé dans les résultats (au lieu de la durée de vie en fatigue) et peut être considéré réciproquement comme un coefficient de sécurité.

La géométrie de la roue, les contraintes d’optimisation et les conditions limites sont illustrées ci-dessous. De simples conditions limites d’encastrement sont utilisées pour les boulons, donnant lieu à des concentrations de contraintes artificielles, ces zones sont donc exclues de l’analyse en fatigue.

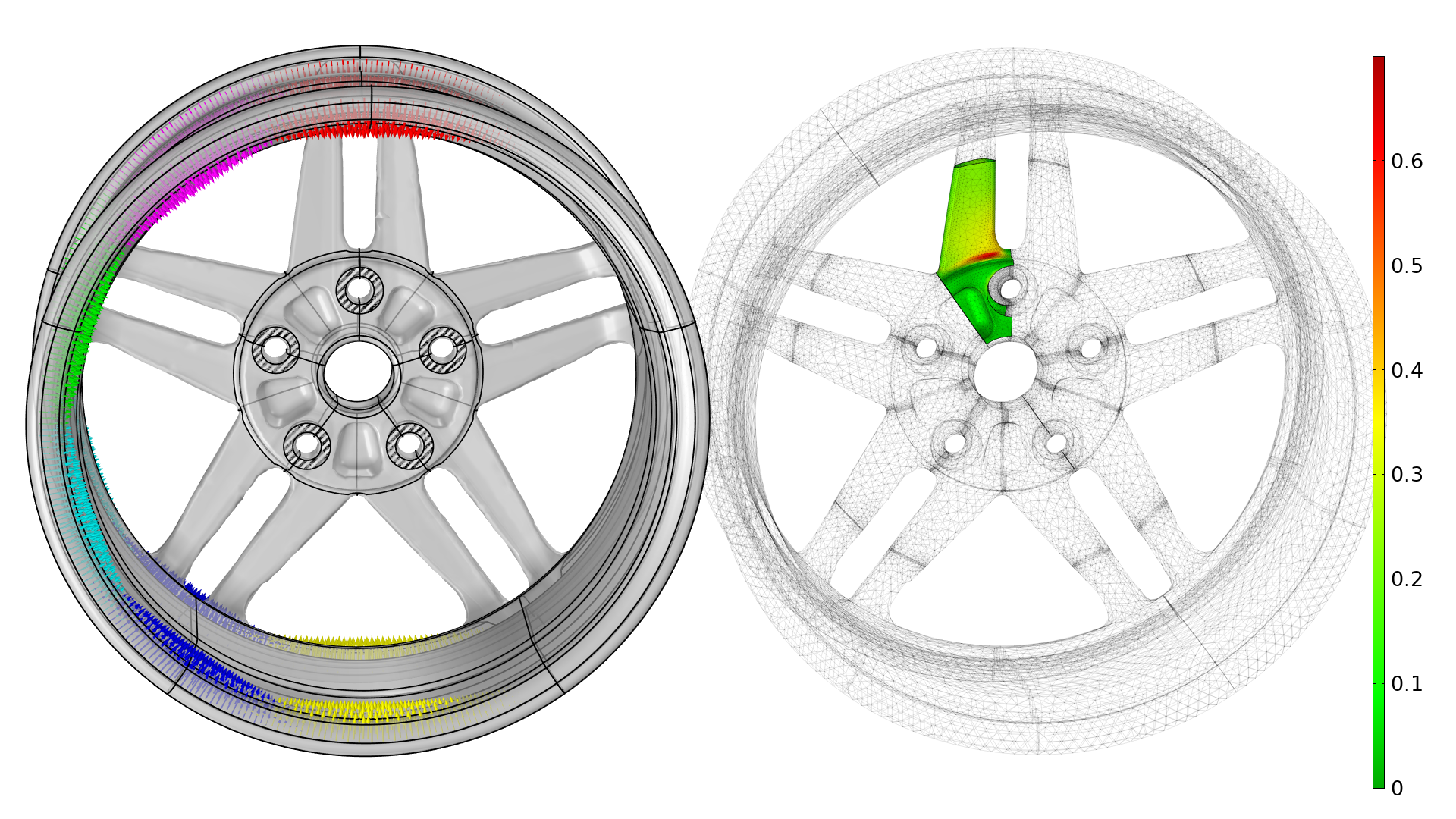
Les différents cas de chargement sont illustrés par des flèches de différentes couleurs (à gauche). Le facteur d’usage initial est affiché à droite, prenant en compte tous les cas de chargement, ce qui correspond à un tour complet de la roue. Notez qu’un maillage grossier peut être utilisé pour les rayons, mais pas pour évaluer la fatigue ou les contraintes mécaniques. La roue subit également un effort issu de la pression d’air du pneu, mais celui-ci est exclu de la modélisation.

L’optimisation utilise encore la norme p comme fonction objectif (p=20) ainsi qu’une contrainte d’optimisation sur la masse, mais cet exemple prend en compte davantage de cas de chargement, et donc davantage de contraintes d’optimisation. Les images ci-dessous illustrent comment l’optimisation améliore la durée de vie en fatigue en modifiant un congé.

Le facteur d’usage est représenté sur les coupes des géométries initiale et optimisée (respectivement à gauche et à droite). Le changement de forme est également schématisé par des flèches dans l’image du milieu, où les lignes grises et noires indiquent respectivement la géométrie initiale et la géométrie optimisée.

Cet exemple présente également une bonne corrélation entre la norme p comme fonction objectif et le nombre minimum de cycles à la rupture, comme montré dans le graphique ci-dessous. Il est intéressant de noter que deux des cas de chargement contribuent de façon dominante sur la norme p, mais que toutes les contraintes d’optimisation demeurent actives tout au long de l’optimisation.

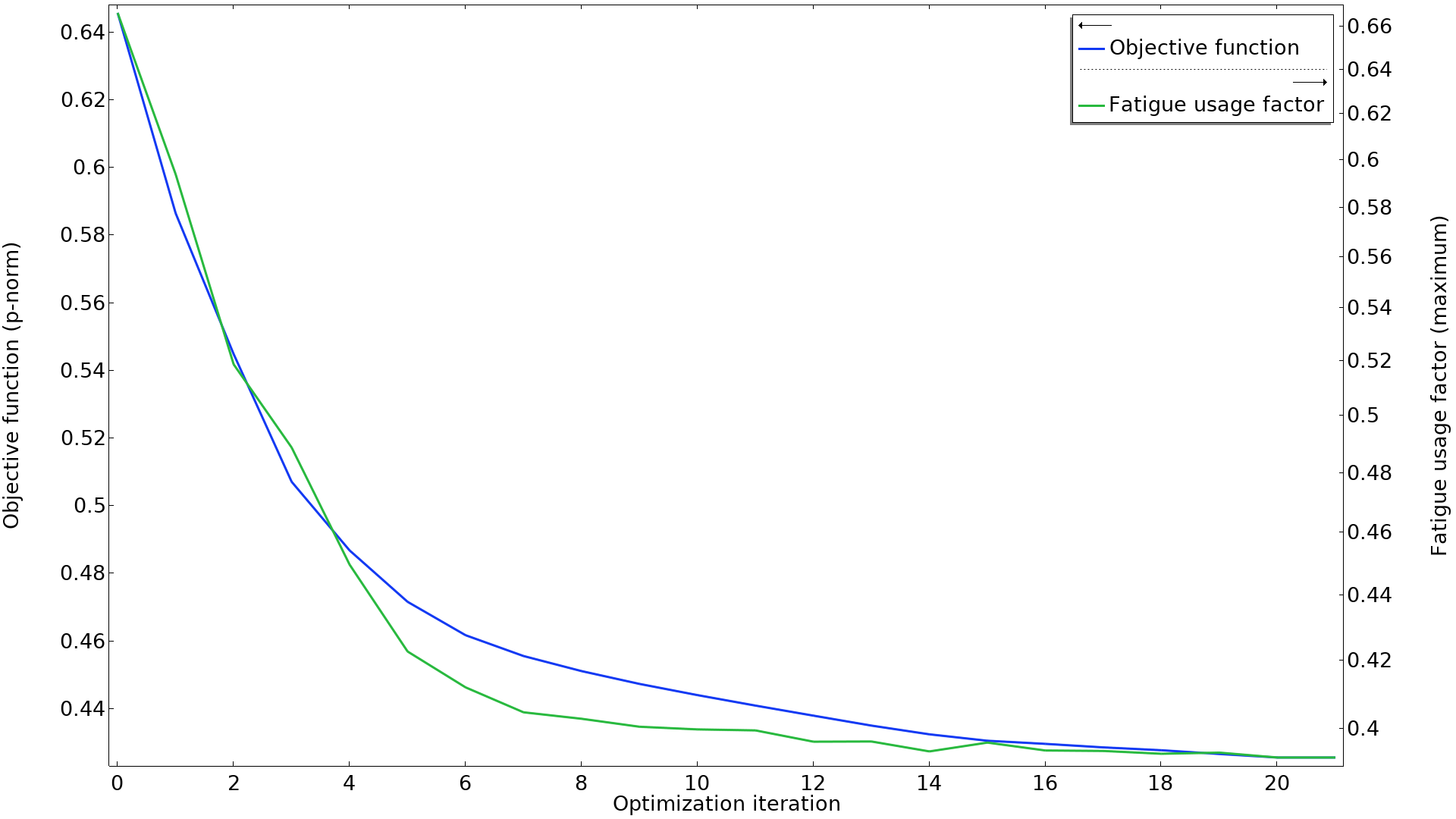
La norme p comme fonction objectif est tracée avec le facteur d’usage maximum. Les deux courbes semblent être bien corrélées. Notez que le facteur d’usage est tracé sur une échelle logarithmique.

Conclusion

L’optimisation de la durée de vie en fatigue n’est pas évidente, mais il est souvent possible d’améliorer le comportement en fatigue en réalisant une optimisation de forme par rapport aux contraintes mécaniques. Les résultats de l’optimisation doivent être vérifiés à l’aide d’une analyse en fatigue. Ces résultats peuvent être utilisés comme données d’entrée pour la suite du workflow.

Dans ce blog, nous nous sommes concentrés sur l’utilisation de la norme p de la contrainte de von Mises comme fonction objectif, mais comme COMSOL Multiphysics^® effectue automatiquement l’analyse de sensibilité nécessaire pour l’optimisation par gradient, on peut aisément expérimenter avec d’autres fonctions objectif.