
L’une des questions les plus courantes que nous recevons est la suivante : Quelle taille de modèle pouvez-vous résoudre avec le logiciel COMSOL Multiphysics®; ? Bien qu’à un certain niveau, il soit très facile de répondre à cette question, elle conduit inévitablement à une conversation plus longue sur les méthodes numériques, les stratégies de modélisation et les algorithmes de résolution, les performances du matériel informatique ainsi que sur la meilleure façon d’aborder les problèmes exigeants en ressources de calcul. Plongeons-nous dans ce sujet.
Note de l’éditeur : la version originale de ce billet a été publiée le 24 octobre 2014. Elle a depuis été mise à jour pour refléter les nouvelles caractéristiques et fonctionnalités.
Examinons quelques données
Nous allons commencer par mettre en place un modèle tridimensionnel pour la distribution de la température en régime permanent dans un domaine et allons étudier les besoins en mémoire et le temps de résolution avec un nombre croissant de degrés de liberté (DDL). En d’autres termes, le modèle est résolu sur des maillages de plus en plus fins en utilisant le solveur par défaut sur une station de travail de bureau typique, en l’occurrence un processeur Intel® Xeon® W-2145, avec 32 Go de RAM et un disque SSD.
Nous allons tout d’abord examiner les besoins en mémoire à mesure que la taille du modèle augmente en termes de deux quantités évaluées : la mémoire virtuelle et la mémoire physique. La mémoire virtuelle est la quantité de mémoire que le logiciel demande au système d’exploitation (OS). (Ces données proviennent d’une machine Windows® la gestion de la mémoire sur tous les systèmes d’exploitation pris en charge est très similaire). La mémoire physique est la quantité de mémoire RAM qui est occupée. La mémoire physique sera toujours inférieure à la fois à la mémoire virtuelle et à la quantité de RAM installée, puisque le système d’exploitation, ainsi que les autres programmes exécutés sur l’ordinateur, devront également occuper une certaine fraction de la RAM. Il existe un état où l’espace disponible dans la RAM physique est épuisé, et où une fraction significative des données transite par le SSD. Il existe également un état au-delà duquel le logiciel signale qu’il n’y a pas assez de mémoire et que le modèle ne peut donc pas être résolu du tout. Il est clair que l’ajout de d’une quantité de mémoire complémentaire à notre ordinateur nous permettrait de résoudre un modèle de taille plus importante, et nous pouvons extrapoler linéairement pour prédire les besoins en mémoire.
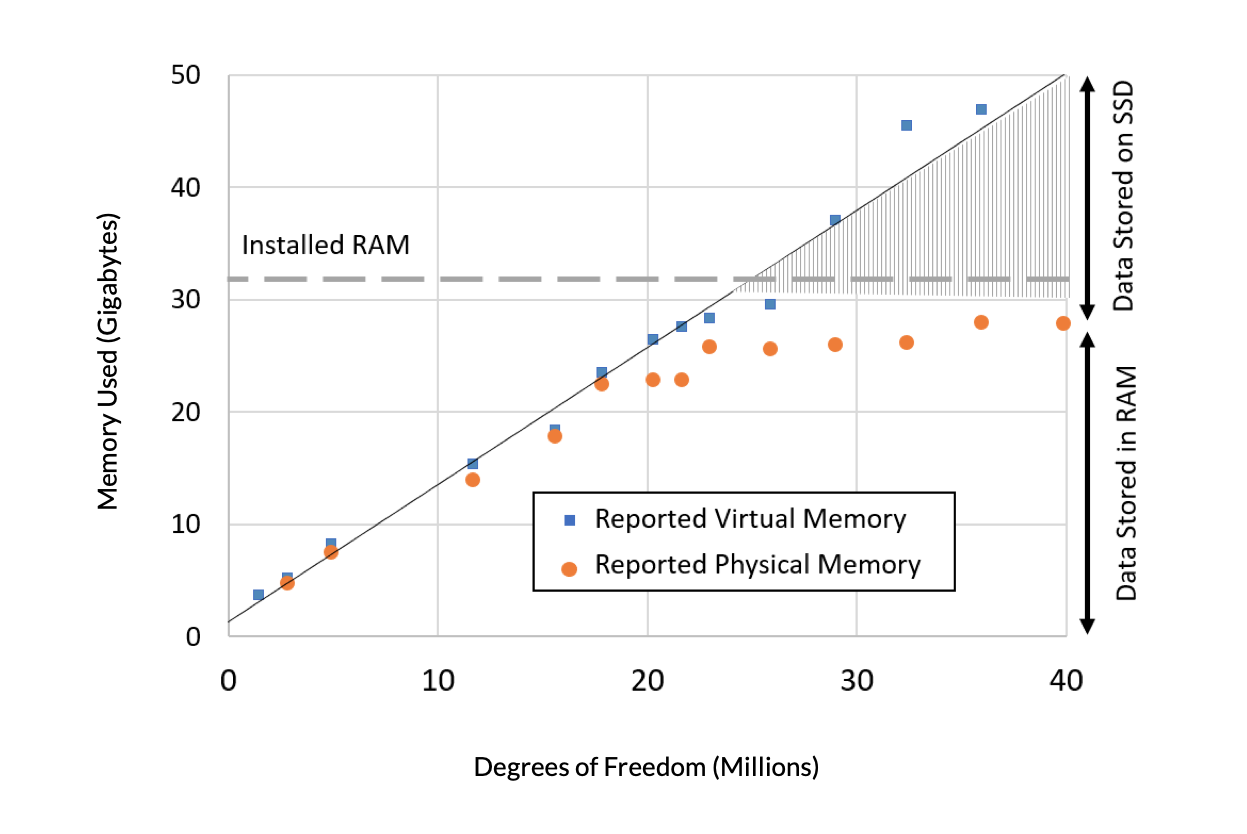
Figure 1. Mémoire virtuelle (bleu) et mémoire physique (orange) nécessaires en fonction de la taille du problème, en termes de millions de DDL, pour un modèle de transfert de chaleur dans des solides. Un ordinateur avec 32 Go de RAM a été utilisé.
Ensuite, examinons le temps de résolution de ce problème en fonction, encore une fois, des degrés de liberté. Le temps de résolution présente deux régions distinctes. Un polynôme du second ordre est ajusté à la région où la quantité de mémoire virtuelle nécessaire est inférieure à la RAM installée, et cette courbe est presque linéaire. Un autre polynôme du second ordre est ajusté aux données restantes, où la mémoire virtuelle est supérieure à la RAM installée. Cette courbe présente une pente plus raide car, dans ce régime, il faut plus de temps pour accéder aux données du modèle stockées dans la mémoire virtuelle.
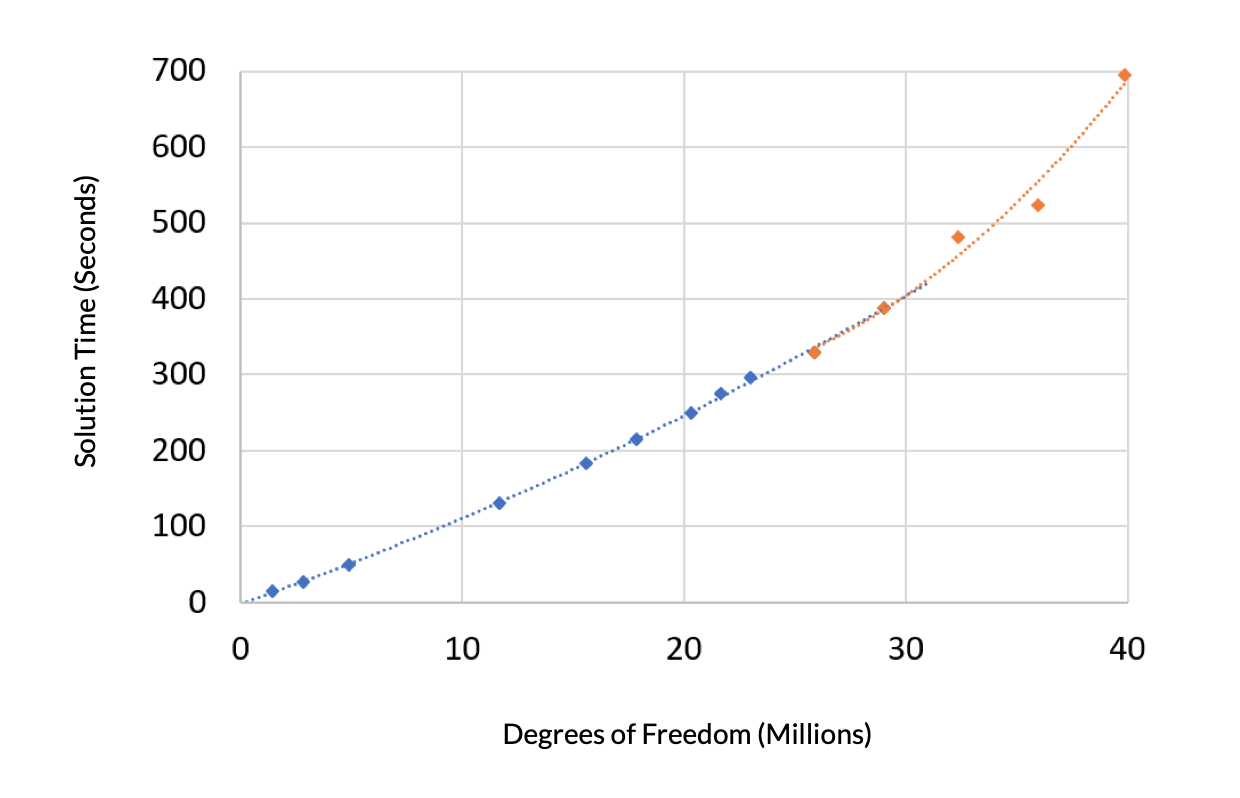
Figure 2. Le temps de résolution en fonction du nombre de DDL présente une pente plus forte lorsque la taille du problème est supérieure à la RAM disponible.
Les besoins en mémoire seront-ils toujours les mêmes ?
Nous pouvons raisonnablement nous demander si les données précédentes concernant les besoins en mémoire seront toujours vraies. Comme vous l’avez probablement deviné, la réponse est non, les données ont très peu de valeur prédictive, sauf pour des problèmes très similaires.
6 Modifications typiques apportées aux modèles
Quels sont les changements courants que nous pourrions apporter au modèle actuel et qui entraîneraient un déplacement de ces courbes vers le haut ou vers le bas ? Nous couvrons plusieurs exemples différents ci-dessous.
1. Résolution dans le domaine temporel
La résolution d’un problème dans le domaine temporel, à l’aide d’un solveur temporel, nécessitera le stockage de plus de données en mémoire par rapport à la résolution d’un problème en régime permanent. Pour une vue d’ensemble des algorithmes, lisez notre billet de blog “Automatic Time Step and Order Selection in Time-Dependent Problems”.
2. Changement du type de solveur linéaire
Le problème mentionné ci-dessus pourrait être résolu à l’aide de solveurs itératifs ou directs. Les solveurs itératifs utiliseront beaucoup moins de mémoire que les solveurs directs, surtout lorsque la taille du problème augmente. Les solveurs directs ne sont justifiés que pour certains types de problèmes, par exemple lorsque la matrice du système est assez mal conditionnée en raison de forts contrastes dans les propriétés des matériaux, par exemple, mais qu’elle évolue quand même de façon superlinéaire.
3. Introduction d’une non-linéarité
Même au sein d’une même physique, l’introduction de tout type de non-linéarité, comme faire en sorte que les propriétés matériaux soient fonction de la température, peut résulter en une matrice du système non-symétrique. Cela augmentera les besoins en mémoire. Il est possible d’éviter cela en utilisant l’opérateur nojac() afin d’éviter la dérivation symbolique, bien qu’il ne soit pas souhaitable de le faire dans tous les cas, car cela peut avoir un effet négatif sur le taux de convergence non-linéaire.
4. Changer le type d’élément
Le type d’élément par défaut pour un problème tridimensionnel est l’élément tétraédrique, mais un autre type d’élément pourrait également être utilisé, comme un prismatique triangulaire ou un hexaédrique. Ces éléments ont une plus grande connectivité par élément et augmentent l’utilisation de la mémoire. D’autre part, le changement de type d’élément peut être fortement motivé pour certaines géométries et types de problèmes car ils peuvent conduire à des maillages beaucoup plus grossiers pour la même géométrie, notamment lorsqu’ils sont combinés avec le partitionnement de la géométrie et les maillages extrudés.
5. Changer l’ordre des éléments
L’ordre des éléments par défaut lorsque l’on résout un cas de Transfert de chaleur dans des solides est Lagrange quadratique. Changer pour un ordre linéaire diminuera le nombre de degrés de liberté dans le modèle si le maillage est le même et conduira également à ce que chaque élément ait moins de connectivité. En d’autres termes, chaque nœud de chaque élément a moins de nœuds voisins avec lesquels communiquer. Cela conduit à une utilisation de la mémoire plus faible pour le même nombre de DDL. De façon opposée, l’augmentation de l’ordre des éléments entraîne une plus grande connectivité, ce qui conduit à une plus grande utilisation de mémoire pour le même nombre de DDL. En outre, il est possible de passer d’un élément de Lagrange à un élément Serendip, ce dernier ayant moins de nœuds par élément. Il faut toutefois comprendre que la modification de l’ordre et du type d’éléments a des effets à la fois sur la précision et sur les exigences en matière de maillage géométrique, ce qui est un sujet compliqué en soi; il convient donc de faire preuve de prudence lorsqu’on modifie l’ordre des éléments par rapport à l’ordre par défaut.
6. Introduction de couplages non locaux ou d’équations globales
Un couplage non local implique tout type de termes de couplage supplémentaires qui transmettent des informations entre des éléments non voisins et sont souvent utilisés en conjonction avec des équations globales. Leur utilisation affecte la quantité d’informations dans la matrice du système et rend souvent le problème non linéaire. Certaines conditions aux limites, telles que la condition aux limites de Terminal, sont disponibles pour les problèmes impliquant des courants électriques et introduisent des couplages non locaux ou des équations globales en arrière-plan. Les couplages non locaux peuvent également être implémentés manuellement, comme expliqué dans notre billet de blog “Computing and Controlling the Volume of a Cavity”.
Résoudre différentes physiques
Qu’en est-il si vous résolvez une physique différente ? L’exemple mentionné ci-dessus concernait la modélisation du transfert de chaleur, où la méthode des éléments finis (MEF) est utilisée pour résoudre le champ de température (scalaire). Si vous résolvez une physique différente via la MEF, vous pouvez alors résoudre un champ vectoriel. Par exemple :
- Mécanique du solide
- L’interface Mécanique du solide résout le champ de déplacement dans l’espace 3D, donc pour le même maillage, il y aura trois fois plus de degrés de liberté, et plus de connectivité entre éléments, par rapport au problème thermique. Pour certains problèmes de mécanique des solides impliquant des solides incompressibles, la résolution supplémentaire de la pression augmentera encore plus les besoins en mémoire. Introduire des lois de comportement non-linéaires peut encore augmenter les besoins en mémoire en fonction de la loi de comportement utilisée.
- Ecoulements fluides
- Les interfaces concernant les Ecoulements fluides résolvent toutes le champ de vitesse en 3D ainsi que la pression. Lorsque l’on résout un écoulement turbulent, au moins une variable de turbulence supplémentaire est résolue. Lorsque l’on résout un écoulement multiphasique, il y a au moins une variable supplémentaire qui suit la phase.
- Electromagnétisme
- Selon les équations qui vous intéressent, vous pourriez résoudre une équation scalaire ou une équation vectorielle, ou même ajouter une équation additionnelle de fixation de jauge.
- Transport d’espèces chimiques
- Lors de la résolution de problèmes de génie chimique, tels que des écoulements réactifs, le nombre de degrés de liberté est proportionnel au nombre d’espèces chimiques que vous incluez dans le modèle.
Gardez à l’esprit que pour chacune de ces physiques, ou toute autre physique résolue via la MEF, nous devons à nouveau considérer l’effet de tous les points mentionnés précédemment. Qu’en est-il si nous regardons au-delà de la MEF ? Il y a des interfaces et des méthodes au sein de COMSOL® que nous pouvons utiliser, comme l’interface Suivi de particules, qui résout un ensemble d’équations différentielles ordinaires (EDO) pour la position des particules et a des besoins en mémoire beaucoup plus faibles en fonction du nombre de degrés de liberté que la MEF ; l’interface Optique géométrique, qui résout également un ensemble d’EDO et a des besoins en mémoire similaires à ceux du suivi de particules ; les approches Galerkin discontinues (dG) &mdash ; qui sont utilisées pour résoudre des modèles d’ondes électromagnétiques, d’ondes acoustiques et élastiques — utilisent très peu de mémoire par rapport à MEF ; et, enfin, la méthode des éléments de frontière (BEM), qui est une méthode de discrétisation, mais sur des frontières plutôt que des volumes. Cela entraîne des besoins en mémoire beaucoup plus élevés pour chaque degré de liberté par rapport à la MEF, mais moins de degrés de liberté sont nécessaires pour obtenir la même précision. Elle est mise en œuvre pour l’acoustique, l’électrostatique, la distribution de courant, la magnétostatique et les ondes électromagnétiques.
Enfin, vous avez non seulement la possibilité d’inclure ces différentes physiques dans votre modèle, mais vous pouvez également les inclure de façon combinée pour construire un véritable modèle multiphysique. Dans ce cas, vous devez également tenir compte des approches de résolution possibles, car ces modèles peuvent être résolus à l’aide d’une approche fortement couplée ou ségrégée, et de solveurs directs ou itératifs, ce qui a une incidence sur les besoins en mémoire. Le tableau ci-dessous donne une idée approximative des besoins en mémoire pour certaines interfaces de physique typiques, pour des problèmes typiques dans ces domaines.
| Physique | Degrés de liberté par gigaoctet |
|---|---|
| Transfert de chaleur dans des solides | 800,000 |
| Mécanique du solide | 250,000 |
| Ondes électromagnétiques | 180,000 |
| Ecoulement laminaire | 160,000 |
À ce stade, vous avez, je l’espère, une idée de la complexité de la prévision des besoins en mémoire. Mais d’un point de vue pratique, à quoi servent toutes ces informations ? Pour votre travail quotidien, cela se résume à une chose : vous devrez effectuer une étude de scalabilité. Cela implique de commencer par un petit modèle qui fait appel à toutes les physiques, les conditions aux limites et les couplages, et qui utilise la discrétisation souhaitée. Commencez par résoudre ce modèle et augmentez progressivement le nombre de degrés de liberté tout en surveillant les besoins en mémoire. Ces données seront généralement linéaires, mais peuvent parfois croître proportionnellement au carré du nombre de degrés de liberté, comme dans le cas de l’utilisation de la BEM avec un solveur direct ou s’il existe certains types de couplages non locaux. Une fois que vous disposez de ces informations, vous êtes prêt à passer à l’amélioration des performances du modèle.
Comment un matériel informatique différent peut-il améliorer les performances ?
Revenons maintenant au graphique précédent du temps de résolution en fonction du nombre de degrés de liberté et discutons de 10 changements divers de matériel qui peuvent modifier le temps de résolution.
Utiliser un SSD au lieu d’un disque dur
Ceci est important dans la région où la mémoire virtuelle utilisée est nettement supérieure à la RAM physique. L’ordinateur utilisé pour générer la courbe illustrée précédemment est équipé d’un SSD, ce qui est courant dans la plupart des ordinateurs récents. Un disque dur (HDD) avec un plateau tournant et une tête de lecture ou d’écriture mobile, plutôt qu’une mémoire à semi-conducteurs, entraînerait des temps de résolution plus lents en comparaison. Lors de la résolution de modèles qui nécessitent moins de mémoire que la mémoire vive, ce choix a beaucoup moins d’effet. Il peut également être raisonnable d’avoir un disque dur de grande capacité en plus d’un SSD, lorsque le disque dur est principalement utilisé pour sauvegarder les données de simulation.
Ajouter de la mémoire
Cela améliorera la vitesse de résolution pour les modèles qui utilisent beaucoup plus de mémoire virtuelle que de mémoire physique, tant que la mémoire est ajoutée de manière équilibrée sur tous les canaux de mémoire. Par exemple, le processeur utilisé pour ces tests possède quatre canaux de mémoire et 32 Go de RAM, avec un DIMM de 8 Go par canal. Il est possible d’effectuer une amélioration en ajoutant quatre modules DIMM supplémentaires de 8 Go, un par canal (puisque cet ordinateur dispose d’un deuxième emplacement vide par canal de mémoire), ou en remplaçant les quatre modules DIMM de 8 Go par des modules DIMM de 16 Go. Dans tous les cas, il est important que les canaux soient tous remplis. Si, par exemple, un seul canal sur quatre est utilisé, alors la vitesse de résolution sera affectée de façon négative.
Passer à des modules DIMM plus rapides
En fonction du processeur, il peut être possible de passer à un module DIMM qui prend en charge des taux de transfert de données plus élevés. Il est important que tous les modules DIMM aient la même vitesse car un déséquilibre de la vitesse mémoire entre les modules DIMM conduira à la vitesse la plus basse communément supportée.
Passer à un processeur avec une fréquence d’horloge plus rapide
La fréquence d’horloge affecte tous les aspects du logiciel et une fréquence plus élevée est toujours un meilleur choix. D’un point de vue pratique, il n’est généralement pas possible d’améliorer la fréquence d’horloge tout en conservant le reste. Il est donc impossible d’isoler les améliorations et, dans la plupart des cas, il faudrait acheter un nouvel ordinateur. Toutefois, à mesure que les modèles deviennent plus volumineux en termes d’utilisation de la mémoire et que davantage de données doivent être transférées de la RAM, le goulot d’étranglement des performances tend à être la vitesse de transfert des données vers et depuis la mémoire RAM, plutôt que la vitesse du CPU.
Passer à un processeur avec plus de cœurs
Étant donné qu’il est difficile de passer à un plus grand nombre de cœurs tout en maintenant tous les autres facteurs constants, il n’est pas facile de déterminer les effets d’un plus grand nombre de cœurs. Dans la plupart des cas, lors de la résolution d’un seul modèle, il n’y a pas beaucoup d’avantages à utiliser plus de huit cœurs par job. Si le temps de résolution est dominé par le solveur linéaire direct, l’utilisation de plus de cœurs sera plus avantageuse. D’autre part, les très petits modèles peuvent être résolus plus rapidement sur un seul cœur, même si plusieurs cœurs sont disponibles. En d’autres termes, la parallélisation a un coût de calcul qui peut être important pour les petits modèles.
Séparément, de multiples cœurs sont également avantageux lors de l’exécution de plusieurs jobs en parallèle, comme lors de l’utilisation de la fonctionnalité Batch paramétrique de COMSOL Multiphysics®. Certains processeurs offrent désormais à la fois des cœurs de performance et des cœurs d’efficacité, ce qui introduit des compromis supplémentaires en matière de performance.
Passer à un processeur avec un cache plus important
Une mémoire cache plus importante est toujours préférable, mais la taille de la mémoire cache est proportionnelle au nombre de cœurs, de sorte que les processeurs dotés de la mémoire cache la plus élevée auront un nombre de cœurs élevé et seront relativement chers.
Passer à un ordinateur doté d’un processeur avec plus de canaux de mémoire
Il est possible d’acheter un ordinateur à processeur unique qui possède deux, quatre, six ou même huit canaux de mémoire. Le passage d’un nombre de canaux à l’autre représente également un passage d’une classe de processeurs à l’autre et il est très difficile de comparer les performances entre elles sur la base des seules spécifications matérielles. Plus de quatre canaux sont justifiés si vous résolvez régulièrement de très grands modèles ou plusieurs modèles en parallèle.
Passer à un ordinateur à deux processeurs
Les processeurs qui prennent en charge le fonctionnement en mode dual-socket disposent de six ou huit canaux de mémoire par processeur, pour un total de 12 ou 16 canaux. Ces systèmes disposent donc de 96 Go de RAM au minimum, ce qui les destine principalement à la résolution de modèles de grande taille ou à la résolution de nombreux modèles en parallèle.
Passer à un ordinateur à 4 CPU ou plus
Il s’agit d’une catégorie très limitée qui ne devrait être envisagée que pour les modèles nécessitant de très grandes quantités de mémoire RAM (au moins 768 Go). Avant d’envisager un tel système, contactez notre équipe Support pour obtenir des conseils personnalisés.
Passer à un cluster
Il existe des milliers de clusters existants, dont une fraction significative est déjà utilisée pour exécuter COMSOL®. L’écosystème du matériel de cluster disponible est si vaste — et change si rapidement — qu’il n’est pas possible d’émettre des affirmations sur les performances relatives. Il existe également un certain nombre de fournisseurs de services de calcul cloud qui peuvent rapidement vous permettre de faire tourner une ressource de calcul temporaire sur le matériel de votre choix afin que vous puissiez comparer les performances relatives sur un large éventail de matériel. En termes de résolution de modèles extrêmement volumineux, les clusters ont l’avantage de pouvoir utiliser des solveurs utilisant la décomposition de domaine. Bien entendu, les clusters sont également utiles pour résoudre des centaines, voire des milliers, de cas en parallèle au sein d’un balayage paramétrique sur cluster.
Note : En complément de tous ces facteurs, il y a aussi la génération et l’architecture du processeur à prendre en compte. Les processeurs sont mis à jour de manière significative presque chaque année et il y a plusieurs mises à jour mineures par an. Il est assez difficile de comparer les paramètres ci-dessus entre les différentes générations de processeurs, mais en général, les processeurs de nouvelle génération sont plus performants que les anciens.
Comment dois-je décider de l’ordinateur à acheter ?
Pour décider du type d’ordinateur à acheter, le processus commence par le choix d’un modèle, ou d’un ensemble de modèles, qui décrit le type d’analyse que vous souhaitez effectuer. Ensuite, vous effectuerez une étude de scalabilité pour identifier les besoins en mémoire, car votre simulation doit se développer. Bien sûr, vous devrez faire un peu de supposition et d’extrapolation, il est donc bon de surestimer la mémoire dont vous aurez besoin.
Une fois que vous avez une bonne idée de la quantité de mémoire dont vous aurez besoin, décidez entre les processeurs de dernière génération en termes de nombre de canaux de mémoire. C’est ici que vous disposez de la plus grande flexibilité et vous devez donc penser à la possibilité d’augmentation de la mémoire. Si vous avez sous-estimé les besoins en mémoire, vous devez pouvoir installer facilement plus de RAM. Par exemple, l’ordinateur utilisé pour générer les données précédentes dispose de 32 Go de RAM, installés sur un système à quatre canaux de mémoire avec un DIMM de 8 Go par canal, et il y a un emplacement disponible par canal, il serait donc facile de passer à 64 Go de RAM en achetant quatre autres DIMM de 8 Go.
Ensuite, en ce qui concerne le choix d’un processeur, assurez-vous que l’architecture du processeur prend en charge la vitesse de mémoire la plus rapide disponible et, au sein de cette architecture, choisissez la fréquence d’horloge la plus rapide. Il existe généralement un compromis entre la fréquence d’horloge et le nombre de cœurs. La taille du cache tend à augmenter avec le nombre de cœurs, mais le fait d’avoir plus de deux cœurs par canal de mémoire conduit généralement à des rendements décroissants en termes de performances par rapport au coût du matériel.
Gardez également à l’esprit quelques autres facteurs, tels que l’utilisation d’un SSD si vous prévoyez une utilisation importante de mémoire virtuelle. En ce qui concerne les cartes graphiques, la liste du matériel pris en charge se trouve ici et les cartes graphiques à mémoire et vitesse plus élevées offriront toujours de meilleures performances d’affichage. De plus, les ordinateurs sont souvent conçus pour certains marchés et à différents niveaux de prix, par exemple, des stations de travail plus chères ou des ordinateurs grand public plus économiques. Ces derniers peuvent parfois avoir de meilleures performances optimales, mais les systèmes de type station de travail peuvent être plus fiables, en particulier lorsqu’il s’agit de faire fonctionner de très grands modèles pendant plusieurs heures ou plusieurs jours d’affilée.
Qu’est-ce qui va encore améliorer les performances ?
À ce stade, vous avez peut-être envie d’acheter du nouveau matériel pour exécuter les calculs de vos modèles. Mais avant de le faire, réfléchissez à la valeur du modèle que vous construisez. Un modèle numérique de valeur est un modèle dont vous allez exécuter des milliers (ou plus !) de variations au cours de votre carrière. En optimisant les performances de ces modèles, vous gagnerez des semaines, voire des mois, et ce, quel que soit le matériel utilisé.
Division des modèles en catégories
Pour savoir comment exécuter les calculs de nos modèles le plus rapidement possible, quel que soit le matériel utilisé, nous pouvons diviser conceptuellement les modèles en trois catégories.
1. Stationnaire linéaire
Ces modèles comprennent les cas où les propriétés matériaux, les chargements et les conditions aux limites sont indépendantes de la solution. Les modèles résolus dans le domaine fréquentiel et les modèles de calcul de valeurs propres ou de fréquences propres peuvent également être classés dans cette catégorie. Pour ces cas, le temps de calcul est uniquement lié au nombre de degrés de liberté, de sorte que l’objectif doit toujours être de réduire le nombre de degrés de liberté autant que possible tout en obtenant la précision souhaitée.
2. Stationnaire non-linéaire
Ces modèles comprennent tous les cas où des termes non linéaires apparaissent dans les équations, comme dans les équations de Navier–Stokes, ou lorsque les propriétés matériaux, les chargements ou les conditions aux limites sont fonction de la solution. La solution de tels cas est obtenue en résolvant de manière répétée un problème linéarisé. Dans ce cas, le temps de calcul est une combinaison du coût de l’itération linéarisée et du taux de convergence du problème non linéaire. La réduction du coût de calcul implique non seulement de maintenir le nombre de degrés de liberté aussi bas que possible tout en obtenant la précision souhaitée, mais aussi d’améliorer le taux de convergence du problème non linéaire. En d’autres termes, il s’agit de réduire le nombre d’étapes nécessaires pour parvenir à la solution. Tandis que la réduction du nombre de degrés de liberté affecte à la fois le temps de résolution et la mémoire, le taux de convergence affecte presque uniquement le temps de résolution.
3. Transitoire
Ces modèles calculent une solution dans le temps en résolvant une séquence d’approximations stationnaires à un nombre discret de pas de temps, et peuvent inclure ou non des termes non-linéaires. La préoccupation supplémentaire ici est de réduire le nombre de pas de temps discrets, ainsi que le nombre de pas linéarisés par pas de temps, tout en ayant un maillage suffisamment fin pour résoudre les champs variant dans le temps.
Techniques de modélisation utiles
Bien que chaque problème soit unique, il existe des techniques très communes que tous les analystes devraient avoir dans leur boîte à outils, notamment :
- Lorsque vous travaillez avec des fichiers CAO importés, utiliser les fonctionnalités de Simplification et réparation et d’ Opérations virtuelles pour approximer les données CAO afin de fournir une géométrie plus simple, ou utiliser la symétrie pour réduire la taille du modèle CAO.
- Lorsqu’il s’agit de géométries relativement fines ou petites, utiliser une géométrie simplifiée ainsi que des interfaces physiques éventuellement différentes, comme dans cet exemple de coques et poutres pour la modélisation de structures. Ou, faire appel à des conditions aux limites spécifiques au lieu de modéliser explicitement la géométrie des domaines de faible épaisseur.
- Faire appel à des maillages extrudés ainsi qu’à des maillages non-conformes dans la mesure du possible, et en connaissant parfaitement la construction manuelle de maillages.
- Pour les problèmes stationnaires non-linéaires, comprendre les différentes façons d’améliorer la convergence.
Il ne s’agit là, bien entendu, que des grandes lignes. Il existe d’innombrables techniques de modélisation spécialisées qui peuvent n’être applicables que de manière très limitée, mais qui peuvent rendre vos modèles beaucoup plus efficaces. Apprendre ces techniques, et savoir exactement quand et comment les appliquer, est l’art et le métier du modélisateur numérique expérimenté.
Remarques finales
Nous avons commencé ici par poser une question apparemment simple et, en y répondant, nous avons abordé un large éventail de sujets. Je terminerai cet article en montant sur ma tribune et en adoptant une position un peu controversée. À mon avis, essayer de résoudre des modèles de plus grande taille sur des ordinateurs plus rapides est une méthode de calcul de dernier recours. Il est de loin préférable de passer son temps à chercher comment rendre ses modèles plus petits et plus rapides, quel que soit le matériel utilisé. Il arrivera un jour où vous devrez investir dans du meilleur matériel, et lorsque vous en arriverez là, vous voudrez savoir exactement pourquoi vous devez passer au niveau supérieur. Nous espérons que vous disposez maintenant d’un cadre pour comprendre comment aborder ce processus.
Intel et Xeon sont des marques commerciales d’Intel Corporation ou de ses filiales.
Microsoft et Windows sont des marques déposées de Microsoft Corporation aux États-Unis et/ou dans d’autres pays.



Commentaires (0)