
Le plissement est un sujet de recherche qui concerne aussi bien l’ingénierie spatiale, avec les antennes gonflables, que la bio-ingénierie, avec le phénomène bien connu du plissement de la peau. Quel que soit le domaine dans lequel ils travaillent, les ingénieurs et les chercheurs qui s’occupent de structures minces connaissent le mécanisme sous-jacent du plissement : un manque de rigidité ou une rigidité réduite lorsqu’une structure mince est soumise à des contraintes de compression. Dans cet article de blog, nous verrons comment modéliser le plissement à l’aide du logiciel COMSOL Multiphysics®.
Introduction
Dans les simulations mécaniques, les structures minces sont généralement modélisées à l’aide d’éléments coques ou membranes. Les éléments coques prennent en compte la rigidité en flexion de la structure, ce qui n’est pas le cas des membranes. Cette différence fondamentale définit la manière dont ces deux types d’éléments gèrent la modélisation du plissement. Lorsque la rigidité en flexion est prise en compte, comme dans le cas des modèles de coque, le plissement est observé pour une contrainte de compression critique caractérisée par la rigidité en flexion. En revanche, si la rigidité en flexion n’est pas prise en compte, comme dans le cas des modèles de membranes, le plissement est observé dès l’apparition des contraintes de compression.
Dans les deux cas, le plissement est considéré comme étant une instabilité, également connu sous le nom de flambage local. Lorsqu’on modélise le plissement à l’aide d’éléments coques, il est nécessaire de mener une analyse post-flambement. Il est à noter que la discrétisation du maillage et toute imperfection géométrique peuvent avoir un impact significatif sur les résultats finaux. Les modèles de coques ont l’avantage de fournir des informations détaillées sur les caractéristiques du plissement, telles que les longueurs d’onde et les amplitudes. Cependant, dans de nombreux scénarios de modélisation, ces caractéristiques ne sont pas particulièrement pertinentes ; l’objectif principal est plutôt d’éviter le plissement dans la zone problématique. Dans ce cas, la modélisation des plis à l’aide d’éléments de membrane peut s’avérer avantageuse, car cette approche ne requiert que peu de ressources de calcul et offre une meilleure stabilité numérique.
Dans la suite de cet article, nous examinons ces deux approches de modélisation l’une après l’autre. Dans COMSOL Multiphysics®, les éléments de coque et de membrane sont modélisés à l’aide des interfaces Coque et Membrane, respectivement.

Un autre exemple familier de plissement : celui d’une voile. Photo de Karla Car sur Unsplash. L’oeuvre originale a été modifiée.
Modéliser avec l’interface Membrane
Une structure mince modélisée avec l’interface Membrane peut être dans l’un des trois états suivants lorsqu’elle est déformée :
- Tendue — lorsque les deux contraintes principales dans le plan sont positives
- Lâche — lorsque les deux contraintes principales dans le plan sont négatives
- Plissée — lorsque l’une des contraintes principales dans le plan est négative
La théorie classique des membranes utilise une formulation basée sur l’énergie de déformation totale, tenant compte des contraintes de compression dans les régions plissées, ce qui conduit à des solutions d’équilibre instables. Pour prévenir cette instabilité, la théorie modifiée des membranes (basée sur la théorie des champs de tension) a été développée. La théorie modifiée des membranes renvoie un état de contrainte uniaxiale dans la région plissée et un état de contrainte nulle dans la région lâche, ce qui permet d’éviter l’instabilité de l’équilibre. La théorie modifiée des membranes peut être formulée selon deux approches principales : en modifiant le tenseur des déformations ou la loi de comportement.
Modification du tenseur des déformations
Pour comprendre la cinématique du plissement, examinons le schéma suivante :
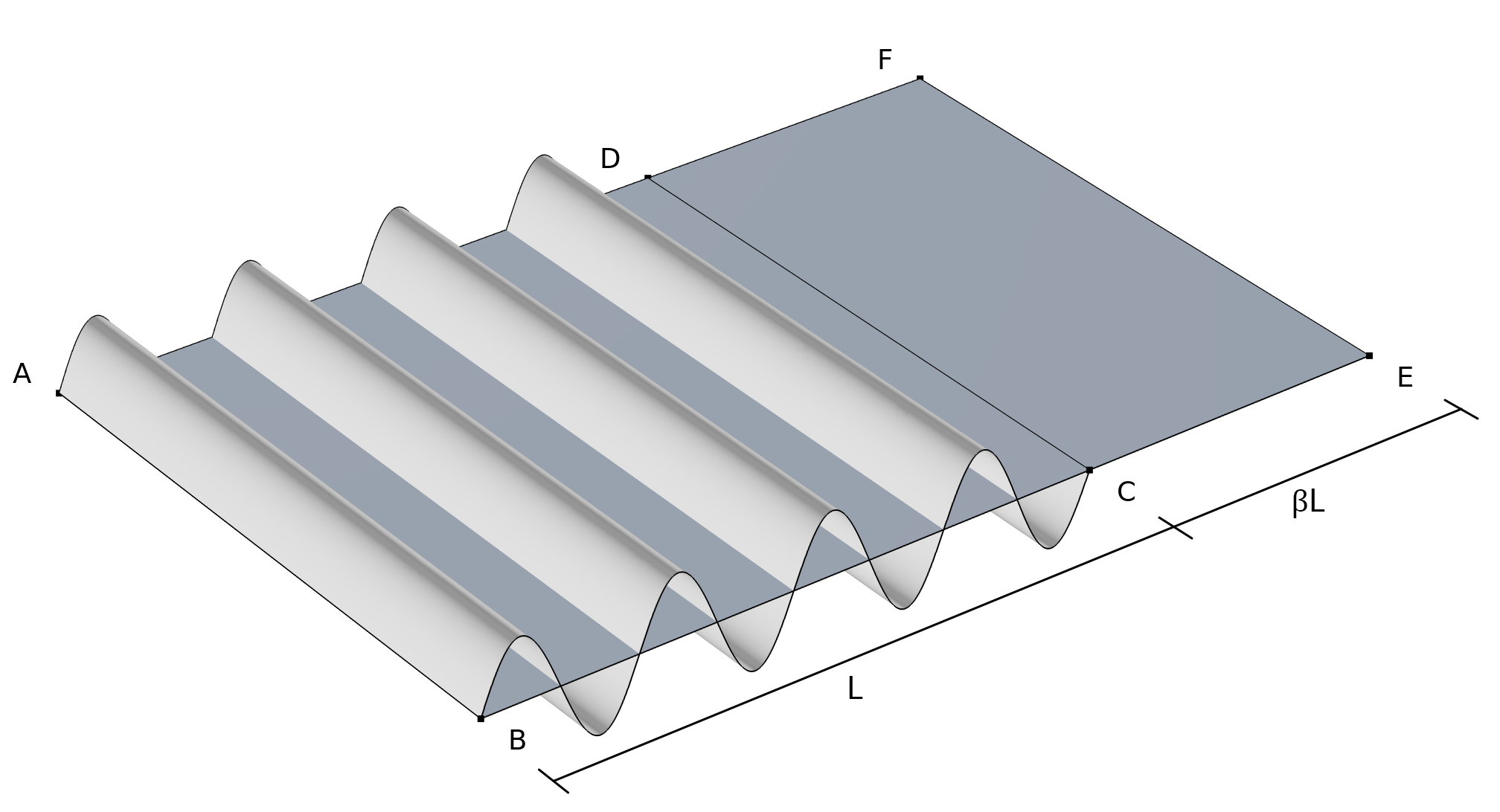
Cinématique du plissement. La surface courbe ABCD représente la configuration plissée, la surface plane ABCD représente la configuration moyenne et la surface plane ABEF représente la configuration allongée.
Pour la membrane plissée, la figure ci-dessus illustre trois descriptions cinématiques différentes:
- Le tenseur des déformations \widetilde{\bf{F}} relie la configuration de référence à une véritable configuration plissée (surface courbe ABCD).
- Ne permet pas de déterminer le champ de déformation dans la membrane plissée
- Le tenseur des déformations \bf{F} relie la configuration de référence à une configuration moyenne (surface plane ABCD), dont la surface est plus petite que la surface plissée réelle.
- Ne permet pas de déterminer le champ de déformation dans la membrane plissée
- Le tenseur des déformations \bar{\bf{F}} relie la configuration de référence à une configuration allongée fictive (surface plane ABEF), dont la surface correspond à la surface plissée réelle.
- Permet de déterminer le champ de déformation dans la membrane plissée
En supposant que le plissement se produit dans la direction \bf{n}_2 et que \bf{n}_1 est la direction de la tension uniaxiale, le tenseur des déformations modifié \bar{\bf{F}} peut s’écrire
où \beta est un paramètre d’allongement/de plissement (Ref. 1). Le symbole \otimes désigne le produit tensoriel (dyadique) de deux vecteurs, qui engendre un tenseur. \beta=0 représente un état tendu. Selon la condition d’orthogonalité et la théorie des surfaces de tension,
où \bf{\sigma} est la contrainte de Cauchy, écrite à partir du second tenseur des contraintes de Piola–Kirchhoff comme suit
En supposant que la configuration moyenne est connue (\bf{F}), les seules inconnues sont \bf{n}_2 et \beta.
Formulons ces équations dans la configuration de référence, ce qui en soit est plus pratique, puisque la cinématique et les propriétés matériaux de la membrane sont exprimés dans la configuration de référence. Nous supposons que \bf{h} est un vecteur dans la configuration de référence correspondant au vecteur \bf{n}_2. Ainsi, le tenseur fictif des déformations de Green–Lagrange \bar{\bf{E}} s’écrit
où \bf{C} est le tenseur moyen de Cauchy-Green à droite, \bf{N}_2 est le vecteur unitaire dans la configuration de référence, et \beta^* est le nouveau paramètre de plissement.
La surface de la membrane est représentée par un système de coordonnées comportant deux vecteurs unitaires orthogonaux dans le plan, \bf{e}_1 et \bf{e}_2. \bf{N}_1 et \bf{N}_2 s’écrivent en fonction de l’angle comme suit
Les deux équations non linéaires couplées à résoudre pour deux inconnues, \alpha et \beta^*, sont
Ces deux équations algébriques non linéaires peuvent être résolues par la méthode de Newton–Raphson :
f_{1,\alpha} & f_{1,\beta^*}\\
f_{2,\alpha} & f_{2,\beta^*}
\end{pmatrix} \begin{pmatrix}
\Delta \alpha\\
\Delta \beta^*
\end{pmatrix} = \begin{pmatrix}
-f_1\\
-f_2
\end{pmatrix}.
Ici, \alpha et \beta^* sont résolus par la méthode de Newton–Raphson au niveau local en chaque point de Gauss et pour chaque itération au niveau global.
La fonctionnalité Plissement
L’approche fondée sur la modification du tenseur des déformations est mise en oeuvre dans le sous-noeud intégré Plissement, qui peut être ajouté aux noeuds Matériau élastique linéaire et Matériau hyperélastique de l’interface Membrane. Le sous-noeud Plissement propose trois options différentes pour définir le critère d’arrêt de la méthode locale de Newton–Raphson, avec la possibilité d’ajuster les tolérances.

Le sous-noeud Plissement ajouté à la loi de comportement Matériau élastique linéaire .
Plusieurs modèles de la Bibliothèques d’Applications montrent comment modéliser le plissement en utilisant la fonctionnalité prédéfinie de l’interface Membrane. Le modèle suivant est simple, et peut être aisément vérifié analytiquement: Uniaxial Stretching of a Rectangular Membrane. Dans cet exemple, les résultats numériques sont comparés aux résultats analytiques, comme illustré ci-dessous :
La région plissée d’une membrane rectangulaire est représentée en rouge foncé. Dans la figure de gauche, un matériau isotrope est utilisé, et dans la figure de droite, un matériau orthotrope. Dans les deux figures, les résultats analytiques sont comparés aux résultats de la simulation.
Le modèle Inflation of a Square Airbag est plus concret et donc plus sophistiqué. Le modèle montre l’apparition de plis dans un airbag carré au moment de son gonflage. Ce modèle utilise un matériau élastique linéaire, tandis qu’un modèle similaire, Inflation of a Square Hyperelastic Airbag, utilise un matériau hyperélastique.
Airbag carré modélisé avec un matériau élastique linéaire. La région plissée est représentée en rouge foncé.
Un autre exemple utilisant la fonctionnalité intégrée de l’interface Membrane pour analyser le plissement est le modèle Torsion of a Circular Membrane, dans lequel un couple est appliqué sur le bord intérieur d’un anneau pour produire des plis. Dans cet exemple, on examine l’impact de différents maillages et de différentes discrétisations sur les plis.
Modification de la loi de comportement
Comme décrit ci-dessus, le sous-noeud Plissement de COMSOL Multiphysics® utilise la formulation du tenseur des déformations modifié. Cependant, la flexibilité du logiciel permet également de modéliser les plissements selon la seconde approche, qui consiste à modifier la loi de comportement.
Dans cette seconde formulation, la loi de comportement est modifiée pour tenir compte de la région plissée. L’énergie de déformation utilisée dans la région plissée est appelée énergié de déformation relaxée, tandis que l’énergie de déformation dans la région tendue est appelée énergie de déformation totale. Cette approche est applicable à toutes les lois de comportement hyperélastiques isotropes, mais par souci de simplicité, nous considérons ici un modèle Néo-hookéen incompressible. La densité d’énergie de déformation totale exprimée en fonction des élongations principales \lambda_1 et \lambda_2 peut être écrite sous la forme suivante :
La contrainte principale de Cauchy \sigma est donnée par
La contrainte principale de Cauchy dans chaque direction est donnée par
Supposons que l’étirement ait lieu suivant la première direction principale et que le plissement survienne selon la deuxième direction principale. Dans ce cas, l’équation suivante doit être vérifiée dans la région plissée :
Cette équation définit un état de contrainte uniaxiale dans la région plissée. La contrainte dans la direction du plissement devenant alors nulle, on en déduit la condition en fonction des élongations principales:
Par conséquent, la région de plissement est définie par l’inégalité suivante : \lambda_2 \sqrt{\lambda_1} < 1. En insérant la condition de plissement écrite à partir des élongations principales dans l’énergie de déformation totale, on obtient l’énergie de déformation relaxée pour la loi de comportement Néo-hookéenne :
L’énergie de déformation relaxée ne dépend pas de l’allongement dans la direction du plissement ; cela signifie que la contrainte de Cauchy dans cette direction devient automatiquement nulle.
En utilisant la condition de plissement et les densités d’énergie ci-dessus, la densité d’énergie de déformation pour les régions tendues et plissées s’écrit comme suit
On peut montrer que, pour les membranes isotropes, les deux formulations, utilisant le tenseur des déformations modifié ou la loi de comportement modifiée, sont équivalentes. (Voir Ref. 1 pour plus de détails). Cependant, l’approche basée sur les la loi de comportement modifiée ne s’applique qu’aux membranes isotropes, tandis que l’approche utilisant le tenseur des déformations modifié est plus générale et s’applique également aux membranes anisotropes.
Comparaison des formulations dans COMSOL Multiphysics®
Dans le tutoriel Wrinkling of Cylindrical Membranes with Varying Thickness, les résultats obtenus avec les deux formulations sont comparés et se révèlent être identiques. Dans le modèle, la membrane cylindrique est d’abord étirée axialement, puis gonflée sous la pression de l’eau. Pendant le gonflage, les extrémités sont maintenues fixes.
Dans COMSOL Multiphysics®, la formulation utilisant une modification de la loi de comportement peut être mise en oeuvre en sélectionnant l’option Défini par l’utilisateur de la loi de comportement Matériau hyperélastique. Notez que dans ce tutoriel, l’énergie de déformation du modèle Néo-hookéen a été spécifiquement formulée pour une membrane isotrope incompressible. Il convient donc de ne pas utiliser la formulation incompressible prédéfinie, car cette-ci ajoute des termes supplémentaires qui pourraient être source de conflit. Vous pouvez à la place utiliser l’option Compressible dans le matériau hyperélastique défini par l’utilisateur, qui utilise la densité d’énergie de déformation telle qu’elle est écrite.
 Un sous-noeud Plissement (qui utilise la formulation modifiée du tenseur de déformation) et un modèle de matériau hyperélastique défini par l’utilisateur (qui utilise la formulation modifiée de la loi de comportement).
Un sous-noeud Plissement (qui utilise la formulation modifiée du tenseur de déformation) et un modèle de matériau hyperélastique défini par l’utilisateur (qui utilise la formulation modifiée de la loi de comportement).
Les figures ci-dessous montrent la région plissée d’une membrane cylindrique à différentes hauteurs d’eau selon les deux approches de modélisation. Les résultats présentés montrent que les deux approches sont sensiblement équivalentes et produisent les mêmes résultats.
La région plissée d’une membrane cylindrique est représentée en rouge foncé. Les résultats sont obtenus avec l’approche du tenseur de déformation modifié (à gauche) et l’approche de la loi de comportement modifiée (à droite). Les annotations indiquent les différentes hauteurs de fluide dans la membrane, qui mesure 80 mm de haut pour un rayon de 10 mm.
Modélisation avec l’interface Coque
Le traitement du plissement avec l’interface Coque repose sur l’analyse des bifurcations. Le plissement est considéré comme un phénomène de flambage local dû aux contraintes de compression ; par conséquent, une analyse post-flambement est nécessaire pour le modéliser. L’avantage de ce type d’analyse est qu’elle permet de déterminer les longueurs d’onde et les amplitudes du plissement. La première étape consiste en une analyse des valeurs propres de la structure précontrainte, qui permet d’identifier les modes de flambement potentiels. Ensuite, les quelques modes de flambement sélectionnés sont mis à l’échelle et utilisés comme imperfection géométrique pour l’analyse post-flambement.
Dans le tutoriel Uniaxial Stretching of a Rectangular Sheet, l’apparition de plis dans une tôle mince rectangulaire est étudiée à l’aide de l’analyse post-flambement des coques. La capture d’écran suivante montre l’arborescence du Constructeur de modèles avec les noeuds requis pour mener à bien cette analyse.
 Le noeud Imperfection en flambage et les études nécessaires pour le modèle Uniaxial Stretching of a Rectangular Sheet.
Le noeud Imperfection en flambage et les études nécessaires pour le modèle Uniaxial Stretching of a Rectangular Sheet.
La première étape de ce tutoriel consiste à identifier les régions potentiellement plissées à l’aide d’une analyse statique. Dans cette étape, la coque est soumise à un allongement uniaxial. L’objectif est de trouver la région dans laquelle la deuxième contrainte principale devient compressive. Ensuite, on effectue une analyse de flambage précontraint en utilisant une étape Stationnaire suivie d’une étape Flambage linéaire.
Pour l’analyse post-flambement, on peut utiliser la fonctionnalité Imperfection en flambage, comme illustré dans la capture d’écran ci-dessus. Ce noeud permet de spécifier le nombre souhaité de modes de flambage, ainsi que leurs facteurs d’échelle respectifs. Ces modes mis à l’échelle sont ensuite combinés et appliqués en tant qu’imperfections géométriques pour l’analyse post-flambement. Depuis ce noeud, il est également possible de générer une étude paramétrique de flambage non linéaire.
L’animation ci-dessous montre le plissement d’une feuille rectangulaire sous l’effet d’une déformation uniaxiale croissante, tandis que la deuxième figure montre l’amplitude des plis le long de la ligne centrale dans la direction du plissement. Dans un premier temps, lorsque la déformation de la feuille rectangulaire augmente, des plis commencent à se former. L’amplitude de ces plis croît à mesure que la déformation augmente jusqu’à atteindre une valeur critique, après quoi cette amplitude commence à décroître. Au-delà d’une certaine valeur de déformation, l’amplitude des plis devient très faible.
Plissement dans une analyse post-flambement. Le système de couleurs représente l’amplitude des plis, le bleu indiquant les valeurs négatives, le rouge les valeurs positives et le vert le déplacement nul.
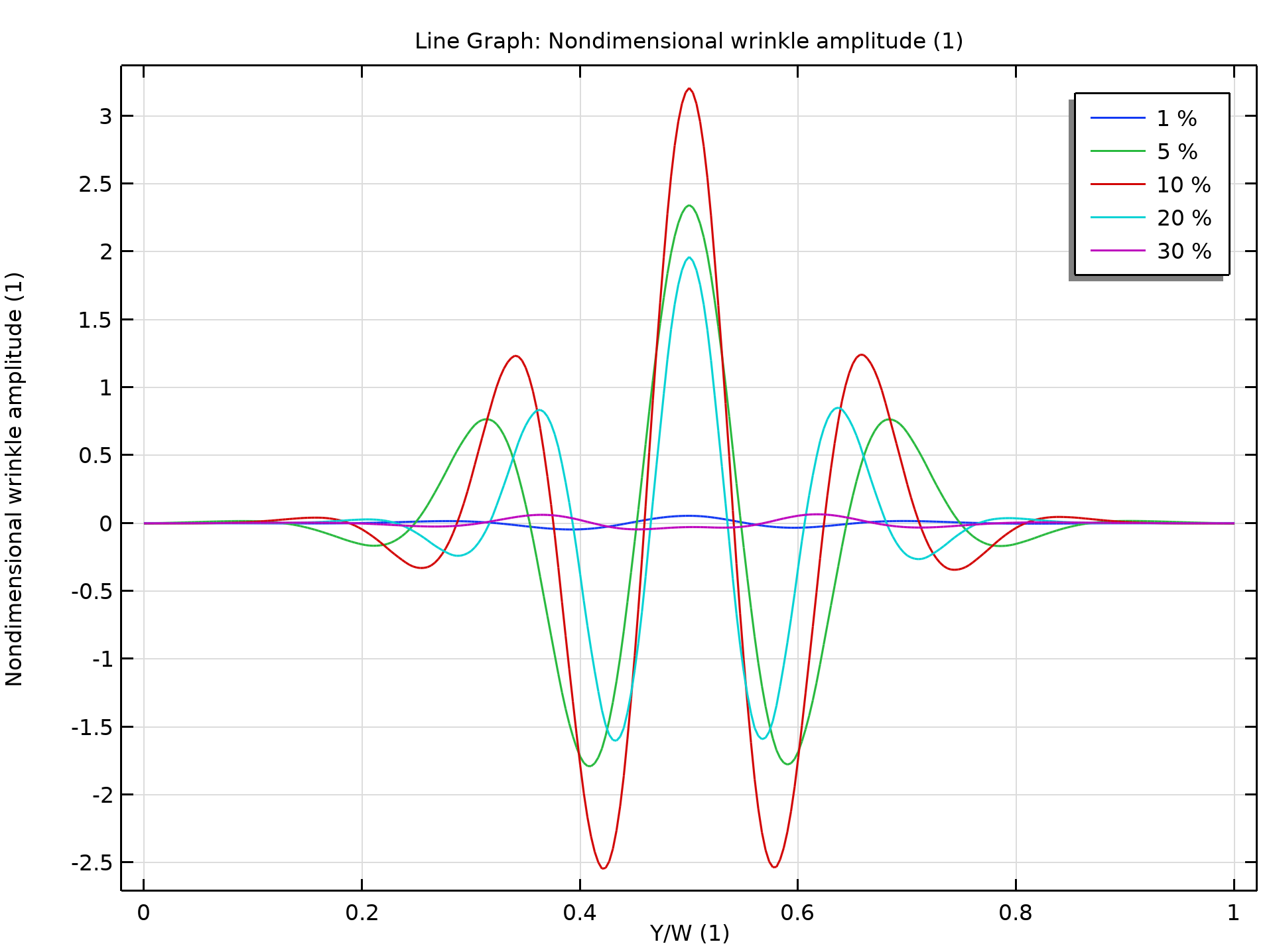
Amplitude des plis dans une analyse post-flambement.
Conclusions
Nous avons montré que le plissement peut être modélisé dans COMSOL Multiphysics® à l’aide des interfaces Membrane et Coque. L’analyse membranaire des plis peut être abordée en modifiant le tenseur de déformation ou la loi de comportement. Cette analyse est rapide et numériquement efficace, et permet d’identifier de manière correcte les régions de plissement et la distribution des contraintes. Cependant, elle ne fournit pas d’informations sur les amplitudes et les longueurs d’onde des plis. L’analyse membranaire des plis peut être abordée en modifiant le tenseur de déformation ou la loi de comportement. Cette analyse est rapide et numériquement efficace, et permet d’identifier de manière correcte les régions de plissement et la distribution des contraintes. Cependant, elle ne fournit pas d’informations sur les amplitudes et les longueurs d’onde des plis. Par ailleurs, l’analyse des plis à l’aide des coques est longue, exigeante sur le plan numérique et sensible aux imperfections géométriques. Elle fournit toutefois des données précieuses sur les amplitudes et les longueurs d’onde des plis, en plus de prédire correctement la distribution des contraintes et les régions plissées.
Les deux types d’analyse ayant leurs avantages et inconvénients respectifs, les ingénieurs peuvent choisir l’une ou l’autre en fonction des exigences spécifiques de la modélisation.
Références
- A. Patil, Inflation and Instabilities of Hyperelastic Membranes, PhD thesis, Royal Institute of Technology (KTH), Stockholm, 2016.
- H. Schoop et al., “Wrinkling of nonlinear membranes,” Computational Mechanics, vol. 29, pp. 68–74, 2002; https://doi.org/10.1007/s00466-002-0326-y



Commentaires (0)