Il est assez courant d’utiliser une lumière laser focalisée pour chauffer rapidement des matériaux à diverses fins, notamment dans l’industrie des semi-conducteurs. Ici, nous nous intéresserons à un faisceau laser à profil gaussien avec une intensité pulsée périodique, chauffant deux matériaux semi-transparents différents déposés sur un substrat de silicium. Pour modéliser cela, nous allons résoudre un problème de simulation multiphysique faisant intervenir le champ de température et la loi de Beer–Lambert. Explorons davantage ce modèle et voyons comment le mettre en oeuvre…
Un faisceau laser à profil gaussien appliqué sur un wafer de silicium
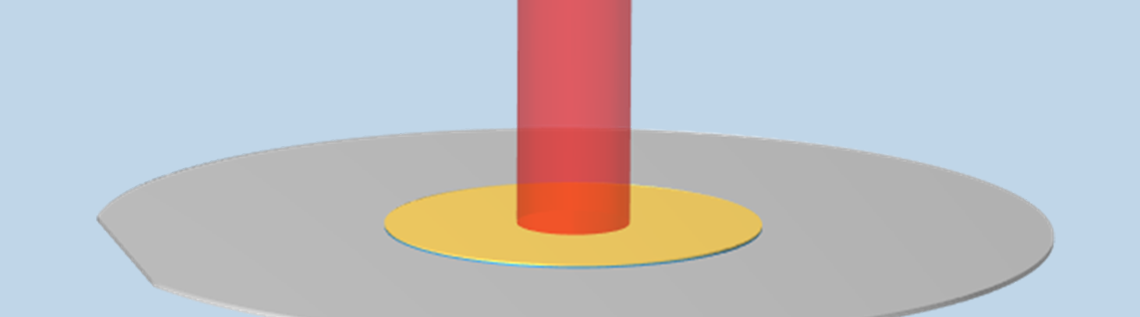
Nous utiliserons l’exemple d’un wafer de silicium de deux pouces de diamètre (illustré ci-dessous) comportant deux matériaux différents en son centre, chacun d’une épaisseur de 100 μm et d’un rayon de 1 cm. Le wafer est exposé par le haut à une source de chaleur laser à profil gaussien pulsée à haute fréquence. Ces matériaux sont tous deux semi-transparents à la longueur d’onde du laser de 700 nm, mais sont opaques aux rayonnements infrarouges de plus grande longueur d’onde. Le substrat de silicium est dopé et fortement absorbant à toutes les longueurs d’onde.
![]()
Un laser pulsé est appliqué à deux couches de matériau semi-transparents sur un wafer opaque.
Étant donné que tous les matériaux ont des frontières planes et normales au faisceau incident, toute la lumière incidente se propage dans une direction uniforme parallèle au faisceau incident. Il y aura de la réflexion à l’interface entre les matériaux, mais pas de réfraction ni de diffraction. L’épaisseur des deux couches est beaucoup plus grande que la longueur d’onde, nous pouvons donc supposer que la longueur de cohérence est beaucoup plus petite que l’épaisseur de la couche. Nous pouvons résoudre ce problème en utilisant la loi de Beer–Lambert, décrivant l’atténuation de la lumière au sein d’un milieu semi-transparent. Cette équation est résolue par l’interface Faisceau radiatif en milieu absorbant du logiciel COMSOL Multiphysics®. Cependant, en raison du phénomène de réflexion, il y a quelques subtilités que nous allons devoir minutieusement examiner.
Comprendre les phénomènes physiques et préparer le modèle
Etant donné que les couches déposées sont circulaires et que le laser est appliqué au centre, nous pouvons négliger le méplat du wafer et considérer le modèle comme étant parfaitement axisymétrique. Cela nous permet de réduire le modèle dans un plan de modélisation 2D-axisymétrique. Dans ce plan, nous dessinons simplement trois rectangles représentant le wafer et les deux couches, et leur assignons des propriétés matériaux différentes. La géométrie et les matériaux étant ainsi définis, nous pouvons nous concentrer sur les aspects physiques.
Commençons par suivre la propagation du faisceau dans le vide, depuis la source laser au-dessus du wafer vers le bas le long de l’axez. Nous supposerons avoir à notre disposition un laser de 40 W et de longueur d’onde 700 nm, et que le faisceau possède un profil gaussien d’écart type 1.5 mm. Le laser est allumé durant 75 ms et éteint durant 25 ms, correspondant à un chauffage pulsé de période 100 ms avec un rapport cyclique de 75 pour cent. Ce type de chargement en créneaux est implémenté via l’interface Evènements, qui introduit une variable d’Etat discret, ONOFF, prenant pour valeur soit 0 soit 1 au cours du temps.
Nous ne modéliserons pas explicitement la source laser ni la propagation du faisceau dans le vide, mais simplement l’interaction de la lumière avec les matériaux. A la frontière de la couche supérieure, le matériau possède un indice de réfraction de n_{top}=2.4, et il y aura de la réflexion en raison de la différence entre les indices de réfraction, tel que décrit par les équations de Fresnel:
Bien que les équations soient valides pour des indices de réfraction complexes, il est raisonnable de ne considérer que la partie réelle dans nos évaluations, la partie imaginaire étant relativement petite. En faisant en outre l’hypothèse qu’il n’y a pas d’absorption à l’interface (tel qu’il résulterait d’un fin revêtement de matériau absorbant), la transmittance est donnée par T=1-R. Cela complète les informations dont nous avons besoin pour paramétrer la fonctionnalité Intensité incidente de l’interface Faisceau radiatif en milieu absorbant, tel qu’illustré dans la capture d’écran ci-dessous.
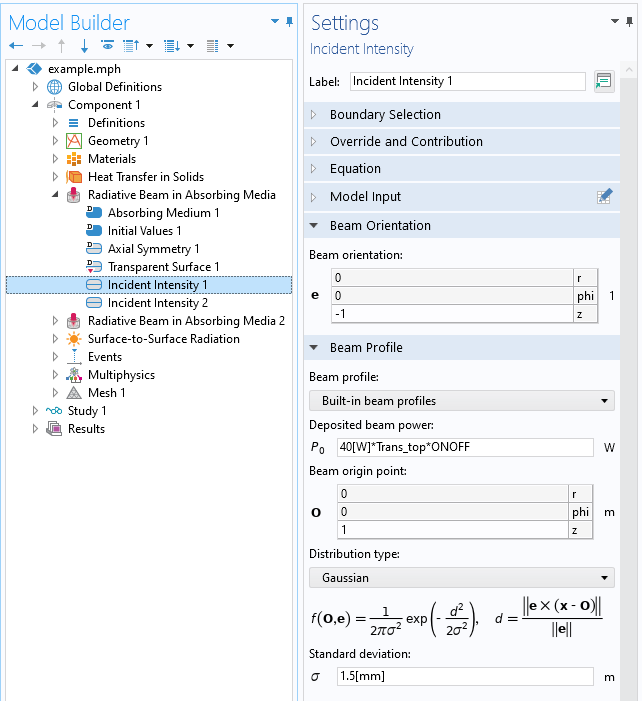
La fenêtre de réglages de la fonctionnalité Intensité incidente .
A mesure que le faisceau traverse la première couche de matériau, son intensité décroît proportionnellement au coefficient d’absorption, \kappa, qui est déterminé par l’équation:
avec k la partie imaginaire de l’indice de réfraction, et \lambda_0 la longueur d’onde du laser dans le vide. Le coefficient d’absorption peut dépendre de la température, mais nous utiliserons un coefficient constant dans un premier temps. A partir de la répartition de l’intensité du faisceau sur la frontière supérieure, l’intensité du faisceau à l’intérieur du domaine peut être calculée.
A l’interface diélectrique entre les couches supérieure et inférieure de matériau, il y aura à nouveau des phénomènes de réflexion et de transmission décrits par les équations de Fresnel. La composante réfléchie du faisceau est prise en compte par l’interface Faisceau radiatif en milieu absorbant existante, en ajoutant simplement un second noeud Intensité incidente. Il est possible d’ajouter autant de noeuds Intensité incidente que nécessaire; chacun introduisant une variable supplémentaire à résoudre, variables nommées respectivement rbam.I1, rbam.I2, …, et ainsi de suite. Dans ce second noeud Intensité incidente, nous pouvons renseigner un profil de faisceau défini par l’utilisateur à partir de l’intensité du premier faisceau et du coefficient de réflexion de Fresnel. En modifiant le signe de l’orientation du faisceau, la réflexion partielle de la lumière à l’interface est intégralement prise en compte, tel qu’illustré sur la capture d’écran ci-dessous. En théorie, une réflexion de ce faisceau aura lieu à la frontière supérieure, mais cette seconde réflexion est suffisamment faible pour que nous puissions la négliger.
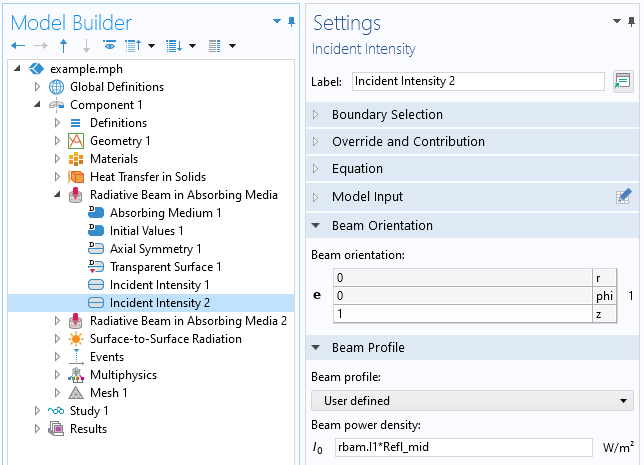
Capture d’écran du second noeud Intensité incidente, tenant compte de la réflexion à l’interface diélectrique.
Maintenant, nous allons suivre la propagation du faisceau à travers l’interface diélectrique jusqu’à la seconde couche de matériau semi-transparent. Etant donné qu’il y a une modification de l’intensité lumineuse à travers la frontière, nous devons ajouter une seconde interface Faisceau radiatif en milieu absorbant et définir l’intensité incidente à partir de la transmittance de Fresnel et du premier faisceau de l’interface Faisceau radiatif en milieu absorbant initiale.
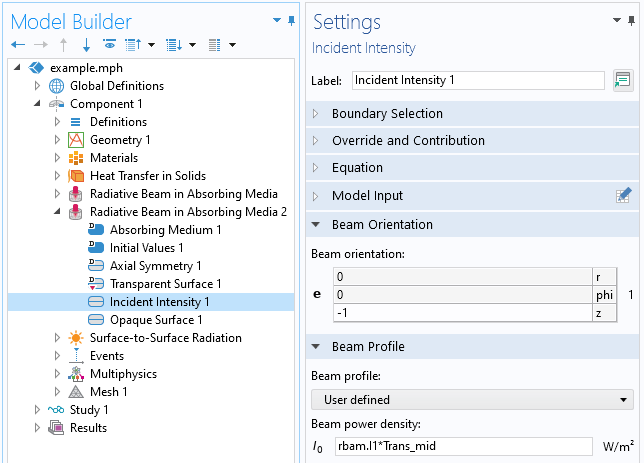
Capture d’écran du noeud Intensité incidente du faisceau de la seconde interface Faisceau radiatif en milieu absorbant, utilisée pour l’intensité du domaine inférieur.
Pour finir, intéressons-nous à ce qu’il se passe lorsque le faisceau atteint la frontière inférieure de la seconde couche, et frappe le substrat de silicium. Nous ferons l’hypothèse que le wafer de silicium est dopé de telle sorte qu’il est hautement absorbant et non réfléchissant. Puisque toute lumière atteignant cette frontière sera absorbée sur une distance relativement courte, nous pouvons considérer que la lumière est absorbée directement au niveau de la frontière. Dans cette situation, la condition aux limites Surface opaque Surface déposera l’intégralité de l’énergie sur la frontière sélectionnée, ce qui complète la modélisation de la propagation du faisceau laser à travers la structure. Avec cette combinaison de fonctionnalités, nous avons modélisé la propagation du faisceau laser incident à travers notre modèle. Nous pouvons désormais porter notre attention sur les aspects thermiques.
Modéliser l’évolution de la température au cours du temps
A l’instant initial, le wafer est à une température uniforme de 300 K. Il y a un transfert thermique par conduction à travers l’ensemble des domaines, et nous supposerons qu’il n’y a aucune résistance thermique significative aux interfaces entre les matériaux, en d’autres termes, qu’il n’y a aucun saut de température à travers les interfaces et que le flux est continu. Cette situation est l’hypothèse par défaut du logiciel, mais si nous souhaitions la remplacer, nous pourrions utiliser les fonctionnalités Couche mince ou Contact thermique.
A 100 μm, les couches sont suffisamment épaisses pour que la Loi de Fourier pour le transfert thermique soit applicable, bien qu’il soit intéressant de mentionner que le transfert thermique à l’échelle nanométrique est un domaine actif de recherche, notamment au sein de la communauté des utilisateurs COMSOL; voir par exemple notre article de blog rédigé par un contributeur invité “Hydrodynamic Thermal Transport in the Kinetic-Collective Model”.
En ce qui concerne les conditions aux limites de la thermique, nous supposerons que le wafer repose sur un support parfaitement isolé au sein d’une enceinte à très basse pression. Cela implique qu’il n’y aura aucun refroidissement par conduction ou par convection, mais il y aura en revanche transfert thermique par rayonnement vers les parois de l’enceinte que nous supposerons maintenues à 300 K. Nous ferons de plus l’hypothèse que la température du wafer n’augmentera que de quelques centaines de degrés Kelvin, et que le rayonnement sera émis sur une plage de longueurs d’onde plus longues que le laser incident. Par conséquent, nous pouvons, conceptuellement parlant, utiliser un modèle à deux bandes pour le rayonnement thermique. Le rayonnement incident du laser est intégralement modélisé par les interfaces Faisceau radiatif en milieu absorbant. Le rayonnement émis sur la plage de plus grandes longueurs d’onde (conséquence de l’élévation de température du wafer par rapport aux parois de l’enceinte) peut être modélisé via une interface Rayonnement de surface à surface simple bande, couplée à l’interface Transfert de chaleur dans des solides. L’interface Rayonnement de surface à surface calcule les facteurs de vue entre toutes les surfaces et vers l’espace ambiant.
Il est intéressant de mentionner que, dans ce cas précis, le rayonnement de surface à surface n’est présent qu’au voisinage de l’angle entrant à la jonction entre les couches et le wafer; le reste ayant un facteur de vue unitaire vers l’ambiant. Si nous souhaitions faire une légère modification, nous pourrions omettre l’interface Rayonnement de surface à surface et utiliser à la place une condition aux limites Rayonnement de surface à ambiant dans l’interface Transfert de chaleur dans des solides. La différence en matière de temps de calcul et l’influence sur les résultats étant négligeables, nous utiliserons ici l’approche plus précise passant par le calcul des facteurs de vue via l’interface Rayonnement de surface à surface.
Une attention particulière doit également être portée au maillage du dispositif. L’interface Faisceau radiatif en milieu absorbant résout une équation différentielle aux dérivées partielles du premier ordre et utilise, par défaut, une discrétisation linéaire des champs. En se référant aux coefficients d’absorption, nous savons que l’intensité va significativement varier à travers l’épaisseur des deux couches. Nous savons également que la variation d’intensité du profil du faisceau laser à la surface est assez progressive. Cela justifie l’utilisation d’un maillage structuré au sein des couches, avec des éléments rectangulaires de grand rapport d’aspect. Bien entendu, il sera toujours conseillé d’étudier la convergence du modèle en fonction de la finesse du maillage et de la tolérance relative du solveur à mesure que nous ferons évoluer la complexité de la modélisation, tel que présenté dans ce précédent article de notre blog “Intro to Modeling Transient Heating of Solids in COMSOL Multiphysics®”.
L’implémentation du modèle étant faite, nous allons résoudre le problème à l’aide du solveur temporel en stockant la solution aux pas pris par le solveur. Nous pouvons alors visualiser le profil de température et la chaleur absorbée, ainsi que la température au centre de la frontière supérieure du dispositif, tel qu’illustré ci-dessous.
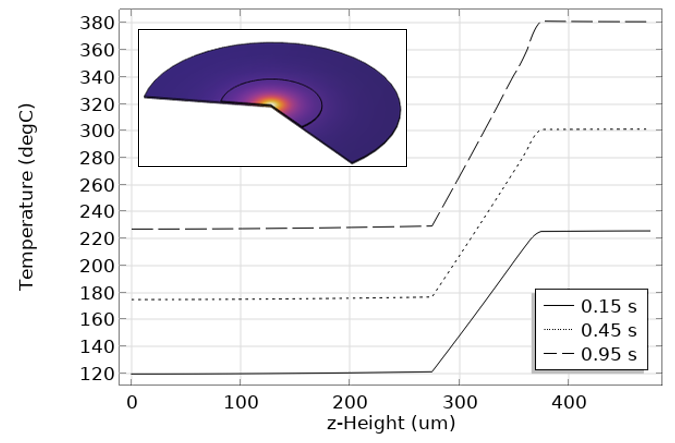
Evolution de la température en fonction de la coordonnée z.
Pour finir, nous allons ajouter une non-linéarité au matériau en faisant croître le coefficient d’absorption de la couche inférieure avec la température, pour illustration. La comparaison des coefficients d’absorption des deux matériaux semi-transparents est illustrée dans le graphique ci-dessous. L’introduction du coefficient d’absorption non-linéaire conduit à un échauffement plus important du matériau à mesure que la température augmente. L’ajout de cette non-linéarité au matériau requiert en outre de raffiner le maillage de la couche concernée.
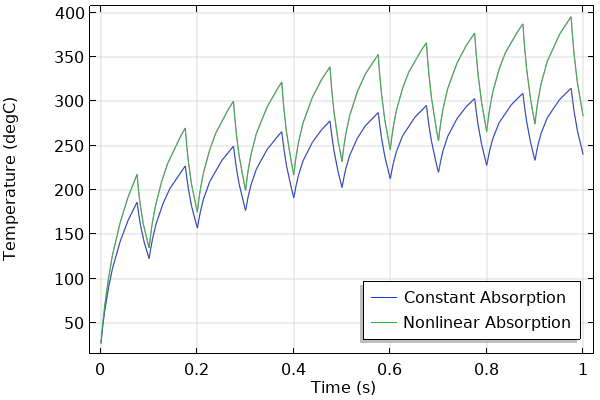
Comparaison de la température au cours du temps pour deux lois de comportement différentes.
Conclusion
Nous avons présenté une approche pour la modélisation du chauffage des matériaux semi-transparents. La source rayonnante collimatée, le laser, est modélisée à l’aide d’une combinaison d’interfaces Faisceau radiatif en milieu absorbant, permettant de traiter la nature semi-transparente du matériau à la longueur d’onde du laser, ainsi que les phénomènes de réflexion aux interfaces diélectriques. La source de chaleur pulsée est décrite par une interface Evènements, et la réémission infrarouge sur de plus grandes longueurs d’onde est modélisée via une interface Rayonnement de surface à surface. Cette stratégie de modélisation est applicable au traitement des semi-conducteurs, ou toute autre situation dans laquelle une lumière incidente collimatée frappe des matériaux semi-transparents.
Si ce type de simulations vous intéresse, vous pouvez télécharger le modèle présenté en guise d’exemple dans cet article en cliquant sur le bouton ci-dessous:







Commentaires (0)