
Le katana est un sabre légendaire qui a été utilisé pour la première fois par les samouraïs, il y a plusieurs siècles de cela. On le reconnaît principalement à sa forme incurvée et à son tranchant unique remarquablement aiguisé. Dans cet article de blog, nous verrons comment construire un modèle simple de katana à l’aide du logiciel COMSOL Multiphysics® et simuler un procédé de trempe différentielle afin de mieux comprendre certaines caractéristiques de ce sabre.
Table des matières
- Le célèbre katana
- Le module Metal Processing
- Le durcissement différentiel
- La multiphysique du traitement thermique
- Le matériau du katana
- La géométrie du katana
- Modélisation des transformations de phase:
- Propriétés matériaux mécaniques et thermiques
- Modélisation du transfert de chaleur:
- Modélisation des contraintes et des déformations
- Résultats
- Mettre en pratique ce que nous avons appris
Le célèbre katana
Peu d’armes sont aussi célèbres que le katana, l’arme de poing des guerriers samouraïs japonais. Réputée pour son tranchant et n’étant dégainée qu’en dernier recours, l’épée, et le lien presque sacré qui la rattache à son propriétaire, a inspiré plusieurs films, séries télévisées et livres contemporains. Dans Kill Bill: Volume 1 (2003) et Kill Bill: Volume 2 (2004), le personnage de ‘La mariée’, jouée par Uma Thurman, manie un katana dans la ville de Tokyo à notre époque. Dans le roman classique Shogun (1975) de James Clavell, le capitaine James Blackthorne est fait prisonnier par des samouraïs, après s’être échoué sur la côte japonaise.

Photographie d’un samouraï, prise par le photographe Felice Beato, vers 1860. Cette image est dans le domaine public aux États Unis parce que ses droits d’auteur au Japon ont expiré en 1971 et n’ont pas été rétablis par la loi relative aux accords du cycle d’Uruguay. Source: Britannica.
C’est évidemment entre les mains de ses utilisateurs que le katana a acquis ses lettres de noblesse. Mais comment les forgerons japonais fabriquaient-ils ces armes pour les samouraïs? Comment parvenaient-ils à trouver l’équilibre subtil entre les parties dures et souples de la lame, afin que le katana soit à la fois tranchant comme un rasoir et suffisamment ductile pour supporter des frappes répétées? Pourquoi la lame d’un katana est-elle courbée et non droite? Dans cet article, nous verrons comment modéliser le processus de durcissement différentiel d’un katana et en examinerons les effets pour mieux comprendre la fabrication de cette arme légendaire.
Le module Metal Processing
Le module Metal Processing, un produit complémentaire de COMSOL Multiphysics®, peut être utilisé pour modéliser les transformations de phase dans les alliages ferreux tels que les aciers, et dans les alliages de titane tels que le Ti-6Al-4V. Les applications comprennent la trempe de l’acier, pour modéliser par exemple le durcissement des pièces de transmission automobile, et la fabrication additive, pour modéliser les cycles répétés de refroidissement et de chauffage qui se produisent pendant l’impression. Les possibilités de modélisation des transformations de phase s’accompagnent de couplages avec la mécanique du solide et le transfert de chaleur, ce qui permet de prendre en compte des effets tels que la plasticité et la chaleur latente de la transformation de phase.
Le durcissement différentiel
Dans de nombreuses situations, il est souhaitable de ne durcir que certaines parties d’un composant. La trempe par induction en est un exemple. Un champ magnétique alternatif puissant est généré à l’aide de bobines électriques, ce qui induit des courants électriques à la surface du composant. Le composant est ensuite trempé et la zone de surface subit une transformation martensitique. Ce processus de durcissement différentiel est souvent utilisé pour les composants de transmission tels que les essieux et les engrenages afin d’augmenter la résistance à l’usure et à la fatigue.
La trempe à la flamme est un autre procédé qui peut être utilisé pour durcir la surface d’un composant. Au lieu d’un champ magnétique alternatif, la surface est chauffée localement par des flammes de gaz appliquées sur la surface avant de subir une trempe.
Bien entendu, la trempe par induction et la trempe à la flamme sont des procédés de traitement thermique relativement récents qui n’étaient pas à la disposition des forgerons japonais il y a plusieurs siècles. La fabrication traditionnelle du katana japonais faisait appel à un autre type de trempe différentielle. Pour un sabre de ce type, il est préférable que le tranchant de la lame soit dur – idéalement purement martensitique. L’arête de la lame doit quant à elle être de préférence ductile, par exemple perlitique, sans quoi le sabre risque de se briser à l’impact. La méthode traditionnelle de durcissement différentiel d’un katana consiste à appliquer de l’argile isolante sur la lame, afin de modifier le transfert de chaleur de l’acier chaud vers l’eau environnante lors de l’immersion. Différentes zones de la lame sont recouvertes d’argile de différentes épaisseurs. Près du tranchant, une couche d’argile plus fine est utilisée, tandis qu’une couche plus épaisse est appliquée sur les autres parties de la lame.
La multiphysique du traitement thermique
La simulation du traitement thermique d’une pièce en acier nécessite d’identifier les phénomènes physiques à inclure dans le modèle.
Fondamentalement, le processus est régi par le transfert de chaleur dû aux échanges thermiques avec l’extérieur. Le changement de température à l’intérieur du composant, en l’occurrence le katana, induit des transformations de phase métallurgiques (décomposition de l’austénite en ferrite, perlite, etc.). Lors des transformations de phase, il y a production de chaleur latente, ce qui a un impact sur les températures. Les changements de volume liés à la dilatation thermique et les différences de densité entre les phases entraînent des déformations du composant, ainsi que des contraintes mécaniques et des déformations plastiques. On sait que les transformations de phase qui se produisent en présence de contraintes mécaniques provoquent des déformations inélastiques dans le matériau, connues sous le nom de plasticité induite par la transformation (en anglais Transformation Induced Plasticity ou TRIP). Le processus de trempe est véritablement multiphysique par nature et, pour compliquer encore les choses, les phases métallurgiques individuelles ont des propriétés matériaux différentes, ce qui se traduit par un comportement moyen du matériau composite dépendant de la composition des phases.
Dans notre modèle de traitement thermique d’un katana, les simplifications suivantes ont été faites:
- La chaleur latente lors des transformations de phase est négligée
- Les déformations TRIP sont négligées
Le traitement thermique du katana est représenté dans la figure ci-dessous.
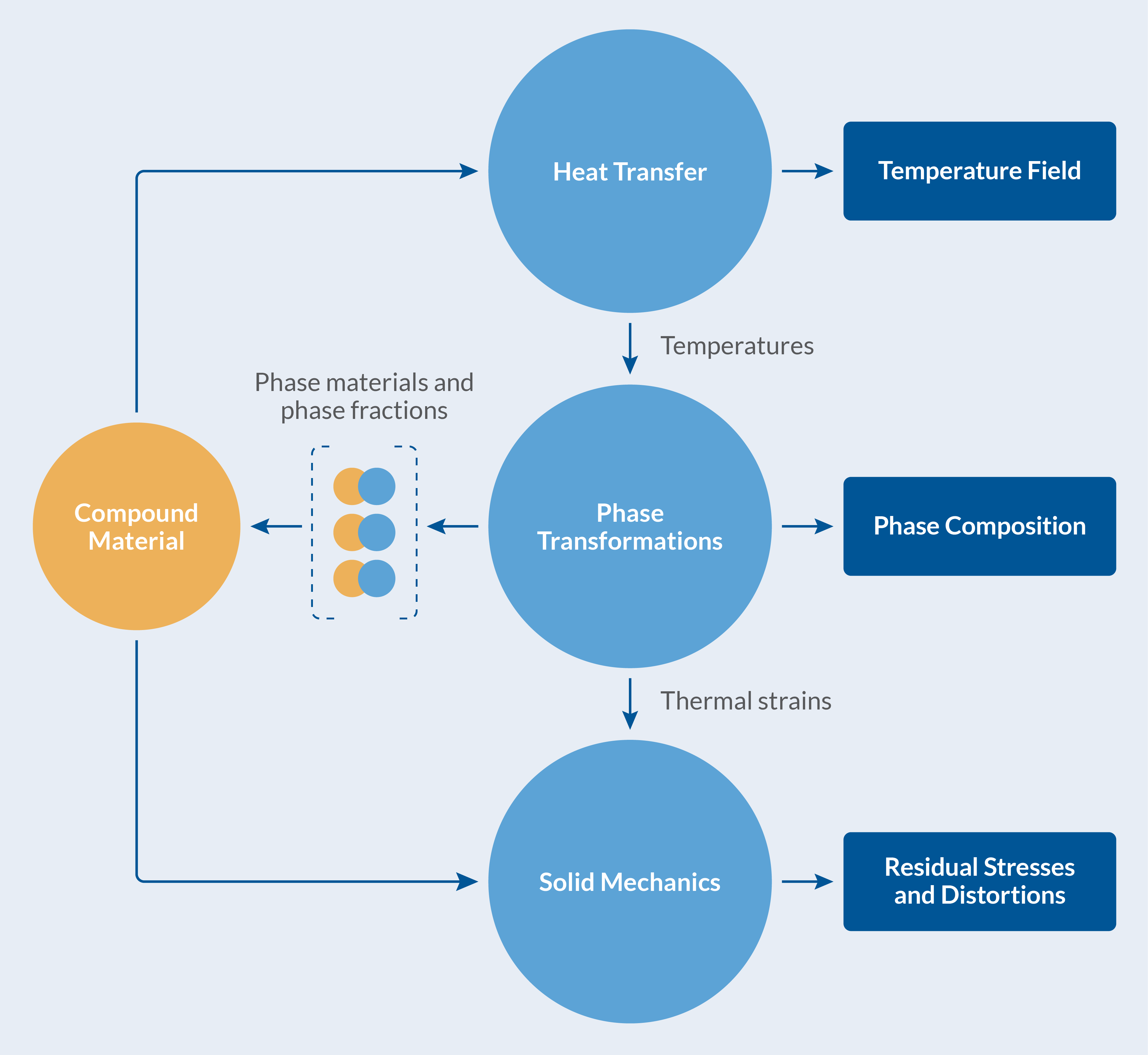 La multiphysique du traitement thermique d’un katana.
La multiphysique du traitement thermique d’un katana.
Le matériau du katana
La méthode traditionnelle de fabrication d’un katana consiste à utiliser différents types d’acier pour les différentes parties de la lame. En règle générale, le tranchant est différent du coeur de la lame, la différence la plus notable résidant dans la variation de la teneur en carbone. La quantité de carbone, ainsi que d’autres éléments d’alliage, influe fortement sur les propriétés thermiques et mécaniques de l’acier, ainsi que sur les caractéristiques de transformation de phase. Ici, une simplification est faite: un seul type d’acier a été utilisé. Sa composition en éléments d’alliage est indiquée dans le tableau ci-dessous:
| Élément | wt% |
|---|---|
| C | 0.63 |
| Mn | 0.9 |
| P | 0.04 |
En réalité, un acier contient d’autres éléments d’alliage, mais par souci de simplicité, nous ne considérons que le manganèse (Mn) et le phosphore (P), en plus du carbone (C).
La géométrie du katana
La géométrie du katana: la lame mesure 50 cm de long (à gauche) et la section de la lame mesure 2.8 cm de haut (à droite).
Modélisation des transformations de phase
Les différentes transformations de phase possibles doivent être caractérisées. A température ambiante, on considère que l’acier a une composition de base de 50% de ferrite et 50% de perlite. Le katana est d’abord chauffé jusqu’à ce que cette composition initiale soit entièrement transformée en austénite. Le katana est ensuite trempé dans l’eau pour obtenir une composition de phase finale. Cette composition variera dans l’espace et sera en général une combinaison de ferrite, de perlite, de bainite, de martensite et éventuellement d’austénite restante (voir la figure ci-dessous). La variation spatiale résulte de l’historique thermique en chaque point du matériau pendant le refroidissement.
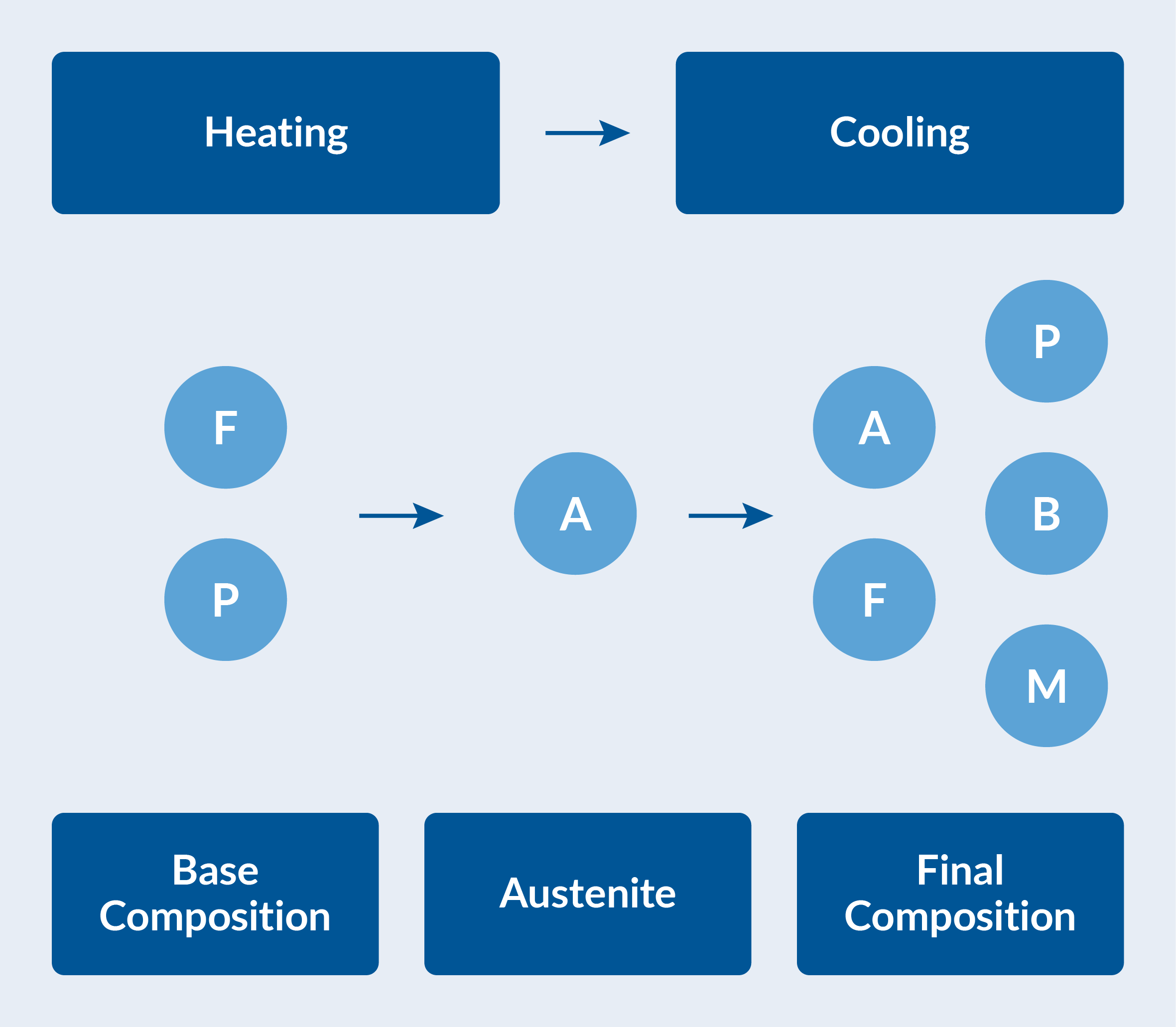
Composition des phases pendant le chauffage et le refroidissement. La composition de base comporte de la ferrite (F) et de la perlite (P), qui se transforment en austénite (A) lors du chauffage. L’austénite se décompose en ferrite, perlite, bainite (B) et martensite (M) pendant le refroidissement.
Chauffe
L’objectif principal de la simulation du chauffage est non seulement d’austénitiser l’acier ferrito-perlitique, mais aussi de modéliser la déformation thermique qui se développe lors du chauffage. Il est à noter que nous aurions pu omettre la partie chauffage du processus en appliquant une contrainte initiale au début du refroidissement pour inclure l’effet de la déformation thermique, mais nous avons choisi de modéliser le chauffage avant le refroidissement. Cependant, comme nous ne nous intéressons pas à la formation de l’austénite en tant que telle, nous utilisons le modèle de transformation de phase de Leblond–Devaux pour modéliser la formation de l’austénite à partir de la composition de base ferritique-perlitique. Le modèle de transformation de phase utilise un sous-noeud Source de phase additionnelle de sorte que la ferrite et la perlite agissent toutes deux comme des phases sources dans la formation de l’austénite. Les variations des fractions de phase de l’austénite (A), de la perlite (P) et de la ferrite (F) sont alors données par:
où la fraction de phase d’équilibre de l’austénite vaut 1 (austénitisation complète) et où la constante de temps est fixée à 60 secondes:
En outre, nous n’autorisons cette transformation de phase que pendant le chauffage, ce qui est spécifié à l’aide du sous-noeud Condition de transformation où la condition suivante c est introduite:
audc.Tt>0
Refroidissement
Lorsque le katana entièrement austénitique est trempé dans l’eau, l’austénite se décompose en une combinaison de ferrite, de perlite, de bainite et de martensite. En fonction de la vitesse de refroidissement en différents points de la lame, les phases se forment en quantités différentes. Cela suggère que des descriptions plus détaillées des transformations de phase sont nécessaires pour le refroidissement, à la différence de l’étape de chauffe. Les décompositions de l’austénite en ferrite, perlite et bainite sont donc modélisées à l’aide du modèle de transformation de phase Johnson-Mehl-Avrami-Kolmogorov (JMAK). Il s’agit d’un modèle adapté à la modélisation des transformations de phase diffusives. Il comporte trois paramètres:
- La fraction de phase à l’équilibre, \xi_\mathrm{eq}
- La constante de temps, \tau
- L’exposant d’Avrami, n
La fraction de phase à l’équilibre désigne la fraction de phase de destination à l’équilibre, et peut être vue comme une valeur asymptote à long terme. Par exemple, la fraction de phase d’équilibre de la ferrite entre les températures A_{e1} et A_{e3} peut être évaluée en appliquant la règle des bras de levier à la région biphasée de l’austénite et de la ferrite dans un diagramme Fe-C. Pour déterminer les paramètres restants, nous pouvons utiliser un diagramme temps-température-transformation (ou diagramme TTT), qui indique typiquement les moments où chaque phase métallurgique commence à se former et où chaque transformation prend fin. Le diagramme TTT suppose des conditions isothermes, ce qui signifie que si un diagramme TTT doit être obtenu expérimentalement, une éprouvette doit d’abord être rapidement refroidie à une “température cible” T_\mathrm{0}, puis maintenue à cette température. Ce processus est ensuite répété sur une plage de températures allant généralement de la température d’austénitisation à la température de formation de la martensite.
Dans le schéma ci-dessous, la partie inférieure montre un diagramme TTT dans lequel deux courbes indiquent les temps nécessaires pour former 1 % et 99 % de la phase de destination. Ces fractions sont des fractions de phase relatives, c’est-à-dire qu’elles représentent, à chaque niveau de température, la fraction de la phase de destination par rapport à ce qui est maximalement atteignable à cette température. La fraction de phase relative est donnée par X =\xi^\mathrm{d}/\xi^\mathrm{d}_\mathrm{eq}, où la fraction de phase d’équilibre dépend généralement de la température. Notez que si ces deux courbes TTT ont été établies expérimentalement, le modèle de transformation de phase JMAK peut être ajusté précisément, pour chaque température. Les fractions de phase relatives intermédiaires seront ainsi dictées par la formulation du modèle JMAK lui-même. La partie supérieure du schéma montre l’évolution de la phase de destination telle qu’elle est régie par un modèle de transformation de phase spécifique, à T=T_0.
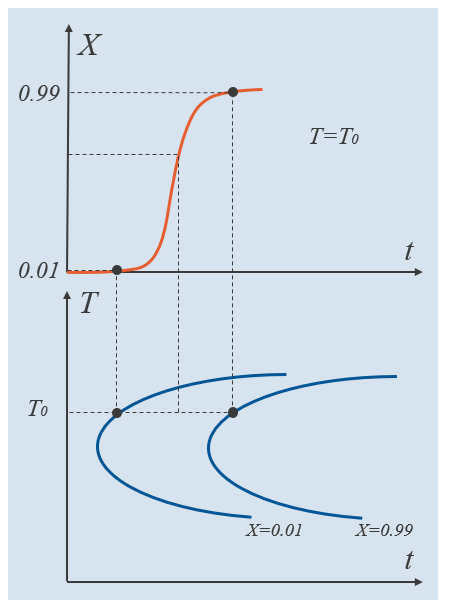
Exemple de courbes TTT pour des fractions de phase relatives de 0.01 et 0.99. Une fraction de phase relative intermédiaire est également représentée.
Dans COMSOL Multiphysics®, le modèle de transformation de phase JMAK est formulé en termes de vitesses de transformation, ce qui le rend adapté aux conditions non isothermes. Au sens du diagramme TTT, cependant, nous pouvons intégrer le modèle JMAK de manière symbolique. L’évolution de la phase de destination dans le temps s’écrit alors:
Après quelques modifications, cette équation peut être réécrite de la façon suivante:
Si nous utilisons les temps de départ et de fin et les fractions de phase de la figure ci-dessus, en supposant que la fraction de phase d’équilibre soit connue, nous pouvons identifier l’exposant d’Avrami n et la constante de temps \tau:
C’est précisément ce qui est fait pour la formulation données du diagramme TTT du modèle de transformation de phase JMAK dans le noeud Transformation de phase.
Dans notre modèle de trempe d’un katana, trois séries de courbes TTT de départ et de fin, fictives mais réalistes, sont utilisées pour décrire la décomposition de l’austénite en ferrite, perlite et bainite, respectivement. Voici une partie des données utilisées pour la ferrite:
| T \, (^{\circ}C) | t_1 \, (s) | t_{99} \, (s) |
|---|---|---|
| 575 | 2.2 | 43 |
| 580 | 0.22 | 2.1 |
| 585 | 0.075 | 1.42 |
| 590 | 0.076 | 1.47 |
| 595 | 0.078 | 1.47 |
| 600 | 0.079 | 1.49 |
| 605 | 0.081 | 1.54 |
| 610 | 0.084 | 1.58 |
| 615 | 0.086 | 1.63 |
| 620 | 0.090 | 1.70 |
| \vdots | \vdots | \vdots |
| \vdots | \vdots | \vdots |
| 730 | 5.8 | 110 |
| 735 | 13 | 254 |
| 740 | 41 | 820 |
| 745 | 322 | 6246 |
Pour compléter les définitions du modèle de transformation de phase, nous devons également identifier:
- Les fractions de phase d’équilibre en fonction de la température pour la ferrite, la perlite et la bainite, pour les transformations de phase correspondantes.
- Les limites supérieures et inférieures de température pour la transformation de phase. Par exemple, A_\mathrm{e3} définit le début de la transformation ferritique, and M_\mathrm{s} est la température de début de formation de la martensite.
Les fractions de phase d’équilibre et les différentes températures de transformation sont calculées à partir de la composition chimique grâce au noeud Composition de l’acier de l’interface Décomposition austénitique.
Nous n’autorisons ces transformations de phase que pendant le refroidissement et, comme pour la chauffe, nous imposons cela à l’aide du sous-nœud Condition de transformation dans lequel la condition suivante c est introduite:
audc.Tt<=0
Lorsque les courbes TTT pour la transformation de phase en ferrite, perlite et bainite sont utilisées conjointement, nous pouvons calculer un diagramme TTT en utilisant l’interface Décomposition austénitique. La figure ci-dessous montre le diagramme TTT calculé. Pour modéliser cela, nous utilisons l’interface Décomposition austénitique en 0D, et les temps pour atteindre certaines fractions de phase sont obtenus en sélectionnant Calculer les temps de transformation dans les noeuds de phase.
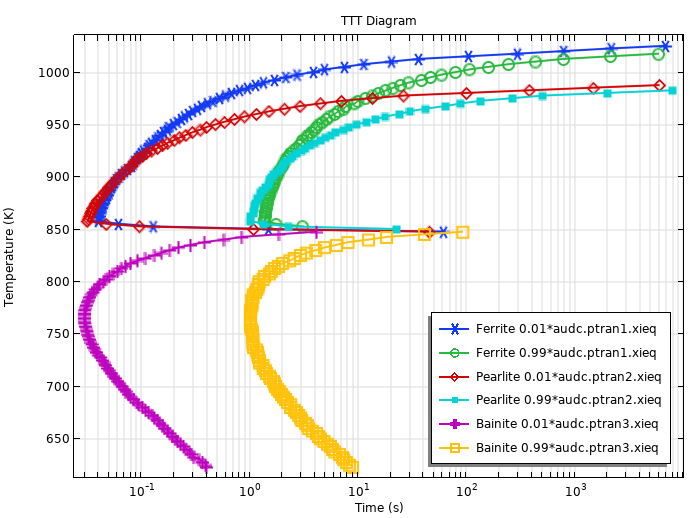
Diagramme TTT calculé à partir des données TTT fictives.
La transformation de phase martensitique est décrite par le modèle de transformation de phase Koistinen-Marburger. Ce modèle utilise deux paramètres:
- Le coefficient de Koistinen–Marburger, \beta
- La température de début de la transformation en martensite, M_\mathrm{s}
Contrairement aux transformations diffusives ferritiques, perlitiques et bainitiques pour lesquelles on considère dans des conditions isothermes, la transformation martensitique est intrinsèquement dépendante de la vitesse de refroidissement. La vitesse de formation de la martensite, selon le modèle de Koistinen–Marburger, est proportionnelle à la vitesse de refroidissement de par le coefficient \beta.
Une fois toutes les transformations de phase définies, nous pouvons également calculer un diagramme de transformations en refroidissement continu (CCT). La figure ci-dessous montre un diagramme CCT, où la température d’austénitisation est de 900°C, et les vitesses de refroidissement vont de 0.1 K/s à 1000 K/s. Les courbes à 1 % sont représentées pour les phases formées de ferrite, perlite, bainite et martensite. La courbe à 1 % de l’austénite, également visible, peut être considéré comme l’achèvement de la décomposition de l’austénite — la quasi-totalité de l’austénite ayant été décomposée en d’autres phases.
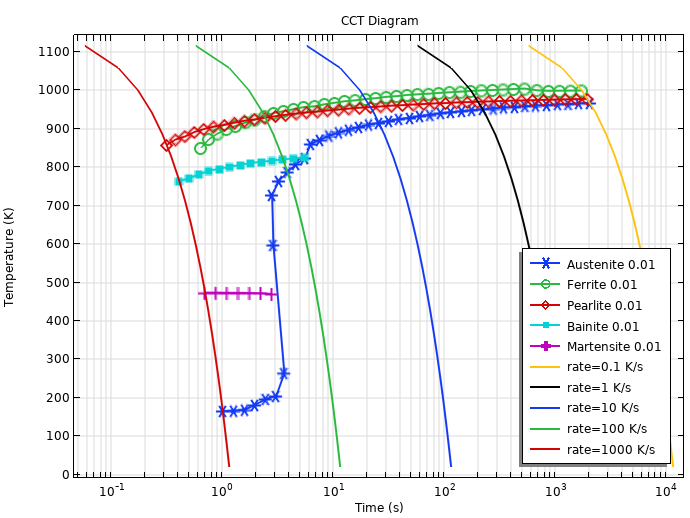
Diagramme CCT calculé à partir des données TTT.
Propriétés matériaux mécaniques et thermiques
Pour mettre en place un modèle détaillé de la trempe d’une pièce en acier telle qu’un katana, il est nécessaire de disposer de propriétés thermiques et mécaniques. Ces propriétés varient selon les phases, telles que l’austénite et la ferrite, et dépendent en outre de la température. Pour les propriétés élastoplastiques, il existe généralement aussi une dépendance à la déformation et éventuellement à la vitesse de déformation. Obtenir expérimentalement un ensemble complet de propriétés des matériaux est long et coûteux, et donc souvent inenvisageable. Dans la pratique, d’autres sources sont utilisées, notamment des données expérimentales tirées de la littérature et des propriétés de matériaux calculées. L’objectif de la présente simulation est de simuler la trempe d’un katana et, dans cette optique, nous avons procédé aux simplifications de modélisation suivantes:
- Les propriétés élastiques sont communes aux différentes phases, mais les autres propriétés sont considérées comme différentes d’une phase à l’autre.
- Les conductivités thermiques et les capacités calorifiques sont considérées comme étant dépendantes de la température.
- Les limites d’élasticité initiales sont considérées comme dépendant de la température.
- Les comportements d’écrouissage des phases sont considérés comme linéaires et isotropes, et dépendent de la température.
- Les coefficients de dilatation thermique sont constants, mais les températures de référence du volume varient.
Les propriétés matériaux de chaque phase, ainsi que l’évolution de la composition des phases (fractions de phase), sont utilisées pour calculer les propriétés matériaux effectives. Cela est fait automatiquement dans le module Metal Processing, et les propriétés effectives calculées sont regroupées dans un Matériau composite pour être utilisées de manière transparente par d’autres interfaces physiques (voir la figure ci-dessous).
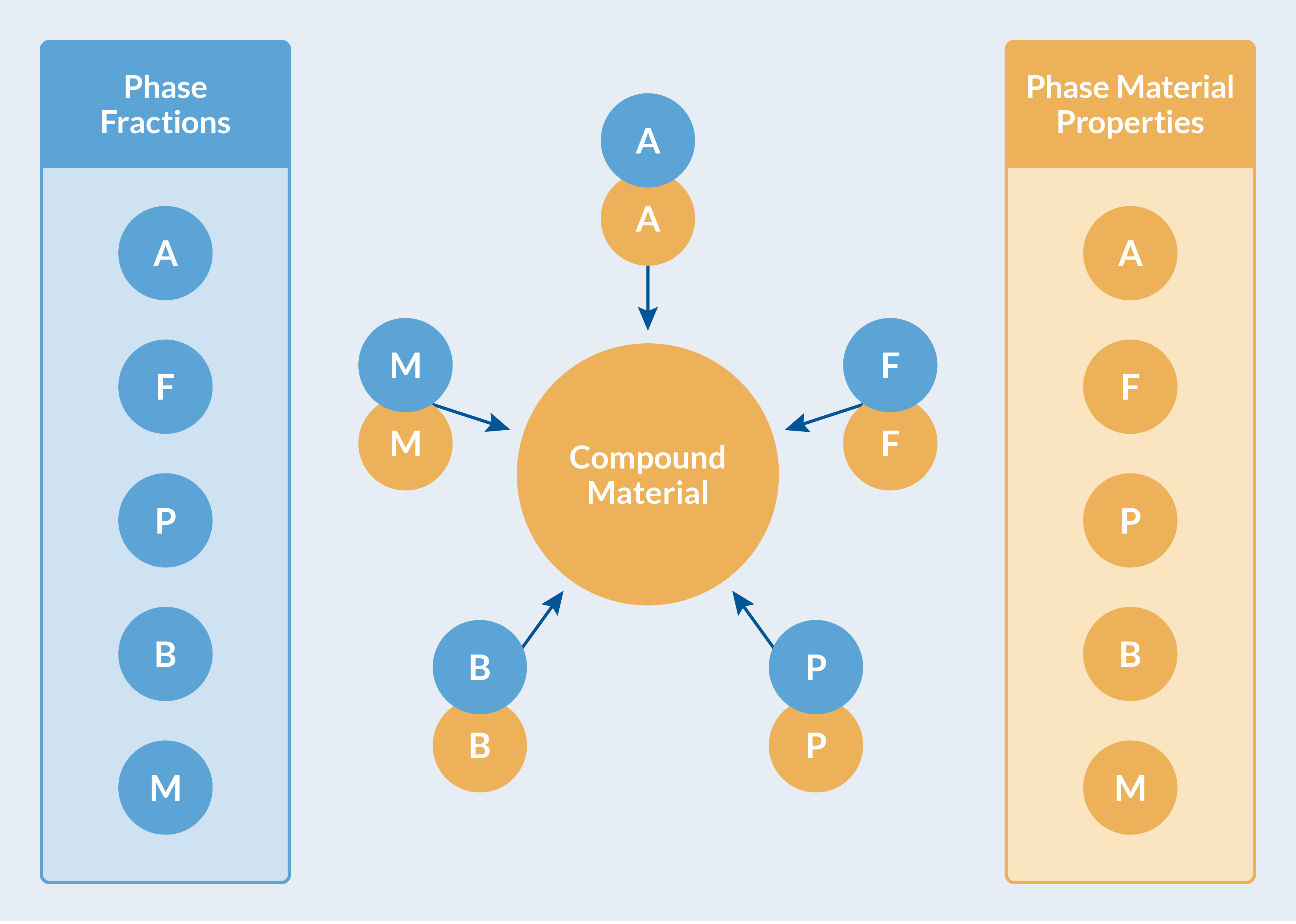
Les propriétés matériaux effectives calculées sont regroupées dans un Matériau composite.
Modélisation du transfert de chaleur
L’interface Transfert de chaleur dans les solides est utilisée pour modéliser le transport de chaleur dans le katana et les échanges de chaleur avec l’environnement. Pour simplifier les choses, le rayonnement est négligé et le transfert de chaleur de la lame vers le milieu environnant est modélisé en considérant uniquement la convection. Pour cela, on impose à la surface de la lame un flux de chaleur caractérisé par un coefficient d’échange thermique dépendant de la température.
Chauffe
La chauffe du katana a pour but d’austénitiser la composition ferrito-perlitique de base. Pour modéliser cela, nous utilisons un modèle simplifié pour la convection faisant appel à un coefficient d’échange thermique constant de 300 W/m^2K. La température ambiante est portée de la température ambiante à 850°C pendant la première minute de chauffage, puis maintenue constante pendant toute la durée de la chauffe. La durée totale est choisie de manière à ce que le matériau se transforme entièrement en austénite, et le chauffage est réalisé de manière à ce que les gradients thermiques dans le katana soient suffisamment faibles pour empêcher toute déformation plastique induite thermiquement.
Refroidissement
Pour prendre en compte l’influence des différentes épaisseurs de l’argile isolante, on utilise des coefficients de transfert de chaleur différents pour la région proche du tranchant de la lame et la partie supérieure de la lame. La figure ci-dessous montre les coefficients d’échange thermique en fonction de la température qui ont été utilisés pour représenter les couches d’argile fines et épaisses.
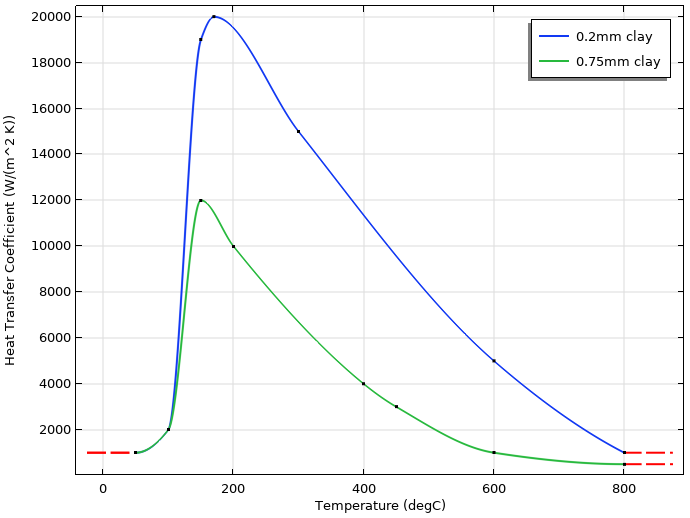
Coefficients d’échange thermique en fonction de la température pour les couches d’argile mince (0.2 mm) et plus épaisse (0.75 mm). La couche mince est appliquée sur le tranchant, tandis que la couche plus épaisse est appliquée sur le reste de la lame.
Modélisation des contraintes et des déformations
L’interface Mécanique du solide est utilisée pour calculer les contraintes, les déformations et les distorsions du katana durant le transitoire thermique auquel il est soumis. Nous avons souligné précédemment le fait que la dilatation thermique et les différences de densité entre les phases engendrent des déformations du composant, ainsi que des contraintes mécaniques et des déformations plastiques. Ces effets sont traités par l’interface Décomposition austénitique et transmis à l’interface Mécanique du solide par le couplage multiphysique Déformation de transformation de phase. Nous nous attendons à une flexion importante du katana. La flexion d’une structure élancée ne produit pas nécessairement de grandes déformations du matériau, cependant, elle implique des rotations finies et l’analyse est donc géométriquement non linéaire. La flexion devrait également induire des déformations plastiques, qui sont prises en compte par le sous-noeud Plasticité de la loi de comportement Matériau élastique linéaire.
Résultats
L’une des caractéristiques les plus remarquables du katana est la courbure de sa lame. Ce qui est intéressant, c’est que cette courbure résulte directement du processus de trempe et non d’une flexion qui aurait été effectuée avant le traitement thermique de la lame. La lame étant plus fine près du tranchant, là où la couche d’argile isolante est également plus fine, la température baisse rapidement et la lame se courbe d’abord vers le bas à mesure que l’austénite refroidit et se contracte. Lorsque la température passe en dessous de la température de début de formation de la martensite, l’austénite commence à se transformer en martensite. Cette transformation s’accompagne d’une expansion volumétrique qui provoque des contraintes de compression sur le tranchant de la lame. À mesure que le refroidissement progresse vers le dos de la lame, la vitesse de refroidissement diminue et d’autres phases métallurgiques apparaissent. La courbure initiale de la lame vers le bas laisse place à la forme courbée traditionnelle de l’épée. La figure du bas montre la composition finale des phases métallurgiques. On remarque notamment que le tranchant est martensitique, et donc dur, mais que le dos de la lame est en grande partie perlitique, et donc beaucoup plus ductile.
Fraction de phase de la martensite (en haut), contrainte axiale (au centre) et température (en bas) durant le refroidissement.
La composition finale après trempe. Le tranchant présente la structure martensitique dure souhaitée, et le dos de la lame est en grande partie perlitique.
Mettre en pratique ce que nous avons appris
Dans cet article de blog, nous avons montré comment effectuer une simulation de trempe d’un katana en utilisant COMSOL Multiphysics®. Nous avons expliqué comment le katana obtient sa forme incurvée et comment une version simplifiée du procédé traditionnel de trempe différentielle à l’argile produit une lame avec un tranchant dur et un coeur mou. Si nous avons mis en place ce modèle par simple curiosité, nous avons toutefois pu montrer que COMSOL Multiphysics® peut être utilisé pour réaliser des simulations générales de durcissement de l’acier, qui permettent de calculer non seulement la composition des phases métallurgiques, mais aussi de prévoir les distorsions et les contraintes résiduelles.
À votre tour!
Vous voulez essayer de modéliser la trempe différentielle d’un katana? Les fichiers du modèle sont disponibles dans la Bibliothèques d’applications.




Commentaires (0)