
Modéliser la convection naturelle et la convection forcée avec COMSOL Multiphysics®
Chaque fois qu’une pièce chauffée ou refroidie est exposée à l’air, il y a un transfert de chaleur de la pièce vers l’air par convection. Le mouvement de l’air peut être soit forcé, par l’intermédiaire d’un ventilateur, soit libre, en raison des variations naturelles de flottabilité dues aux changements de température de l’air. Aujourd’hui, nous allons examiner plusieurs méthodes permettant de modéliser ces types de convection dans le logiciel COMSOL Multiphysics®.
Une approche simple : le coefficient d’échange thermique
Commençons par examiner un modèle de chauffage électrique d’un busbar, illustré ci-dessous. Vous reconnaîtrez peut-être cet exemple comme étant le modèle d’introduction à COMSOL Multiphysics®, mais si vous ne l’avez pas encore étudié, nous vous encourageons à le consulter en lisant le document PDF d’Introduction à COMSOL Multiphysics®.
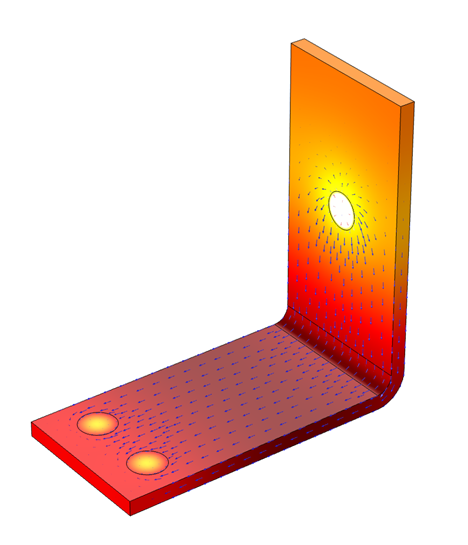
Les courants électriques (flèches) qui circulent dans un busbar métallique conduisent à un chauffage résistif provoquant une augmentation de la température (surface colorée).
Dans cet exemple, nous modélisons un courant électrique circulant dans un busbar. Il en résulte un échauffement résistif qui entraîne une augmentation de la température dans celui-ci. Nous supposons qu’il y a uniquement un transfert de chaleur vers l’air ambiant, en négligeant tout transfert de chaleur par conduction à travers les boulons et tout transfert de chaleur par rayonnement. L’exemple suppose également qu’il n’y a pas de ventilateur forçant l’écoulement de l’air autour du busbar. Le transfert de chaleur vers l’air se fait donc par convection naturelle ou libre.
Lorsque la pièce chauffe l’air environnant, celui-ci devient plus chaud. À mesure que l’air devient plus chaud, sa densité diminue, ce qui fait que l’air chaud monte par rapport à l’air environnant plus froid. Ces courants d’air convectifs libres augmentent le taux de transfert de chaleur de la pièce vers l’air ambiant. Les courants d’air dépendent des variations de température ainsi que de la géométrie de la pièce et de son environnement. Bien entendu, la convection peut également se produire dans tout autre gaz ou liquide, comme l’eau ou l’huile d’un transformateur, mais nous nous intéresserons principalement à la convection dans l’air.
Nous pouvons classer le milieu aérien environnant en deux catégories : Interne ou Externe. “Interne” signifie qu’il existe une cavité de taille finie (telle qu’une boîte de jonction électrique) autour de la pièce dans laquelle l’air est raisonnablement bien contenu, bien qu’il puisse y avoir des entrées et sorties d’air connues vers un espace extérieur. Nous supposons alors que les conditions limites thermiques vers l’extérieur de la cavité et aux entrées et sorties sont connues. D’autre part, le terme “externe” implique que l’objet est entouré principalement d’un volume d’air infiniment grand. Nous supposons alors que la température de l’air loin de l’objet a une valeur constante et connue.
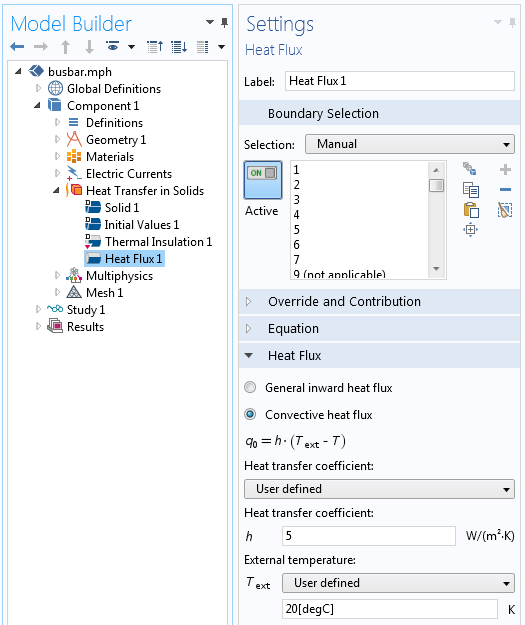
Les réglages correspondant à un coefficient d’échange thermique constant.
L’exemple introductif du busbar suppose un transfert de chaleur par convection naturelle vers un milieu externe. Ce phénomène est modélisé à l’aide de la condition aux limites suivante pour le flux de chaleur :
où Text = 25°C désigne la température externe de l’air et h=5 W/m^2K est le coefficient d’échange thermique (aussi appelé coefficient de transfert thermique).
Ce coefficient d’échange thermique à valeur unique représente une moyenne approximative de toutes les variations locales des mouvements d’air. Même dans le cas de ce système simple, toute valeur comprise entre h\approx 2-25 W/m^2K pourrait être un coefficient d’échange thermique approprié, et il vaut la peine d’essayer les cas limites et de comparer les résultats. Si nous savons en revanche qu’un ventilateur souffle de l’air au-dessus de cette structure, nous pouvons alors utiliser un coefficient d’échange thermique de h\approx 10-250 W/m^2K pour tenir compte de la hausse du transfert de chaleur, en raison de la vitesse plus élevée de l’air.
Lorsque le fluide environnant est un liquide tel que l’eau, la plage de valeurs des coefficients d’échange thermique, en convection naturelle ou forcée, est beaucoup plus large. Pour la convection naturelle dans un liquide, l’intervalle est typiquement h\approx 50-1000 W/m^2K. Pour la convection forcée, l’intervalle est bien plus large : h\approx 50-20000 W/m^2K.
Il est évident que la saisie d’un coefficient d’échange thermique à valeur unique pour la convection naturelle ou forcée est une simplification excessive, alors pourquoi y avoir recours ? Tout d’abord, c’est simple à mettre en œuvre et il est facile de comparer les cas extrêmes. De plus, cette condition aux limites est disponible dans la plateforme de base COMSOL Multiphysics®. Cependant, des approches plus sophistiquées sont disponibles dans le module Heat Transfer et le module CFD, que nous allons donc aborder maintenant.
Utiliser une corrélation pour la convection
Une corrélation est une relation empirique qui a été développée pour calculer les coefficients d’échange thermique par convection sur des géométries courantes. Lorsque vous utilisez le module Heat Transfer ou le module CFD, ces corrélations sont disponibles dans la condition aux limites de flux de chaleur, comme le montre la capture d’écran ci-dessous.
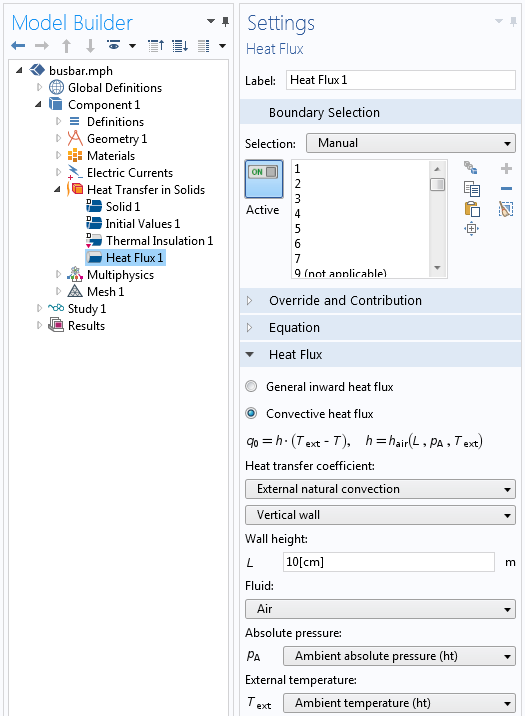
La condition aux limites Flux de chaleur avec la corrélation de convection naturelle externe pour une paroi verticale.
L’utilisation de ces corrélations nécessite de renseigner les dimensions caractéristiques de la pièce. Par exemple, dans notre modèle de busbar, nous utilisons la corrélation Convection naturelle externe, paroi verticale et spécifions une hauteur de paroi de 10 cm pour modéliser le flux de chaleur par convection naturelle sur les faces verticales du busbar. Nous devons également spécifier la température et la pression de l’air ambiant. Ces valeurs peuvent être importées à partir de la base de données de l’ASHRAE, une procédure que nous décrivons dans un précédent billet de blog.
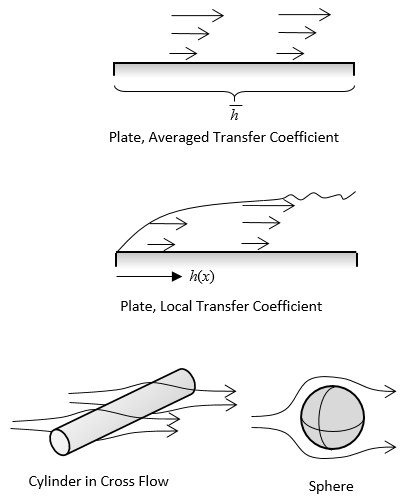
Le tableau ci-dessous présente les schémas de toutes les corrélations disponibles. Les informations sur la géométrie, associées à une une corrélation du nombre de Nusselt, permettent de déterminer un coefficient d’échange thermique. Pour les faces parallèles du busbar, nous utilisons par exemple les corrélations Plaque horizontale, face supérieureet Plaque horizontale, face inférieure.
Lorsque vous utilisez les corrélations de convection forcée, vous devez également introduire la vitesse de l’air. Ces corrélations ont l’avantage d’être une représentation plus précise de la réalité, puisqu’elles sont basées sur des données expérimentales bien établies. Elles conduisent à une condition aux limites non linéaire, mais n’entraînent généralement pas d’augmentation significative des temps de calcul, comparé à un coefficient de transfert de chaleur constant. Toutefois, elles ne peuvent être utilisées que lorsqu’il existe une relation empirique adaptée à la géométrie de la pièce.
| Convection naturelle | Convection forcée | |
|---|---|---|
| Externe | 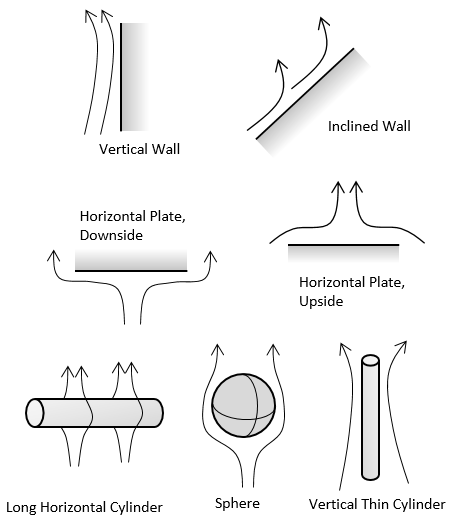 |
 |
| Interne | 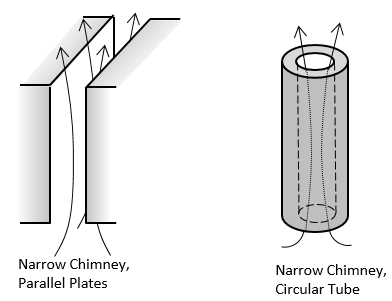 |
 |
Les corrélations pour la convection disponibles dans les conditions limites.
Il convient de noter que toutes les corrélations ci-dessus, même celles qualifiées d’internes, supposent la présence d’un réservoir externe infini de fluide, par exemple l’air ambiant. La chaleur évacuée par les surfaces est transférée à cet air ambiant sans en modifier la température, qui est par ailleurs connue. Cependant, si nous nous intéressons à la convection dans un volume complètement fermé, aucune de ces corrélations n’est valable et nous devons opter pour une approche de modélisation différente.
Approximer la convection naturelle dans une cavité à l’aide de la conductivité augmentée par convection
Considérons une cavité rectangulaire emplie d’air. Quand cette cavité est chauffée sur l’un de ses côtés verticaux et refroidie sur l’autre, une circulation continue de l’air est observée. De même, il y aura une circulation d’air si la cavité est chauffée par le bas et refroidie par le haut. Ces cas sont illustrés dans les figures ci-dessous, qui ont été générées en résolvant à la fois le champ de température et l’écoulement de l’air.
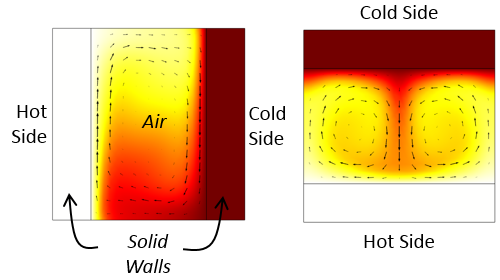
Courants de convection naturelle dans des cavités rectangulaires orientées verticalement et horizontalement.
La résolution des écoulements de convection naturelle est assez complexe (voir, par exemple, cet article de blog sur la modélisation de la convection naturelle). C’est pourquoi il peut être intéressant d’opter pour une alternative plus simple. Dans le module Heat Transfer, il est possible d’utiliser la fonctionnalité de Conductivité augmentée par convection. Lorsque cette fonctionnalité est utilisée, la conductivité thermique effective de l’air est augmentée selon des corrélations applicables aux cas de cavités rectangulaires horizontales et verticales, comme le montre la capture d’écran ci-dessous.
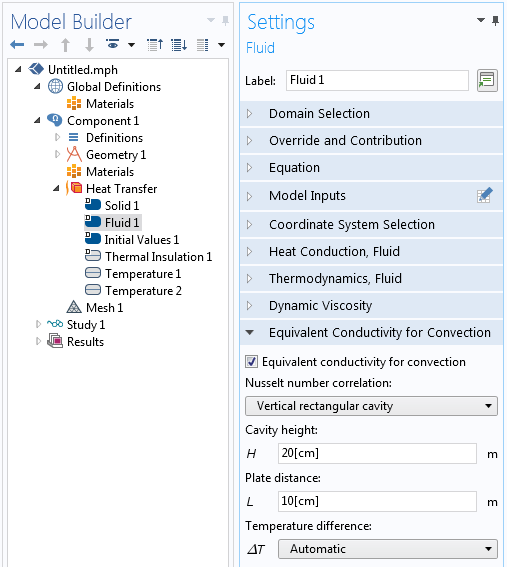
Réglages de la fonctionnalité de conductivité augmentée par convection.
Le domaine d’air est toujours explicitement modélisé à l’aide d’un noeud Fluide dans l’interface de Transfert de chaleur, mais l’écoulement n’est pas pris en compte et le terme de vitesse est simplement négligé. La conductivité thermique est augmentée par un facteur de corrélation empirique qui dépend des dimensions de la cavité et de l’écart de température de part et d’autre de la cavité. Les dimensions de la cavité doivent être spécifiées, mais le logiciel peut automatiquement déterminer et mettre à jour l’écart de température à travers la cavité.
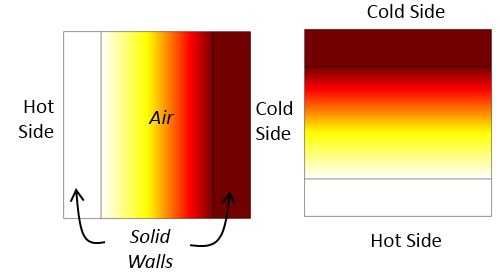
Distribution de la température dans des cavités orientées verticalement et horizontalement en utilisant la conductivité augmentée par convection. Les courants d’air convectifs libres ne sont pas calculés. En revanche, la conductivité thermique de l’air est augmentée.
Cette approximation de la convection naturelle dans une cavité complètement close nous oblige à mailler le domaine de l’air et à résoudre le champ de température dans l’air, mais cela ne représente en général qu’un faible coût de calcul. L’inconvénient de cette approche est qu’elle n’est pas très adaptée aux géométries non rectangulaires.
Approximer la convection forcée dans une cavité à l’aide de domaines isothermes
Considérons ensuite une enceinte complètement hermétique, mais contenant un ventilateur ou une soufflerie pour brasser l’air. On peut raisonnablement supposer que l’air bien mélangé présente une température uniforme dans l’ensemble de la cavité. Dans ce cas, il convient d’utiliser la fonctionnalité de Domaine isotherme, qui est disponible avec le module Heat Transfer lorsque l’option Domaine isotherme est sélectionnée dans la fenêtre de réglages.
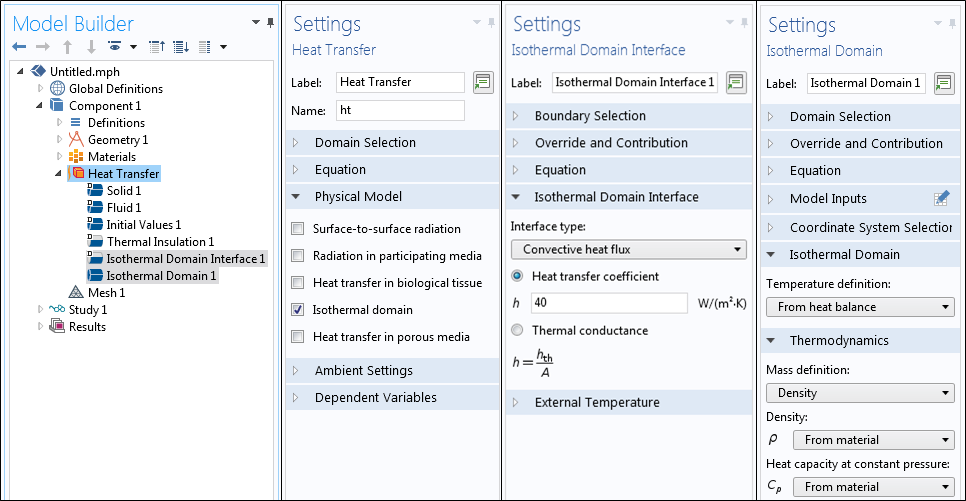
Les réglages associés à l’utilisation de la fonctionnalité Domaine isotherme.
Un domaine d’air bien mélangé peut être explicitement modélisé à l’aide de la fonctionnalité Domaine isotherme. Dans le modèle, la température de l’air est supposée constante sur l’ensemble du domaine et est calculée à partir du bilan de chaleur entrante et sortante par les frontières du domaine isotherme. Ces dernières peuvent être définies selon l’une des options suivantes :
- Isolation thermique: aucun transfert de chaleur à travers la frontière
- Continuité: continuité de la température à travers la frontière
- Ventilation: un débit massique connu de fluide, de température connue, entrant ou sortant du domaine isotherme
- Flux de chaleur convectif: un coefficient d’échange thermique défini par l’utilisateur, comme décrit précédemment
- Contact thermique: une résistance thermique spécifique
De toutes ces options de conditions limites, le Flux de chaleur convectif est le choix le plus approprié pour modéliser un volume d’air bien mélangé dans une cavité fermée.
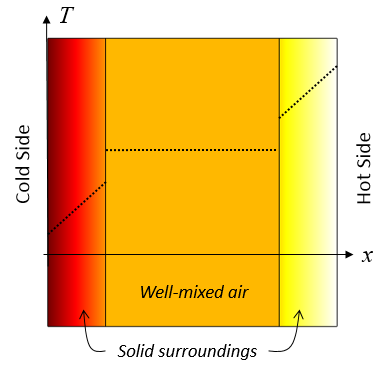
Résultats typiques de l’utilisation d’un domaine isotherme. Le domaine d’air bien mélangé présente une température uniforme. Le transfert de chaleur vers les domaines solides adjacents est décrit par un coefficient d’échange thermique spécifié.
Modéliser explicitement l’écoulement d’air
L’approche la plus coûteuse en termes de calcul, mais aussi la plus générale, consiste à modéliser explicitement l’écoulement d’air. On peut ainsi modéliser à la fois la convection forcée et la convection naturelle, que ce soit pour un écoulement interne ou externe. Ce type de modélisation peut être réalisé avec le module Heat Transfer ou le module CFD.
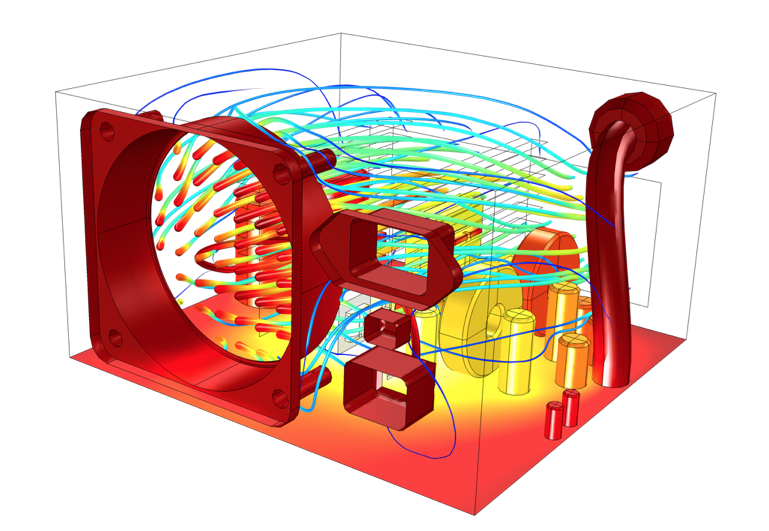
Un exemple de calcul de l’écoulement d’air et de la température dans un boîtier électronique.
Si vous avez suivi le guide d’Introduction à COMSOL Multiphysics®, vous avez déjà résolu un exemple de modèle de convection forcée interne. Vous pouvez en apprendre davantage sur la modélisation explicite dans les ressources mentionnées à la fin de ce billet de blog.
Quand peut-on totalement ignorer la convection naturelle ?
Nous terminerons ce sujet en abordant la question suivante : quand peut-on ignorer la convection naturelle ? Et dans ce cas là, quelle approche de modélisation peut-on adopter ? Lorsque les dimensions d’une cavité sont très faibles, comme dans le cas d’un interstice entre deux pièces ou d’un tube très fin, il est possible que l’amortissement visqueux soit plus important que les forces de flottabilité. Cet équilibre entre les forces visqueuses et les forces de flottabilité est caractérisé par le nombre adimensionnel de Rayleigh. L’apparition de la convection naturelle dépend beaucoup des conditions aux limites et de la géométrie. On peut considérer en règle générale que pour des dimensions inférieures à 1 mm, il n’y aura probablement pas de convection naturelle, mais qu’au-delà de 1 cm, il est probable que des mouvements d’air apparaissent.
Comment pouvons-nous donc modéliser le transfert de chaleur à travers ces interstices ? S’il n’y a pas d’écoulement d’air, ces régions peuvent simplement être modélisées comme un solide ou un fluide sans terme de convection. Cela est illustré dans le tutoriel Performances thermiques des fenêtres et des vitrages. Il convient également de modéliser l’air comme un solide dans toute structure fermée microscopique.
Si ces interstices sont très minces par rapport aux autres dimensions du système analysé, vous pouvez les simplifier davantage en les modélisant par des conditions aux limites de Couche mince de type Approximation de grande épaisseur thermique. Cette condition aux limites introduit un saut de température à travers la frontière, fonction de l’épaisseur et de la conductivité thermique spécifiées.
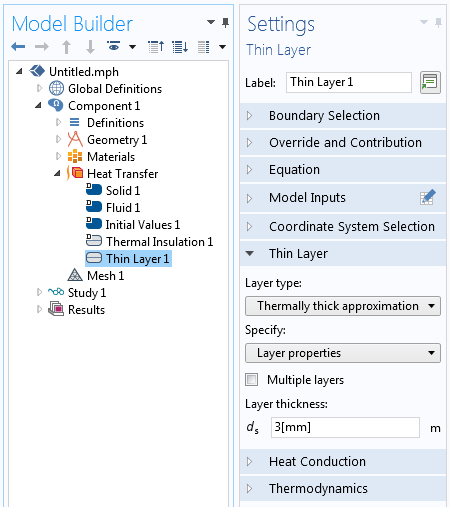
La condition aux limites Couche mince permet de modéliser un mince espace d’air entre deux pièces.
Les deux approches précédentes sont disponibles dans la plateforme de base COMSOL Multiphysics®. Le module Heat Transfer fournit des options supplémentaires pour la condition Couche mince pour prendre en compte des frontières plus générales et multicouches, pouvant être composées de plusieurs couches de matériaux.
Pour conclure sur la modélisation de la convection naturelle et forcée avec COMSOL Multiphysics®
Avant de clore cette discussion, il convient d’aborder rapidement la question du transfert de chaleur par rayonnement. Bien que nous n’ayons pas abordé la question du rayonnement ici, un ingénieur doit toujours en tenir compte. Les surfaces exposées au milieu ambiant rayonnent de la chaleur vers celui-ci et sont chauffées par le Soleil. La puissance du rayonnement solaire est importante – environ 1 000 watts par mètre carré – et ne doit pas être négligée. Pour en savoir plus sur la modélisation du transfert thermique radiatif vers un milieu ambiant, vous pouvez consulter ce précédent billet de blog.
Il y aura également un transfert de chaleur par rayonnement entre les surfaces internes. Le flux de chaleur radiatif entre deux surfaces est une fonction de la différence de température à la puissance 4. Notez que le transfert de chaleur par rayonnement entre deux surfaces à 20°C et 50°C est de 200 watts par mètre carré au maximum, mais qu’il peut atteindre 1 000 watts par mètre carré pour deux surfaces à 20°C et 125°C. Pour évaluer correctement le transfert de chaleur radiatif entre des surfaces, il est en outre important de calculer les facteurs de vue à l’aide du module Heat Transfer.
Aujourd’hui, nous avons examiné plusieurs approches de modélisation de la convection, en commençant par l’approche la plus simple qui consiste à utiliser un coefficient d’échange convectif constant. Nous avons ensuite abordé l’utilisation d’une condition aux limites basée sur une corrélation empirique avant de nous pencher sur l’utilisation d’une conductivité augmentée par convection à l’intérieur d’un domaine et d’une caractéristique de domaine isotherme. Ces approches plus précises ne présentent qu’un coût de calcul légèrement plus élevé. L’approche la plus gourmande en ressources informatiques – le calcul explicite de l’écoulement – est, bien entendu, la plus générale. Nous avons également abordé la question de savoir quand il convient de négliger complètement la convection naturelle et comment procéder dans ce cas. Vous devriez maintenant avoir une meilleure compréhension des options et des compromis disponibles pour la modélisation de la convection naturelle et forcée. Bonne modélisation !
Ressources additionnelles
- Apprenez à modéliser explicitement les écoulements d’air et les transferts de chaleur sur le Blog COMSOL
- Découvrez comment simuler le transfert de chaleur dans ce webinar archivé



Commentaires (0)