
Le lancement de la version 6.2 du logiciel COMSOL Multiphysics® permet d’étendre les capacités de modélisation de la dispersion électrique à l’interface Courants électriques, qui peut être résolue à la fois dans le domaine temporel et dans le domaine fréquentiel. Cette fonctionnalité est particulièrement importante pour modéliser avec précision un large éventail de matériaux, incluant les isolants et les tissus biologiques. Rappelons tout d’abord brièvement ce qu’est la dispersion, puis nous montrerons comment l’inclure dans vos modèles COMSOL et nous expliquerons pourquoi elle est importante.
Contexte
Lorsqu’il s’agit de modéliser des impulsions rapides de courant électrique appliquées à des tissus biologiques, comme dans le contexte de l’ablation cardiaque, de l’électroporation ou de la stimulation neuronale, la nature dispersive du tissu, ainsi que les isolants électriques, doivent être pris en compte.
Tous les matériaux sont électriquement dispersifs, ce qui signifie que leur permittivité relative varie en fonction de la fréquence d’excitation. La permittivité est une mesure de la réaction d’un matériau, ou de sa polarisation, en présence d’un champ électrique. L’ampleur de cette réponse varie avec la fréquence en raison des différents atomes et molécules présents dans le matériau et de leur structure. Il s’agit également d’une mesure de la quantité d’énergie électrique convertie en chaleur, ou perdue, lorsque le matériau est exposé à un signal variant dans le temps. Ces pertes sont dues au mouvement relatif des atomes et des molécules qui oscillent dans les champs variant dans le temps. Lorsque l’on travaille dans le domaine fréquentiel, la permittivité relative est exprimée sous la forme d’un nombre à valeur complexe : \epsilon_r =\epsilon_r^{‘}- i \epsilon_r^{”}, où les parties réelles et imaginaires sont liées par l’intermédiaire des relations de Kramers-Kronig. Deux courbes de dispersion de ce type sont illustrées dans la figure ci-dessous, représentant respectivement un matériau isolant et un tissu biologique. Le premier a une courbe relativement simple, avec des propriétés presque uniformes sur une large bande de fréquences, ce qui montre qu’il n’est pas toujours nécessaire de prendre en compte la dispersion. En revanche, il y aura toujours une bande de fréquence sur laquelle les propriétés varient de manière significative et où il est nécessaire de prendre en compte la dispersion.
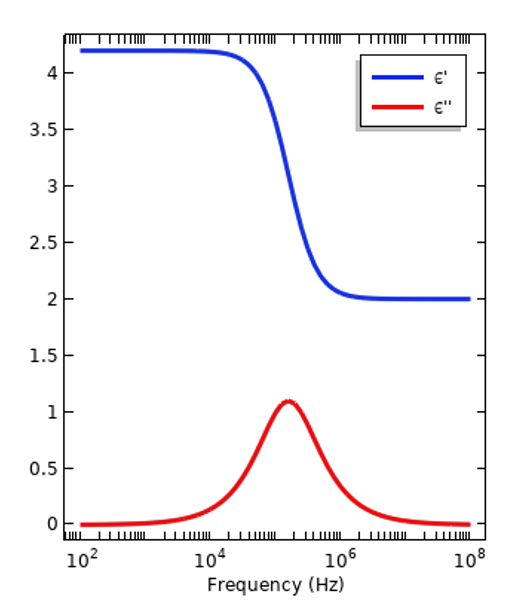
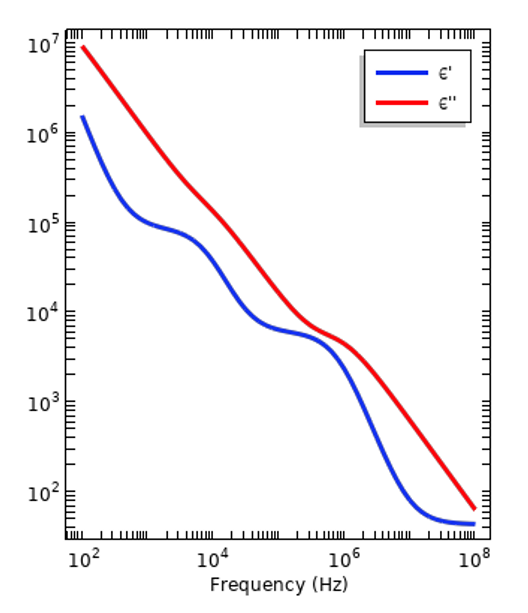
Courbes de dispersion représentatives d’un isolant (à gauche) et d’un tissu humain (à droite). Les amplitudes des parties réelles et imaginaires de la permittivité relative sont représentées.
En complément de ces pertes dépendant de la fréquence, il existe également des pertes électriques dans un champ électrique statique qui sont quantifiées par la conductivité électrique en courant continu, \sigma_{DC}. Tous les matériaux ont une certaine conductivité en courant continu, mais elle peut être très, très faible. Il s’agit d’un mécanisme de perte distinct de la perte dispersive. Il peut être plus pratique d’exprimer toutes les pertes des matériaux, quel que soit le mécanisme, via la conductivité totale : \sigma_{tot} =\sigma_{DC} + 2\pi f \epsilon_0\epsilon_r^{”} ; le graphique ci-dessous illustre ce phénomène pour les deux mêmes matériaux. Il est toutefois important de noter que la conductivité dépendant de la fréquence peut également être présentée sans la composante continue sous la forme suivante : \sigma(f) = 2\pi f \epsilon_0\epsilon_r^{”} avec \sigma_{DC} présenté séparément.
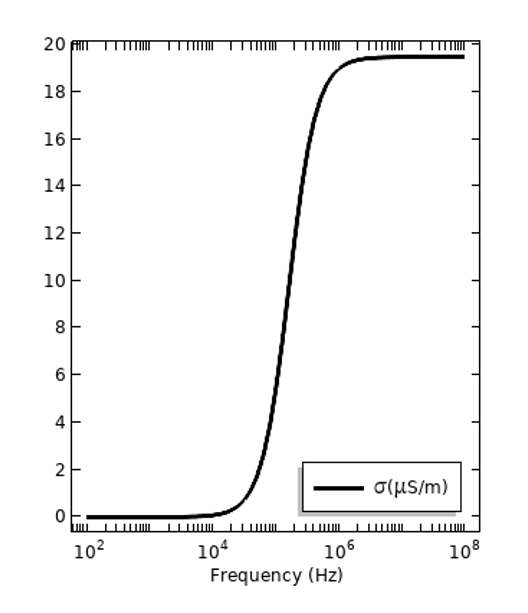
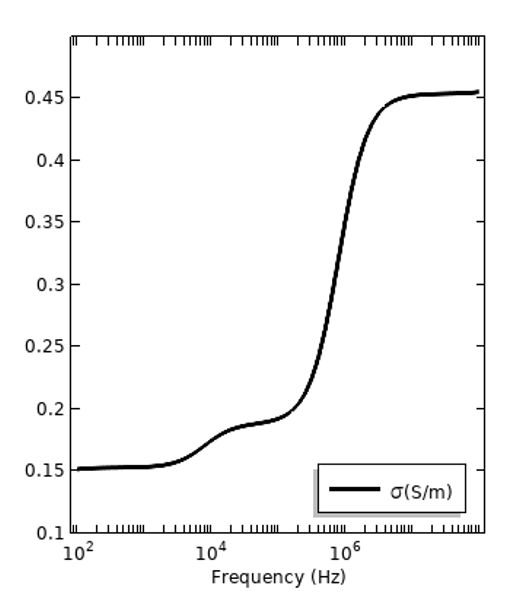
Les pertes des deux mêmes matériaux exprimées sous la forme d’une conductivité électrique totale, la conductivité en courant continu étant présentée en tant que contribution à la perte dispersive.
Bien que les propriétés des matériaux soient déterminées expérimentalement, nous ne voulons pas utiliser directement les données expérimentales car elles comportent une certaine incertitude et ne satisfont pas aux relations de Kramers-Kronig, ce qui conduit à un modèle non causal. À la place, nous ajustons aux données une fonction qui satisfait déjà les relations de Kramers-Kronig et utilisons les coefficients de cette fonction ajustée pour décrire le comportement de notre matériau. Actuellement, le logiciel prend en charge le modèle Debye multipolaire, qui définit alors la permittivité à valeur complexe à partir d’un nombre quelconque, N, de pôles, où chaque pôle, m, a un temps de relaxation, \tau_m, et des contributions de permittivité relative, \Delta \epsilon_r_m :
où \epsilon_\infty est basé soit sur la limite de basse fréquence, \epsilon_\infty \rightarrow \epsilon_{rS}-\Sigma \Delta \epsilon_r_m, soit sur la limite de haute fréquence, \epsilon_\infty \rightarrow \epsilon_{rS}. De plus, les temps de relaxation peuvent éventuellement être décalés en raison d’un changement de température en utilisant l’une des fonctions de changement Vogel-Fulcher, Arrhenius, Williams-Landel-Ferry ou Tool-Narayanaswamy-Moynihan, ou même une fonction définie par l’utilisateur.
Si vous disposez plutôt de données expérimentales pour les parties réelle et imaginaire de la permittivité et que vous souhaitez y ajuster un modèle de Debye, vous pouvez le faire avec la fonctionnalité Ajustement par fractions partielles de la version 6.2 de COMSOL®. Pour en savoir plus sur l’utilisation de cette fonctionnalité, consultez l’article “Fitting the Debye Dispersion Model to Experimental Data” de notre centre d’apprentissage.
Utiliser l’interface Courants électriques
La prise en compte de la dispersion dans un modèle de Courants électriques ne nécessite que quelques étapes. Tout d’abord, une fonctionnalité Conservation du courant doit être ajoutée et appliquée aux domaines concernés. Dans cette fonctionnalité, le Type de matériau doit être réglé sur Solide. Cela permet tout de même de modéliser un fluide, en supposant qu’il ne se déforme pas.
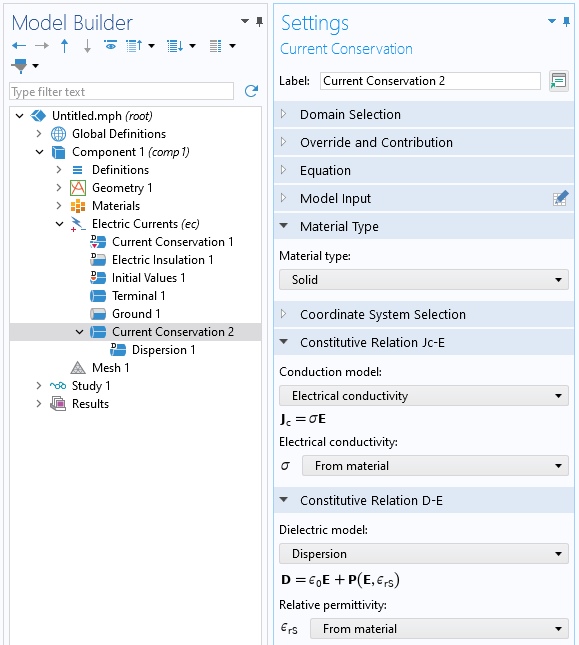
La fonctionnalité Conservation du courant, où le modèle de dispersion Diélectrique peut être sélectionné.
Après avoir sélectionné Dispersion pour l’option Modèle diélectrique, un sous-nœud supplémentaire apparaît. Dans les réglages de cette fonctionnalité, il est possible de renseigner les branches du modèle Debye multipolaire ainsi que le comportement limite, comme le montre la capture d’écran ci-dessous. Au lieu de saisir les pôles ou les branches, il est également possible de spécifier les données de relaxation via le modèle Facteur de perte tangent constant, qui nécessite comme données d’entrée un facteur de perte tangent, une fréquence centrale et une bande passante. À partir de ces données, le logiciel détermine automatiquement le nombre de pôles, les temps de relaxation et les contributions à la permittivité relative. Il est également possible d’utiliser le modèle plus simple de Debye, avec un seul pôle. Les effets thermiques qui entraînent un décalage des temps de relaxation peuvent être activés de façon optionnelle à l’aide des réglages Effets thermiques.
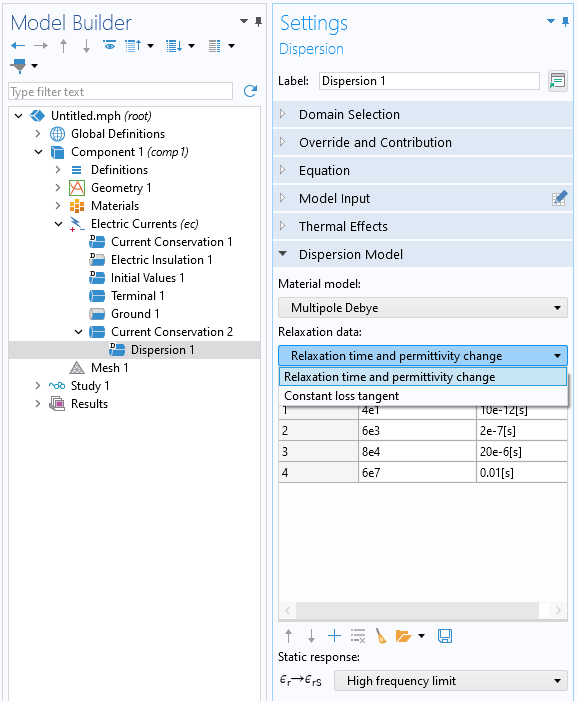
Le sous-nœud Dispersion, dans lequel sont renseignées les branches du modèle Debye multipolaire et où le comportement limite est spécifié.
Analyse des résultats
Nous pouvons examiner comment la dispersion affecte la réponse d’un système simple, tel qu’un condensateur à plaques parallèles fonctionnant dans le domaine fréquentiel, et essayer nos deux matériaux différents pris en sandwich à l’intérieur. Les graphiques ci-dessous montrent comment les parties réelles et imaginaires de l’impédance varient en fonction de la fréquence.
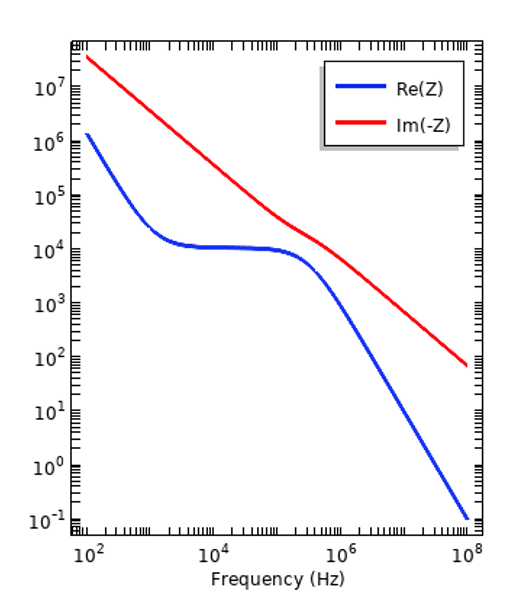
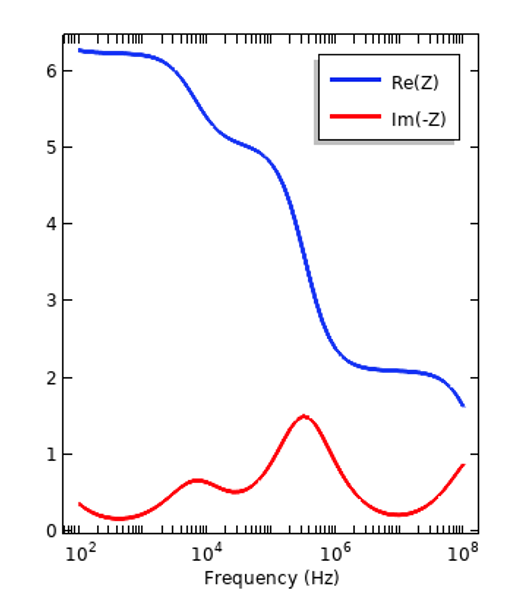
Impédance d’un condensateur à plaques parallèles avec un échantillon d’isolant (à gauche) et de tissu (à droite) placé à l’intérieur. Notez que la partie imaginaire négative de l’impédance est tracée.
Nous pouvons également utiliser le même modèle pour examiner les résultats d’une excitation du même système dans le domaine temporel. Nous nous intéresserons uniquement à l’échantillon de tissu, car la variation de la réponse en fonction de la fréquence est plus importante. La configuration du matériau dispersif est la même, mais il est utile de passer en revue les différentes façons d’exciter un tel système. Nous commençons par exciter le système en appliquant un courant avec un échelon lissé passant de 0 à 1 A sur 10 ns, et nous calculons la réponse sur 100 µs en traçant la tension détectée au terminal (voir la figure ci-dessous). Les résultats sont tracés en fonction du temps et en fonction du temps en échelle logarithmique.
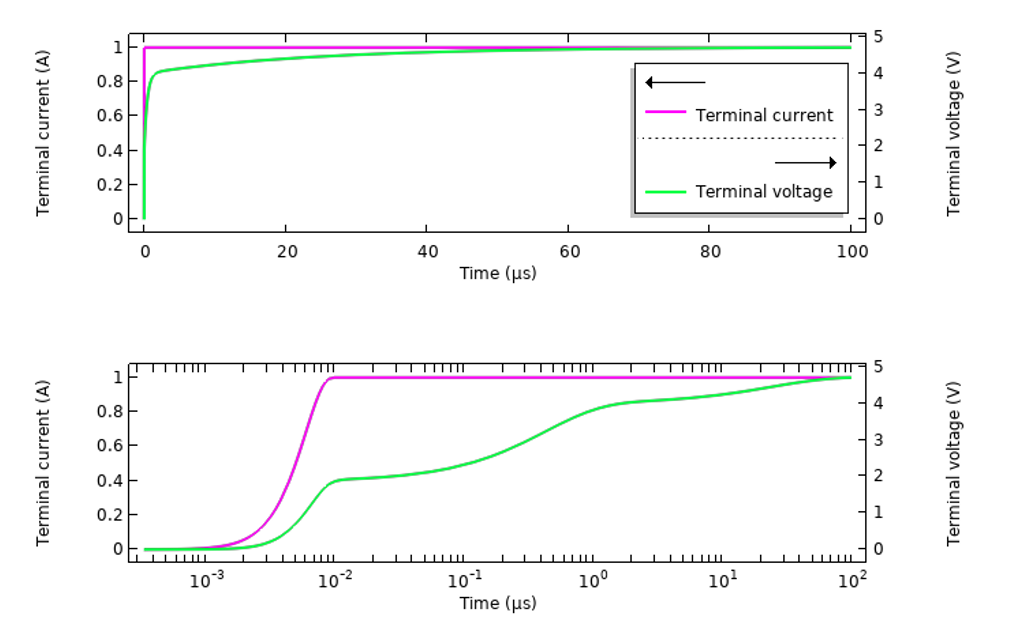
Réponse transitoire de l’échantillon de tissu à un courant imposé en fonction du temps.
Il est intéressant de comparer ces résultats à ceux d’un modèle excité par un signal de tension en échelon lissé similaire se propageant le long d’une ligne de transmission. Les figures ci-dessous montrent la réponse en termes de courant et de tension mesurés. Il convient de noter que le signal de tension représenté ici est la somme du signal de tension en échelon lissé incident et du signal réfléchi par la structure et le matériau. Ce signal total présente un comportement variable dans le temps en raison de la dispersion du matériau.
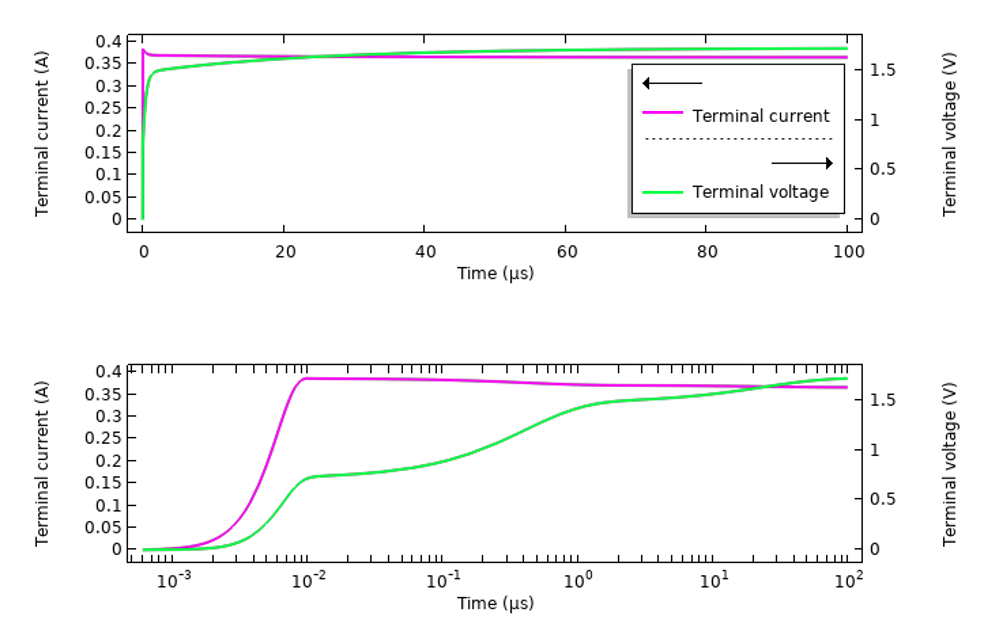
La réponse transitoire de l’échantillon de tissu excité par une ligne de transmission, avec un signal de tension en échelon.
Conclusion
Il est désormais possible et simple de modéliser la dispersion électrique dans l’interface Courants électriques. Cette loi de comportement permet une représentation plus précise de la réponse électrique réelle ainsi que des pertes dans les modèles en domaine fréquentiel et en domaine temporel. Cette fonctionnalité est utile pour la modélisation de nombreux matériaux.
Il convient de noter que la modélisation de la dispersion électrique est également possible via l’interface Electrostatique, et ce depuis la version 6.0, dans laquelle elle est principalement destinée à la modélisation de matériaux piézoélectriques à pertes. De plus, si la modélisation se fait à des fréquences beaucoup plus élevées, le module RF et le module Wave Optics proposent d’autres modèles de dispersion.







Commentaires (0)