Comment positionner les conditions aux limites d’entrée et sortie dans des simulations CFD

Lorsque l’on met en place des simulations d’écoulement fluide, on se concentre généralement sur un unique composant (ou éventuellement quelques uns) d’un système plus grand, par exemple une pompe ou un réservoir de sédimentation dans une usine de traitement des eaux. Naturellement, cela soulève une question: À quelle distance peut-on appliquer des conditions limites sans interférer avec le processus ? Dans cet article de blog, nous examinons les effets de proximité des limites d’entrée et de sortie pour les écoulements internes et externes d’un fluide homogène avec une compressibilité négligeable.

Positionner des conditions d’entrée et de sortie pour des écoulements internes

Les simulations CFD sont généralement coûteuses en termes de ressources de calcul et nous essayons naturellement de minimiser le nombre de degrés de liberté dans nos simulations. Si nous poussions la démarche à l’extrême, nous pourrions nous retrouver avec une géométrie dans laquelle une frontière d’entrée et une frontière de sortie se rejoignent. Imaginons un coude à 90° dans un tuyau à section semi-circulaire.

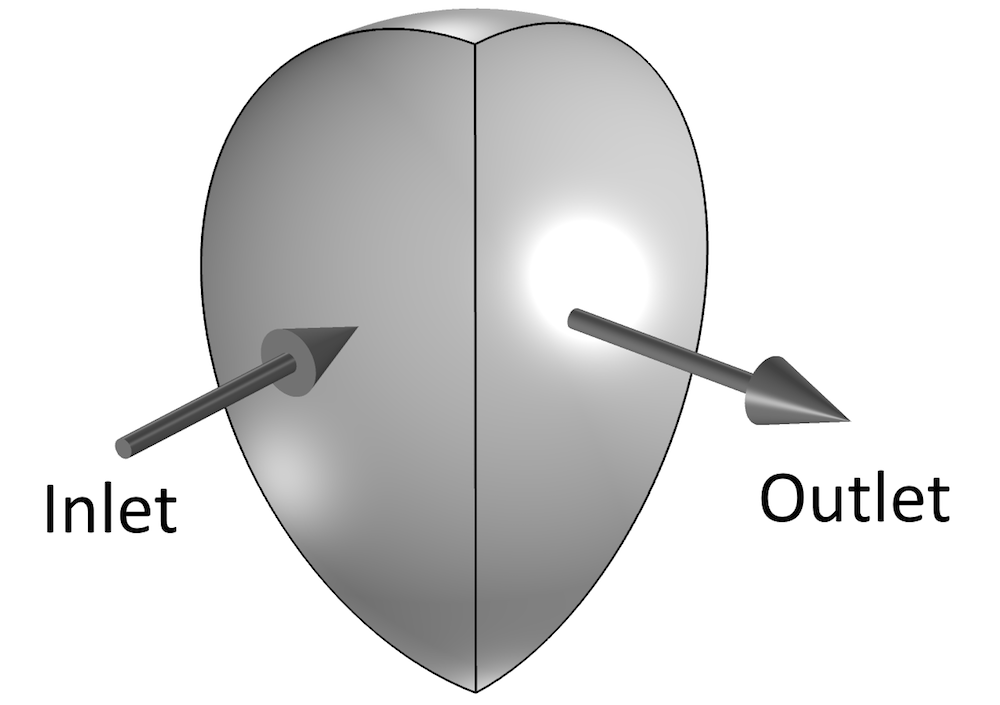
Une conduite de section semi-circulaire avec un coude à 90°.

Si la simulation est configurée selon la géométrie illustrée ci-dessus, les frontières d’entrée et de sortie partagent une arête. Dans de nombreux cas, cette situation peut à elle seule entraîner de sérieux problèmes de convergence. Cependant, dans ce cas particulier, la solution converge en quelques itérations. Considérons également une simulation correctement configurée avec des canaux d’entrée et de sortie étendus à une longueur de 10 rayons (voir ci-dessous).

Un coude à 90° avec des canaux d’entrée et de sortie prolongés.

Les simulations sont réalisées pour un nombre de Reynolds de 120, basé sur le diamètre hydraulique, D_{h}=4A/P, où A est l’aire de la section et P son périmètre. Un profil de vitesse uniforme est appliqué aux entrées et une contrainte normale nulle est appliquée aux sorties. L’image ci-dessous montre la pression au niveau du coude pour les deux simulations, avec des canaux d’entrée et de sortie prolongés à gauche, et sans ces canaux à droite. Pour le cas des canaux d’entrée et de sortie prolongés, la pression moyenne sur la frontière aval est soustraite de la pression afin que les deux résultats aient une pression moyenne nulle sur cette frontière.

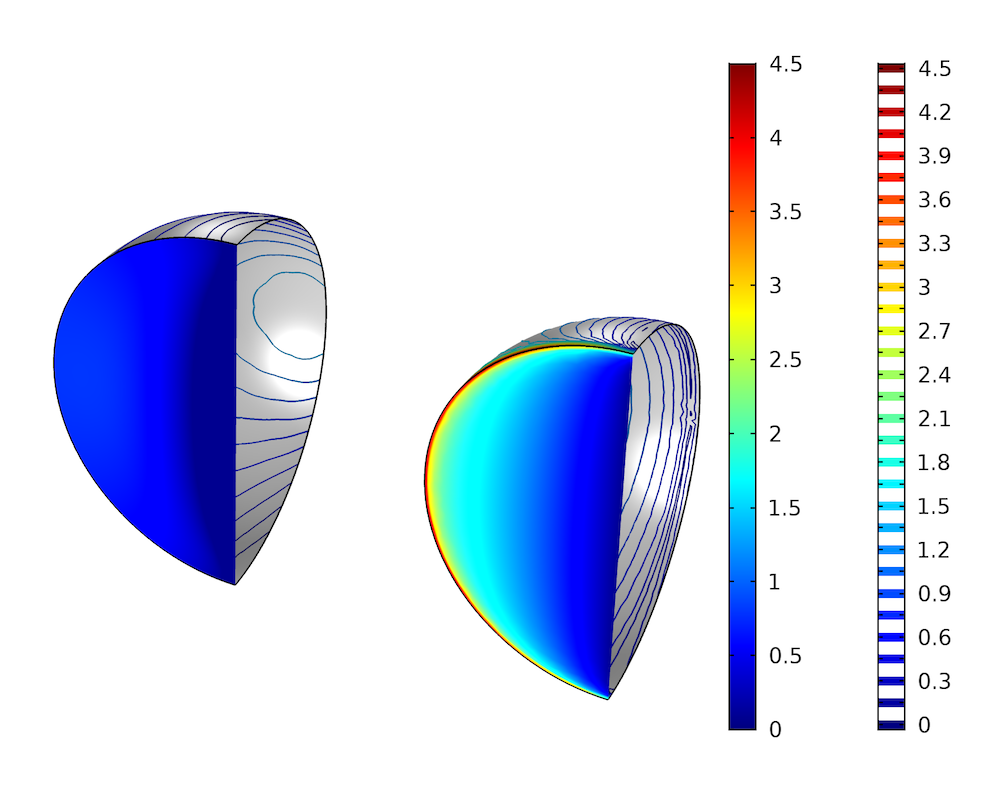
Variations de pression à travers un coude à 90° dans une conduite de section semi-circulaire, avec une représentation de la pression sur les surfaces correspondant à l’écoulement amont et des ligne d’isopressions au niveau des parois du coude. Le graphique de gauche montre les résultats avec des canaux d’entrée et de sortie prolongés, et le graphique de droite montre les résultats sans ces canaux.

Les résultats de simulation sans canaux d’entrée et de sortie prolongés montrent une variation de pression plus grande. Il y a un fort gradient de pression au niveau de la paroi proche de l’entrée, dû à l’incompatibilité entre le profil de vitesse uniforme appliqué et la condition aux limites de Non glissement à la paroi. Le graphique de gauche présente une pression beaucoup plus uniforme du côté amont du coude, ce qui indique que l’écoulement est entièrement développé lorsqu’il atteint le coude. La pression n’est cependant pas totalement uniforme: elle semble légèrement plus faible au niveau de l’angle vif. Cela indique une influence en amont du coude. On observe également un point de stagnation sur la paroi du canal à l’opposé de la frontière amont. Le coefficient de pertes à travers le coude, défini comme suit

(1)

est de 2.3 sans les canaux d’entrée et de sortie prolongés, et de 0.6 avec ceux-ci. On peut obtenir plus d’informations en examinant le champ de vitesse.

Profils de vitesse et lignes de courant dans un coude à 90° d’une conduite de section semi-circulaire.

La figure ci-dessus montre le profil de vitesse en quatre positions en amont du coude, quatre positions en aval du coude ainsi que les lignes de courant dans le plan médian. En amont, nous pouvons voir comment le profil de vitesse uniforme évolue vers un profil entièrement développé. Au niveau du coude, nous détectons le point de stagnation sur la paroi de la conduite, faisant face au canal d’entrée, ainsi que la zone de recirculation associée. En aval du coude, il y a une autre zone de recirculation, et nous pouvons voir que le profil entièrement développé est obtenu uniquement à l’extrémité du canal de sortie. Tout ceci est absent dans la géométrie simple (contenant seulement le coude à 90°), et il n’est pas surprenant que nous obtenions une perte de charge erronée.

L’option Ecoulement entièrement développé dans les conditions aux limites d’Entrée et de Sortie permettent d’éviter la présence de canaux d’entrée et de sortie excessivement longs. Les résultats des deux figures précédentes indiquent clairement que nous devrions appliquer ces conditions à une certaine distance du coude pour obtenir de bons résultats. Mais à quelle distance en amont et aval devons nous appliquer cette option d’Ecoulement entièrement développé? Si nous prolongeons les canaux d’entrée et de sortie de chacun 1 rayon à partir du coude, le coefficient de perte de charge résultant à travers le coude est de 0.54, alors qu’à 2 rayons dans chaque direction ce coefficient devient 0.58. A partir de là, la convergence vers la valeur de 0.60 devient plus lente. De fait, dans ce cas, 2 rayons dans chaque direction semble un bon compromis.

Au fur et à mesure que le nombre de Reynolds augmente, la zone de recirculation en aval du coude a une longueur de plus en plus grande et finit par devenir instable. Pour un nombre de Reynolds de 1200, le coefficient de perte ne change plus significativement lorsque le canal de sortie est prolongé de 20 rayons, dès lors que l’option Ecoulement entièrement développé est appliquée à l’extrémité du canal. D’après des corrélations pour les longueurs d’entrée dans les conduites,

(2)

pour un écoulement laminaire, et

(3)

pour un écoulement turbulent, nous pouvons estimer à quelle distance en aval du canal le profil entièrement développé est obtenu. Notez que la longueur d’entrée de l’écoulement turbulent est généralement plus courte que celle de l’écoulement laminaire à nombre de Reynolds élevé. Il faut atteindre des nombres de Reynolds d’ordre O(10^8) pour que les longueurs d’entrée soient de l’ordre de O(10^2) diamètres hydrauliques .

Pour les deux cas laminaires avec des nombres de Reynolds de 120 et 1200, les longueurs d’entrées obtenues à partir de (2) sont d’environ 7.5 et 75 rayons, respectivement. En utilisant l’option Ecoulement entièrement développé au niveau des sorties, nous obtenons de bons résultats avec des canaux de sortie mensurant environ 1/3 de ces longueurs.

Quant à l’influence de l’écoulement amont, elle devrait diminuer avec l’augmentation du nombre de Reynolds, car la nature elliptique de l’équation de Navier-Stokes diminue avec l’augmentation du nombre de Reynolds. Nous pouvons estimer la région d’influence amont en examinant l’écoulement potentiel dans une géométrie similaire.

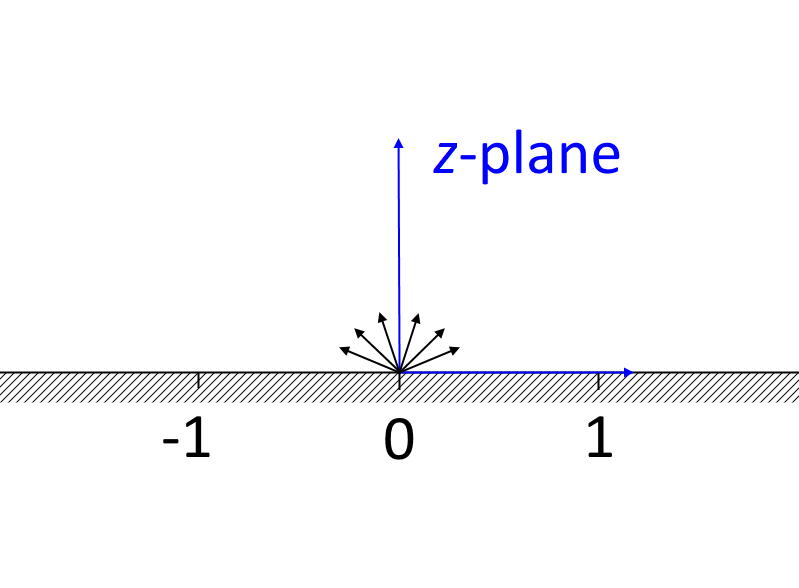
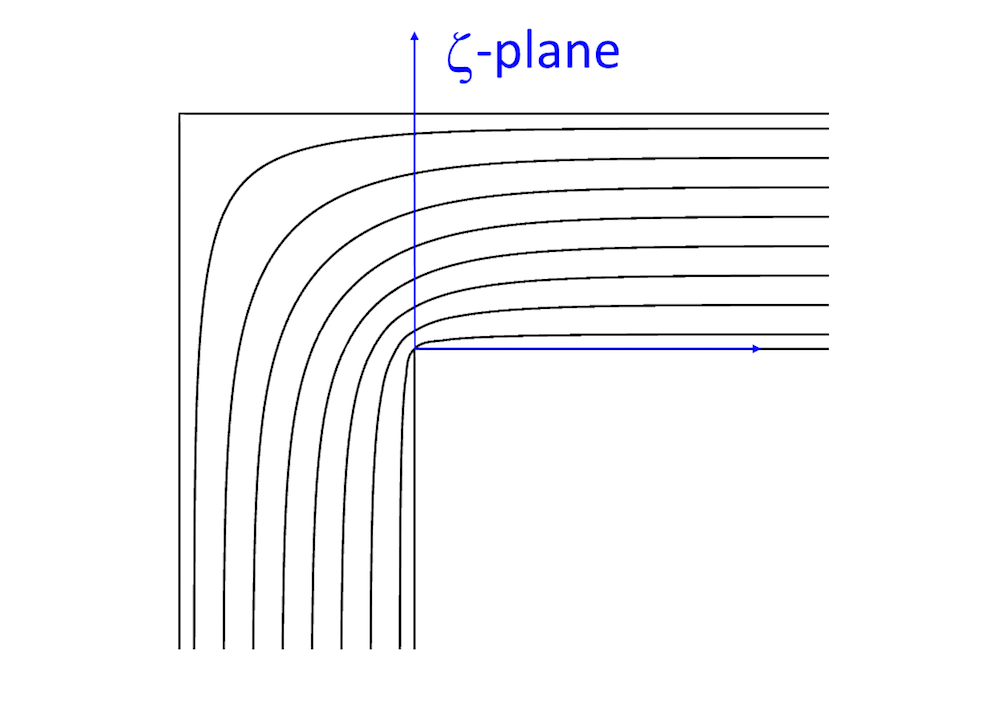
Représentation du demi-plan supérieur d’un coude à 90° en utilisant la transformation de Schwarz-Christoffel.

En utilisant la transformation de Schwarz-Christoffel (Ref. 1), le demi-plan supérieur du plan complexe z peut être mappé sur un angle à 90° dans le plan complexe \zeta. L’entrée, positionnée en -i\infty dans le plan \zeta, correspond à une source à l’origine dans le plan z, tandis que la sortie est positionnée en \infty dans les deux plans. Les coins extérieurs et intérieurs du coude dans le plan \zeta correspondent respectivement aux points -1 dans le plan z. Le champ de vitesse dans le plan \zeta est obtenu sous forme implicite comme

(4)

L’image ci-dessous montre le coefficient de pression le long de la paroi interne en fonction de la distance adimensionnée en amont du coude pour la solution de l’écoulement potentiel.

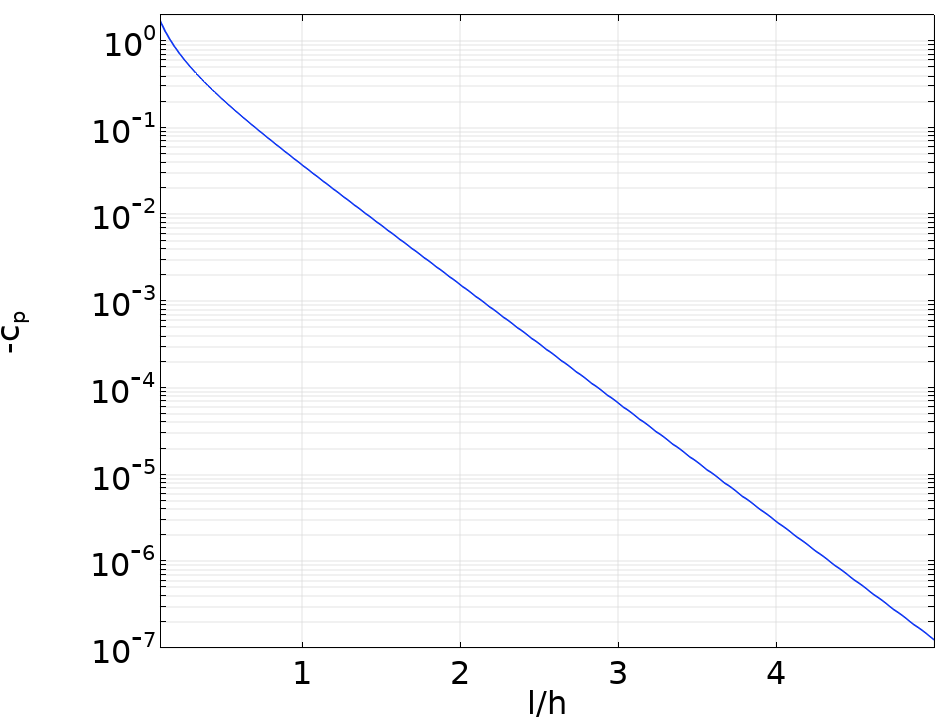
Le coefficient de pression le long de la paroi interne en amont d’un coude à 90°.

Dans la figure, le coefficient de pression est basé sur la différence entre la pression locale et la pression éloignée en amont et h est la largeur du canal. On observe que le coefficient de pression est d’ordre O(10^{-3}) lorsque la distance amont du coude est de deux largeurs de canal. Par conséquent, à condition d’utiliser l’option Ecoulement entièrement développé à l’entrée, il suffit de prolonger notre conduite (ou canal) d’entrée de quelques diamètres hydrauliques en amont.

Prise en compte de la gravité

L’option Ecoulement entièrement développé dans les conditions aux limites d’Entrée et de Sortie sont disponibles avec l’option complémentaire Compenser la pression hydrostatique (écoulement incompressible) ou l’option Compenser pour l’approximation de pression hydrostatique (écoulement faiblement compressible ou écoulement compressible) lorsque la gravité est active dans le modèle. Cette option supplémentaire donne le profil de pression hydrostatique exact sur la frontière pour un écoulement incompressible et une bonne approximation pour un écoulement faiblement compressible et un écoulement compressible. Des précautions supplémentaires doivent être prises lorsque le fluide à la frontière d’entrée ou de sortie est fortement stratifié, comme dans le cas d’un écoulement multiphasique. Dans ces cas, il peut être utile d’ajouter un déversoir dans lequel l’écoulement est rendu parallèle au vecteur gravité.

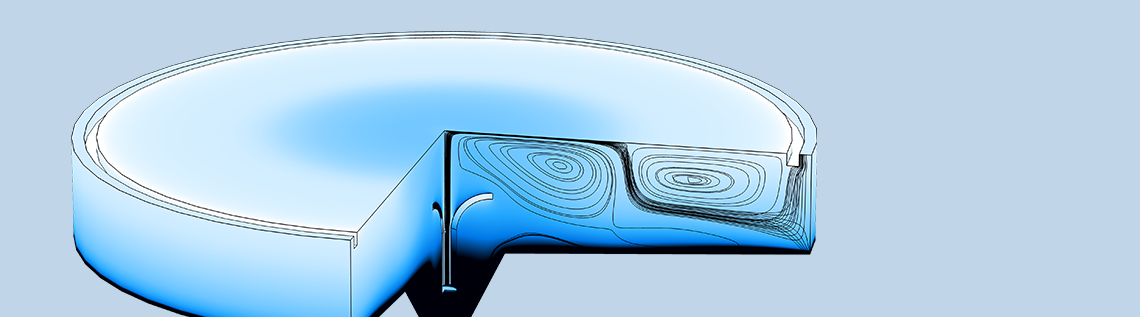
Des problèmes peuvent également survenir lorsque l’on travaille à l’encontre de la gravité. L’image ci-dessous montre un grand bassin de sédimentation avec un long temps de séjour, permettant à la phase en suspension (lourde) de se déposer et de sortir par la sortie inférieure. La phase légère sort verticalement par une sortie annulaire située à proximité du bord extérieur. Les lignes de courant grises correspondent au champ de vitesse de la phase légère, tandis que les lignes de courant noires correspondent au champ de vitesse de la phase lourde. Une petite partie de la phase lourde sort par la sortie de la phase légère. Ici, la phase lourde s’écoule dans la direction opposée à la gravité, ce qui entraîne la formation d’un petit tourbillon à côté du bord extérieur, car certaines des particules en suspension retombent. Ce petit tourbillon peut avoir un impact négatif sur le pas de temps du solveur, entraînant un temps de calcul total plus long. Une solution pourrait être d’ajouter un déversoir, permettant au flux de sortir dans la direction de la gravité.

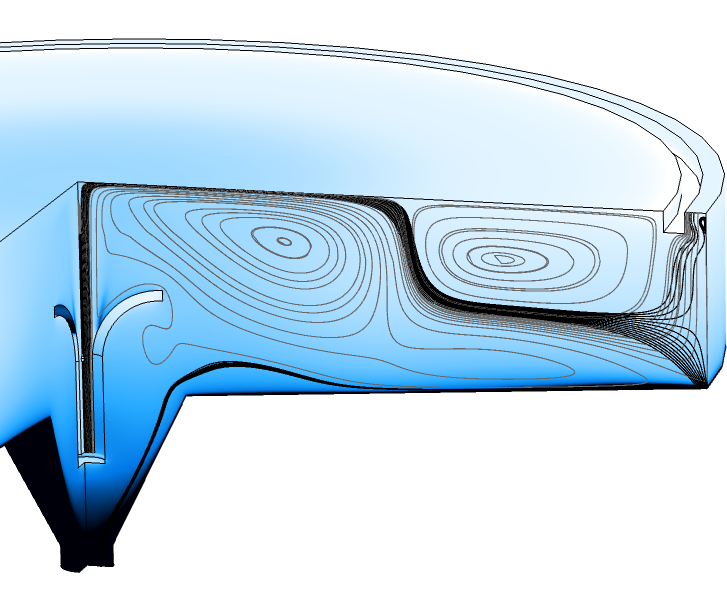
Fraction volumique de la phase dispersée ( en couleur ) et lignes de courant, en gris pour la phase légère et en noir pour la phase lourde, dans une cuve de sédimentation.

Un autre exemple de cas où les frontières d’entrée et de sortie se croisent se présente lors de la simulation d’un panache thermique, illustré ci-dessous. Dans ce cas, ce n’est pas une condition aux limites d’Entrée qui est imposée au niveau de la frontière d’entrée (La surface cylindrique de la figure). A la place, une fonctionnalité de Frontière ouverte est appliquée. Dans les deux fonctionnalités Frontière ouverte et Sortie (frontière supérieure), l’option Compenser pour l’approximation de la pression hydrostatique est appliquée. C’est essentiel puisque la pression induite par la flottabilité dans le modèle est de trois ordres de grandeur inférieure à la pression hydrostatique. Une autre option, elle aussi essentielle, est l’option Suppression de reflux dans la condition de Sortie.

Panache thermique turbulent, montrant l’amplitude de la vitesse (en couleur) et les isovaleurs des écarts de pression par rapport aux conditions hydrostatiques.

Les petites perturbations des isovaleurs à la frontière supérieure sont dues à une incompatibilité avec une pression constante. Elles peuvent être éliminées en utilisant l’option Approximation de Boussinesq dans le noeud de couplage multiphysique Ecoulement non-isotherme.

Positionner les conditions d’entrée et de sortie pour les écoulements externes

Dans les applications d’écoulement externe, comme l’écoulement autour de véhicules et de bâtiments, les conditions loin de l’obstacle sont généralement fixées à un vecteur vitesse constant sur les frontières d’entrée et à une pression constante sur les frontières de sortie. La question de savoir dans quelle mesure la distance de l’obstacle à laquelle ces conditions sont appliquées influence la solution se pose à nouveau. Pour un écoulement externe, il s’avère que cette distance varie avec les dimensions spatiales du modèle. Pour les modèles 2D, la distance requise est d’un ordre de grandeur plus grand que pour les modèles 3D et 2D axisymétriques. Une fois de plus, nous pouvons examiner les solutions d’écoulement potentiel idéal pour essayer d’en comprendre la raison.

Pour un écoulement externe autour d’un obstacle, la vorticité est créée dans les couches limites de la surface solide. Les couches limites sur les différents côtés de l’obstacle peuvent fusionner au niveau du bord de fuite, formant une fine nappe de vorticité qui est advectée en aval dans un sillage. Si la couche limite d’un côté se sépare de l’obstacle en raison d’une instabilité ou de l’existence d’un angle convexe vif, le sillage sera plus large. Dans les deux cas, la vorticité qui est transférée en aval est confinée dans le sillage et l’écoulement à l’extérieur du sillage est quasiment irrotationnel.

Ecoulement turbulent autour d’un profil d’aile NACA. La couche limite sur la partie supérieure du profil se sépare en amont du bord de fuite.

L’obstacle et son sillage déplacent les lignes de courant de l’écoulement libre, et nous pouvons considérer l’écoulement à de grandes distances de l’obstacle comme étant la somme d’un écoulement uniforme et d’une source.

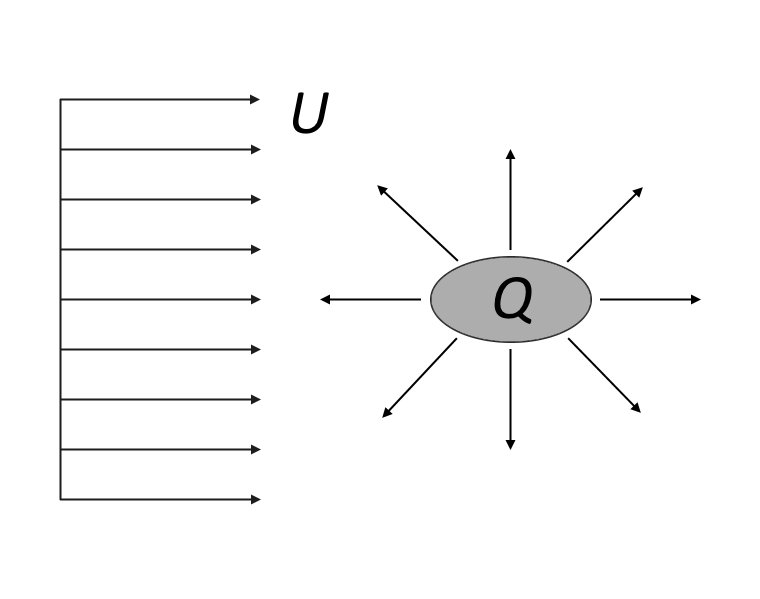
Ecoulement potentiel à une grande distance d’un obstacle et de son sillage.

Les champs de vitesse résultants en 2D et 3D peuvent être exprimés comme suit

(5)

où R=\sqrt{x^{2}+y^{2}}, r=\sqrt{x^2+y^2+z^2}, la source est positionnée à l’origine, et l’écoulement libre est orienté selon la direction des x positifs.

L’intensité de la source peut, dans les deux cas, être liée aux dimensions de l’obstacle. A la position xde la source, le déplacement des lignes de courant est de y_{0}=Q/(4U) dans le cas 2D et de r_{0}=\sqrt{Q/(2\pi U)} dans le cas 3D. Les valeurs limites situées loin en aval sont y_{\infty}=Q/(2U) et r_\infty=\sqrt{Q/(\pi U)}, respectivement. Pour les besoins de l’exemple, les valeurs représentatives de la taille de l’obstacle de 2y_{0} ou 2y_\infty en 2D et 2r_{0} ou 2r_\infty en 3D. Nous utilisons ici d=Q/(2U) en 2D et d=\sqrt{2Q/(\pi U)} en 3D. Nous pouvons tirer de l’équation de Bernoulli une estimation du coefficient de pression à de grandes distances

(6)

En introduisant les champs de vitesse de l’écoulement potentiel ainsi que les estimations des intensités des sources, on trouve

(7)

Le coefficient de pression diminue donc selon d/R en 2D et (d/r)^2 en 3D. Pour réduire l’influence des conditions aux limites des frontières externes à environ O(10^{-2}), nous devons positionner les frontières externes du domaine de calcul à une distance de l’ordre de la taille de 100 obstacles en 2D, et 10 obstacles en 3D.

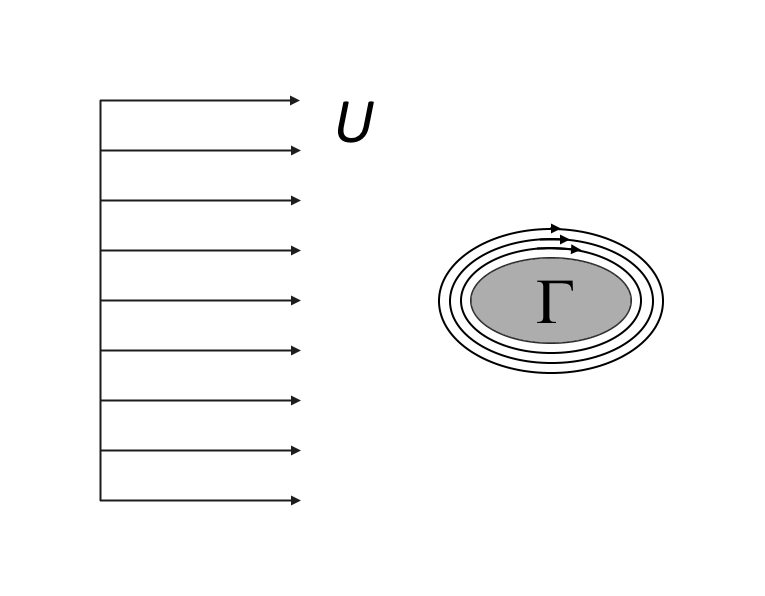
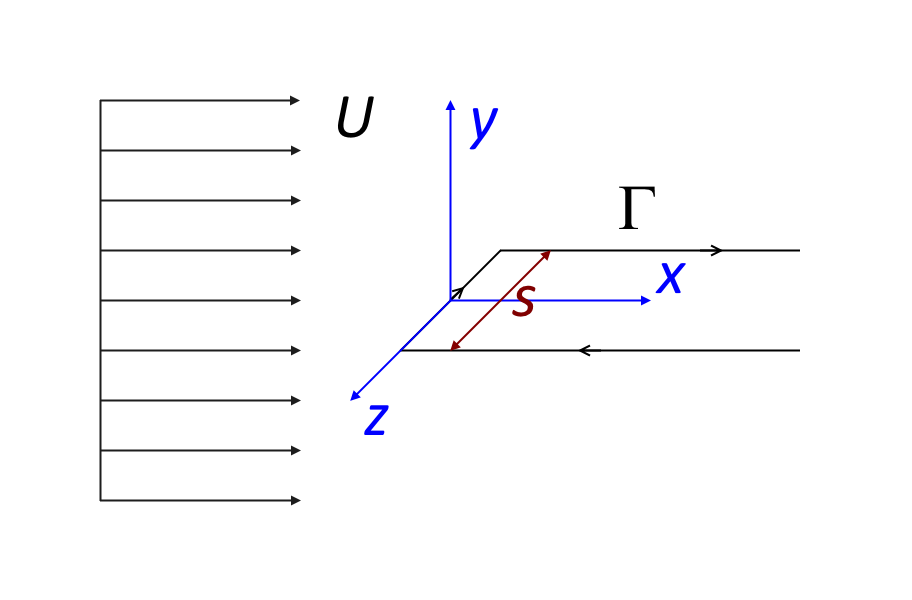
Selon la forme et l’orientation de l’obstacle, le décollement tourbillonnaire peut induire une circulation qui génère des forces latérales (portance). L’écoulement potentiel à grande distance de l’obstacle peut être approximé par un écoulement uniforme et un tourbillon ponctuel en 2D ou un écoulement uniforme et un tourbillon linéaire en forme de fer à cheval en 3D.

Ecoulement potentiel autour d’un obstacle avec circulation (portance). En 2D (gauche), l’écoulement potentiel est constitué d’un écoulement uniforme dans la direction x et un tourbillon ponctuel situé à l’origine. En 3D (droite), l’écoulement potentiel est composé d’un écoulement uniforme dans la direction x et d’un tourbillon linéaire en forme de fer à cheval dont la portée s est dans la direction z et étendu à l’infini dans la direction x .

A de grandes distances de l’obstacle, les champs de vitesse de l’écoulement potentiel correspondant à la figure ci-dessus sont donnés par

(8)

Notez que la solution 2D est obtenue à partir de la solution 3D en fixant z à zéro et en laissant s\rightarrow\infty. La circulation peut, dans la plupart des cas envisageables, être reliée à la vitesse de l’écoulement libre et à la dimension de l’obstacle dans le sens de l’écoulement (corde), c , par

(9)

où \alpha est l’angle d’attaque et-\beta est l’angle de “portance nulle” (tous deux en radians).

Cette dernière résulte de la forme (courbure) de l’obstacle ; une cambrure de profil d’aile, par exemple. En introduisant les solutions de l’écoulement potentiel asymptotique et l’expression pour \Gamma dans la définition du coefficient de pression, on obtient

(10)

L’angle de déflexion total, \alpha+\beta, doit être au moins d’un ordre de grandeur plus petit que l’unité pour que l’estimation de \Gamma soit valide. Pour une sphère, les dimensions d, c, et s sont égales. Les règles sur la proximité des limites extérieures imposées par la circulation sont donc moins contraignantes que celles imposées par la source.

Pour un profil d’aile, les trois dimensions ont toutes des ordres de grandeur différents s\sim 10c\sim 100d. En 2D, les restrictions imposées par le tourbillon ponctuel sont d’une importance équivalente à celles imposées par la source, étant donné que d\sim c(\alpha+\beta). Si un profil d’aile 3D seul devait être modélisé, les règles imposées par le vortex linéaire aurait une importance d’ordre 100 fois supérieure à celles imposées par la source. Souvent, le profil d’aile est connecté au fuselage avec d\sim c, auquel cas les deux restrictions revêtent une importance similaire en 3D. L’image ci-dessous montre une simulation 2D d’un écoulement autour d’un Profil d’aile NACA 0012 avec un angle d’attaque de 14°. Pour minimiser l’influence des conditions aux limites externes, le domaine est étendu à 100 longueurs de corde dans chaque direction. La longueur caractéristique pertinente ici est relevant c\alpha, puisque \beta=0 pour un profil symétrique. Selon les estimations ci-dessus, il en résulte des coefficients de pression de quelques dixièmes de pourcent.

Simulation 2D d’un profil d’aile NACA 0012 avec un angle d’attaque de 14°.

La figure ci-dessous montre une simulation 3D d’un avion en décrochage avec un angle d’attaque de 20°. Le domaine de calcul est défini par une demi-sphère d’un rayon de 15 m et un cylindre d’une hauteur de 30 m. L’envergure de l’aile est d’environ 18 m, le diamètre du fuselage est de 2,4 m et la corde maximale multipliée par l’angle d’attaque est d’environ 1,3 m. En introduisant ces chiffres, on obtient des coefficients de pression de quelques pourcents, ce qui est un peu élevé. Par conséquent, les résultats de cette simulation seraient probablement meilleurs si le domaine était étendu plus loin de l’avion.

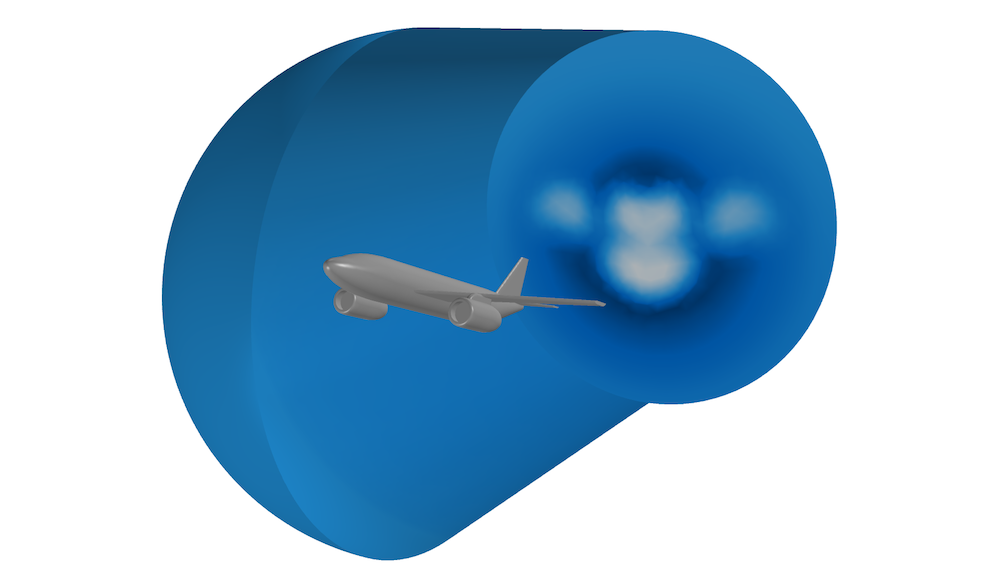
Domaine de calcul, dont la couleur représente l’amplitude de la vitesse, pour la simulation d’un avion en décrochage.

Conclusions sur le positionnement des conditions d’entrée et de sortie

Dans cet article de blog, nous avons montré l’utilisation de la théorie des écoulements potentiels et des corrélations empiriques pour déterminer les positions appropriées des frontières d’entrée et de sortie. Pour les écoulements internes, nous avons utilisé des corrélations empiriques pour écoulement laminaire et turbulent afin de déterminer la longueur de conduite nécessaire pour obtenir un écoulement entièrement développé. L’extension du domaine en amont et en aval en ce sens a clairement permis d’obtenir des simulations d’écoulement précises. Toutefois, cette longueur augmente avec le nombre de Reynolds et peut, surtout pour les écoulements laminaires à nombre de Reynolds élevé, devenir trop importante. L’utilisation des options Ecoulement entièrement développé dans les conditions aux limites d’Entrée et de Sortie réduit de façon considérable cette longueur. Dans la partie aval, une réduction de la longueur par trois semble être un compromis satisfaisant entre précision et coût en termes de ressources de calcul. L’utilisation de la théorie de l’écoulement potentiel montre qu’il n’est pas nécessaire que la distance amont soit supérieure à quelques diamètres hydrauliques. L’option Ecoulement entièrement développé prend également en compte la gravité lorsqu’elle est active. Des problèmes peuvent encore survenir lorsque l’écoulement est fortement stratifié, comme dans le cas d’un écoulement multiphasique. Dans ce cas, il est conseillé de rediriger la sortie dans le sens de la gravité.

En ce qui concerne les écoulements externes, la théorie des écoulements potentiels a été utilisée pour estimer la distance à laquelle les variations de pression induites par l’écoulement autour d’un obstacle deviennent négligeables. Il a été déterminé que la pression varie selon \sim D/R en 2D et selon \sim A/R^2 en 3D et 2D axisymétrique, où R est la distance au centre de l’obstacle tandis que D et A sont respectivement la longueur et l’aire de l’obstacle en projection sur un plan orthogonal à l’écoulement libre.

Avec un peu de chance, ces estimations vous serviront lorsque vous implémenterez vos propres simulations. Pensez néanmoins à vérifier vos résultats. Lorsqu’on utilise l’option Ecoulement entièrement développé pour un écoulement interne, le moyen le plus simple est de faire varier la longueur des canaux d’entrée et de sortie et de regarder si les résultats changent. Pour un écoulement externe, vérifiez si la vitesse ne s’écarte pas plus que la tolérance autorisée des valeurs du champ de vitesse de l’écoulement libre au niveau des frontières en pression, à l’exception du sillage, et de façon similaire pour la pression sur les frontières spécifiées en vitesse.

Référence

1. R.V. Churchill & J.W. Brown, Complex Variables and Applications, 5^th ed., McGraw-Hill, 1990.

Note de l’éditeur: Ce blog a été mis à jour le 25/04/2023 pour refléter le fait que l’option Ecoulement entièrement développé est incluse dans la plateforme COMSOL Multiphysics^®.