Admettons que vous travaillez sur un cas de modélisation dans lequel les chargements se déplacent, traversant différents éléments de maillage et différentes frontières au cours de la simulation. Dans ce cas, vous pourriez vouloir appliquer une condition aux limites seulement à une partie de la frontière géométrique ou uniquement sous certaines conditions. Dans cet article de blog, nous allons voir comment vous pouvez utiliser la flexibilité de COMSOL Multiphysics® pour gérer ce type de situation.
Catégoriser les conditions aux limites
Dans le traitement mathématique des équations aux dérivées partielles, vous rencontrerez des conditions aux limites de type Dirichlet, Neumann, et Robin. Avec une condition de Dirichlet, vous imposez la valeur de la variable que vous résolvez. Une condition de Neumann est utilisée pour imposer un flux, c’est à dire le gradient de la variable dépendante. Une condition de Robin est hybride entre les deux types de conditions aux limites précédentes, dans laquelle on impose une relation entre la variable et son gradient.
Le tableau suivant propose des exemples provenant de divers domaines de la physique qui montrent l’interprétation physique correspondante.
| Physique | Dirichlet | Neumann | Robin |
|---|---|---|---|
| Mécanique du solide | Déplacement | Traction (contrainte) | Ressort |
| Transfert thermique | Température | Flux de chaleur | Convection |
| Acoustique en pression | Pression acoustique | Accélération normale | Impédance |
| Courants électriques | Potentiel imposé | Courant imposé | Impédance |
Dans le contexte de la méthode des éléments finis, ces types de conditions aux limites auront différentes influences sur la structure du problème résolu.
Conditions de Neumann
Les conditions de Neumann sont des “chargements” et apparaissent dans le second membre du système d’équations. Dans COMSOL Multiphysics®, vous pouvez les voir sous forme de contributions faibles dans la Vue des équations. Les conditions de Neumann étant des contributions purement additives au second membre, elles peuvent contenir n’importe quelle fonction des variables: temps, coordonnées, valeurs de paramètres.
Considérons un problème de transfert thermique dans lequel une source de chaleur de rayon R se déplace dans la direction de l’axe x avec une vitesse v. Son intensité a une distribution parabolique avec une valeur maximale q_0. Une description mathématique de ce chargement pourrait être
Pour un chargement mobile, il est bien sûr impossible d’avoir des frontières de domaine, ou même un maillage, qui suit la distribution du chargement à chaque instant.
La distribution du chargement lui-même peut être entrée de manière simple. Etant donné que la variable de la coordonnée radiale, r, sera utilisée à deux endroits, il est judicieux de la définir comme une variable. Le tableau ci-dessous présente la totalité des données d’entrée de la source de chaleur mobile.
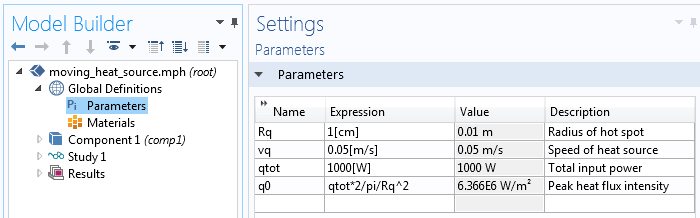
Paramètres décrivant la source de chaleur mobile.
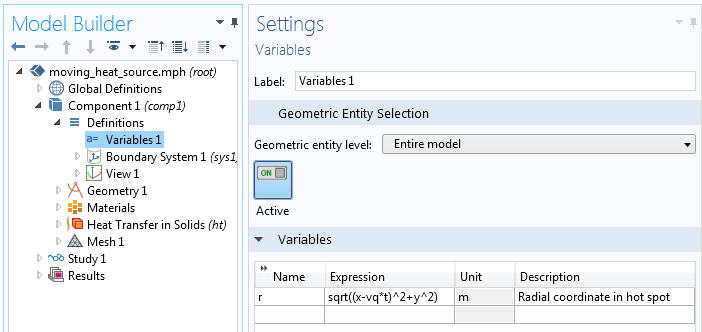
La variable décrivant la coordonnée radiale locale du centre actuel de la source de chaleur mobile.
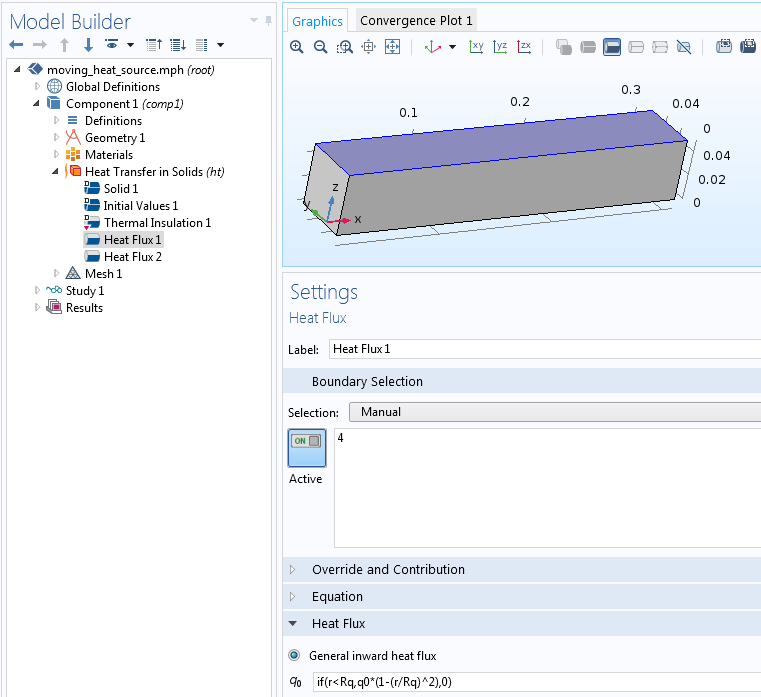
Paramètres pour le flux de chaleur.
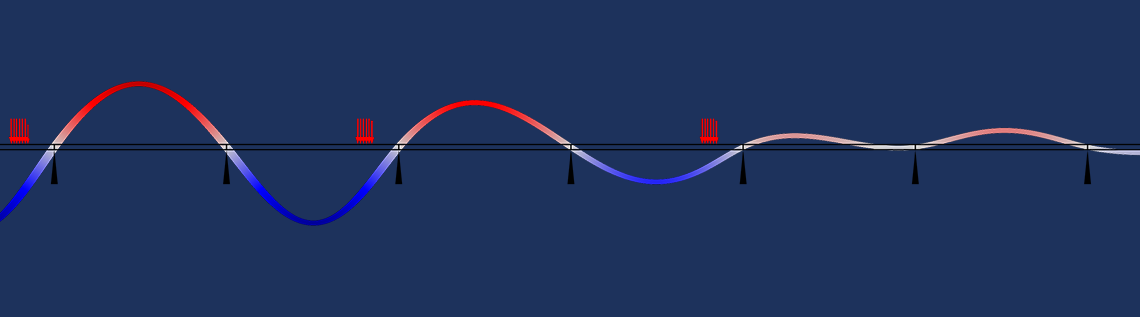
Les résultats de la simulation temporelle utilisant ces données sont présentés dans l’animation suivante. On suppose qu’il y a une symétrie selon le plan yz, le chargement est donc en fait appliqué sur le demi-cercle mobile.
Animation de la distribution de température lorsque la source de chaleur se déplace le long du barreau.
Conditions de Dirichlet
Lorsqu’une condition de Dirichlet est utilisée, la variable dépendante est imposée, il n’y a donc pas besoin de la résoudre. Les équations de ces degrés de liberté peuvent donc être éliminés du problème. Les conditions de Dirichlet modifient par conséquent la structure de la matrice de raideur. En regardant la Vue des équations dans COMSOL Multiphysics®, ces conditions apparaissent comme des contraintes.
Supposons que vous voulez que le point mobile impose une température de 450 K exactement. C’est peut-être un peu artificiel, mais cela montre une différence importante entre la condition de Neumann et la condition de Dirichlet. Si vous ajoutiez un noeud Temperature et entriez une expression similaire ( if(r < R,450[K],0)), cela reviendrait à imposer la température au zéro absolu sur la partie de la géométrie non couverte par le point chaud.
Or l’objectif est de désactiver la condition de Dirichlet hors du point chaud. Il y a une petite astuce pour cela. Si vous indiquez plutôt if(r < R,450[K],ht.Tvar) comme valeur imposée, vous aurez le comportement voulu (illustré dans l’animation suivante).
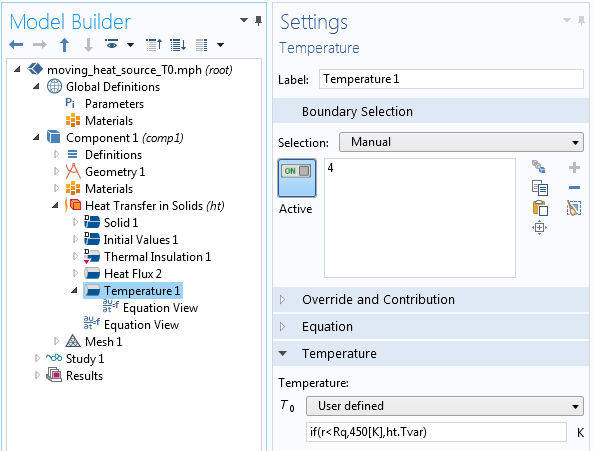
Réglages pour une condition de Dirichlet conditionnelle.
Animation de la distribution de température lorsque le point imposant la température se déplace le long du barreau.
Pour comprendre comment cela fonctionne, activez la Vue des équations, et regardez la mise en oeuvre de la condition de Dirichlet (dans ce cas, une température imposée):
Activation de la Vue des équations.
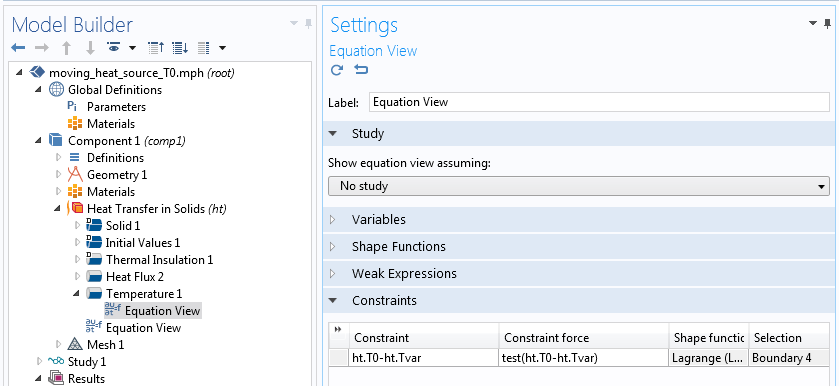
La Vue des équations pour le noeud de Température .
La contrainte est formulée comme suit, ht.T0-ht.Tvar, qui signifie implicitement ht.T0-ht.Tvar = 0. Le premier terme est la température imposée, que vous précisez comme donnée d’entrée. Le second terme est simplement le degré de liberté de la température sous forme de variable. Cela contraint la température à être égale à la valeur donnée, sauf si la valeur donnée correspond à la chaîne de caractères ht.Tvar. Dans ce cas, l’algèbre symbolique réduira l’expression à ht.Tvar-ht.Tvar pendant l’assemblage, puis à zéro. Et comme l’expression de la contrainte est 0, il n’y a pas de contrainte.
Contraintes faibles
Dans COMSOL Multiphysics®, il y a en fait deux implémentations disponibles pour la condition de Dirichlet. Le cas par défaut est la contrainte ponctuelle, comme mentionné ci-dessus, mais vous pouvez également utiliser une contrainte faible. Dans la contrainte faible, les équations sont ajoutées plutôt que supprimées. Les flux de chaleur nécessaires pour faire respecter les valeurs imposées de la température sont alors ajoutés en tant que degrés de liberté supplémentaires, qui sont des (multiplicateurs de Lagrange).
Vous pouvez utiliser quasiment la même astuce pour rendre une contrainte faible conditionnelle, avec une légère modification. Utiliser les contraintes faibles nécessite d’abord d’activer les Options avancées des physiques.
Activation des Options avancées des physiques.
Lorsque des contraintes faibles ont été sélectionnées dans un noeud au sein d’une interface physique, il y aura des degrés de liberté supplémentaires pour le multiplicateur de Lagrange. Dans notre cas, le degré de liberté a pour nom T_lm.
Si l’on applique la même expression pour la température que celle présentée ci-dessus, le degré de liberté supplémentaire ne donnera aucune contribution à la matrice de rigidité sur la partie de la frontière où la condition de Dirichlet est désactivée. La matrice de rigidité deviendra donc singulière. Pour éviter cette situation, modifiez if(r < R,450[K],ht.Tvar) en if(r < R,450[K],ht.Tvar-T_lm*1e-2). Le multiplicateur utilisé pour T_lm diffère selon les modèles et les champs physiques, et il peut nécessiter un certain réglage.
La raison pour laquelle cela fonctionne, comme un manuel pourrait le noter, est “laissée en exercice au lecteur”.
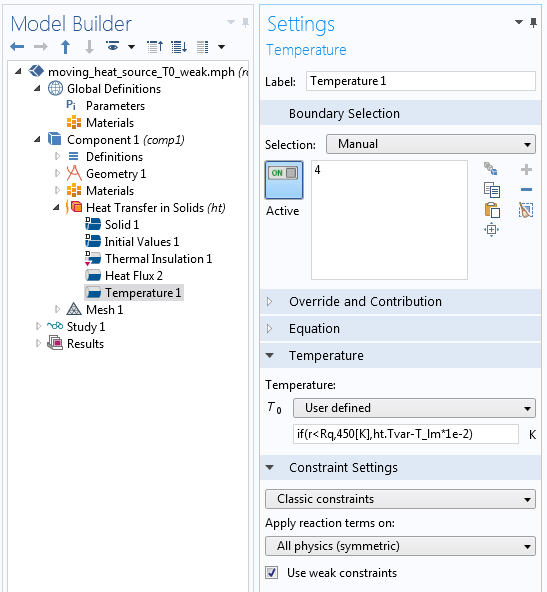
Paramètres pour une condition de Dirichlet conditionnelle lorsque les contraintes faibles sont utilisées.
Robin Conditions
Les conditions de Robin contribuent généralement à la fois à la matrice de rigidité et au second membre. La structure de la matrice de rigidité n’est pas modifiée, mais des valeurs sont ajoutées aux positions existantes. Les conditions de Robin apparaissent également comme des contributions faibles dans la Vue des équation. Transformer ces conditions en fonctions de temps, d’espace et d’autres variables est similaire à ce que l’on ferait pour des conditions de Neumann.
Il est toutefois intéressant de noter qu’en sélectionnant les valeurs appropriées, vous pouvez faire en sorte que les conditions Robin aient un comportement s’approchant de conditions de Dirichlet ou de Neumann. C’est particulièrement important dans les cas où vous souhaitez basculer entre les deux types de conditions limites au cours d’une simulation.
Pour créer une condition de Dirichlet, vous attribuez une valeur élevée à la “rigidité”, par exemple une constante de raideur de ressort ou un coefficient de transfert thermique. En termes mathématiques, il s’agit en fait d’une implémentation en pénalité de la condition de Dirichlet. Plus la rigidité est élevée, plus la précision de la valeur imposée pour le degré de liberté est grande. Mais il y a un bémol: une rigidité très élevée nuira au conditionnement numérique de la matrice de rigidité. Pour un problème de transfert thermique, un point de départ pour choisir un “grand” coefficient de transfert thermique \alpha pourrait être
où \lambda est la conductivité thermique et h une taille caractéristique d’élément.
La même approche peut être appliquée à d’autres domaines de la physique en remplaçant \lambda par la propriété matériau appropriée (par exemple, le module d’Young en mécanique des solides). Le facteur 1000 est simplemnt une suggestion et peut être remplacé par 104 ou 105.
Si vous deviez utiliser la convection pour modéliser la zone mobile de 450 K de l’exemple précédent, vous pourriez utiliser les paramètres indiqués ci-dessous. La variable prédéfinieh pour la taille de l’élément est utilisée dans l’expression.
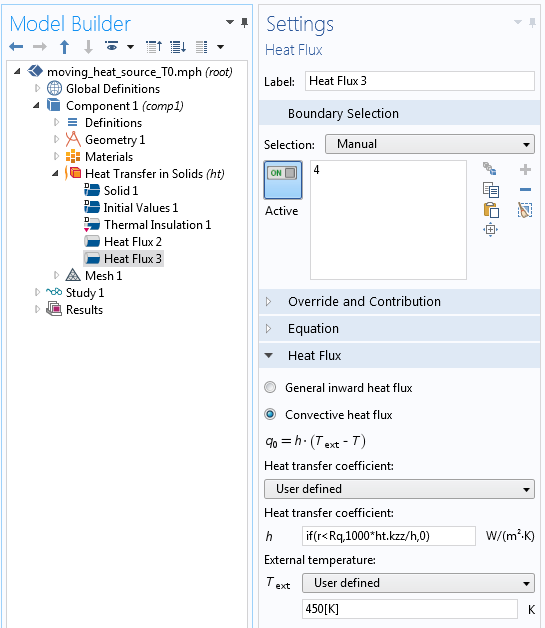
Utilisation d’une condition de convection pour imposer la température.
Lorsque j’ai commencé à utiliser l’analyse par éléments finis, il y a un certain temps déjà, il était parfois impossible d’imposer des déplacements non nuls dans les programmes d’éléments finis pour la mécanique des structures. La limitation venait de la complexité supplémentaire ajoutée par la programmation. Dans ce cas, la meilleure option était d’utiliser la méthode de pénalité en ajoutant un ressort rigide pré-déformé. Ceci dit il ne fallait pas qu’il soit trop rigide, car à l’époque, l’arithmétique en simple précision était encore utilisée !
Intéressons-nous maintenant à l’approximation d’une condition de Neumann. Nous souhaitons avoir un flux de chaleur indépendant de la température de surface. Dans le cas du transfert thermique, la condition de Robin implique que le flux de chaleur entrant q soit
où \alpha est le coefficient de transfert thermique, T la température à la frontière, et T_{\textrm{ext}} la température ambiante.
Par conséquent, si T_{\textrm{ext}} est beaucoup plus grande que la température attendue à la surface, alors q \approx \alpha T_{\textrm{ext}}. La stratégie consiste alors à choisir un T_{\textrm{ext}} arbitraire et très grand et à calculer un coefficient de transfert thermique approprié, comme indiqué ci-dessous.
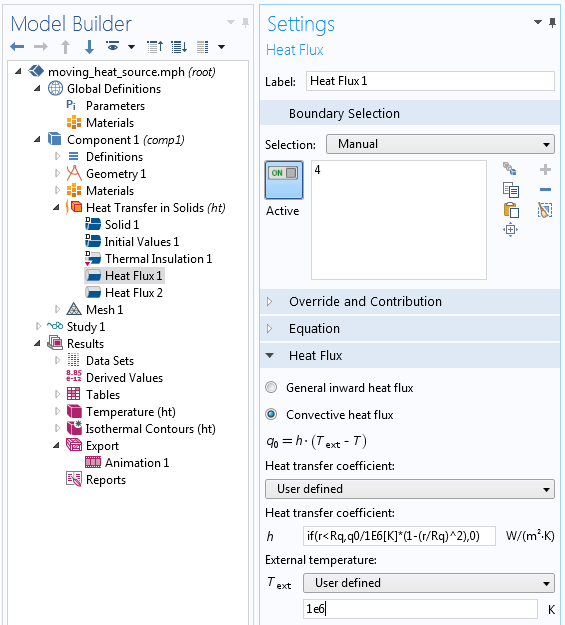
Utilisation d’une condition de convection pour imposer le flux de chaleur.
Les concepteurs utilisent en fait ce principe pour introduire une force imposée dans des composants mécaniques réels : un long ressort faible précontraint. Si la prédéfomation du ressort est bien supérieure au déplacement des pièces auxquelles il est relié, la force dans le ressort sera presque constante.
Résolution des erreurs de discrétisation
Lorsqu’une condition aux limites est limitée par une expression booléenne telle que if(r < ; R,..., il est plus que probable que la frontière de la région à laquelle elle est appliquée ne suivra pas les arêtes des éléments du maillage. Cela introduira alors des erreurs de discrétisation.
Pour une condition de Neumann ou de Robin, une intégration numérique est effectuée sur chaque élément fini. La valeur de la fonction est évaluée en un certain nombre de points de Gauss discrets dans l’élément. Si la taille des éléments du maillage est grande par rapport à la taille géométrique du chargement, alors le nombre exact de points de Gauss couverts par le chargement peut affecter significativement le chargement total. Il faudrait donc qu’il y ait plusieurs éléments sur la zone couverte par le chargement à chaque instant.
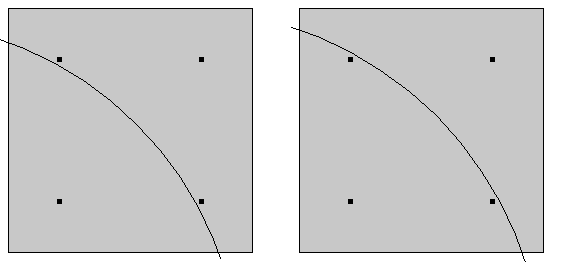
Une légère modification dans l’emplacement du chargement peut modifier le nombre de points d’intégration contributant. (En réalité, le nombre de points d’intégration est plus grand.)
Les conditions de Dirichlet, au moins au sens ponctuel, sont au contraire appliquées aux noeuds du maillage. Dans la figure ci-dessous, la distribution de la température et le flux de chaleur sont affichés à un instant donné lors de la simulation du point circulaire mobile imposant une température de 450 K. Devant le point chaud, une ombre plus foncée de 260 K est visible. Etant donné que les températures initiales et ambiantes dans la simulation sont de 293 K, ceci n’est pas attendu. Il s’agit d’un artefact numérique lié au fait que tous les noeuds de chaque élément n’ont pas une condition de Dirichlet. Une discontinuité au niveau d’une condition de Dirichlet entraînera des singularités. C’est un sujet de discussion traité dans un article de blog précédent. Raffiner le maillage réduira ce type d’effet.
Les flèches vertes de la figure suivante représentent les noeuds au niveau desquels un flux de chaleur entrant est généré en réaction à la température imposée. Avec la densité de maillage du modèle, l’approximation d’un demi-cercle sera assez grossière.
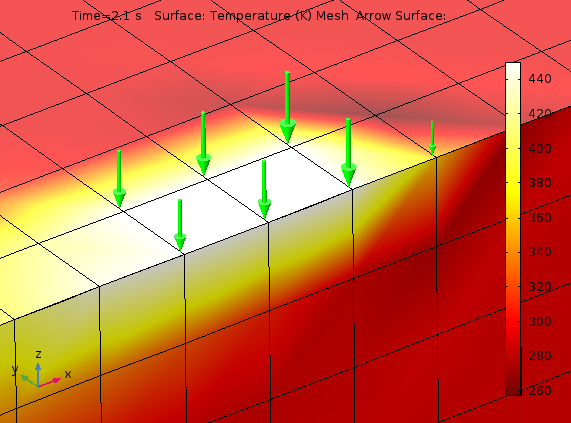
Distribution de température et flux de chaleur autour de la température semi-circulaire imposée.
Dépendance à la solution dans les conditions aux limites
La solution peut intervenir dans vos conditions aux limites de nombreuses façons. Cela introduira généralement des non-linéarités, qui sont automatiquement détectées par COMSOL Multiphysics®.
Prenons l’exemple d’une poutre dont l’appui est placé légèrement en dessous d’elle, ce qui empêche tout mouvement supplémentaire au delà d’une certaine déflexion. Cela peut être implémenté à l’aide d’une condition de Dirichlet conditionnelle via un noeud de Déplacement/Rotation imposée dans l’interface Poutre.

Poutre avec une déflexion, un appui de contrôle et un chargement distribué.
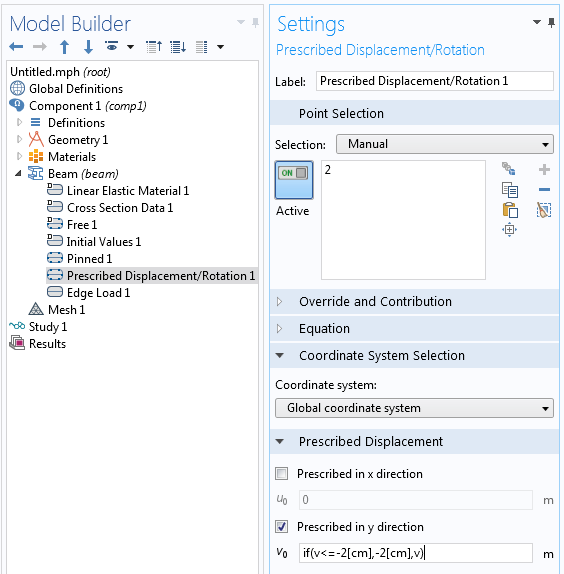
Réglages imposant que le déplacement de la poutre s’arrête lorsque la déflexion dépasse 2 cm.
L’analyse montre le comportement attendu. Pour de faibles chargements, la déflexion présente une symétrie, tandis qu’aux chargements plus élevés, le point de la poutre où se trouve l’appui supplémentaire cessera de bouger. Au dernier niveau de chargement, la poutre subira même un changement de signe dans la courbure. Ce phénomène est visible dans le graphique de déformation, mais il apparaît plus clairement dans un graphique de moment de flexion.
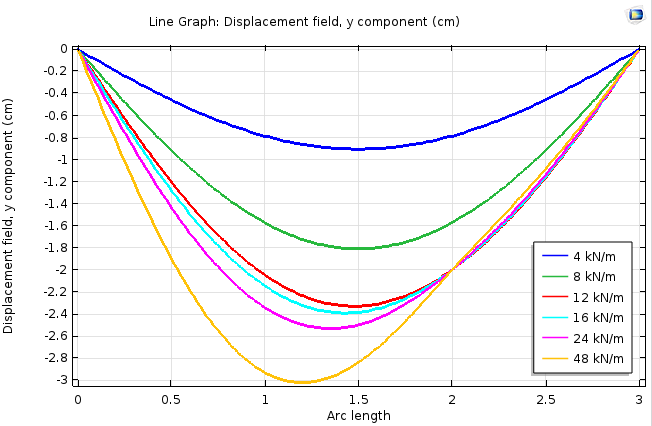
Le déplacement du point d’appui de la poutre s’arrête à 2 cm.
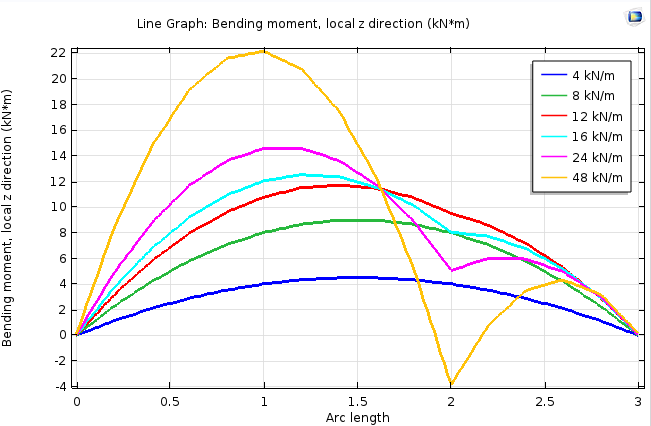
Moment de flexion le long de la poutre à différents niveaux de chargement.
L’approche mise en évidence ici est plutôt grossière et la solution itérative pourrait ne pas avoir de bonnes propriétés de convergence. Une mise en œuvre plus stable consiste à utiliser un ressort fortement non-linéaire au point d’appui, afin que la force de réaction soit une fonction continuellement différentiable du déplacement. C’est en fait similaire à la façon dont le contact en pénalité est implémenté dans l’interface de Mécanique du solide.
Conclusions sur l’utilisation de conditions aux limites dans COMSOL Multiphysics®
COMSOL Multiphysics® vous donne accès à des mécanismes très puissants pour imposer des conditions aux limites atypiques. Nous avons présenté ici quelques exemples de ce que vous pouvez faire avec ces conditions.
Pour ceux d’entre vous qui sont intéressés par l’analyse d’un modèle avec un chargement mobile, vous pouvez jeter un oeil au Tutoriel de charge mobile, disponible dans la Bibliothèque d’Applications.
Si vous avez d’autres questions sur la façon d’imposer des conditions aux limites atypiques dans le cadre de vos projets de modélisation, nous vous invitons à nous recontacter.







Commentaires (0)