
On nous demande souvent comment évaluer au mieux les différentes quantités de contraintes dans le logiciel COMSOL Multiphysics® qui donne accès à de nombreuses variables de contraintes et à différentes options de visualisation des résultats. Dans cet article de blog, nous allons approfondir toutes ces questions. Nous nous concentrerons sur le fonctionnement général de l’évaluation des résultats avant de nous pencher sur les spécificités liées à l’analyse des contraintes.
Table des matières
- En quoi les contraintes sont-elles si spéciales ?
- Quelques notions d’éléments finis
- Continuité physique des flux
- Moyenne entre les éléments
- Où les résultats sont-ils évalués ?
- Comment les contraintes sont-elles calculées ?
- Un cas particulier: la dilatation thermique
- Etats définis aux points de Gauss
- Évaluation de valeurs maximales
- Quels résultats de contrainte devrais-je afficher ?
- Conclusion
En quoi les contraintes sont-elles si spéciales ?
Dans de nombreux domaines de la physique, la principale quantité d’intérêt est le champ lui-même et non ses gradients. En thermique, par exemple, vous vous intéressez généralement à la température, tandis que les gradients de température et les flux de chaleur détaillés passent au second plan. En revanche, en mécanique des structures, les contraintes et déformations locales sont souvent plus importantes que les déplacements. Dans la plupart des cas, des contraintes élevées seront à l’origine de la rupture, que ce soit de manière statique ou par fatigue. Il est donc important de disposer de méthodes fiables pour évaluer des contraintes.
Quelques notions d’éléments finis
Dans la méthode des éléments finis, la géométrie est subdivisée en petits domaines appelés éléments finis, qui forment un maillage. Dans chaque élément, une hypothèse est faite quant à la variation du champ à résoudre. Ce dernier est approximé par des fonctions de forme, qui sont le plus souvent des polynômes linéaires ou quadratiques dépendant des coordonnées. Le champ peut être scalaire ou vectoriel.
Tous les éléments sont connectés les uns aux autres par les noeuds du maillage. En considérant l’équilibre de certains flux, il est possible d’établir un système d’équations pour la valeur du champ sur tous ces noeuds.
Les champs résolus pour quelques cas classiques sont résumés dans le tableau ci-dessous:
| Physique | Champ | Gradient | Flux |
|---|---|---|---|
| Mécanique du solide | Déplacement (vecteur) | Déformation (tenseur) | Contrainte (tenseur) |
| Transfert de chaleur | Température (scalaire) | Gradient de température (vecteur) | Flux de chaleur (vecteur) |
| Diffusion | Concentration (scalaire) | Gradient de concentration (vecteur) | Flux massique (vecteur) |
| Electrostatique | Potentiel électrique (scalaire) | Champ électrique (vecteur) | Déplacement électrique (vecteur) |
Lorsque les équations issues de l’approximation par éléments finis sont résolues, la variable dépendante (degré de liberté ou DOF) est connue sur tous les noeuds du maillage. Le champ est continu sur l’ensemble de la géométrie et les valeurs en tout point d’un élément sont définies de manière unique à partir des valeurs aux noeuds et du polynôme d’interpolation choisi (c’est-à-dire la fonction de forme).
Toutefois, le gradient d’un champ n’est généralement pas continu d’un élément à l’autre. Au sein d’un élément, il est déterminé par les dérivées spatiales des fonctions de forme et les valeurs du champ aux noeuds de l’élément individuel. Ainsi, les gradients sont également définis de manière unique à l’intérieur de chaque élément, mais pas aux frontières de l’élément. Les flux sont ensuite calculés à partir des gradients. Dans les cas linéaires, il s’agit d’une simple multiplication du gradient par un paramètre matériau donné.
Continuité physique des flux
Il est important de comprendre que, pour des raisons physiques, les flux sont dans une large mesure continus. Ce qui sort d’un élément doit entrer dans le suivant. Seule la représentation numérique n’est pas continue. La solution par éléments finis convergera toutefois vers la vraie solution continue à mesure que le maillage sera raffiné. Malheureusement pour ceux d’entre nous qui travaillent avec les contraintes, la convergence des gradients est plus lente que celle du champ lui-même.
Les propriétés de continuité des gradients et des flux ne sont cependant pas triviales. Lorsqu’il existe une frontière entre deux matériaux différents, seules certaines composantes des flux et des gradients sont continues.
En règle générale, le flux est continu dans la direction normale à la frontière mais pas dans la direction tangentielle. Pour les gradients, c’est le contraire.
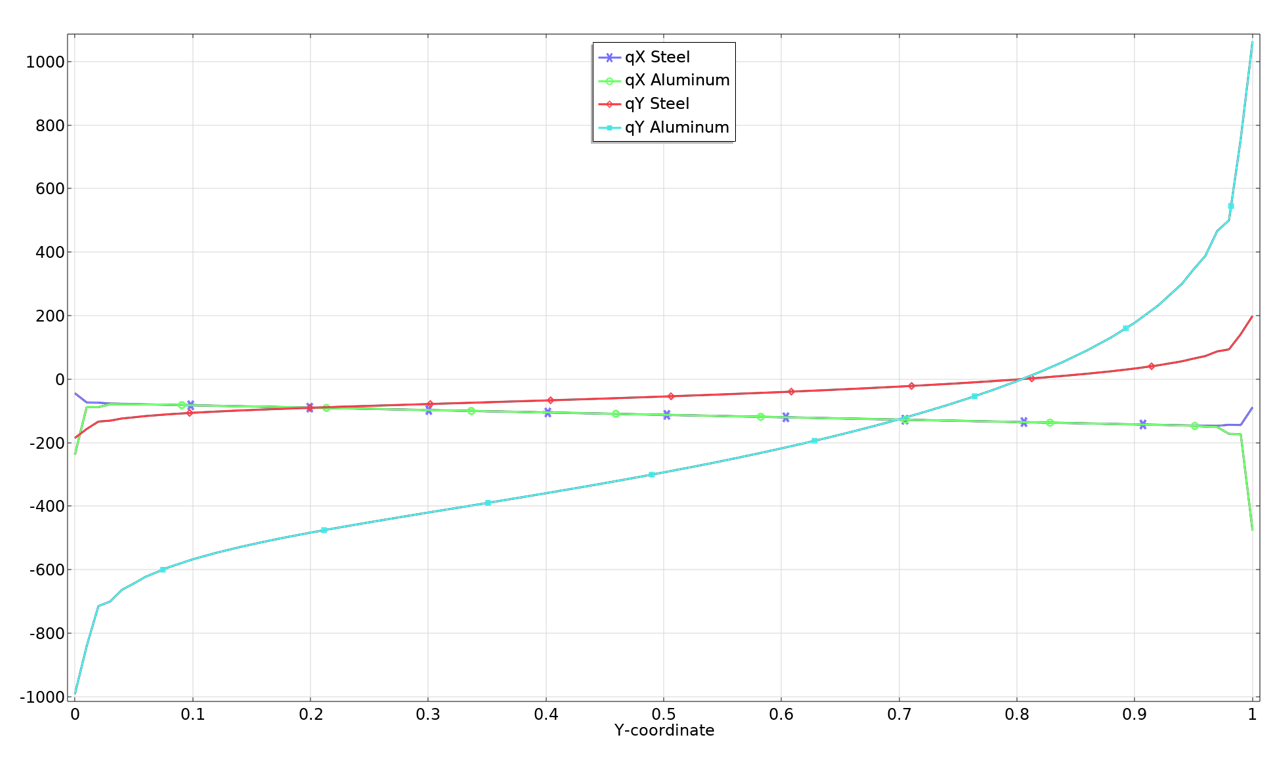
Dans l’exemple ci-dessous, on étudie le transfert de chaleur stationnaire dans un rectangle composé de deux carrés présentant des propriétés matériaux différentes.
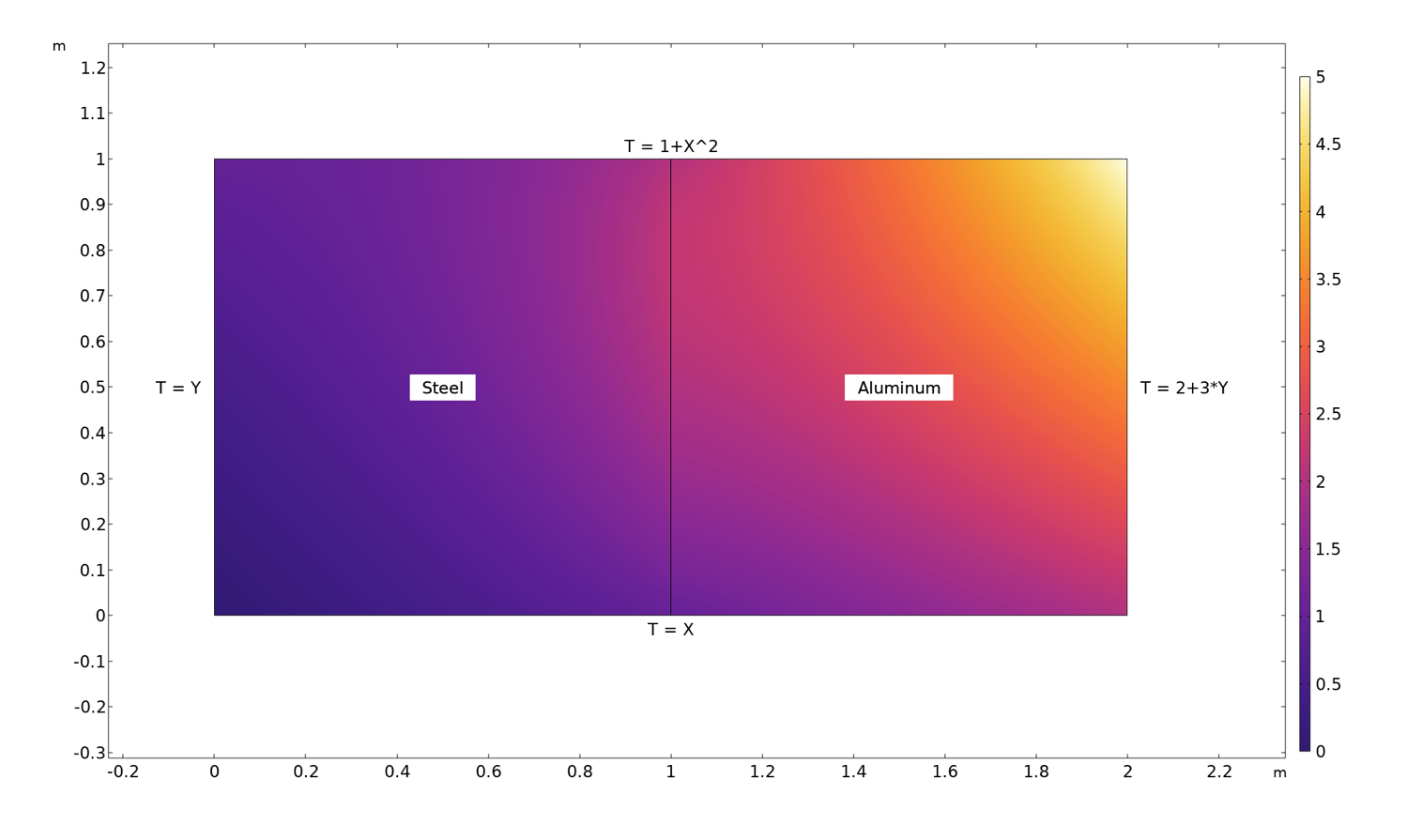
Distribution de température dans un rectangle composé d’un carré d’acier et d’un carré d’aluminium. La température est imposée le long sur toutes les frontières selon les valeurs indiquées dans la figure.
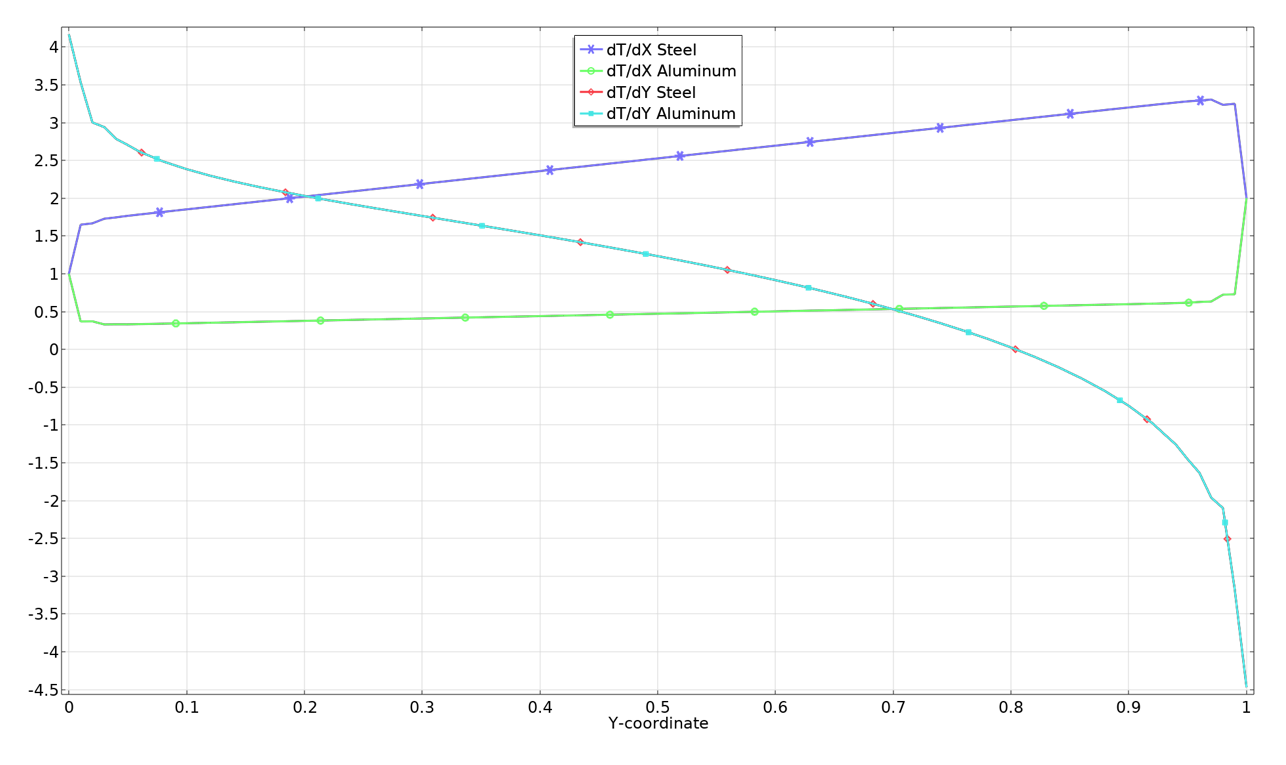
En traçant les gradients de température et les flux de chaleur le long de la frontière séparant les deux domaines, on peut visualiser les propriétés de continuité.
Gradients de température (à gauche) et flux de chaleur (à droite) le long de la frontière séparant les deux matériaux.
Comme prévu, le gradient de température dans la direction y, ainsi que le flux dans la direction x, sont identiques des deux côtés de l’interface. Si nous avions fait le même exercice pour la mécanique du solide, nous aurions constaté la continuité de deux composantes de contrainte, \sigma_\mathrm{x} et \tau_\mathrm{xy}, ainsi que d’une composante de déformation, \varepsilon_\mathrm{y}. Une autre façon de voir les choses est que les composantes du flux que l’on peut imposer sur une frontière libre doivent également être continues sur une frontière interne.
Il convient de noter que la plupart des invariants, tels que les contraintes équivalentes ou les normes de flux, présentent un saut au niveau d’une discontinuité de matériau, étant donné que certaines composantes du tenseur ou du vecteur constitutif ne sont pas continues.
Moyenne entre les éléments
Puisque la plupart des quantités que nous étudions sont connues pour être continues, il est tentant de faire la moyenne, par exemple, des contraintes entre les éléments. C’est d’ailleurs ce qui est fait par défaut dans la plupart des cas. Souvent, il permet non seulement d’améliorer l’impression visuelle, mais aussi de s’approcher davantage de la vraie solution après convergence
Vous pouvez contrôler si, et comment, la moyenne (ou, selon la terminologie de la présentation des résultats, le lissage) est appliquée. La clé est la section Qualité, disponible pour la plupart des noeuds de visualisation des résultats.
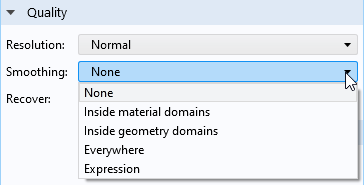
Options de lissage.
Les différentes options de lissage sont résumées dans le tableau ci-dessous:
| Choix | Effet |
|---|---|
| Aucun | Pas de lissage entre éléments adjacents. |
| A l’intérieur des domaines matériaux | Le lissage est effectué entre les éléments adjacents appartenant au même domaine matériau. Un domaine matériau est, dans sa forme la plus simple, un ensemble de domaines auxquels le même matériau a été affecté. Certaines interfaces physiques utilisent cependant leurs propres définitions. Par exemple, dans l’interface Coque, les éléments appartiennent au même domaine matériau seulement s’ils sont constitués du même matériau, s’ils ont la même épaisseur, et s’ils ne sont pas reliés par une ligne de pliage. Notez qu’il s’agit de l’option par défaut lorsque vous ajoutez un nouveau graphique. |
| A l’intérieur des domaines géométriques | Le lissage est effectué entre les éléments adjacents appartenant au même domaine géométrique, mais pas sur les frontières du domaine. |
| Partout | Le lissage est effectué entre tous les éléments adjacents. |
| Expression | Le lissage est effectué lorsqu’une expression booléenne définie par l’utilisateur est évaluée à une valeur non nulle. |
Lorsque le lissage est activé, vous pouvez également spécifier un seuil sur la différence de valeurs nodales entre les éléments adjacents, au-delà duquel le lissage sera désactivé. L’idée est d’obtenir un compromis permettant de présenter des graphiques lisses et agréables à lire sans pour autant masquer d’importantes discontinuités.
Depuis la version 6.0 du logiciel COMSOL®, les graphiques de contraintes générés par défaut par les interfaces de mécanique des structures exploitent cette fonctionnalité. Par défaut, le seuil est fixé à 0.2, mais vous pouvez modifier cette valeur en fonction de vos besoins.
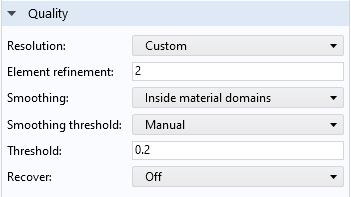
La section Qualité d’un graphique par défaut de l’interface Mécanique du solide. Avec la valeur seuil par défaut de 0.2, un écart maximal de 20% est accepté pour le lissage.
La figure ci-dessous présente des exemples de différents types de lissage pour un graphique de contraintes issu d’un modèle de mécanique du solide en 2D comportant un seul matériau. Afin d’accentuer les effets, des éléments triangulaires de premier ordre sont utilisés. Il s’agit d’éléments peu performants, dans lesquels les déformations et les contraintes sont uniformes. En regardant la figure, il est important de noter que:
- Sans aucun lissage (en bas à gauche), chaque élément de maillage est clairement visible.
- Avec un lissage entre tous les éléments (en bas au centre), l’impression visuelle est bien meilleure qu’en l’absence de lissage. L’accord avec la solution “correcte” à haute résolution obtenue à l’aide d’un maillage fin et de fonctions de forme quadratiques (en bas à droite) est satisfaisant. Toutefois, certains détails de la région fortement contrainte ne sont pas fidèlement représentés.
- Comme un seul matériau est utilisé dans cet exemple, il n’y a pas de différence entre les options Partout (en bas au centre) et A l’intérieur des domaines matériaux.
- Lorsque l’option A l’intérieur des domaines géométriques est utilisée (en haut à droite), le lissage est appliqué à l’intérieur de chaque domaine, mais les sauts de contrainte entre les domaines sont bien visibles. Si des matériaux différents avaient été attribués aux différents domaines, le même graphique serait obtenu avec l’option A l’intérieur des domaines matériaux.
- Les paramètres par défaut en mécanique des structures sont utilisés dans l’option A l’intérieur des domaines matériaux (en haut à gauche). Notez que les sauts de contrainte sont clairement visibles là où les contraintes sont mal résolues, alors que les contours sont lisses là où les gradients sont moins prononcés. Avec ce type de graphique, vous obtenez le meilleur des deux mondes: une vue d’ensemble globalement lisse, et faisant ressortir les régions dont la résolution est insuffisante.
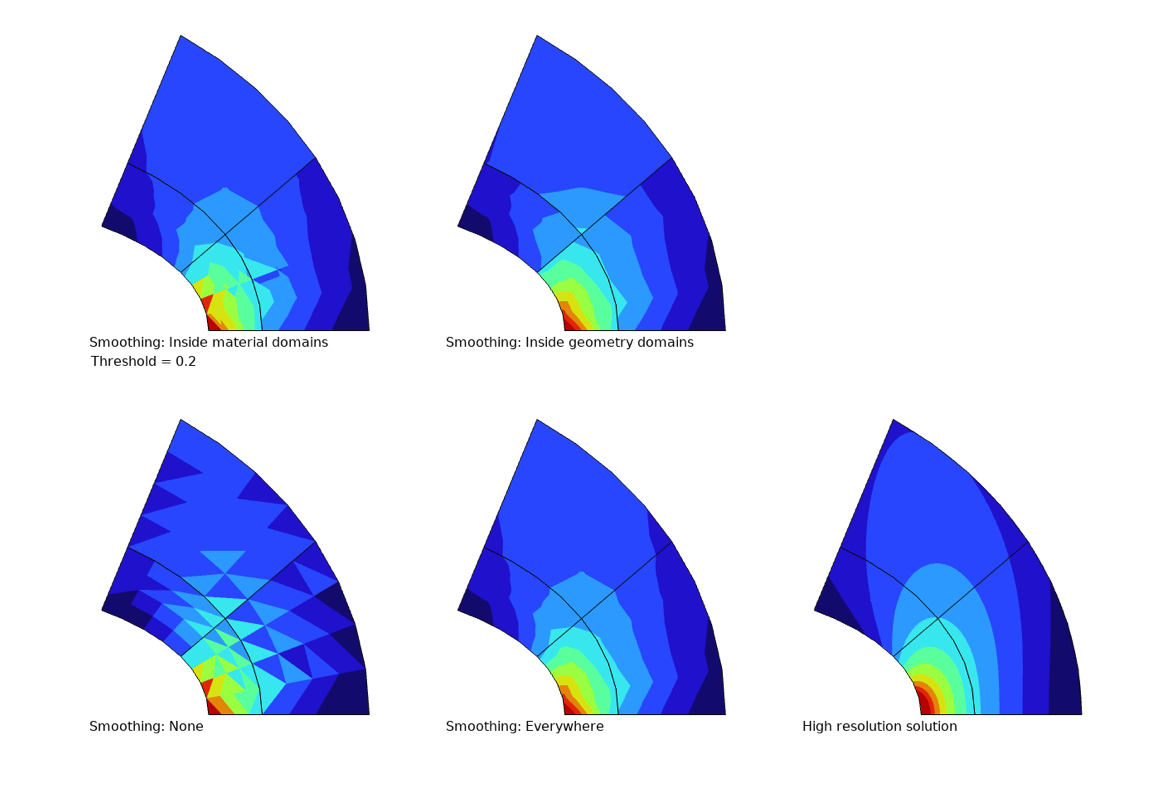
Les effets des différents types de lissage.
Jusque-là, nous nous sommes intéressés à la question des moyennes et des sauts dans les graphiques de volumes, de surfaces et d’isovaleurs. Les graphiques sur ligne présentent une complexité supplémentaire. Si la ligne comporte une ou plusieurs surfaces adjacentes, il est nécessaire de calculer la moyenne selon deux directions:
- Le long de la ligne, indépendamment du fait que la ligne soit connectée à une ou plusieurs surfaces. Cette opération s’effectue de la même manière que celle décrite ci-dessus, et la même section Qualité est disponible.
- A travers la ligne, entre les surfaces adjacentes s’il y en a plus d’une. Cette opération est effectuée avant toute autre et et de façon inconditionnelle.
Si la quantité à représenter n’est pas continue sur la ligne, la valeur moyenne n’est plus pertinente ; il convient alors de tracer un graphique par frontière (3D) ou par domaine (2D). Pour remédier à cela, il est nécessaire de faire appel à des opérateurs particuliers.
Si la ligne représente une frontière en 2D, vous pouvez utiliser les opérateurs up() et down() pour préciser dans quel domaine les résultats doivent être pris. Les côtés “up” et “down” (“supérieur” et “inférieur”) correspondent à l’orientation du vecteur normal sur la frontière. Cette méthode a été utilisée dans les graphiques de flux de chaleur visibles plus haut. Dans le graphique ci-dessous, les gradients de température selon la direction x, évalués sur chaque domaine, sont comparés au résultat moyenné. De toute évidence, le calcul par défaut de la moyenne n’est pas le meilleur choix lorsqu’il y a une discontinuité physique lors du franchissement de la frontière.

Gradient de température selon la direction x: valeur moyenne et valeurs dans chaque domaine.
La même technique peut également être utilisée en 3D, pour les graphiques de surface définis sur des frontières internes. Dans ce cas, on ne peut évidemment tracer la valeur que d’un seul côté à la fois.
Si la ligne sélectionnée est une arête en 3D, les choses sont un peu plus compliquées, puisqu’il peut y avoir un nombre arbitraire de frontières partageant cette arête. Dans ce cas, vous devez utiliser l’opérateur side() pour extraire les valeurs des frontières individuelles. L’opérateur peut être appelé de la façon suivante: side(12,shell.mises), où le premier argument désigne le numéro de la frontière. Vous devez donc en premier lieu déterminer le numéro de la frontière dans laquelle vous souhaitez évaluer le résultat. On peut pour cela simplement créer un graphique de surface de la variable prédéfinie dom, puis cliquer sur la frontière souhaitée pour voir son numéro.
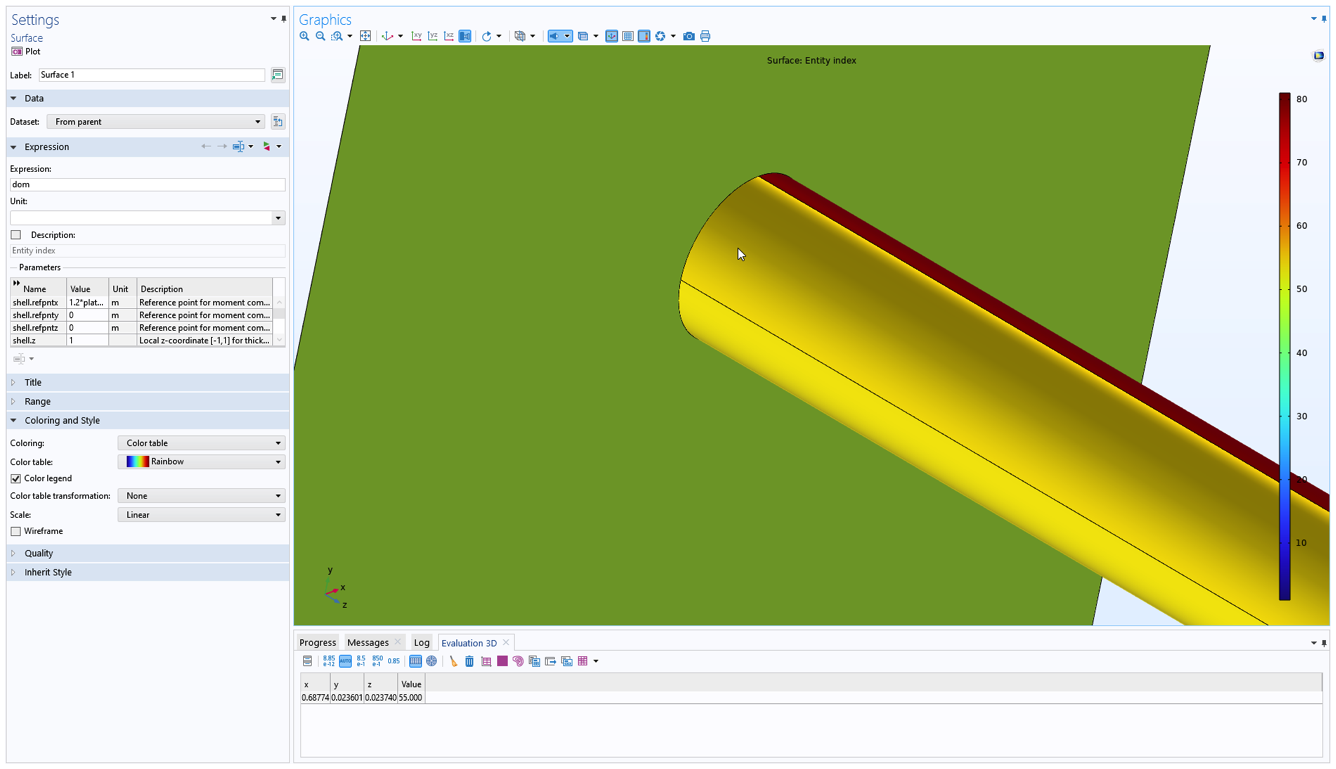
Trouver le numéro d’une frontière à l’aide d’un graphique de surface.
Une autre méthode pour trouver le numéro d’une frontière consiste à se rendre sur n’importe quel noeud de l’arborescence du Constructeur de modèles comportant une sélection de frontière, puis à passer le pointeur de la souris sur la frontière en question. Le numéro de celle-ci sera affiché dynamiquement dans le coin supérieur gauche de la fenêtre Graphiques.
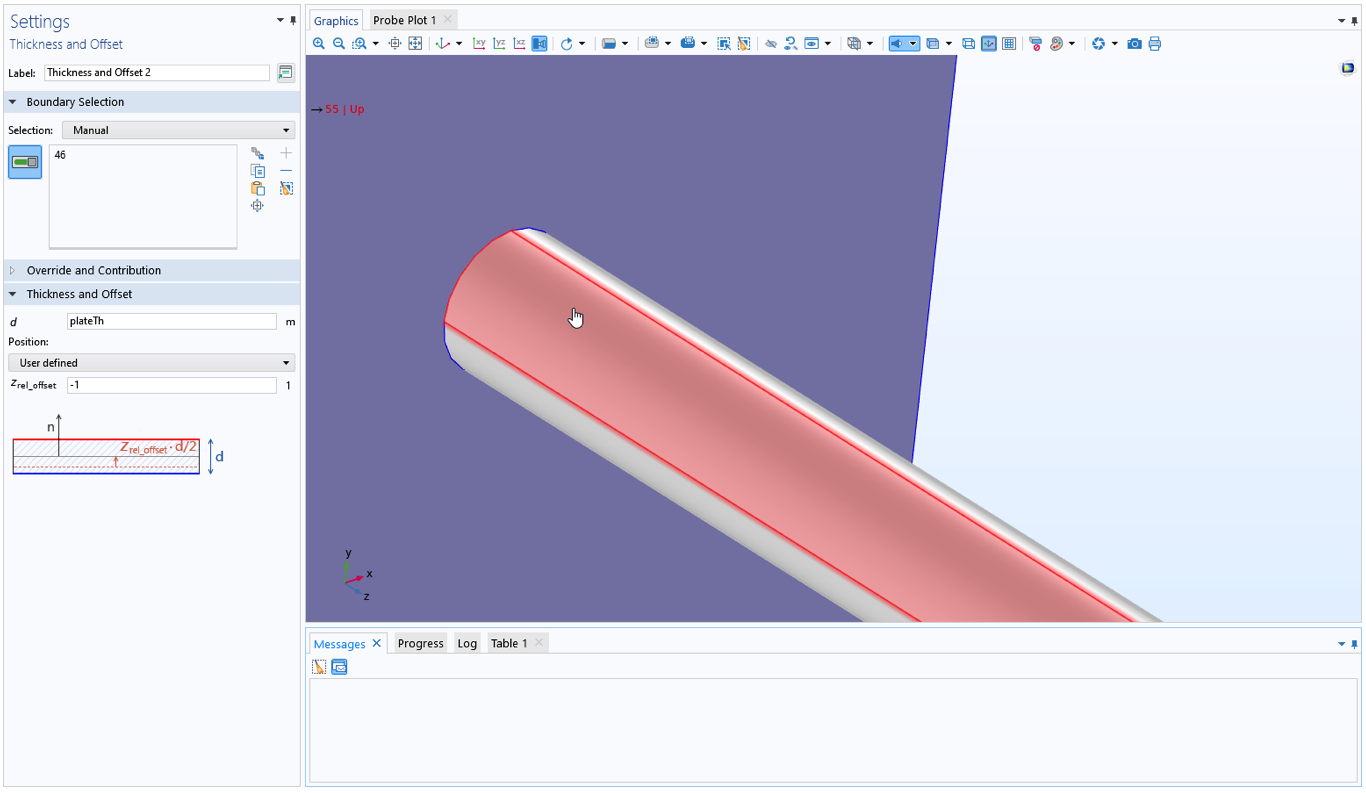
Trouver le numéro d’une frontière à l’aide d’une sélection de frontières.
Où les résultats sont-ils évalués ?
Lors de la création de graphiques de surface ou de graphiques sur ligne, l’expression à représenter est généralement évaluée en plusieurs points à l’intérieur de chaque élément, de chaque frontière d’élément ou de chaque arête. Le nombre de points d’évaluation est contrôlé par le réglage Résolution dans la section Qualité.
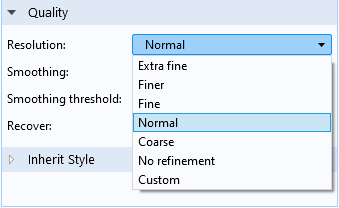
Options disponibles pour la Résolution.
Lorsque l’une des résolutions prédéfinies est sélectionnée, le nombre de points évalués dépend de plusieurs facteurs tels que la taille du modèle et la dimension de l’espace. L’utilisation d’une résolution élevée donnera généralement des tracés plus détaillés à l’intérieur des éléments. Toutefois, cela n’est utile que si l’expression évaluée présente un degré élevé de régularité à l’intérieur de l’élément. Si ce n’est pas le cas, cela ne fera que générer des fluctuations parasites.
Comment les contraintes sont-elles calculées ?
Jusqu’ici, nous avons principalement abordé les options générales de visualisation des résultats. Lorsqu’il s’agit de représenter des contraintes, il faut tenir compte en plus de la manière dont elles sont calculées à l’intérieur de chaque élément.
Les déformations totales étant simplement dérivées des déplacements, elles sont toujours lisses. Les contraintes, cependant, sont souvent le résultat d’une combinaison de plusieurs effets distincts. La manière exacte dont les contraintes sont calculées dépend de la loi de comportement principale et du fait que la non-linéarité géométrique soit prise ou non en compte. Pour expliquer les principes généraux, supposons que la loi de comportement principale soit linéaire élastique et que l’analyse soit géométriquement linéaire.
Le tenseur des contraintes, \sigma, est alors calculé de la manière suivante:
Ici, C est le tenseur d’élasticité, \varepsilon_\mathrm{el} est la déformation élastique et \sigma_\mathrm{add} sont les éventuelles contributions de contraintes additionnelles. La déformation élastique est la différence entre la déformation totale \varepsilon_\mathrm{tot}, calculée à l’aide des fonctions de forme et des déplacements nodaux, et tout champ de déformation inélastique \varepsilon_\mathrm{inel}.
Voici quelques exemples de déformations inélastiques:
- La dilatation thermique
- Le gonflement hygroscopique
- La plasticité
- Le fluage
- Les déformations initiales
Voici quelques exemples contributions de contraintes additionnelles:
- Les contraintes viscoélastiques
- Les contraintes d’amortissement
- Les contraintes initiales
Ainsi, la contrainte totale est en général la somme de plusieurs contributions distinctes. En particulier, \varepsilon_\mathrm{tot} et \varepsilon_\mathrm{inel} sont souvent du même ordre de grandeur, de sorte que le tenseur des déformations élastiques fait apparaître des petites valeurs obtenues par soustraction de deux ou plusieurs valeurs plus élevées. C’est le cas, par exemple, des dilatations thermiques non contraintes ou des grandes déformations plastiques.
Alors pourquoi cela pose-t-il un problème ? Si les différentes contributions à la contrainte et à la déformation ne sont pas représentées par le même type d’interpolation sur l’élément, il peut y avoir d’importantes fluctuations locales, même si les résultats sont en moyenne cohérents.
Un cas particulier: la dilatation thermique
Profitons d’un petit détour pour étudier un cas fréquent dans lequel cela peut se produire. La communauté des spécialistes des éléments finis a observé très tôt que des motifs de contrainte “ondulés” pouvaient apparaître dans les analyses thermomécaniques. Les contraintes thermiques étant proportionnelles à la température, \varepsilon_\mathrm{inel} aura alors une variation quadratique au sein de chaque élément. Les déformations totales, cependant, sont des dérivées des fonctions de forme du déplacement et présenteront donc une distribution linéaire. Dans ce cas, la déformation élastique est obtenue par différence entre une fonction linéaire et une fonction quadratique. Il en résulte un profil de déformation élastique (et donc de contrainte) singulier à l’intérieur de chaque élément. C’est pourquoi il a parfois été recommandé de résoudre le problème thermique à l’aide de fonctions de forme linéaires lorsque les températures étaient utilisées pour piloter la dilatation thermique d’un solide. Dans COMSOL Multiphysics®, ce problème est traité en interne par le couplage multiphysique Dilatation thermique (ainsi que par les fonctionnalités Gonflement hygroscopique et Contrainte d’intercalation). Le champ de déformation inélastique est réinterpolé à un ordre polynomial correspondant aux déformations calculées à partir du champ de déplacement. Cela permet de réduire les artefacts dans la solution de contrainte locale.
Etats définis aux points de Gauss
Il existe un autre type de déformation inélastique qui n’implique pas de champ du tout mais plutôt des états locaux stockés ponctuellement aux points d’intégration (points de Gauss). Pour en apprendre plus sur les points de Gauss, vous pouvez consulter l’article de blog “Introduction à l’intégration numérique et aux points de Gauss”. La plupart des lois de comportement non-linéaires, comme la plasticité et le fluage, fonctionnent de cette manière. Dans ce cas, l’évaluation des contraintes en un point quelconque de l’élément devient plus compliquée.
Si vous évaluez une composante de contrainte, comme solid.sx, elle est en fait calculée “à la volée” en chaque point de l’élément. Dans ce cas, la loi non-linéaire du matériau est évaluée en utilisant les valeurs stockées à partir du point de Gauss le plus proche. Si les déformations inélastiques varient fortement sur l’élément, cela peut induire des erreurs significatives. L’évaluation de la loi de comportement peut même échouer, alors même que celle-ci est bien évaluée aux points de Gauss.
Il est préférable de créer une approximation lisse basée sur les valeurs aux points de Gauss, ce qui est possible avec l’opérateur gpeval(). Si vous appelez, par exemple, gpeval(4,solid.sx) plutôt que solid.sx, vous obtiendrez un champ de contraintes lisse sur l’élément. Dans ce cas, la relation non-linéaire contrainte-déformation est évaluée uniquement aux points de Gauss où elle est déjà satisfaite. Ensuite, pour générer un champ continu, on utilise un ajustement par moindres carrés des valeurs aux points de Gauss.
Dans sa version brute, l’opérateur gpeval() vous demande de fournir l’ordre d’intégration approprié en premier argument. Heureusement, dans la plupart des cas, vous n’aurez pas à vous en préoccuper. Plusieurs variables prédéfinies sont déjà disponibles dans les interfaces physiques, comme par exemple solid.sGpx et solid.misesGp. Si vous ne trouvez pas de variable intégrée adéquate pour votre expression, vous pouvez utiliser un opérateur propre à l’interface physique, par exemple, solid.gpeval(expr), qui incorpore déjà l’ordre d’intégration approprié.
Dans l’exemple ci-dessous, différentes options d’évaluation sont examinées pour un champ stocké aux points de Gauss (par une variable dépendante définie par l’utilisateur et appelée myDOF). Le modèle est constitué d’un seul élément 2D, dont les coordonnées x et y sont comprises entre 0 et 1. Le champ est décrit par l’expression (Y+1)/(2*X+1). Un schéma de 3×3 points de Gauss est utilisé, de sorte qu’il y aura neuf valeurs indépendantes stockées. Ces valeurs correspondent exactement à celles du champ d’origine, évaluées en chaque point de Gauss.
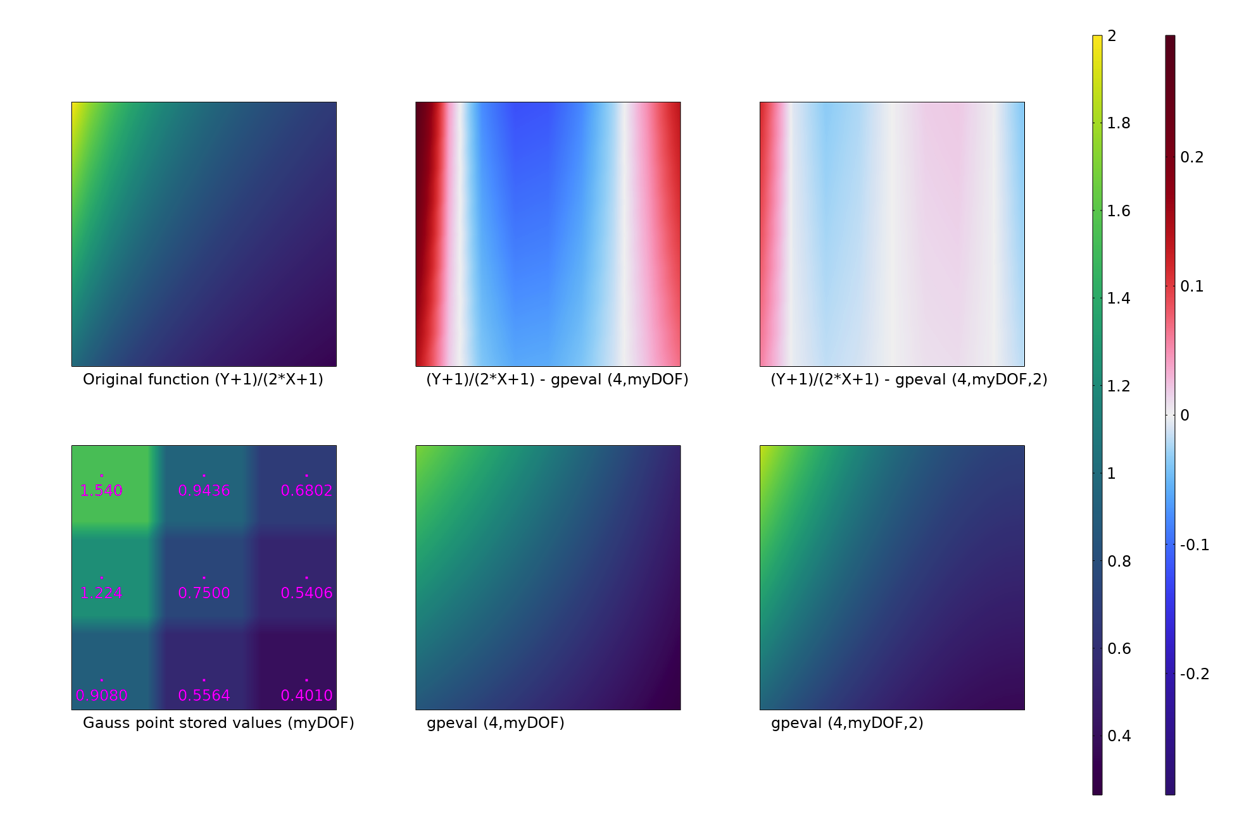
Différents types d’évaluations de données définies aux points de Gauss.
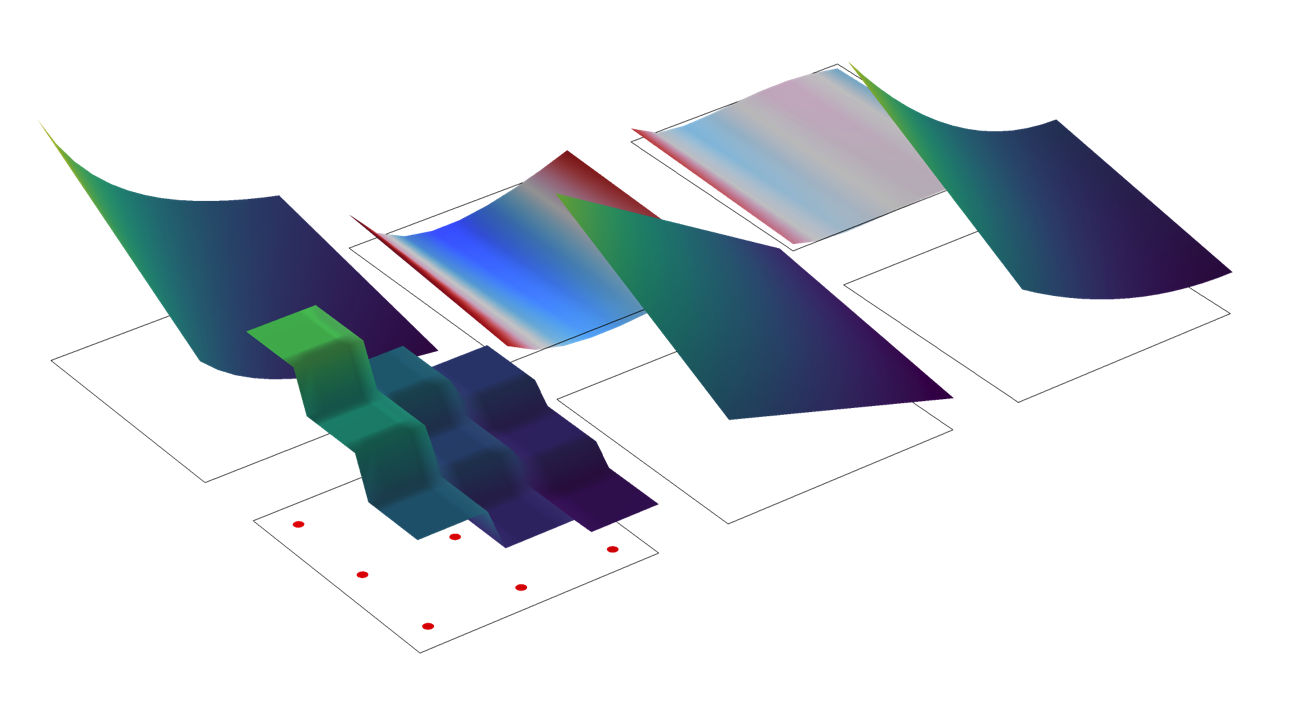
Les mêmes données, représentées par un graphique en élévation.
Le graphique situé en haut à gauche montre la fonction d’origine. En dessous, le comportement d’un graphique de surface de l’état stocké, myDOF, est illustré. Dans le même graphique, on fait apparaître les emplacements des points de Gauss et les valeurs qui y sont stockées. Le comportement par défaut, selon lequel les états des points de Gauss sont représentés par la valeur du point de Gauss le plus proche, est clairement visible. Une bien meilleure approche dans ce cas consiste à évaluer un champ lisse, en utilisant l’opérateur gpeval(). C’est ce que montrent les deux graphiques les plus à droite de la rangée inférieure. La différence entre ces deux graphiques est l’ordre polynomial du champ de lissage. Par défaut, un champ bilinéaire est utilisé (graphique en bas au centre). Dans cet exemple, l’ajustement avec un champ quadratique est une meilleure option. Dans les deux graphiques les plus à droite de la rangée supérieure, on affiche la différence entre les champs lissés et la valeur exacte de la fonction.
Enfin, évoquons deux idées fausses couramment rencontrées:
- Si vous évaluez une expression telle que
solid.sxen un point de Gauss, vous obtenez la valeur calculée au point de Gauss. Cependant, une expression telle quesolid.sGpxougpeval(4,solid.sx)évaluée à un point de Gauss ne récupérera pas le résultat stocké à ce point. La raison tient au fait que ces expressions donnent des champs lisses, obtenus par un ajustement aux moindres carrés. Un polynôme ainsi ajusté ne passera pas nécessairement par ses points de données. - Si vous évaluez une expression telle que
gpeval(4,solid.sx)sur une frontière, les valeurs aux points de Gauss prises sur la frontière sont utilisées pour définir le polynôme d’interpolation. Ce n’est probablement pas ce que vous souhaitez lorsque vous utilisez un graphique de surface sur les frontières d’un modèle de mécanique du solide. Heureusement, les quantités prédéfinies telles quesolid.sGpxetsolid.gpeval(solid.sx)se comportent comme prévu: elles utilisent l’interpolation de domaine.
Évaluer les valeurs maximales
Grâce à la boîte à outils présentée ci-dessus, nous pouvons nous attaquer à cette tâche courante qu’est l’évaluation de valeurs maximales. Tout d’abord, il est important de comprendre qu’il n’existe pas de méthode “correcte”. La seule véritable méthode consisterait à effectuer une analyse avec un maillage si fin que les erreurs de discrétisation seraient infimes. Dans la réalité, cela est rarement possible.
Cela dit, il est généralement préférable d’utiliser les résultats interpolés aux points de Gauss, car ils sont moins sujets à des fluctuations aléatoires. Cela ne donne cependant pas toujours de meilleurs résultats (dans le sens de “les plus proches de la réalité”).
Lors de l’exploitation des résultats, plusieurs approches permettent d’obtenir une valeur maximale (cinq d’entre elles sont présentées dans la figure ci-dessous). Vous pouvez consulter la valeur maximale dans la légende d’un graphique (voir (1) dans la figure ci-dessous) ou vous pouvez ajouter:
- Un sous-noeud Marqueur, par exemple, à un graphique de volume (voir (2)).
- Le sous-noeud Marqueur est évalué à partir des mêmes données que le graphique lui-même, les résultats seront donc toujours cohérents.
- L’évaluation est contrôlée par les réglages de la section Qualité du graphique.
- Un noeud tel que Max/Min en surface dans un groupe de graphiques (voir (3)).
- Ces noeuds ont leurs propres réglages.
- L’évaluation est paramétrée dans la section Avancé.
- Une quantité dérivée de type Maximum sur surface (voir (4)).
- Ces noeuds ont leurs propres réglages.
- L’évaluation est contrôlée dans la section Configuration.
- Un opérateur de type Maximum dans les Définitions du composant (voir (5)).
- Ces opérateurs possèdent leurs propres réglages.
- L’évaluation est paramétrée dans la section Avancé.
- L’opérateur peut être utilisé dans une Evaluation globale.
- Une Marqueur de graphique à un Graphique sur ligne.
- Le marqueur est évalué à partir des mêmes données que le graphique lui-même, les résultats seront donc toujours cohérents.
- Il est contrôlé par les réglages de la section Qualité du graphique.
- Une Evaluation ponctuelle sous le noeud Quantités dérivées lorsque la position du maximum est connue.
- Un point géométrique utilisera une moyenne calculée à partir des arêtes, des frontières ou des domaines adjacents.
- Un point défini par un jeu de données de type Point en 3D prendra sa valeur à partir d’une seule évaluation à l’intérieur d’un seul élément.
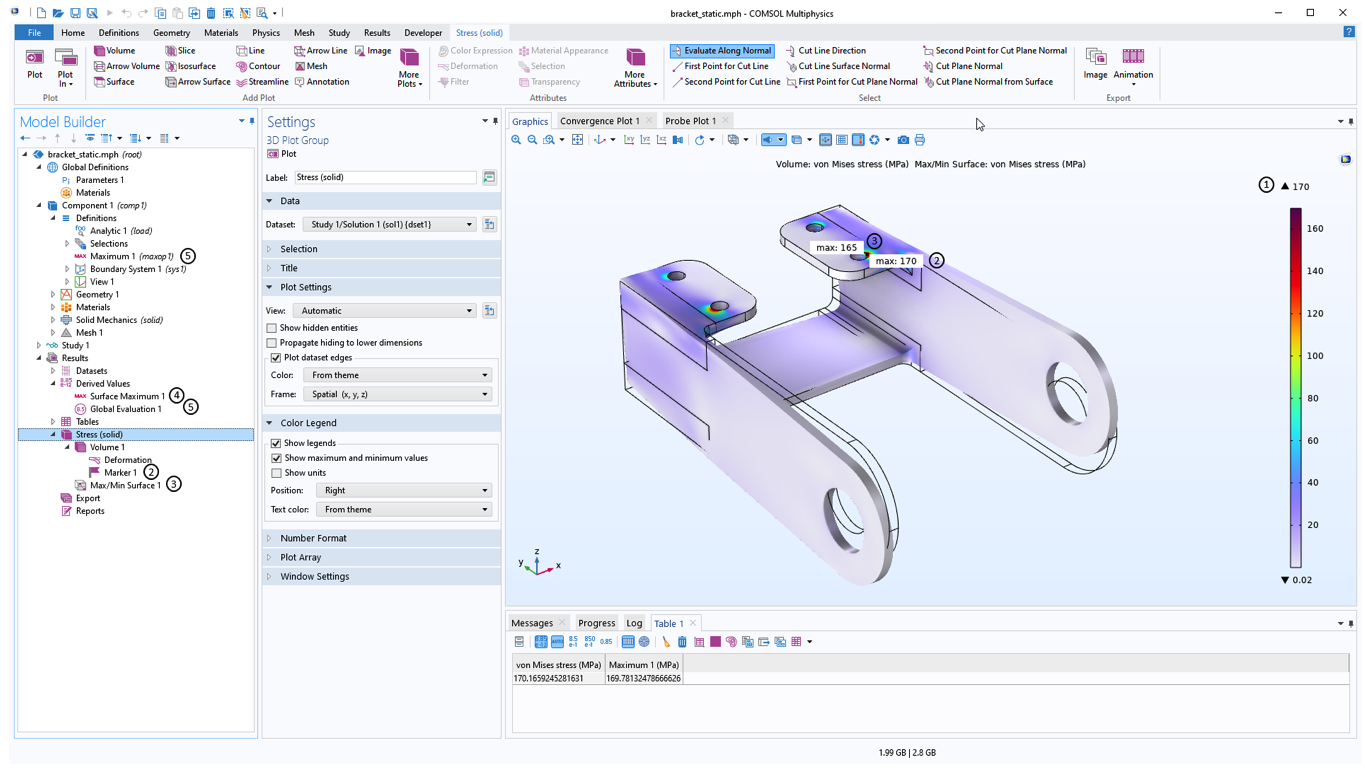
Quelques exemples d’évaluations de la valeur maximale.
Il est évident que les valeurs que vous obtenez en utilisant ces approches ne sont pas nécessairement les mêmes. Quelques conseils:
- Si vous souhaitez mettre en évidence la valeur maximale dans un graphique, utilisez le sous-noeud Marqueur correspondant. Des valeurs incohérentes pourraient prêter à confusion.
- Si vous souhaitez obtenir la valeur la plus défavorable, utilisez une évaluation sans lissage.
- L’évaluation du maximum en surface et en volume peut ne pas donner la même valeur, même si le maximum attendu se trouve à la surface, dès lors qu’un lissage est utilisé ou que le calcul des contraintes implique des états stockés aux points de Gauss.
- Pour les problèmes de mécanique des structures, les contraintes maximales apparaissent souvent sur les frontières. Si la frontière en question n’est pas soumise à un chargement, il existe une astuce intéressante pour obtenir des résultats précis: ajouter une membrane très fine sur cette frontière, avec les mêmes données matériaux que le solide. Cette membrane agira comme une sorte de jauge virtuelle de contrainte. Dans la version 6.1, la fonctionnalité Couche mince a été ajoutée à l’interface de Mécanique du solide. Elle peut être utilisée dans le même but.
Le graphique ci-dessous montre les effets de différentes options pour évaluer le minimum d’une composante de contrainte, en utilisant un marqueur sur des graphiques de surface et de volume. Les variables solid.sy et solid.sGpy sont affichées avec et sans lissage. Comme prévu, chaque valeur calculée sans lissage est plus élevée que la valeur correspondante avec lissage. On peut également noter que, sans lissage, les évaluations de surface et de volume donnent le même résultat. C’est compréhensible, puisque l’extremum est situé sur la surface, et sera donc évalué au même endroit.
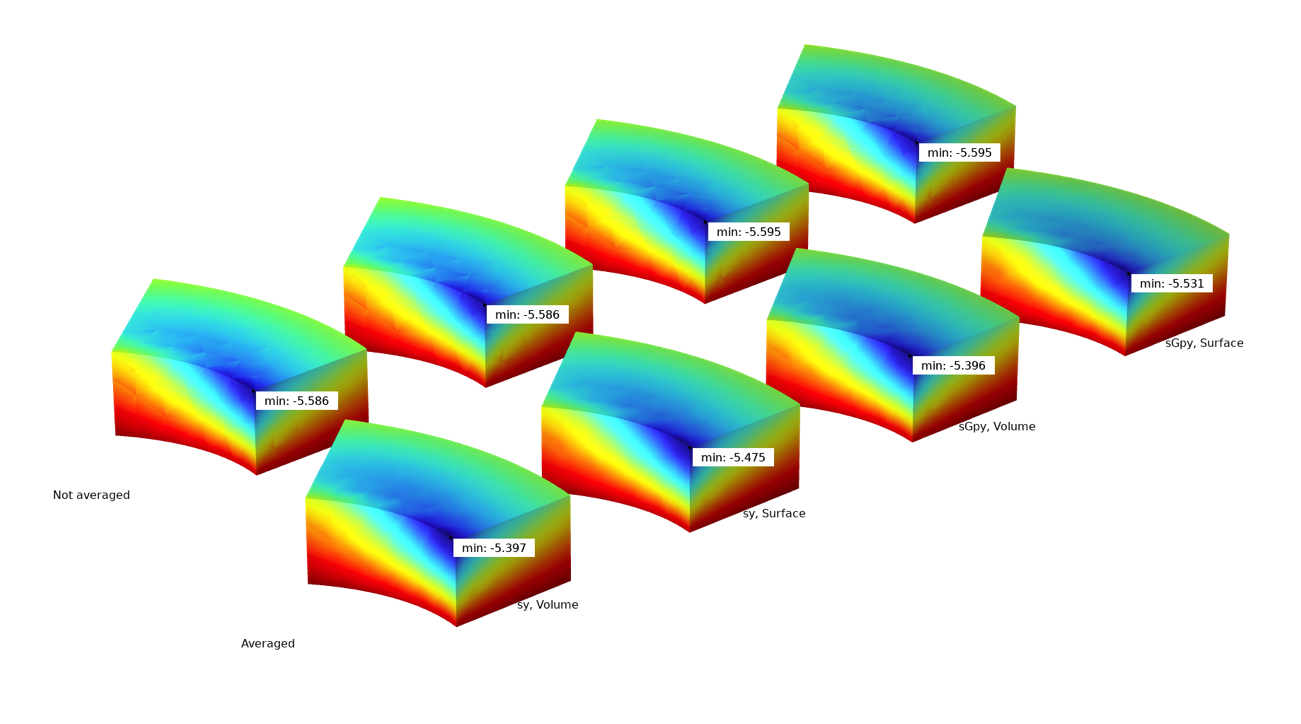
Les effets de différentes options d’évaluation.
Quels résultats de contrainte devrais-je afficher ?
Lorsque vous sélectionnez des résultats à afficher, vous accédez à un menu tel que celui présenté ci-dessous:
Sélection des résultats de contrainte.
Les choix exacts disponibles dépendront de l’interface physique, des lois de comportement des matériaux et d’autres options utilisées. Cela peut sembler impressionnant, mais certaines quantités sont plus importantes que d’autres.
Pour les matériaux isotropes, il est plus courant d’utiliser des mesures de contraintes scalaires, comme les contraintes équivalentes de von Mises ou de Tresca. La contrainte de von Mises est populaire parce qu’elle est facile à évaluer et qu’il est aisé de calculer, par exemple, sa sensibilité. Cependant, la contrainte de Tresca est un choix plus judicieux si l’on préfère jouer la carte de la prudence. La valeur de la contrainte équivalente de Tresca est entre 0 et 17% plus grande que la valeur de la contrainte de von Mises pour un état de contrainte donné. Dans certains domaines de l’ingénierie, comme la conception des réservoirs sous pression, la contrainte de Tresca est toujours utilisée, et parfois appelée intensité de la contrainte.
Même si les contraintes équivalentes de von Mises et de Tresca sont très utiles pour obtenir une vue d’ensemble de l’état de contrainte, elles ne doivent être utilisées que pour évaluer le risque de rupture ou pour trouver le “point de chargement maximal” pour des classes spécifiques de matériaux. Ces mesures de contrainte ont été conçues à l’origine pour prédire la déformation des métaux, et elles sont insensibles à la contrainte moyenne. En effet, un métal n’est pas plus susceptible de casser au fond de la fosse des Mariannes qu’il ne l’est à l’air libre ! La rupture de matériaux tels que les sols ou le béton, en revanche, dépend fortement de la contrainte moyenne ; un état de compression est stabilisant.
Peut-être vous demandez-vous maintenant: comment puis-je produire un graphique où le point chaud est le point critique si mon matériau n’est pas un métal ? La réponse se divise en deux parties: premièrement, vous ne pouvez généralement pas le faire sans introduire des propriétés matériaux décrivant la défaillance. Une fois que vous avez accès à ces valeurs, vous pouvez utiliser le noeud Safety dans les interfaces de mécanique des structures. Avec cette fonctionnalité, différents types de mesures de la marge de sécurité peuvent être utilisés pour de nombreuses classes de matériaux. Comme ces critères sont souvent basés sur les contraintes, tout ce qui a été dit plus haut sur l’évaluation des contraintes s’applique également ici.
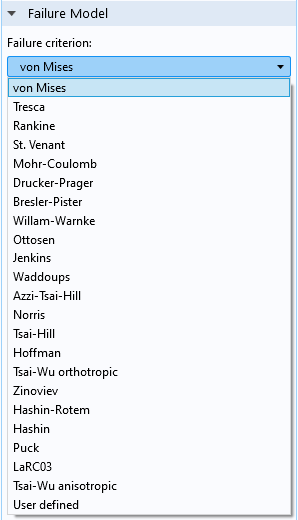
Modèles de rupture de la fonctionnalité Safety.
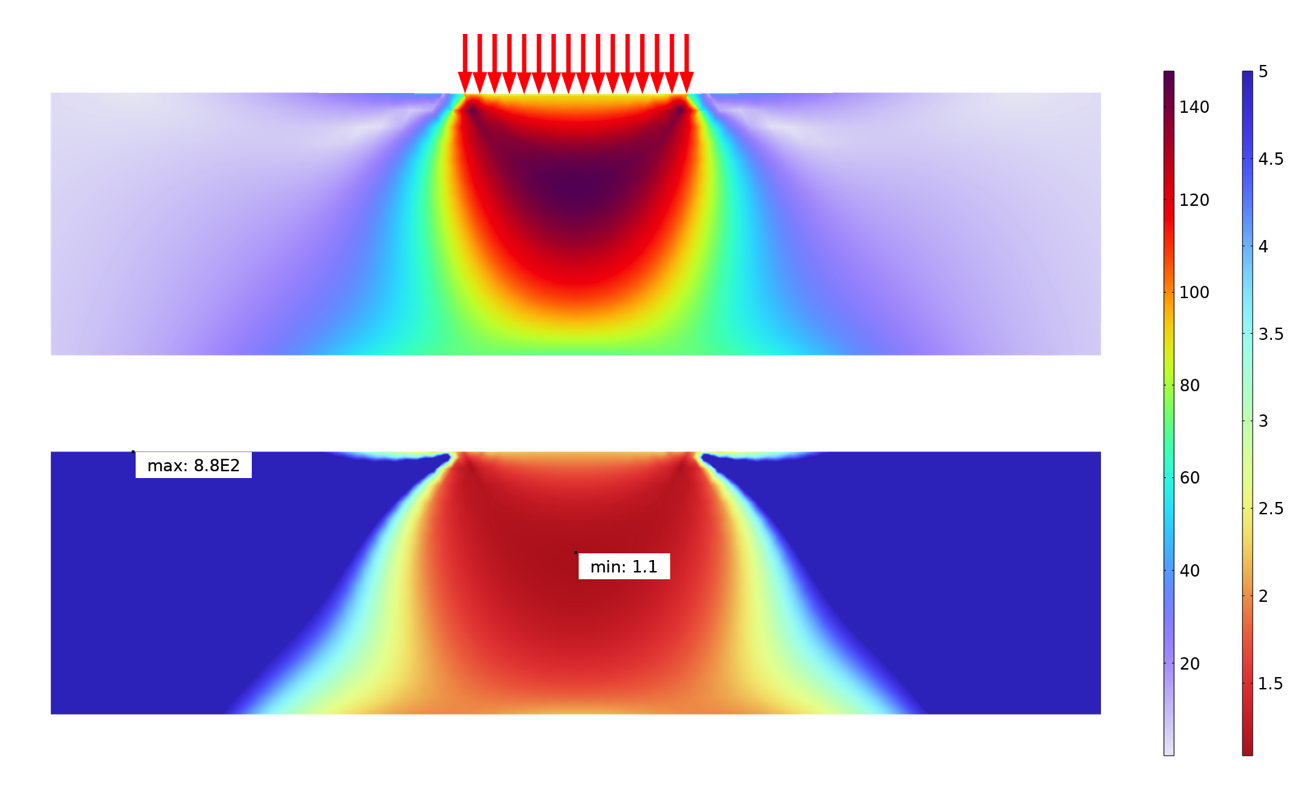
Analyse de la contrainte de von Mises (en haut) et du facteur de sécurité (en bas) d’un problème de mécanique des sols. Le facteur de sécurité utilise un critère de Drucker–Prager.
Il arrive que l’on veuille étudier les différentes composantes de la contrainte, parce que le matériau est anisotrope par exemple, ou que l’on souhaite simplement mieux comprendre la répartition des contraintes. Dans ce dernier cas, il est souvent utile de représenter également les contraintes principales.
Lorsque l’on travaille avec des composantes de contrainte individuelles, il est courant de vouloir les évaluer dans d’autres directions que celles du système de coordonnées global. Plusieurs types de résultats sont étiquetés “système de coordonnées locales”. Cela signifie que l’orientation est déterminée par la sélection du repère dans le noeud de la loi de comportement, comme par exemple Matériau élastique linéaire.
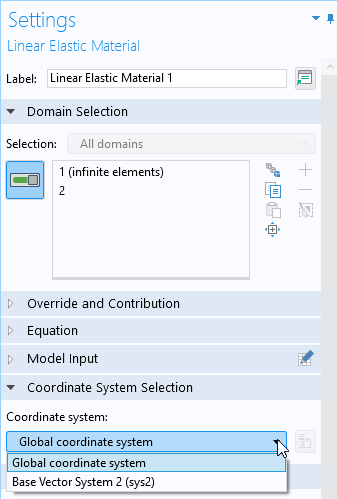
Sélection d’un repère dans une loi de comportement matériau.
Pour un matériau isotrope, la sélection du repère a pour seul effet de définir les directions locales des résultats. Pour les matériaux anisotropes, le principal objectif de la sélection est de fournir les orientations de référence pour les propriétés du matériau. Par ailleurs, vous obtenez des résultats de contraintes et de déformations exprimés selon des directions locales. Dans la version 6.1, une nouvelle fonctionnalité appelée Résultats dans le système local a été ajoutée. Cette dernière permet d’attribuer n’importe quel système de coordonnées locales aux domaines sélectionnés afin de créer des variables contenant, par exemple, des tenseurs de contraintes et de déformations définis selon des orientations locales.
Dans COMSOL Multiphysics®, il existe trois types de tenseurs des contraintes: le tenseur de Cauchy, le premier tenseur de Piola–Kirchhoff et le second tenseur de Piola–Kirchhoff. Pour en savoir plus à ce sujet, vous pouvez consulter notre article de blog “Pourquoi toutes ces contraintes et déformations?” et notre page Multiphysics Cyclopedia sur les contraintes et les équations de mouvement. Si vous envisagez d’étudier une seule composante d’un tenseur des contraintes, les différences peuvent être importantes, mais pour une analyse géométriquement linéaire, tous ces tenseurs sont identiques.
Conclusion
COMSOL Multiphysics® propose une multitude d’options pour affiner l’évaluation et la visualisation des résultats. Pour tirer le meilleur parti de votre simulation, il est important que vous vous familiarisiez avec ces options. Le choix optimal dépendra de l’objet de l’étude et de l’objectif de l’analyse.
Un point qui n’a pas été abordé ici est la manière de composer avec les fortes contraintes qui apparaissent dans les coins ou autres singularités. L’effet des singularités est abordé dans notre article de blog “Singularités dans les modèles éléments finis: Comment gérer les points chauds”. Nous reviendrons probablement sur ce sujet d’un grand intérêt pratique.
Prochaine étape
Vous souhaitez en savoir plus sur les capacités d’analyse des contraintes du logiciel ? Contactez COMSOL en cliquant sur le bouton ci-dessous !




Commentaires (0)