Comment estimer les paramètres des lois de comportement non linéaires dans COMSOL Multiphysics®
Les systèmes mécaniques comportent souvent des matériaux présentant un comportement non linéaire. On peut citer comme exemples les grandes déformations élastiques des joints d’étanchéité, la dépendance à la vitesse de déformation et l’hystérésis pendant la charge cyclique des caoutchoucs et des tissus biologiques mous, ainsi que l’élastoplasticité et le fluage dans les métaux. Grâce au module Nonlinear Structural Materials, le logiciel COMSOL Multiphysics® propose plus d’une centaine de lois de comportement intégrées qui peuvent être utilisées pour modéliser le comportement de matériaux complexes. Toutefois, un inconvénient de ces modèles – souvent phénoménologiques – est qu’ils peuvent faire intervenir un grand nombre de paramètres matériaux, qui doivent être ajustés spécifiquement pour chaque matériau afin que la modélisation fournisse des prédictions précises. Dans cet article de blog, nous montrerons comment ces paramètres peuvent être estimés à partir de données expérimentales issues d’essais mécaniques classiques, en utilisant des techniques de minimisation par moindres carrés non linéaires.
Essais mécaniques classiques
Le point de départ de l’estimation de paramètres matériaux est l’obtention de données expérimentales adéquates. La pertinence de ces données dépend en grande partie du type de matériau et des chargements attendus dans l’application finale, comme nous l’avons vu dans un précédent article de blog. Par exemple, un matériau élastique linéaire isotrope peut être caractérisé par un seul essai uniaxial. Les matériaux présentant une dépendance à la vitesse de déformation et à l’historique de chargement nécessiteront d’autres expériences, telles que des essais de relaxation, de fluage ou des essais cycliques à différentes vitesses de déformation. Si la pièce est soumise à des températures élevées et/ou variables, il peut être nécessaire de tenir compte de la dépendance des propriétés matériaux à la température.
Pour les matériaux subissant de grandes déformations, il est également important de tester le matériau sous différents états de contrainte, même si le comportement du matériau est isotrope. Même s’il peut être tentant d’étalonner un modèle hyperélastique sur la base d’un seul essai uniaxial, comme pour l’élasticité linéaire, la prédiction d’un tel modèle sous chargement compressif ou biaxial peut donner lieu à un comportement inattendu, voire instable, du matériau. Ainsi, pour calibrer les matériaux de type élastomère, on combine couramment des essais de traction uniaxiale, de cisaillement pur et de traction équibiaxiale. On trouvera ci-dessous des exemples de tels essais réalisés avec des échantillons de couches minces de caoutchouc.
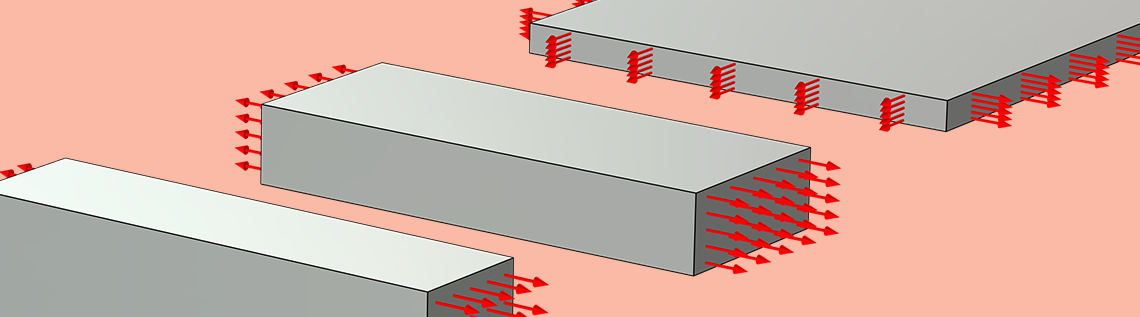
De gauche à droite : essais de traction uniaxiale, de cisaillement pur et de gonflement équibiaxial sur une couche mince de caoutchouc. Les flèches rouges indiquent le déplacement imposé et, pour l’essai de gonflement, la pression appliquée.
Pour des rapports d’aspect d’échantillon bien choisis, les configurations présentées ci-dessus donnent lieu à des états de contrainte et de déformation homogènes au centre des échantillons. Ceux-ci peuvent être estimés à partir de quantités mesurables, telles que les déplacements appliqués et les forces de réaction, ou la pression appliquée et le rayon de courbure de la membrane gonflée. Les essais mécaniques donnant lieu à des états de contrainte et de déformation homogènes sont tout particulièrement adaptés à l’estimation de paramètres, car ils peuvent être modélisés à l’aide d’un seul élément, ce qui réduit considérablement le coût de calcul.
De gauche à droite: cas de chargement homogènes équivalents de traction uniaxiale, cisaillement pur et traction équibiaxiale.
Estimation de paramètres par la méthode des moindres carrés non linéaires
Disposant de données expérimentales et ayant choisi une loi de comportement, nous devons maintenant sélectionner un algorithme d’optimisation qui comparera la prédiction du modèle aux données et actualisera les propriétés matériaux afin de minimiser les écarts. La détermination des paramètres inconnus du matériau, \mathbf{q}^*, correspond donc à la résolution d’un problème dit inverse. Mathématiquement, nous formulons cela comme un problème de moindres carrés pondérés,
où \mathbf{W} est une matrice de coefficients de pondération et \mathbf{r} désigne le vecteur de résidus, qui contient la différence entre les prédictions du modèle, \mathbf{y}, et les données expérimentales \hat{\mathbf{y}}. La prédiction du modèle peut dépendre tant explicitement qu’implicitement des paramètres matériaux, autrement dit, \mathbf{y} = \mathbf{y}(\mathbf{u}(\mathbf{q}), \mathbf{q}), où \mathbf{u} est la solution du problème direct.
Pour mieux illustrer les différentes composantes du problème de moindres carrés, la forme quadratique peut être exprimée de la manière suivante:
Ici, N est le nombre d’ensembles de données ; Q_n et M_n représentent l’erreur de moindres carrés et le nombre de points de données de l’ensemble de données n, respectivement; et P_n(\mathbf{q}; \lambda_m) et \hat{P}_{n,m} désignent respectivement les prédictions du modèle et les données expérimentales. Le paramètre \lambda_m correspond à la variable indépendante de l’expérience, telle que le temps ou l’allongement imposé. Par ailleurs, nous avons supposé que \mathbf{W} est une matrice diagonale de composantes 1/s_{n,m}^2, où s_{n,m} sont des facteurs d’échelle qui pondèrent les différents points et ensembles de données et garantissent que l’objectif est adimensionnel. Le problème des moindres carrés peut également être accompagné de bornes inférieures et supérieures sur les paramètres, qui peuvent être utilisées pour exclure les régions non physiques de l’espace des paramètres dans lesquelles la loi de comportement est instable.
Dans COMSOL Multiphysics®, plusieurs algorithmes d’optimisation sont disponibles pour résoudre les problèmes de moindres carrés. Dans la plupart des cas, l’objectif est une fonction régulière des paramètres et le problème peut être résolu efficacement à l’aide de l’algorithme de Levenberg–Marquardt basé sur le gradient. Pour résumer, la méthode de Levenberg–Marquardt met à jour itérativement les paramètres en alternant de manière adaptative entre une étape de mise à jour dans la direction de descente du gradient lorsque le minimum est éloigné et une étape de Gauss–Newton lorsque le minimum est plus proche et qu’une convergence quasi-quadratique peut être obtenue. Une grandeur essentielle dans l’algorithme de mise à jour est le Jacobien
qui mesure la sensibilité de la prédiction du modèle aux changements des paramètres matériaux. L’évaluation du jacobien peut, en principe, être effectuée analytiquement dans le solveur d’optimisation ; cependant, si le problème est hautement non linéaire et que le modèle direct est peu coûteux à évaluer, une approximation du jacobien par différence finie peut souvent être préférable en matière de robustesse et d’efficacité. Lorsque le jacobien ne peut pas être calculé correctement – par exemple, si l’objectif est non différentiable – l’algorithme BOBYQA (Bound Optimization By Quadratic Approximation) sans gradient est une alternative qui ne nécessite pas le calcul explicite des dérivées.
Si besoin, le solveur Levenberg–Marquardt de COMSOL Multiphysics® peut également calculer les intervalles de confiance ainsi que la matrice de covariance complète en tant que mesures de l’incertitude des paramètres estimés. Cela peut être particulièrement utile si les données expérimentales présentent une variance que vous souhaitez propager aux paramètres matériaux. Pour plus d’informations, vous pouvez consulter le tutoriel Parameter Estimation with Covariance Analysis.
Exemples d’estimation des paramètres de matériaux non linéaires
Dans un précédent article de blog, nous avons vu comment estimer les paramètres matériaux de lois hyperélastiques à l’aide d’expressions analytiques des courbes contrainte-déformation obtenues pour deux cas de chargement courants. Cependant, cette approche ne peut être facilement étendue aux modèles de matériaux inélastiques, pour lesquels il n’existe souvent pas de solutions analytiques explicites. À la place, nous pouvons exploiter les lois de comportement disponibles dans COMSOL Multiphysics®. Nous allons illustrer cette approche à travers deux cas : l’hyperélasticité et la viscoplasticité en grande déformation.
Estimation des paramètres d’un modèle hyperélastique d’Ogden
Dans le premier exemple, nous ajusterons un modèle hyperélastique d’Ogden à des données de tension uniaxiale, de cisaillement pur et de tension équibiaxiale représentatives d’un élastomère souple. Les données sont présentées ci-dessous.

Données de tension uniaxiale, de cisaillement pur et de tension équibiaxiale représentatives d’un élastomère souple. Notez que la contrainte équibiaxiale est beaucoup plus importante et qu’elle est donc représentée sur un second axe des ordonnées.
Nous supposons que l’élastomère est incompressible, de sorte que la densité d’énergie de déformation dans le modèle d’Ogden s’écrit
Ici, deux termes de la fonction de densité d’énergie de déformation sont pris en compte, de sorte que le problème consiste à résoudre les quatre paramètres inconnus du matériau \mathbf{q} = (\mu_1, \alpha_1, \mu_2, \alpha_2), comme on peut le voir dans la figure ci-dessous.
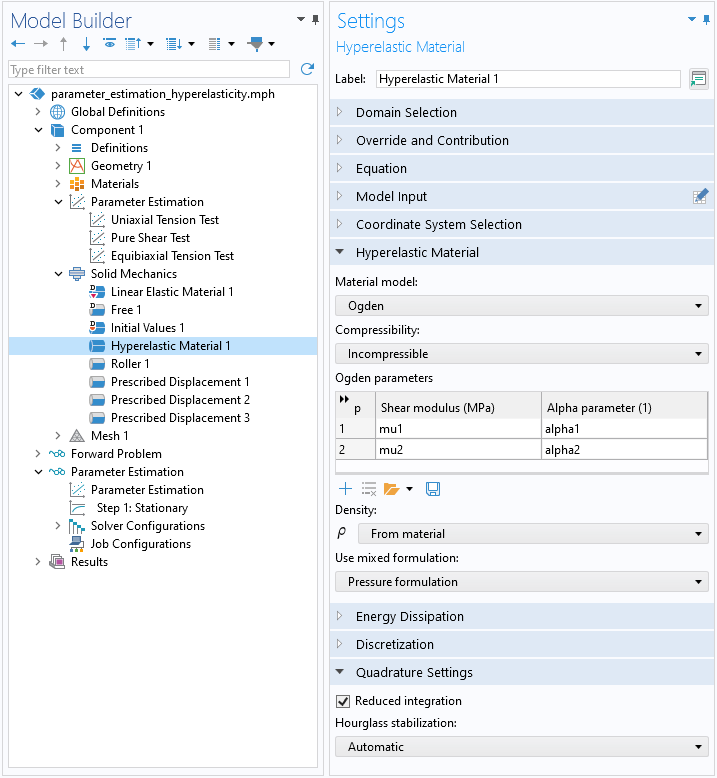
Réglages du modèle incompressible d’Ogden avec deux termes. Les cas de chargement étant homogènes, notez que l’intégration réduite peut être utilisée pour réduire le coût de calcul.
Après avoir mis en place la loi de comportement, nous pouvons importer les ensembles de données dans des tables de résultats et les relier aux expressions correspondantes du modèle à l’aide de la fonctionnalité Objectif global par moindres carrés. La figure ci-dessous montre les réglages de l’objectif par moindres carrés constitué à partir des données uniaxiales. La variable comp1.P_ua, utilisée dans le champ Expression du modèle, est définie comme étant la moyenne volumique de la variable prédéfinie pour la contrainte nominale, solid.PxX.

Les réglages de l’objectif global par moindres carrés associés aux données de tension uniaxiale.
Dans l’étape Estimation de paramètres de l’étude, nous ajoutons les trois objectifs et spécifions les paramètres matériaux à estimer. Dans la table Estimated Parameters, mu1 et alpha1 sont définis positifs, tandis que mu2 et alpha2 sont définis négatifs. Ces contraintes garantissent que la loi de comportement répond aux critères de stabilité connus, à savoir \mu_p\alpha_p > 0 pour le modèle d’Ogden.

Les paramètres de l’étape Estimation de paramètres.
La progression de la solution peut être suivie pour chaque itération du solveur d’optimisation dans un graphique qui compare la prédiction courante du modèle avec les données expérimentales. Comme le montre l’animation ci-dessous, l’algorithme de Levenberg–Marquardt améliore rapidement la prédiction du modèle uniaxial et de cisaillement pur et, après quelques itérations supplémentaires, la réponse équibiaxiale fortement non linéaire.
Estimation des paramètres d’un modèle viscoplastique de Bergstrom–Boyce
Dans l’exemple suivant, nous considérons le modèle plus complexe de Bergstrom–Boyce pour les polymères viscoplastiques, qui présente à la fois une vitesse de déformation, un historique de chargement et un comportement dépendant de la température. Nous présentons ci-dessous des courbes de contrainte–déformation représentatives d’essais cycliques de traction et de compression uniaxiales réalisés à deux vitesses de déformation différentes et à température ambiante.
Courbes de charge–décharge en traction et compression uniaxiales à deux vitesses de déformation différentes (0,1%/s et 10%/s) pour un modèle représentatif d’un matériau polymère viscoplastique.
Le modèle de Bergstrom–Boyce est disponible dans la version 6.2 de COMSOL Multiphysics® en ajoutant le sous-noeud Viscoplasticité de polymère à la loi de comportement Matérau hyperélastique. Ici, le modèle hyperélastique parent définit un réseau élastique à l’équilibre, tandis que le sous-noeud ajoute un réseau parallèle hors équilibre contenant à la fois un élément élastique et un élément inélastique. Dans cet exemple, nous modélisons les éléments élastiques avec une densité d’énergie de déformation d’Arruda–Boyce quasi-incompressible, et nous incluons à la fois l’écrouissage et le durcissement par contrainte dans l’écoulement viscoplastique. Au total, la loi de comportement fait intervenir six paramètres matériaux indépendants, \mathbf{q} = (\mu_0^\textrm{eq}, N_\textrm{c}, \beta_\textrm{v}, A, c, n): le module de cisaillement du réseau à l’équilibre, \mu_0^\textrm{eq}; le nombre de segments de la chaîne, N_\textrm{c}; le facteur d’énergie entre le réseau hors équilibre et le réseau à l’équilibre, \beta_\textrm{v}; le coefficient de taux de viscoplasticité, A; l’exposant de déformation, c; et l’exposant des contraintes, n.

Réglages de la loi de Bergstrom–Boyce dans la fonctionnalité Viscoplasticité de polymère. La fenêtre Graphiques montre des modèles à élément unique pour les essais de compression et de traction uniaxiaux.
Le problème des moindres carrés peut maintenant être configuré et résolu de la même manière que pour l’hyperélasticité. Comme le montre l’animation ci-dessous, une solution visuellement satisfaisante est déjà obtenue après environ 5 itérations, même si le solveur d’optimisation a besoin d’environ 12 itérations pour atteindre la convergence. En effet, les critères d’arrêt par défaut du solveur de Levenberg–Marquardt vérifient si l’incrément des paramètres ou l’angle maximal entre le vecteur des résidus et le jacobien est plus petit qu’une tolérance d’optimalité donnée. Dans les paramètres du solveur d’optimisation, vous pouvez éventuellement inclure un critère d’arrêt supplémentaire basé sur le changement relatif du vecteur résidu, ce qui peut être utile si le solveur atteint un minimum local relativement plat dans l’espace des paramètres où les améliorations de la fonction objectif sont faibles. Cependant, les critères d’arrêt par défaut sont normalement plus robustes que le critère basé sur la réduction des résidus.
Tester la stabilité de votre loi de comportement
Après avoir estimé les paramètres d’une loi de comportement nonlinéaire, il est bon de la tester pour s’assurer qu’elle est numériquement stable. Ce sujet sera traité en détail dans la partie 2 de cette série.
Pour conclure et en apprendre davantage
Dans cet article de blog, nous avons montré comment estimer les paramètres des lois de comportement de matériaux non linéaires dans COMSOL Multiphysics® à partir de données provenant d’essais mécaniques classiques. L’approche présentée est généralement applicable à tout type de loi de comportement et de données d’essais mécaniques.
Pour réaliser vous-même l’estimation des paramètres de différents lois de comportement, en suivant des instructions pas à pas, consultez les exemples suivants de la Bibliothèque d’Applications :




Commentaires (0)