
Comment calculer l’aire de la surface projetée d’un fichier CAO dans COMSOL®?
Vous est-il déjà arrivé de vouloir calculer l’aire de la surface projetée d’un fichier CAO? Cela peut être utile dans de nombreux cas, comme par exemple pour estimer rapidement la traînée aérodynamique. Il existe plusieurs façons de procéder si vous ne vous intéressez qu’à l’aire de la surface projetée selon quelques directions, mais qu’en est-il lorsque vous souhaitez la calculer dans toutes les directions possibles ? Nous examinerons ici une manière efficace de calculer et d’exploiter ce type de données.
Quelques approches simples
Considérons une géométrie CAO complexe et posons-nous la question suivante: quelle est l’aire projetée de cette géométrie le long d’une direction particulière ? Il y a plusieurs façons d’y répondre. Tout d’abord, nous pouvons utiliser l’opérateur de Projection générale. Cette approche nous oblige à dessiner une boîte autour de la géométrie complète et à mailler très finement pour obtenir un résultat précis. De ce fait, et en raison de la nécessité de calculer l’intégrale sur l’ensemble du domaine, cette approche peut se révéler être relativement coûteuse. La seconde approche, qui est une nouveauté de la version 6.0, utilise la fonctionnalité Projection, qui permet de projeter des objets et des entités 3D sur des plans de travail définis au préalable dans la géométrie. Nous pouvons mesurer directement les surfaces de ces projections. Cette approche basée sur la CAO est beaucoup plus rapide et ne s’appuie sur aucun maillage, mais nécessite de disposer du module CAD Import ou du module Design, ou de l’un des LiveLink™. Ces deux approches deviennent fastidieuses lorsque l’on souhaite obtenir l’aire de la surface projetée selon un grand nombre de directions arbitraires.
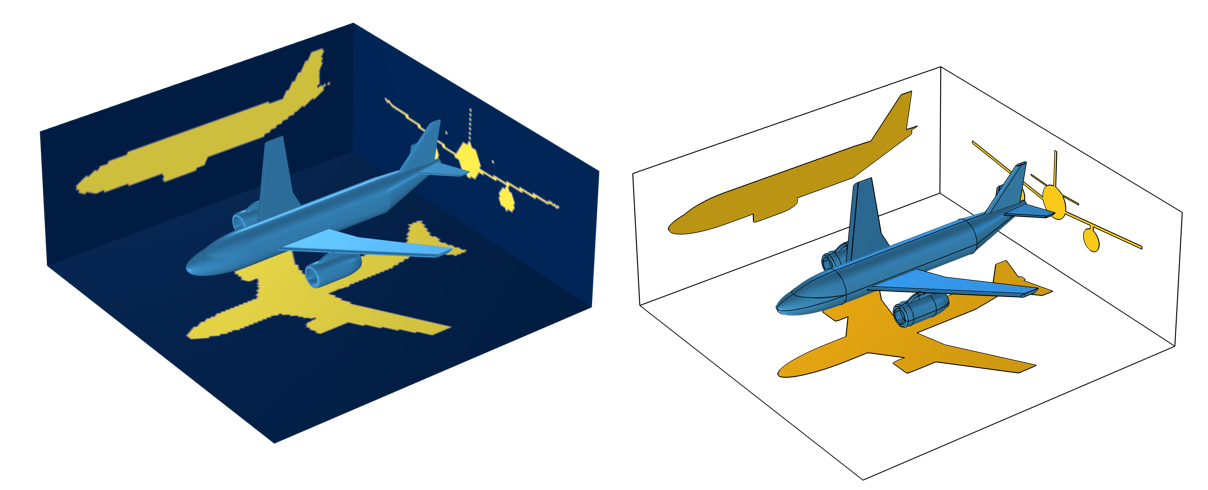
Deux façons de déterminer l’aire de la surface projetée: via un opérateur Projection générale (à gauche), dont les résultats dépendent du maillage, et avec la fonctionnalité Projection qui génère les surfaces projetées sur un ensemble de plans de travail (à droite).
Une approche plus générale
Plutôt que de mailler le volume de la CAO ou d’ajouter des opérations géométriques, nous pouvons exploiter la définition de l’aire projetée, qui est:
où \beta est l’angle entre la ligne de visée et la normale à la surface, pour les surfaces visibles dans cette direction.
Il est aisé de calculer une intégrale de surface, mais comment peut-on évaluer le terme \cos \left( \beta \right) ? Nous pouvons obtenir ce terme via l’interface de Rayonnement de surface à surface, lorsque nous utilisons une source de rayonnement externe de type Distance infinie. Le calcul ne nécessite qu’un maillage de la surface de la pièce, et non du volume. Il n’est pas non plus nécessaire de résoudre le rayonnement de surface à surface, car ce flux externe incident est calculé lors d’une étape de prétraitement en tenant compte des effets d’ombrage. Nous pouvons donc simplement intégrer le flux externe sur toutes les surfaces, diviser par le flux incident nominal, et obtenir l’aire de la surface projetée le long de n’importe quelle direction spécifiée dans la condition Source de rayonnement externe. L’intégrale étant calculée par la méthode de quadrature de Gauss, par défaut d’ordre 4, il est possible d’utiliser un maillage relativement grossier.
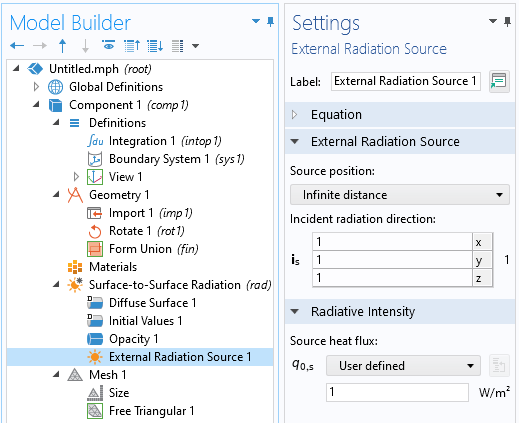
La fonctionnalité Source de rayonnement externe peut être utilisée pour éclairer une géométrie afin d’en calculer l’aire de la surface projetée.
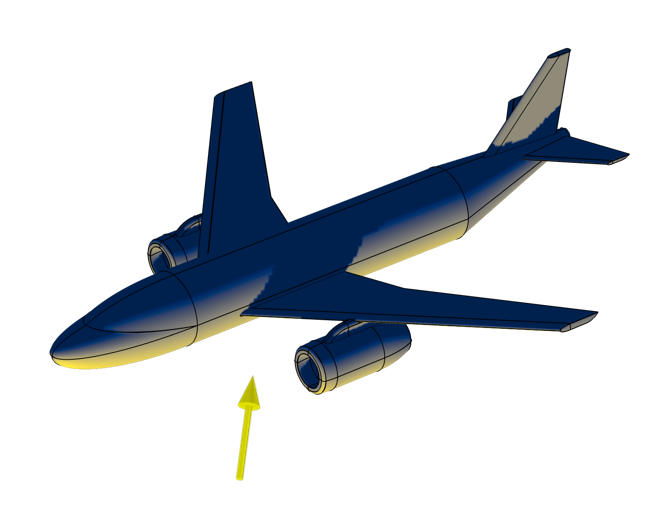
Le flux incident, précalculé par la fonctionnalité Source de rayonnement externe, peut être intégré pour déterminer l’aire projetée de la géométrie. On remarquera l’ombre propre et l’ombre portée de l’aile.
Extraire et exploiter les données relatives à l’aire de la surface projetée dans toutes les directions
Il est souvent nécessaire d’évaluer l’aire de la surface projetée dans toutes les directions. Nous pourrions être tentés de réévaluer l’intégrale ci-dessus pour toute direction incidente d’intérêt, mais cela se révélerait en pratique assez coûteux.
A la place, imaginons une sphère entourant l’objet, et choisissons un nombre fini de directions sur cette sphère à partir desquelles nous éclairerons la cible. Entre ces directions finies, nous pouvons alors utiliser l’interpolation linéaire sur toute la surface de la sphère. Mais avant de choisir ces directions, il convient de remarquer que la surface projetée sera symétrique par rapport à tout plan passant par le centre de la sphère environnante, et que la géométrie avec laquelle nous travaillons ici est symétrique par rapport au plan médian ; il est donc logique d’exploiter ces deux symétries et de ne considérer qu’un quart de sphère situé dans le quadrant xy positif de l’espace.
Nous allons ci-après passer en revue les étapes suivantes:
- Création d’une géométrie exploitant la symétrie de la pièce de CAO, avec un nombre fini de points définissant les directions de projection.
- Calcul de l’aire de la surface projetée le long de ces directions
- Interpolation des données sur toutes les directions intermédiaires
- Utilisation de ces données
Pour commencer, nous créons une géométrie un peu particulière, comme le montre la figure ci-dessous. Cette géométrie qui s’apparente à un maillage de quart de sphère est obtenue en créant d’abord séparément un maillage de quart de sphère unitaire, en exportant ce maillage et en l’important ensuite dans un second Composant du modèle. Les réglages de l’import sont tels que chaque élément du maillage de frontière définit une surface distincte et que chaque noeud se trouve sur un point géométrique. Cette surface se situe dans le quadrant xy positif de l’espace.
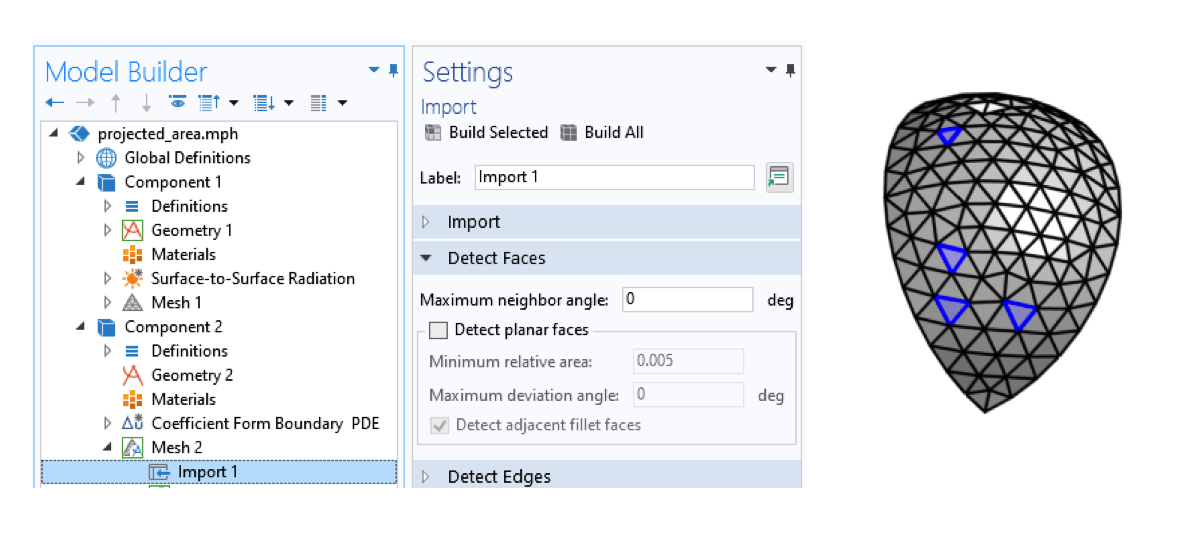
Import d’un maillage avec des réglages permettant d’obtenir une face par élément.
Chacun de ces points représentera l’une des directions échantillonnées pour lesquelles nous évaluerons l’aire de la surface projetée. Sur chaque face triangulaire entre ces points, nous utiliserons une interpolation linéaire, définie par les fonctions de forme des éléments finis, de manière à obtenir une approximation de l’aire projetée pour toute direction incidente.
Pour cela, nous ajoutons une interface EDP, forme coefficient sur frontière que nous appliquons sur l’ensemble des surfaces de notre modèle de quart de sphère. Nous sélectionnons ensuite une discrétisation linéaire et nommons la variable dépendante AREA.
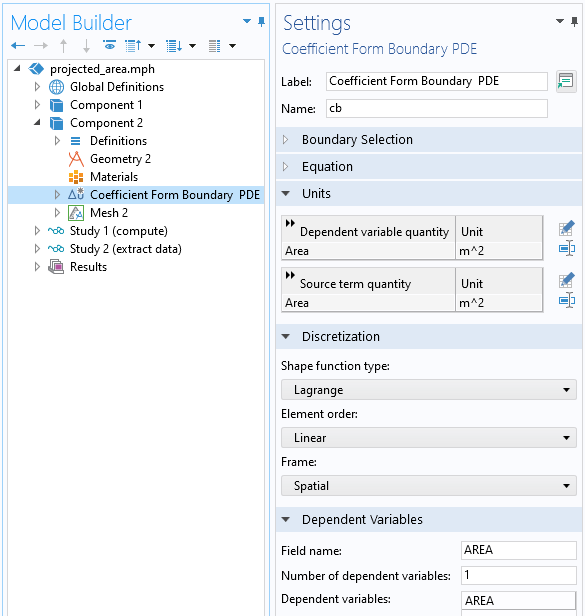
Réglages de l’interface EDP, forme coefficient sur frontière, utilisée pour réaliser l’interpolation.
Dans cette interface, nous appliquons la condition de Contrainte au niveau des points à l’ensemble des points de la géométrie. Cela a pour effet de contraindre entièrement le problème, puisque tous les noeuds se trouvent sur des points de la géométrie. Ainsi, tous les autres réglages physiques de l’interface sont sans effet et peuvent être laissés à leurs valeurs par défaut. La solution obtenue est simplement une interpolation linéaire entre les valeurs nodales imposées sur les sommets de chaque face triangulaire.
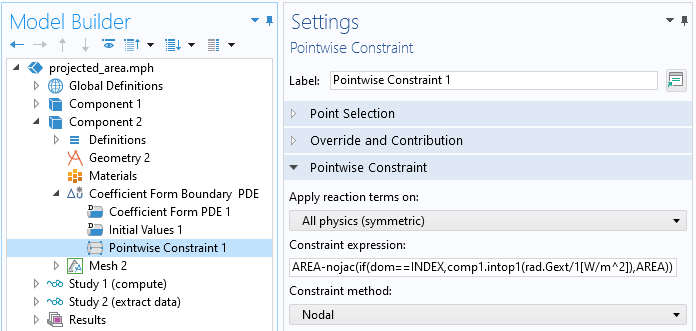
Contrainte au niveau des points, appliquée sur tous les points du modèle.
Nous devons donc définir, en chaque point, l’aire projetée le long de cette direction d’observation particulière. Pour ce faire, nous utilisons l’expression de la contrainte suivante:
AREA-nojac(if(dom==INDEX,comp1.intop1(rad.Gext/1[W/m^2]),AREA))
Examinons de plus près cette expression qui définit la valeur de AREA en chaque point. Tout d’abord, l’expression entière doit être égale à zéro: la variable AREA est donc égale à l’expression contenue dans l’opérateur nojac(). Cet opérateur indique que l’expression qu’il contient n’ajoute aucune contribution au calcul de la jacobienne. Pour plus de détails à ce sujet, vous pouvez consulter notre article de blog sur l’accélération de la convergence des modèles grâce à la dérivation symbolique. L’opérateur nojac() contient ici l’instruction if(logical expression, true, false), dans laquelle on trouve l’expression logique dom==INDEX. En effet, chaque objet géométrique (qu’il s’agisse d’un domaine, d’une frontière, d’une arête ou d’un point) est associé à un nombre entier unique: son indice de domaine, dom. Dans le cadre de l’étude que nous nous apprêtons à réaliser, nous effectuerons un balayage auxiliaire sur le paramètre global INDEX pour tous les points de cette géométrie.
Durant ce balayage, lorsque l’expression logique est évaluée comme étant fausse, la variable AREA reste inchangée. Lorsque l’expression logique est vraie, nous obtenons l’aire projetée, c’est-à-dire l’intégrale du flux intercepté divisé par le flux incident. L’opérateur d’intégration comp1.intop1() est défini dans notre première composante sur toutes les surfaces exposées du fichier CAO. Lorsque cette intégrale est évaluée, afin que la caractéristique Source de rayonnement externe du premier composant puisse connaître la direction associée au point du second composant, nous utilisons une deuxième variable intégrale de couplage, définie sur l’ensemble des points de ce second composant, et l’utilisons pour définir la direction du rayonnement incident de la Source de rayonnement externe:
comp2.intop2(x[1/m]*(dom==INDEX))
Cette expression peut être lue de la manière suivante: on évalue sur tous les points du second composant, la coordonnée x (ou y, ou z), et on multiplie ce résultat par (dom==INDEX), qui sera égal à zéro ou à un. En d’autres termes, on évalue uniquement le vecteur d’éclairage orienté vers le point courant, désigné par l’indice INDEX, comme l’illustre la capture d’écran ci-dessous.
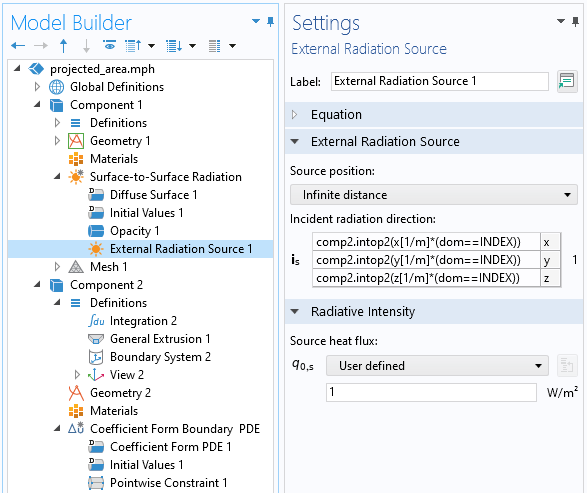
Dans le premier composant, la direction du rayonnement incident est définie par les points de la géométrie du second composant.
Il convient ensuite de balayer toutes les valeurs de notre paramètre d’indice, ce qui est fait par le biais d’une étape Stationnaire comportant un balayage de paramètres auxiliaires. Dans cette étude, nous n’avons pas besoin de résoudre le problème du rayonnement de surface à surface, puisque la mesure du flux incident est une étape de prétraitement.
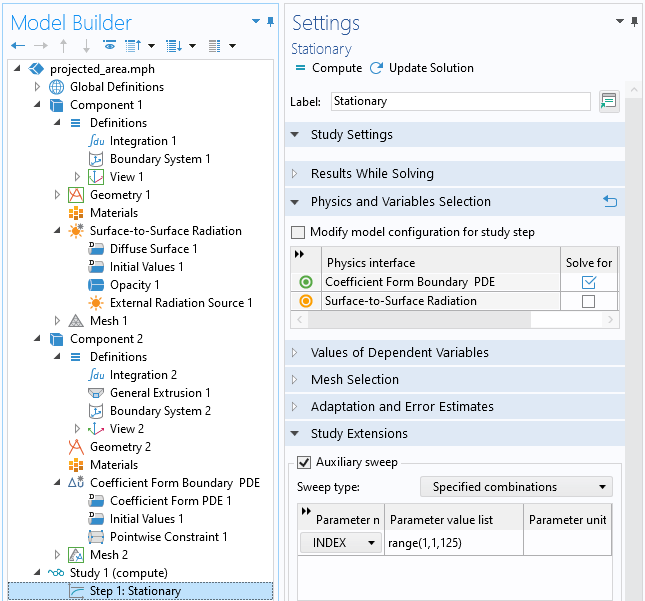
L’aire projetée est obtenue en effectuant un balayage du paramètre d’indice.
Puisque seule la dernière valeur du balayage contient l’ensemble des résultats, nous pouvons conserver uniquement cette dernière solution. Cela peut être fait via l’étape Combiner les solutions, comme le montre la capture d’écran ci-dessous.
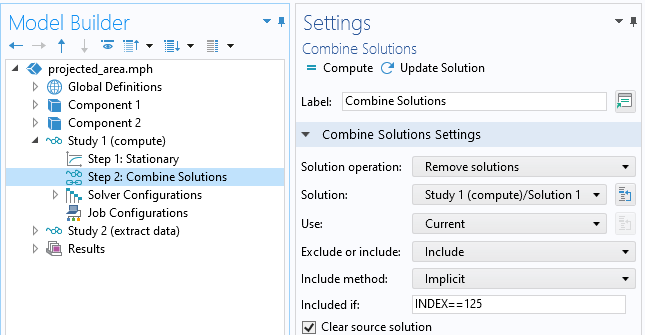
Utilisation de l’étape Combiner les solutions pour ne conserver que la dernière solution du balayage de paramètre.
Afin de montrer comment ces données pourraient être utilisées, nous ajoutons une seconde étude avec une étape Temporelle, au cours de laquelle nous suivrons un point à la surface de la sphère. Nous utilisons pour cela un système de coordonnées sphériques aligné sur l’axe de l’avion, avec la direction verticale orientée vers le haut définissant les angles \phi et \theta.
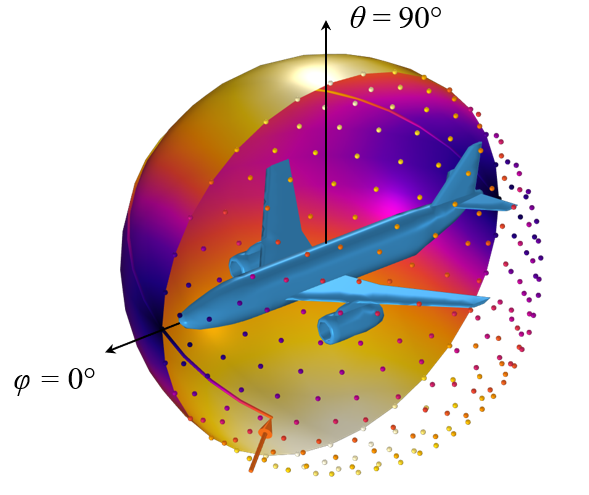
Le modèle CAO et l’aire de sa surface projetée représentée par un ensemble de points pour les directions discrètes, ainsi qu’interpolée sur une surface. La valeur du champ le long d’une ligne tracée sur cette surface peut être évaluée au moyen d’un opérateur d’Extrusion générale en coordonnées sphériques.
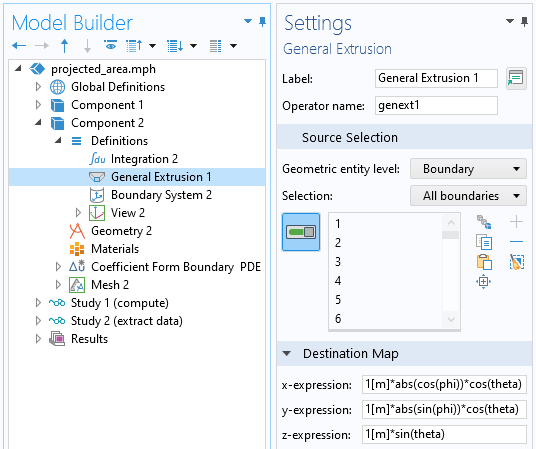
Extraction de l’aire projetée à partir des données interpolées sur la surface via un opérateur d’ Extrusion générale.
Pour extraire des données d’un point arbitraire de cette sphère, en coordonnées sphériques, nous pouvons utiliser l’opérateur Extrusion générale comme une sonde dynamique en spécifiant des variables tenant compte de la symétrie de la solution pour les expressions de la carte de destination.
Conclusions
Il existe plusieurs façons de calculer l’aire de la surface projetée d’un fichier CAO. Parmi les trois méthodes présentées ici, l’utilisation de l’opérateur Projection générale est la plus coûteuse en termes de calculs, car elle repose sur une intégrale de domaine et nécessite un maillage fin dans le domaine environnant. Par conséquent, elle ne doit être utilisée que si les deux autres approches ne peuvent être employées. La seconde approche, qui utilise la fonctionnalité Projection, est une opération basée sur la géométrie. Bien qu’elle soit simple, précise et indépendante du maillage, elle nécessite de spécifier manuellement chaque direction de projection. La dernière approche, qui utilise l’interface Rayonnement de surface à surface, est la plus complexe à mettre en oeuvre mais offre une grande flexibilité dans la réutilisation des données pour une modélisation ultérieure basée sur des équations. Le fichier illustrant cette approche peut être téléchargé ici:




Commentaires (0)