Réponse impulsionnelle acoustique d’une enceinte intelligente à l’intérieur d’une pièce

Récemment sur le blog COMSOL, nous avons détaillé la modélisation acoustique d’une pièce à l’aide d’une approche hybride éléments finis (FEM)–rayons. Dans cet article de blog, nous utiliserons la fonctionnalité de couplage MEF–rayons disponible dans le logiciel COMSOL Multiphysics^® pour modéliser la réponse d’une enceinte intelligente posée sur une table dans une petite pièce. En plus de cette fonctionnalité, nous utiliserons un couplage manuel pour obtenir une description plus détaillée de la source en champ proche. L’approche combine un modèle détaillé par éléments finis du transducteur, ses caractéristiques de rayonnement sur toute la gamme de fréquences, un modèle MEF ondulatoire à basse fréquence et un modèle de rayons acoustiques à haute fréquence. En outre, les propriétés d’absorption d’un plafond suspendu sont définies de façon dépendantes de l’angle et de la fréquence.

Vous recherchez notre article de blog récent sur l’utilisation d’une approche hybride FEM-rayons ? Vous pouvez le consulter ici : “Modeling Room Acoustics Using a Hybrid Approach”. Notez que cet article de blog décrit comment concaténer les bandes de hautes et basses fréquences de la réponse impulsionnelle, mais la concaténation n’est pas abordée explicitement ici.

Formulation du problème

Notre exemple se concentre sur la réponse acoustique d’une enceinte intelligente lorsqu’elle est posée sur une table à l’intérieur d’une petite pièce. La pièce est équipée d’un plafond suspendu (ou “faux plafond”) constitué d’un matériau poreux doublé d’une cavité d’air. Les murs, le canapé et le sol ont également des propriétés d’absorption du son. Un seul récepteur (microphone) a été positionné dans ce modèle. La configuration du problème est illustrée dans l’image ci-dessous.

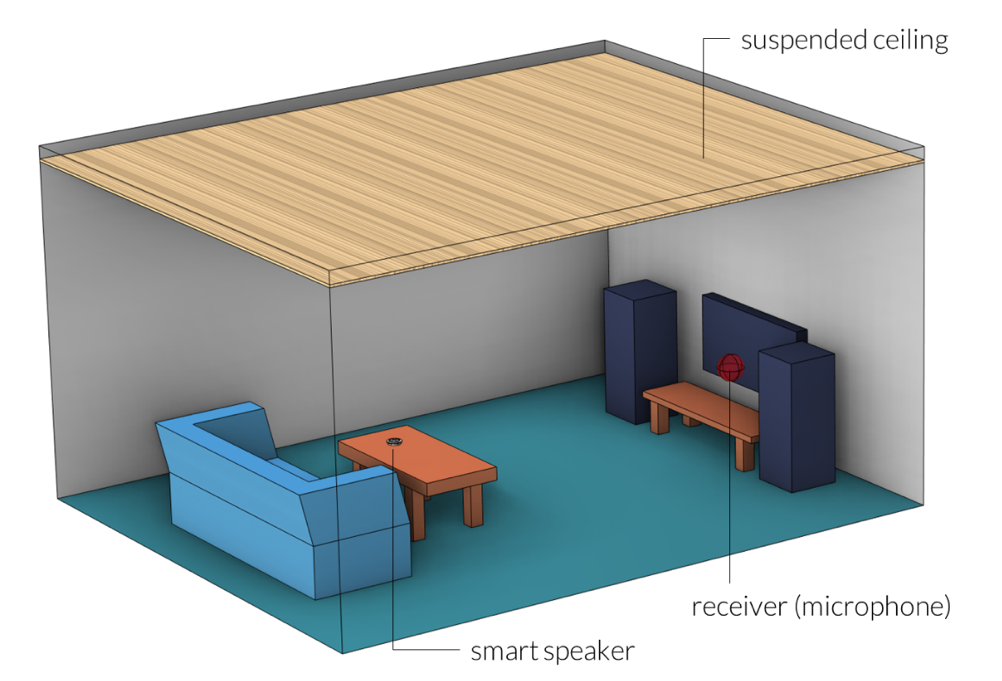
Figure 1. Configuration du problème.

Dans la configuration actuelle, l’enceinte intelligente est modélisée en combinant la pression acoustique avec un système discret de composants électromécaniques (les paramètres Thiele et Small). Le système discret Circuit électrique est couplé avec l’interface Pression acoustique, domaine fréquentiel en utilisant la fonctionnalité Haut-parleur réduit, frontière interne. Pour plus de détails sur cette approche de modélisation, vous pouvez vous référer au tutoriel Lumped Loudspeaker Driver.

Un schéma de l’enceinte intelligente est représenté dans l’image 2 ci-dessous. Le modèle comprend :

• Volumes d’air avant et arrière
• La membrane du haut-parleur (couplé avec le système discret)
• Une grille
• Un évent reliant le volume arrière à l’extérieur
• Les pertes thermovisqueuses de couche limite dans les zones minces et dans les guides d’ondes fins.

La géométrie comprend également trois microphones (représentés par un modèle RCL), bien qu’ils ne soient pas explicitement utilisés dans ce tutoriel. Notez qu’il s’agit d’une géométrie simplifiée qui peut, bien entendu, s’étendre à un modèle multiphysique complet comportant une géométrie et une physique beaucoup plus détaillées.

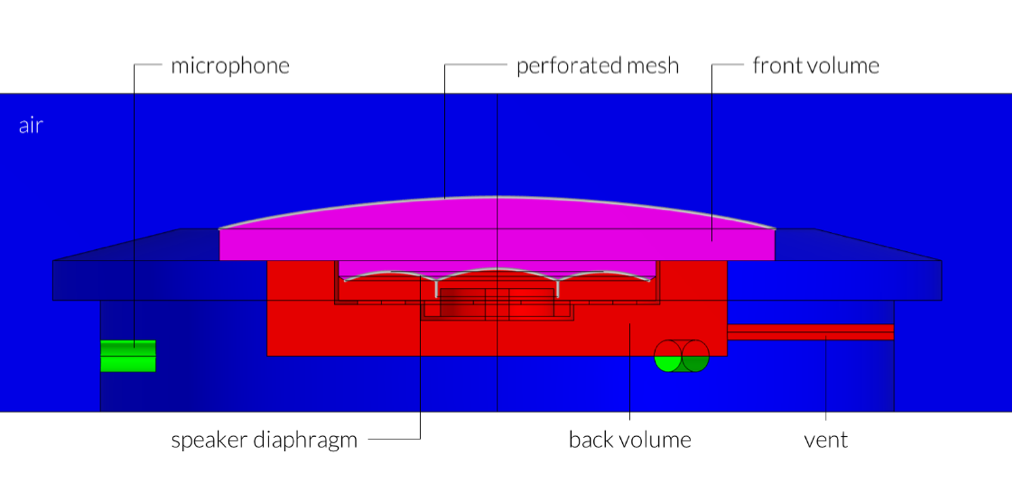
Figure 2. L’enceinte intelligente.

Figure 3. La partie réelle de la pression acoustique sur la surface du haut-parleur à 1 kHz.

Combinaison des méthodes

La configuration du présent modèle est basée sur la combinaison de la précision de l’acoustique ondulatoire, avec l’efficacité de l’acoustique géométrique par lancer de rayons (le cas échéant). Nous montrons ici la configuration nécessaire pour calculer les solutions d’intérêt dans les basses et hautes fréquences. La concaténation de la réponse aux hautes et basses fréquences n’est pas effectuée dans ce modèle, mais découle du modèle présenté dans l’article de blog mentionné précédemment.

Basses fréquences

Pour les basses fréquences, l’acoustique de la pièce et du transducteur sont résolues directement avec l’interface Pression acoustique, domaine fréquentiel et l’interface Circuit électrique. Cela est mis en place dans le Composant 2 du modèle et résolu dans l’Etude 2. Ce dernier est utilisé pour modéliser les composants électromécaniques du transducteur. Le plafond suspendu est modélisé avec la fonctionnalité Poroacoustique. Les pertes thermovisqueuses à l’intérieur du haut-parleur sont prises en compte avec la fonctionnalité Acoustique dans des régions minces pour les structures de guides d’ondes. Pour certaines zones autour de la bobine vocale et de l’aimant, où les pertes sont également importantes, la fonctionnalité Impédance de la couche limite thermovisqueuse est utilisée.

Dans cet exemple, le régime basses fréquences est résolu jusqu’à 1200 Hz. La fréquence maximale résolue peut probablement être augmentée davantage. Pour résoudre efficacement jusqu’à cette fréquence élevée, nous optons pour le solveur itératif suggéré, reposant sur la méthode “shifted Laplace”. Le modèle résout environ 3,8 millions de degrés de liberté (DDLs) et nécessite environ 22 Go de RAM. L’étude se fait de 50 à 1200 Hz par pas de 10 Hz, ce qui prend environ 4 heures (en fonction des ressources de calcul). Notez que la tolérance relative du solveur itératif doit être fixée à 1e-6 pour assurer la convergence du modèle MEF couplé avec les paramètres réduits.

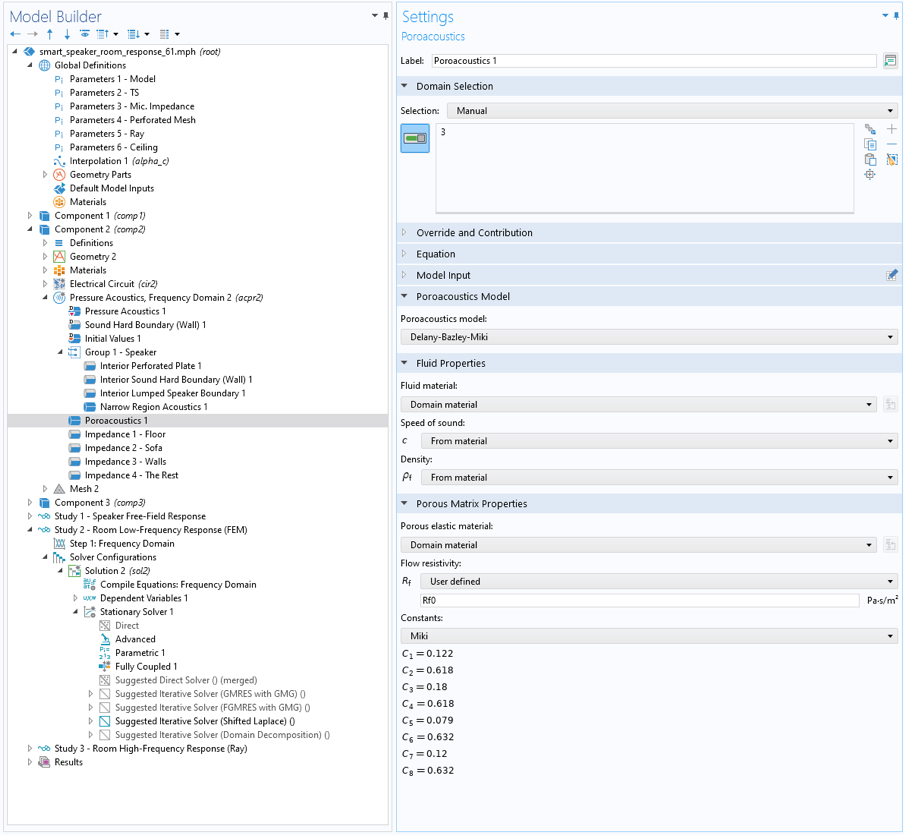
Figure 4. L’interface utilisateur de COMSOL Multiphysics, avec la fonctionnalité Poroacoustique pour modéliser explicitement le plafond suspendu.


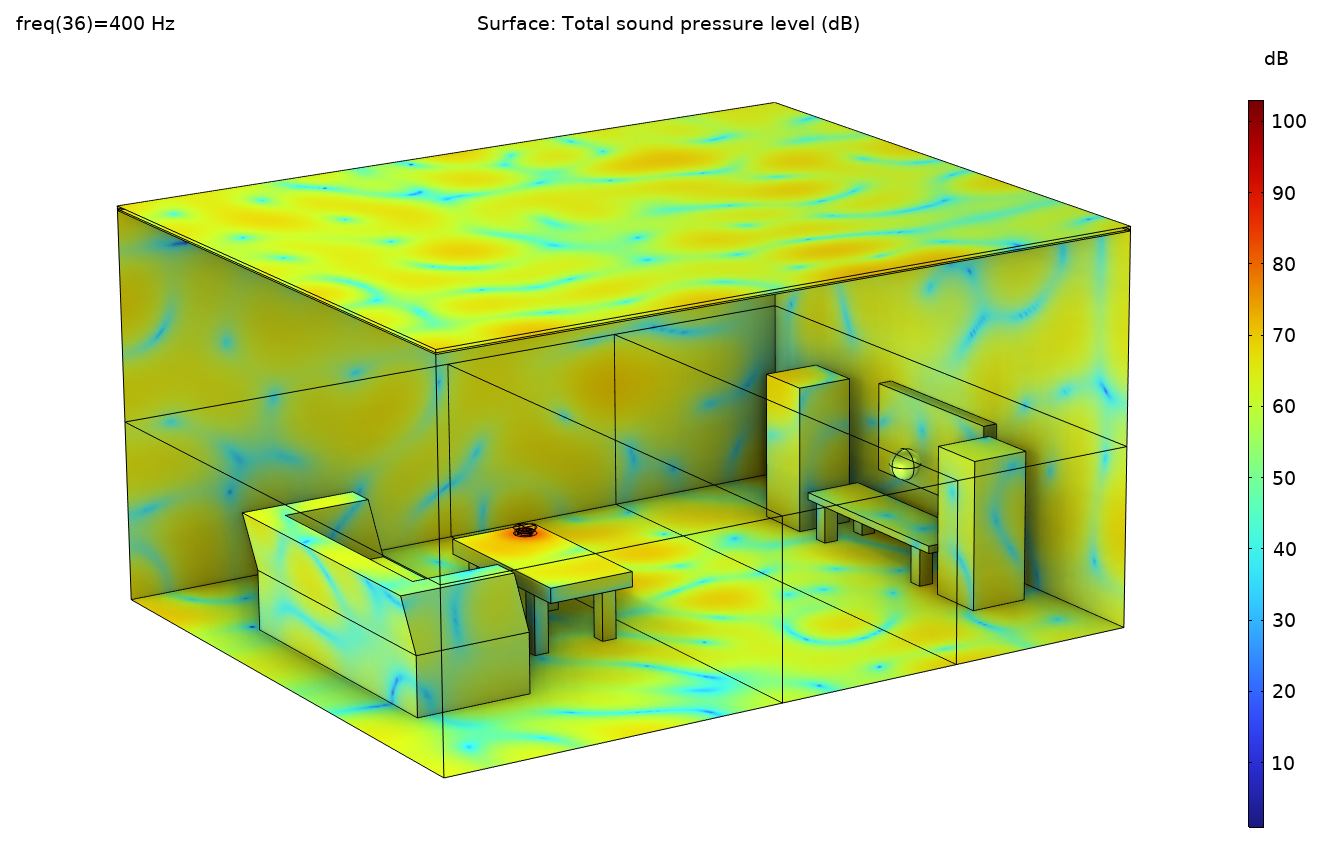
Figure 5. La distribution du niveau de pression acoustique dans la pièce à 400 Hz.

Pour un autre exemple d’utilisation du solveur itératif, consultez le tutoriel Car Cabin Acoustics — Frequency-Domain Analysis.

Hautes fréquences : deux approches

Pour les hautes fréquences, l’interface Rayons acoustiques est utilisée, mais elle est combinée avec les résultats de simulations ondulatoires pour représenter la source du haut-parleur et l’impédance de surface du plafond suspendu, qui dépend de l’angle et de la fréquence. Deux représentations différentes de la source sont utilisées et comparées.

La première méthode sera nommée “Emission à partir d’une source ponctuelle”, et il s’agit en quelque sorte d’un type de source couramment utilisé en lancer de rayons. Les caractéristiques de rayonnement du haut-parleur placé sur un baffle infini (posé sur une table) sont modélisées dans le Composant 1. Il s’agit d’un bon exemple de submodeling, une approche relativement simple à mettre en œuvre dans COMSOL Multiphysics^®. Ces résultats sont directement utilisés pour définir la source ponctuelle de la simulation de rayons acoustiques, par l’intermédiaire de la fonctionnalité Emission à partir du calcul du champ extérieur, définie dans le Composant 3 et résolue dans l’Etude 3. La modélisation du haut-parleur intelligent en termes de physique et de paramètres électroacoustiques est la même entre le submodel de la source et le modèle acoustique complet (basse fréquence) de la pièce.

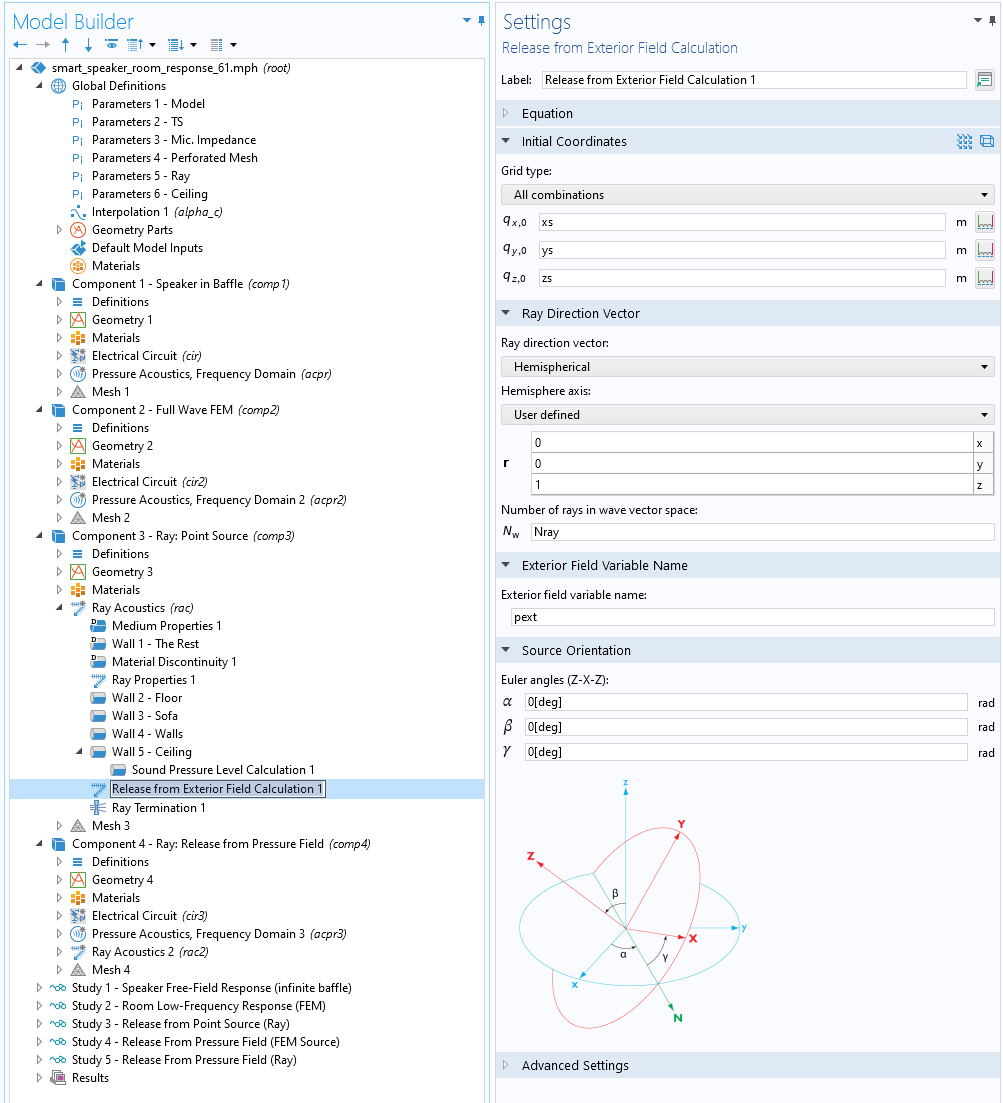
Figure 6. L’interface utilisateur de COMSOL Multiphysics^® montrant la fonctionnalité Emission à partir du calcul du champ extérieur qui couple automatiquement le rayonnement d’un modèle ondulatoire MEF avec un modèle de lancer de rayons.

Dans la seconde méthode de lancer de rayons à haute fréquence, la source n’est pas caractérisée par son rayonnement en champ lointain (comme une source ponctuelle), mais plutôt par ses caractéristiques en champ proche, prenant en compte de manière détaillée la diffusion au niveau des bords de table les plus proches. C’est ce que nous appellerons “l’émission à partir d’un champ de pression”. Dans ce cas, un modèle MEF ondulatoire mis en données avec l’interface Pression acoustique, Domaine fréquentiel est résolu dans une sphère entourant la source (mise en données dans le Composant 4, avec la source résolue dans l’Etude 4). Les rayons sont émis depuis la surface de la sphère dans la direction de l’intensité acoustique (le “vecteur de Poynting acoustique”) et normalisés par l’intensité locale. Cette approche repose sur la fonctionnalité Emission à partir de la frontière de l’interface de rayons acoustiques (mise en données dans le Composant 4, avec la source résolue dans l’Etude 5). Les réglages sont affichés dans la Figure 7 ci-dessous. Notez que la direction d’émission correspond au vecteur d’intensité normalisé \mathbf{I}/|\mathbf{I}|, et la puissance totale de la source (en fonction de la position) est A (\mathbf{I}\cdot\mathbf{n}), où A est la surface totale d’émission et \mathbf{n} est la normale à la surface. Dans les deux cas, les expressions sont entrées avec l’opérateur bndenv(), permettant de projeter la solution MEF sur les rayons.

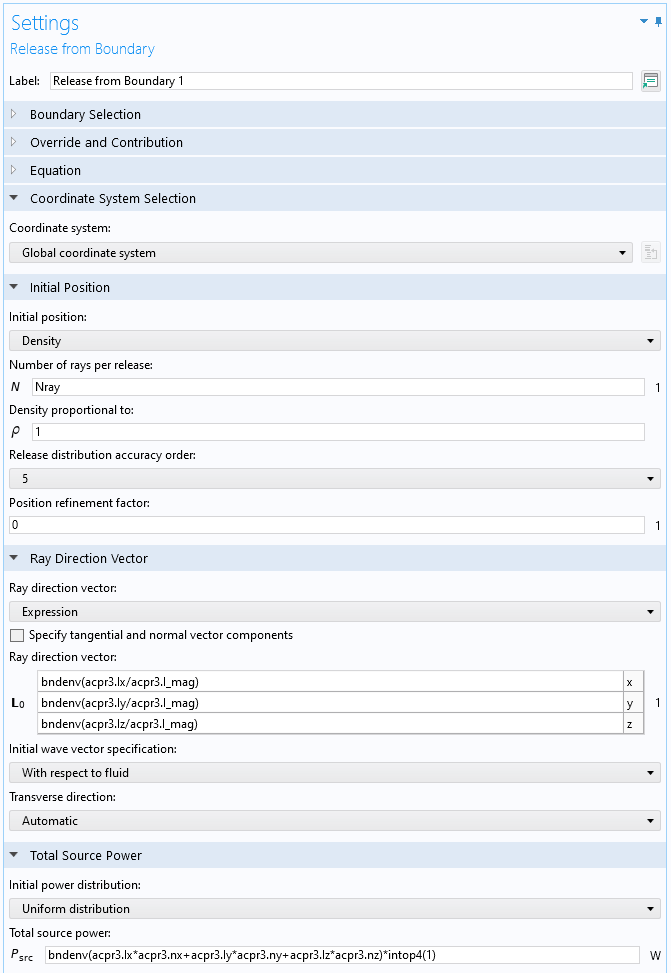
Figure 7. L’interface utilisateur de COMSOL Multiphysics avec les réglages de la fonctionnalité Emission à partir de la frontière .

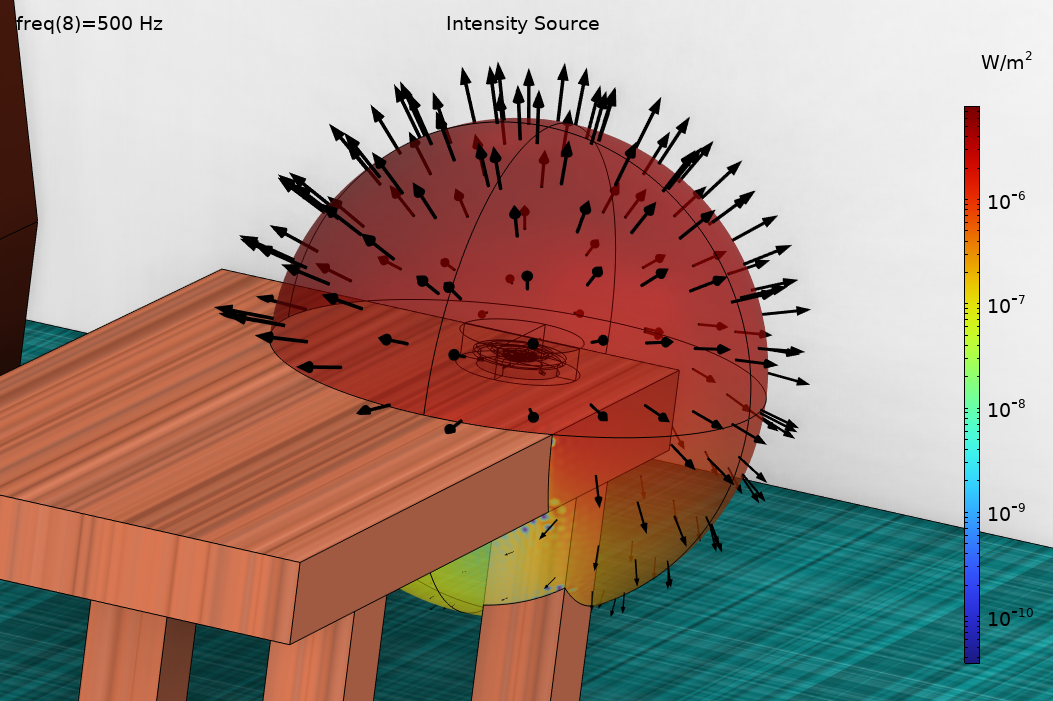
Figure 8. Un exemple montrant les directions et l’intensité des rayons sur la surface d’une sphère d’émission.

La méthode “Emission à partir du champ de pression” combine la méthode ondulatoire (champ proche) avec les hypothèses propres au lancer de rayons. Cela impose également certaines restrictions à l’utilisation de cette formulation pour la mise en place des sources. Par exemple :

1. Lorsque les rayons sont émis à l’aide d’une frontière d’émission, ils sont tous émis en même temps. On peut donc supposer que le son émanant de la source atteint et quitte chaque zone de cette frontière en même temps. Pour que cette hypothèse soit vraie, la frontière d’émission ne peut pas être placée arbitrairement.
2. En raison de la restriction mentionnée au point précédent, il n’est pas aisé de prendre en compte les réflexions internes dans le domaine de la source. Le son peut en effet parcourir des distances différentes en fonction du chemin de réflexion emprunté. La réponse impulsionnelle devrait donc impliquer des événements se produisant à des instants différents à la frontière d’émission.
3. Enfin, le décalage temporel (temps de trajet entre la source et la frontière d’émission) n’est pas inclus dans la réponse impulsionnelle calculée par lancer de rayons. Le logiciel COMSOL^® suppose que les rayons sont émis à l’instant t=0 à la frontière d’émission.

Dans ce modèle, le rayon de la sphère de champ proche est fixé à 0,3 m. Cela permet de capturer la diffraction provenant uniquement des bords de table les plus proches. Cette taille est choisie pour éviter d’alourdir la résolution du problème ondulatoire local, tout en considérant les effets des bords de table les plus proches.

Notez que dans les deux modèles de lancer de rayons, l’absorption du plafond suspendu dépend de l’angle et de la fréquence. Les propriétés sont calculées dans un modèle séparé, illustré ci-dessous.

Propriétés du plafond suspendu

Les propriétés du plafond suspendu sont incluses directement dans l’analyse des basses fréquences en modélisant la couche poreuse (par l’intermédiaire de la fonctionnalité Poroacoustique de l’interface Pression acoustique, Domaine fréquentiel) ainsi que la cavité d’air. Dans la simulation de lancer de rayons (hautes fréquences), les propriétés d’absorption du plafond suspendu sont exprimées sous la forme d’un coefficient d’absorption dépendant de la fréquence et de l’angle d’incidence, \alpha(f,\theta). Les données d’absorption sont extraites d’un submodel du plafond suspendu. Ce modèle est téléchargeable ici. Le modèle est basé sur une approche similaire à celle utilisée dans le tutoriel Porous Absorber. En général, le submodeling est une excellente méthode pour obtenir des conditions limites (et des conditions de source) plus détaillées pour les simulations de lancer de rayons.

L’image ci-dessous montre la surface d’absorption du plafond suspendu du modèle. Le plafond est constitué d’un matériau poreux de 1 cm d’épaisseur avec une résistivité de 20 000 [Pa·s/m²], doublé par une cavité d’air de 2 cm d’épaisseur. Dans le modèle de lancer de rayons, les propriétés dépendantes de la fréquence et de l’angle appellent une fonction d’interpolation prenant comme arguments la fréquence et la variable décrivant l’angle d’incidence rac2.wall5.thetai (avec les numéros de tags : 2 pour le modèle de rayons acoustiques et 5 pour la condition de paroi).

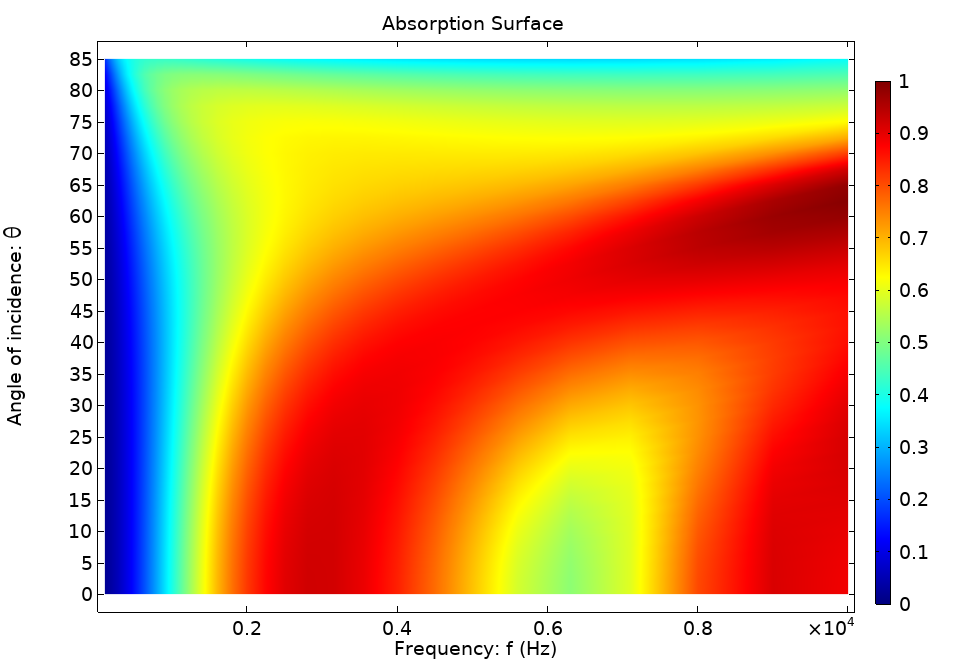
Figure 9. Coefficient de surface d’absorption du plafond suspendu.

Pour des raisons de simplification, le modèle actuel inclut des données d’absorption détaillées uniquement pour le plafond. Le modèle pourrait très bien être enrichi en définissant sur toutes les frontières des données d’absorption dépendant de l’angle et de la fréquence. Concernant la diffusion, des données détaillées peuvent également être calculées à partir de modèles ondulatoires, comme le montre le tutoriel Schroeder Diffuser in 2D.

Considérations des conditions limites

Le modèle présenté ici est utilisable de différentes manières et diverses hypothèses peuvent être formulées en ce qui concerne ses conditions limites. Ces hypothèses diffèrent entre une simulation de pression acoustique et une simulation de rayons acoustiques. Examinons de plus près comment les hypothèses de modélisation changent en fonction du type de simulation.

Tout d’abord, examinons certaines considérations relatives à la pression acoustique :

1. Le déphasage est modélisé ici, c’est pourquoi il est généralement préférable d’utiliser une condition d’impédance dépendant de la fréquence.
2. Typiquement, utiliser uniquement le coefficient d’absorption est imprécis pour les basses fréquences.
3. L’impédance normale d’une surface dépend de l’angle d’incidence. Quelle est donc la valeur à utiliser ? Pour les applications d’acoustique de salles qui n’ont pas d’angle d’incidence clairement défini, l’utilisation d’un angle effectif est souvent bien approprié. Dans le cas, par exemple, de l’option Couche poreuse de la condition Impédance, l’impédance normale est calculée pour un angle d’incidence de 50 degrés avec le réglage Automatique.
4. Pour éviter les hypothèses décrites précédemment, il est préférable, si possible, de modéliser la surface absorbante réelle, comme c’est le cas pour le plafond suspendu de ce modèle.

Dans les simulations de rayons acoustiques, on peut envisager d’utiliser le :

• Coefficient d’absorption d’incidence normale et aléatoire
• Coefficient d’absorption dépendant de l’angle
• Coefficient de diffusion

Le coefficient d’absorption à incidence normale (et aléatoire), le coefficient d’absorption dépendant de l’angle et le coefficient de diffusion peuvent être constants ou dépendre de la fréquence, mais les possibilités de simulation dépendent également des données à votre disposition.

De plus, concernant la simulation de rayons acoustiques, si l’absorption d’un mur varie de manière significative sur une octave, envisagez d’utiliser des bandes plus petites, comme des bandes de 1/3 ou même de 1/6 d’octave.

Résultats

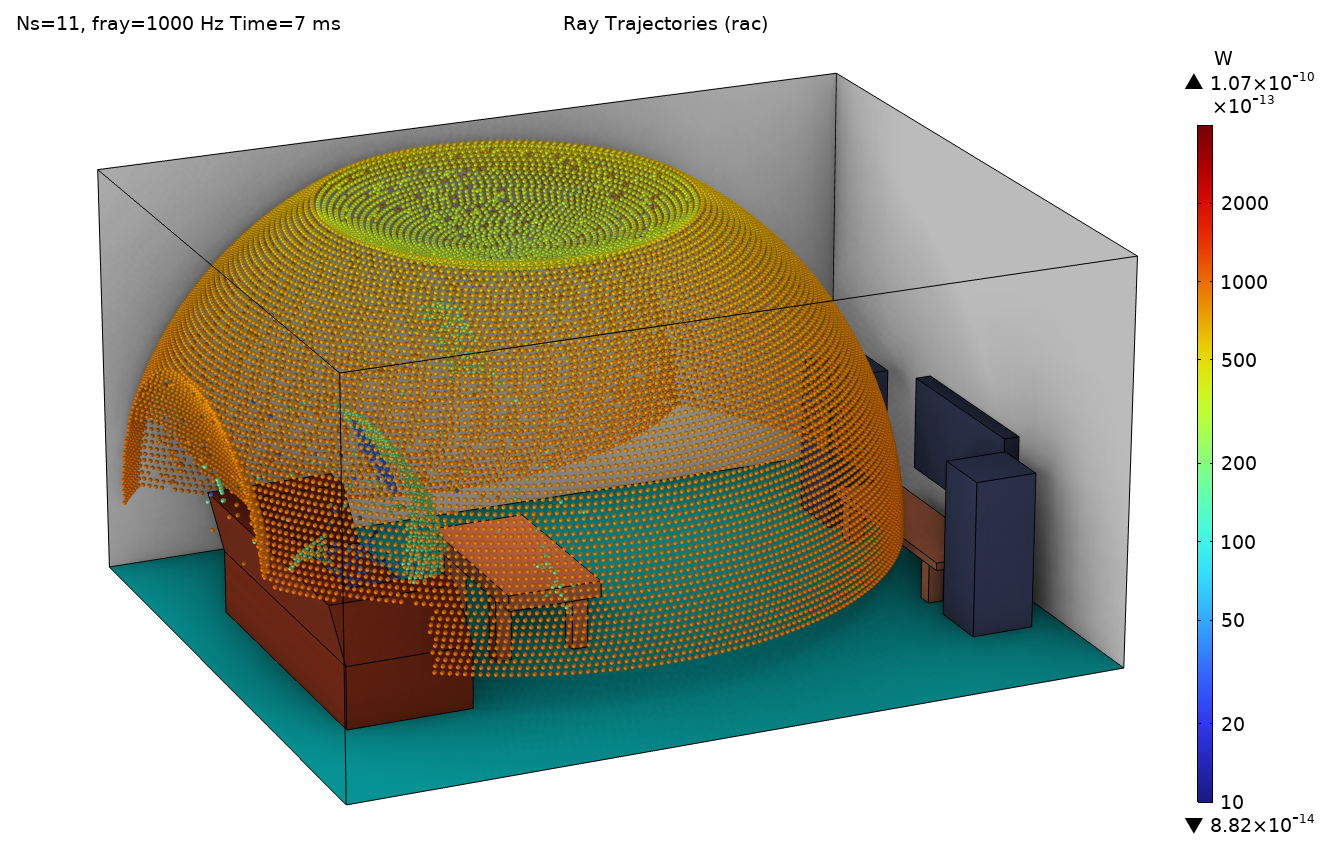
Quelques résultats sélectionnés à partir du modèle exemple sont illustrés sur les figures 10-13. La distribution du champ de pression à 1000 Hz est représentée sur la figure 10, et la forme d’onde de la solution est clairement visible. Sur la figure 11, l’emplacement des rayons de la bande de 1000 Hz est représenté sur le même instant (en corrigeant les différents temps d’émission pour les deux méthodes), en comparant la source ponctuelle avec l’émission à partir du champ de pression. Les images montrent clairement que les deux méthodes donnent des résolutions spatiales (densités de rayons) différentes puisque la source ponctuelle n’émet des rayons que dans la moitié supérieure de l’espace, alors que le champ de pression émet également des rayons vers le bas (en raison de la diffraction autour du bord de la table). Ce comportement devrait être pris en compte pour une comparaison encore plus rigoureuse des méthodes.

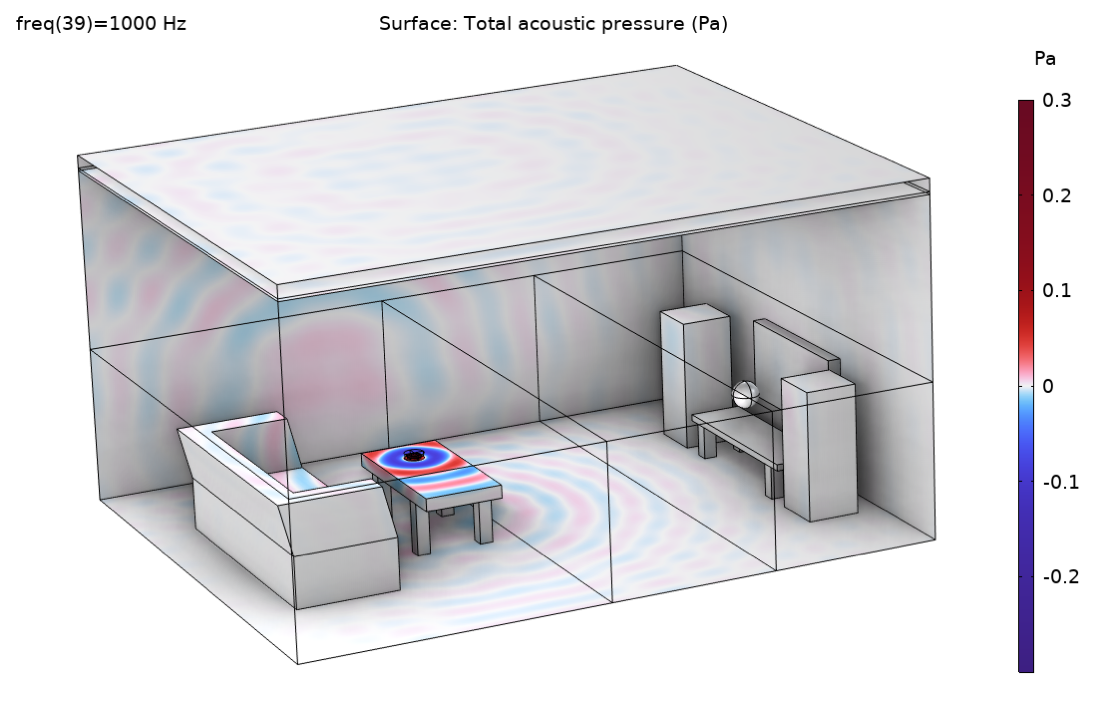
Figure 10. Distribution de la pression à 1000 Hz.

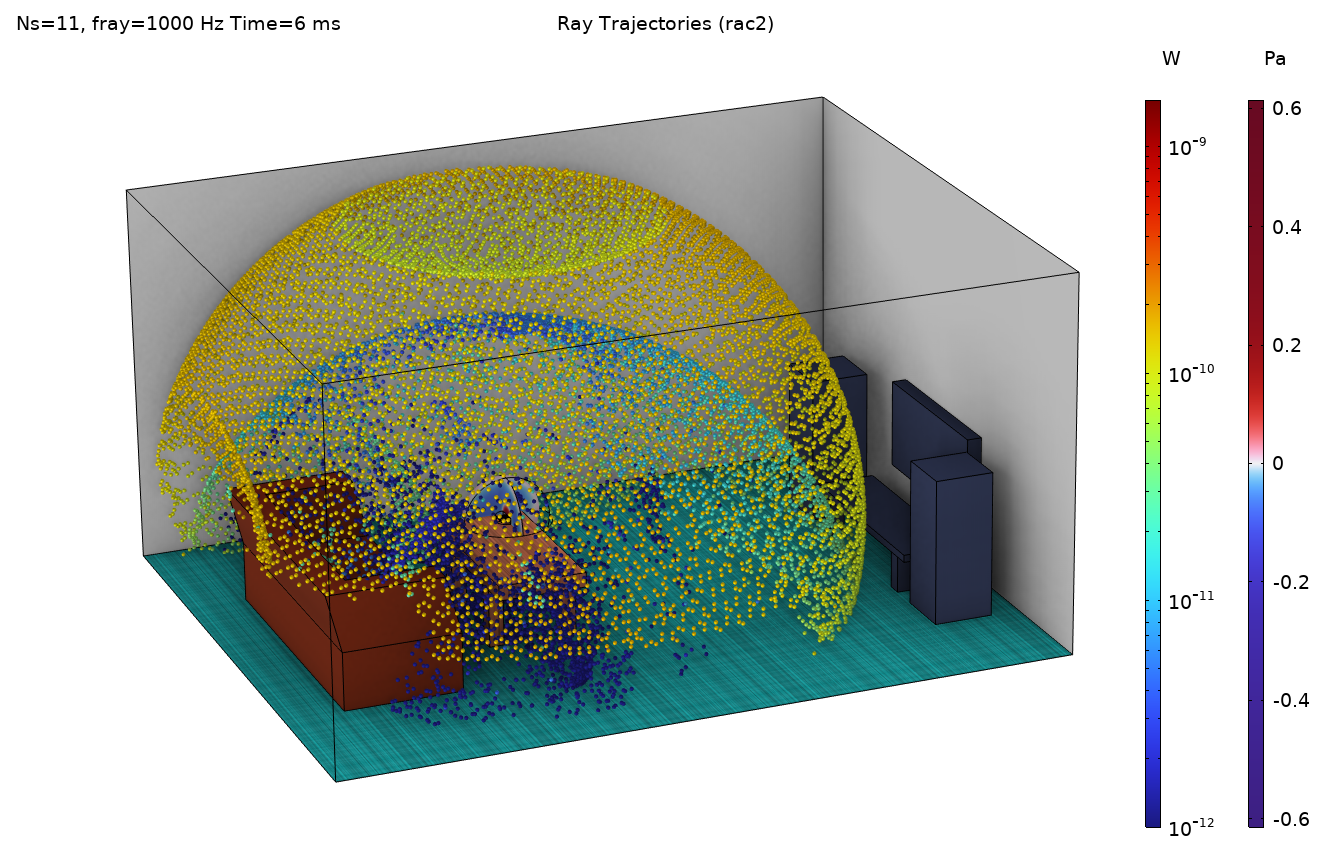
Figure 11. Un graphique de rayons pour la source ponctuelle (à gauche) et pour le champ de pression (à droite). Les deux graphiques montrent la bande de 1-kHz calculée à 6 ms (corrigée de manière approximative par rapport aux définitions différentes du temps 0). Notez les différences d’échelle de la barre de couleurs pour la puissance des rayons. Sur l’image de droite, le champ de pression acoustique proche de la source est également affiché.

Les figures 12 et 13 comparent les deux méthodes. La fonction de transfert entre la source et le récepteur est illustrée sur la figure 12. Elle représente la transformée de Fourier rapide (FFT) de la réponse impulsionnelle (IR) des deux approches de lancer de rayons ainsi que du modèle MEF ondulatoire. Aucun lissage n’est appliqué sur les résultats de la MEF, mais un filtre de 1/3 d’octave est appliqué sur les résultats du lancer de rayons. Le graphique montre le même comportement global. Il met également en évidence un comportement modal important de la pièce, même au-dessus de la fréquence de Schroeder attendue (ligne verticale). Il semble y avoir une différence non négligeable entre les deux résultats de rayons acoustiques (courbes bleues et rouges). Cela pourrait s’expliquer par le fait que l’énergie est diffusée différemment par les deux types de sources. Enfin, certaines caractéristiques temporelles des deux résultats de lancer de rayons sont comparées dans la figure 13. Le temps de décroissance (EDT) et le temps de réverbération (T20) sont comparés. Le graphique met en évidence une différence significative entre les deux, ce qui indique que la distribution temporelle d’énergie parvenant au récepteur est différente pour les deux modèles.

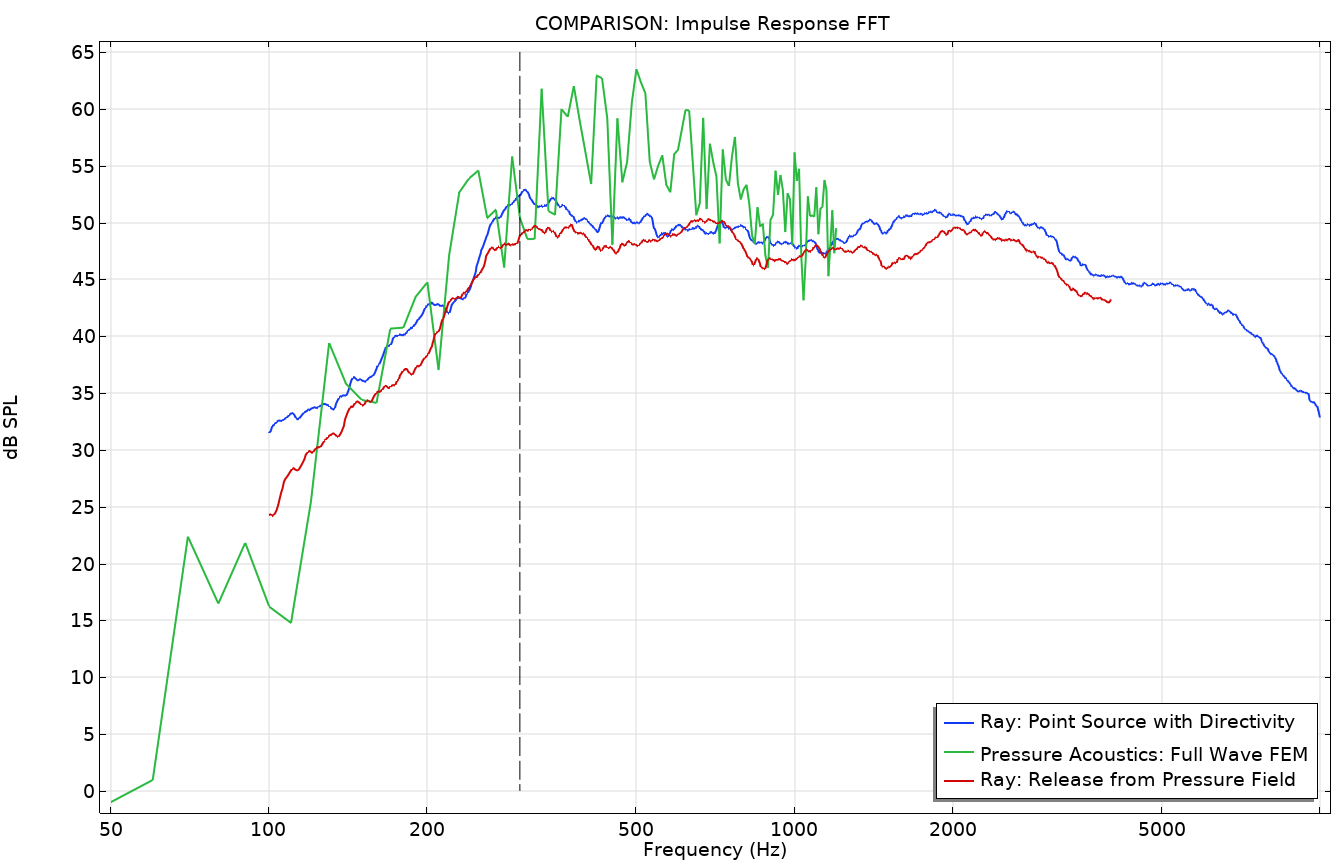
Figure 12. Réponses impulsionnelles FFT en acoustique ondulatoire et en rayons acoustiques.

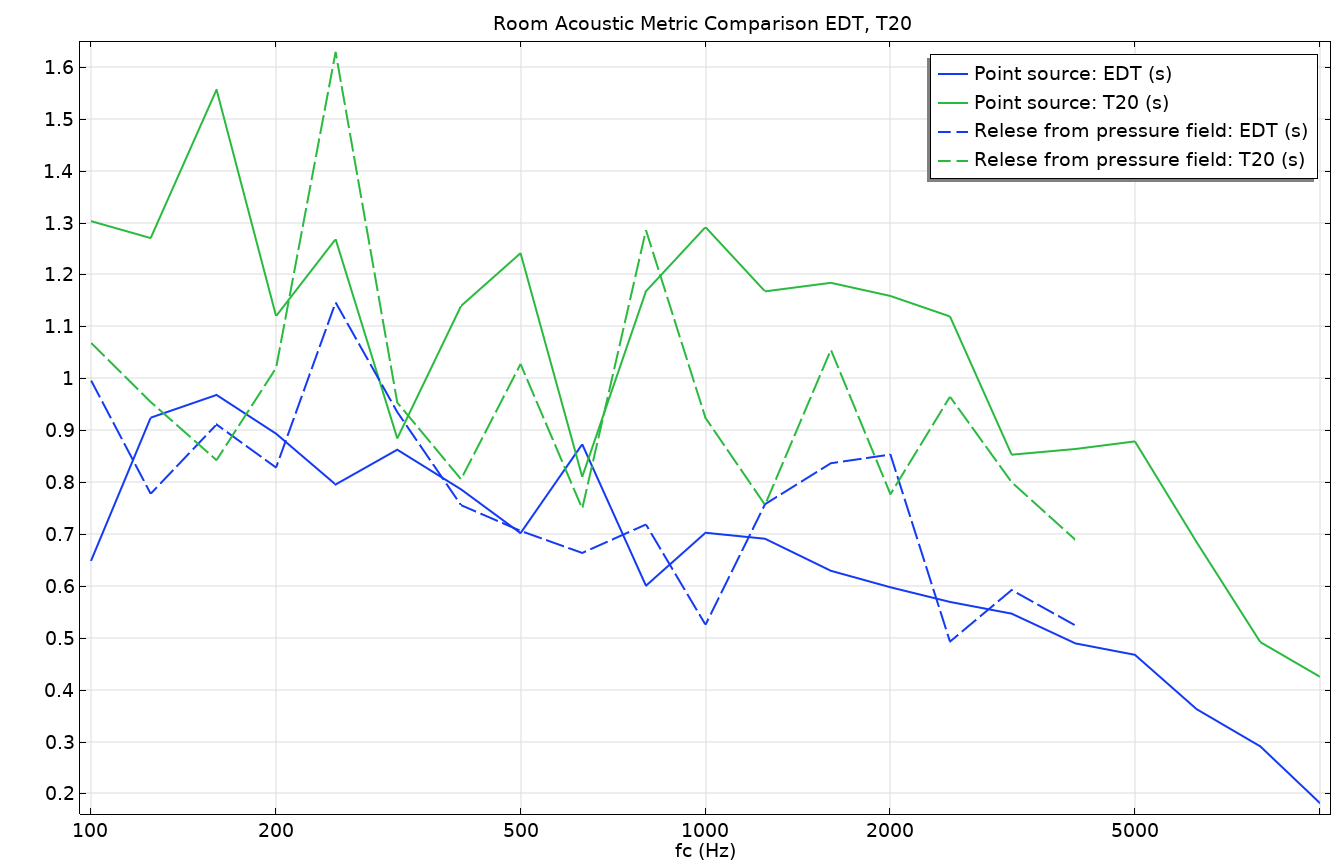
Figure 13. Indicateurs d’acoustique des salles comparant le temps de réverbération pour l’EDT et la T20.

Certains résultats exposés ici peuvent être affinés pour étendre l’analyse de ce modèle. Par exemple, vous pouvez utiliser un plus grand nombre de rayons, comparer plusieurs positions de récepteur, utiliser une résolution de fréquence plus fine pour le modèle MEF ou utiliser une bande de 1/6 d’octave pour le modèle de lancer de rayons. Ces différentes possibilités sont toutes réalisables à partir du modèle présenté. Vous pouvez par exemple changer le nombre de rayons en modifiant le paramètre Nrays ou changer la position du récepteur en modifiant les paramètres xr, yr, et zr.

Prochaines étapes

Explorez plus en détails le modèle de cet article de blog en cliquant sur le bouton ci-dessous, qui vous mènera à la Bibliothèque d’Applications.

Ressources complémentaires

• Apprenez en plus sur la modélisation d’acoustique des salles dans le blog COMSOL :
  • Modeling Room Acoustics Using a Hybrid Approach
  • Validating an Acoustic Ray-Tracing Simulation of a Chamber Music Hall
• Consultez ce tutoriel en lien avec le sujet :
  • Schroeder Diffuser in 2D