
A la suite du précédent blog sur l’amortissement en dynamique des structures, nous examinons en détail la réponse harmonique des systèmes mécaniques amortis. Nous montrons également différentes façons de mettre en place une analyse de réponse en fréquence dans le logiciel COMSOL Multiphysics®, ainsi que la manière d’interpréter les résultats.
Qu’est-ce que la réponse en fréquence ?
D’une manière générale, la réponse en fréquence d’un système indique comment une propriété de ce système répond à une sollicitation en fonction de la fréquence d’excitation. Lorsque l’on parle de réponse en fréquence dans COMSOL Multiphysics®, il s’agit généralement de la réponse linéaire (ou linéarisée) à une excitation harmonique. Pour obtenir une courbe de réponse en fréquence, il est nécessaire d’effectuer un balayage en fréquence, c’est-à-dire de résoudre le problème pour un certain nombre de fréquences différentes. Une courbe de réponse en fréquence présentera, en général, un certain nombre de pics distincts se situant aux fréquences propres du système.
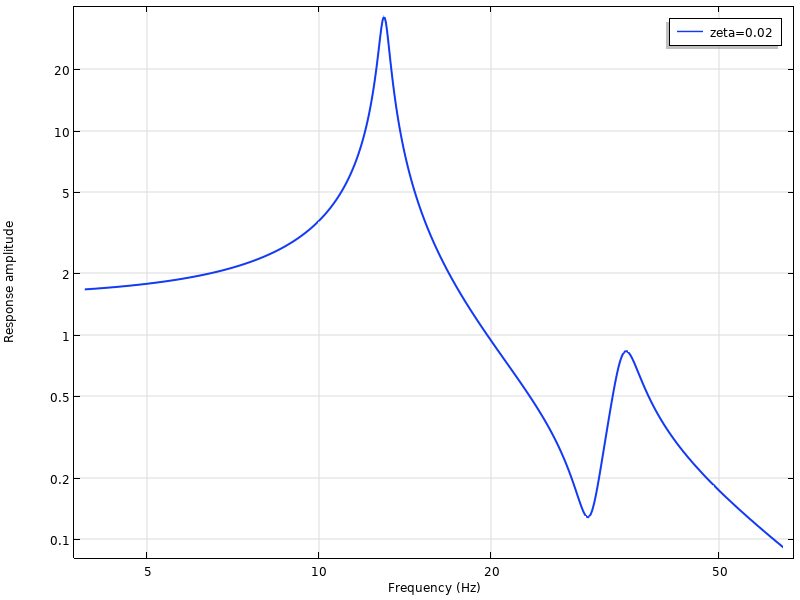
Une courbe typique de réponse en fréquence. Il y a deux fréquences propres à 13 Hz et 31 Hz dans la plage balayée.
Le système à un seul degré de liberté, revisité
Différents aspects de dynamique pour un système à un seul degré de liberté avec amortissement visqueux ont été abordés dans le précédent blog. Parmi ces aspects, on sait que la fréquence propre amortie peut être déterminée par
\omega_d = \omega_0\sqrt{1-\zeta^2} \approx \omega_0 \left ( 1 – \frac{\zeta^2}{2} \right )
Il s’agit de la fréquence à laquelle le système vibrera (avec une amplitude décroissante) s’il est relâché à partir d’un état déformé, en l’absence de toute autre sollicitation extérieure.
Une question pertinente se pose alors : “Quelle est la fréquence d’excitation qui donnera l’amplitude maximale de réponse?” On pourrait s’attendre à ce que ce soit précisément la fréquence propre amortie, mais comme nous le montrerons plus loin, ce n’est pas le cas.
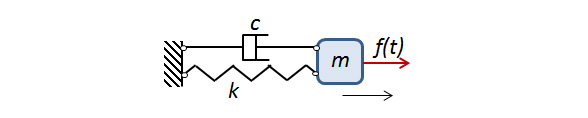
Un système à un seul degré de liberté.
Comme il s’agit d’un mouvement harmonique, il est judicieux d’utiliser une notation complexe, en factorisant par le multiplicateur exponentiel commun e^{i \omega t}. L’équation du mouvement est alors
\left (-\omega^2m +ic\omega +k \right) u = f
La phase du chargement f peut être prise comme référence afin que f soit de valeur réelle. Une forme normalisée peut être obtenue en divisant par la rigidité k:
\left (1-\left (\frac{\omega}{\omega_0} \right) ^2 +2i\zeta \left (\frac{\omega}{\omega_0} \right) \right) u = \frac{f}{k}
Le terme de droite est désormais précisément le déplacement statique. Ainsi, le rapport entre les solutions dynamique et statique est égal à
\displaystyle H(\omega) = \left (1-\left (\frac{\omega}{\omega_0} \right) ^2 +2i\zeta \left (\frac{\omega}{\omega_0} \right) \right)^{-1} =\frac{1}{1-\beta ^2 +2i\zeta \beta}
La fonction H est parfois appelée la fonction de transfert.
Ici, β est utilisé pour désigner le rapport entre la fréquence d’excitation et la fréquence propre non amortie. L’amplitude de la fonction de transfert est
\displaystyle \left | \frac{1}{1-\beta ^2 +2i\zeta \beta} \right | = \frac{1}{\sqrt {(1-\beta ^2)^2 +4\zeta^2 \beta^2}}
La fonction est représentée dans le graphique ci-dessous.
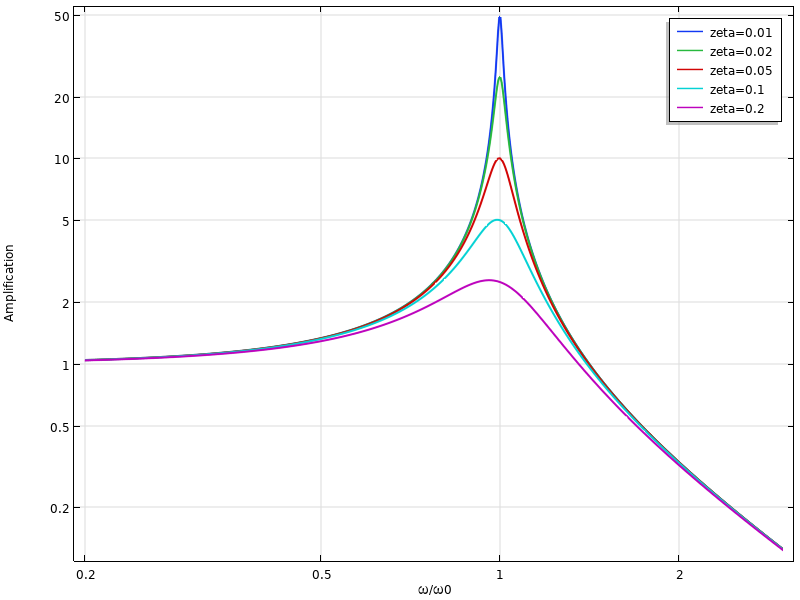
A partir de calculs standards, la fréquence donnant l’amplitude maximale peut être déterminée en trouvant le minimum du dénominateur (élevé au carré) {(1-\beta ^2)^2 +4\zeta^2 \beta^2}. Le résultat est
\beta = \sqrt{1-2 \zeta^2}
Ainsi, la fréquence d’excitation donnant la réponse maximale est
\omega_{\mathrm {max}} = \omega_0\sqrt{1-2\zeta^2} \approx \omega_0 \left ( 1 – \zeta^2 \right )
qui est plus basse que la fréquence propre amortie. En réalité, le décalage en fréquence est deux fois plus important.
Le fait que la fréquence d’excitation provoquant l’amplitude maximale ne coïncide pas avec la fréquence de vibrations libres peut sembler paradoxal. Cela peut être attribué au déphasage entre la force et le déplacement causé par l’amortissement. Sans amortissement, la charge et le déplacement sont parfaitement en phase pour les fréquences inférieures à la fréquence propre et ils deviennent déphasés de 180° pour les fréquences supérieures à la fréquence propre. Avec l’amortissement, la transition du déphasage est plus progressive, comme le montre le graphique ci-dessous. Quel que soit le niveau d’amortissement, le déphasage à la fréquence propre non amortie est toujours de 90°.
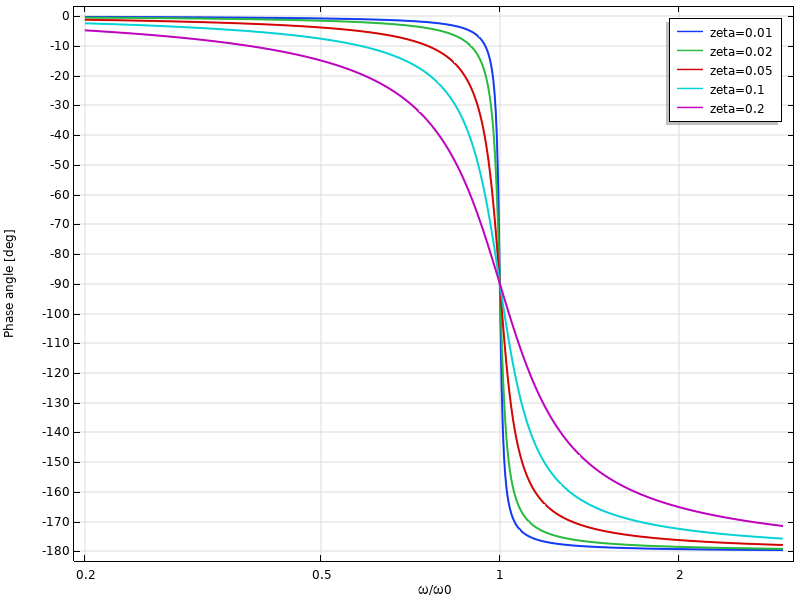
Déphasage du déplacement en fonction de la fréquence.
Le fait que la force et le déplacement soient légèrement déphasés en cas d’amortissement affecte la capacité de la force à fournir de l’énergie au système.
Facteur de perte
Répétons l’analyse pour un système à un seul degré de liberté avec un facteur de perte. Dans ce cas, l’équation du mouvement est
\left (-\omega^2m +k(1+i\eta ) \right) u = f
et la fréquence propre amortie peut être exprimée comme étant
\displaystyle \omega_d = \omega_0 \sqrt {\left( \frac{1}{2} \left( 1 + \sqrt{1+\eta^2} \right ) \right ) } \approx \omega_0 \left (1 + \frac{\eta^2}{8} \right )
Il peut sembler surprenant qu’ajouter de l’amortissement sur ce cas fasse augmenter la fréquence propre, plutôt que de la diminuer. L’explication est que cette formulation du facteur de perte augmente également la rigidité. La valeur absolue de la rigidité à valeur complexe est
|\tilde k| = k \sqrt {1 + \eta^2} \approx k \left ( 1+ \frac{\eta^2}{2} \right )
Avec ce facteur de perte, la fonction de transfert est
\displaystyle \frac{1}{1-\beta ^2 +i\eta }
et son amplitude est
\displaystyle \left | \frac{1}{1-\beta ^2 +i\eta} \right | = \frac{1}{\sqrt {(1-\beta ^2)^2 +\eta^2}}
On constate immédiatement que l’amplitude maximale se produit à β = 1, c’est-à-dire à la fréquence propre non amortie. Une fois encore, l’amplitude maximale se produit à une fréquence inférieure à la fréquence propre amortie.
La définition alternative du facteur de perte mentionnée dans le blog précédent possède comme propriété que la valeur absolue de la rigidité complexe est indépendante du niveau d’amortissement. Cette propriété s’obtient en utilisant une définition qui normalise la rigidité complexe de manière à obtenir une rotation pure dans le plan complexe,
\tilde k = \displaystyle \frac{k(1+i \eta)}{\sqrt{1+ \eta^2}}
Une telle formulation conduit à une fréquence propre qui diminue avec l’amortissement :
\displaystyle \omega_d = \omega_0 \sqrt { \frac {\frac{1}{2} \left( 1 + \sqrt{1+\eta^2} \right )}{1+ \eta^2} } \approx \omega_0 \left (1 – \frac{3\eta^2}{8} \right )
Une étude qui n’est pas abordée ici montre une baisse correspondante de la fréquence d’excitation donnant l’amplitude maximale, de manière à ce qu’elle soit toujours inférieure à la fréquence propre amortie.
Le déphasage entre l’excitation et la réponse lors de l’utilisation du facteur de perte est particulièrement intéressant : même à des fréquences d’excitation très basses, il y a toujours un déphasage. Sa valeur asymptotique est arctan(η).
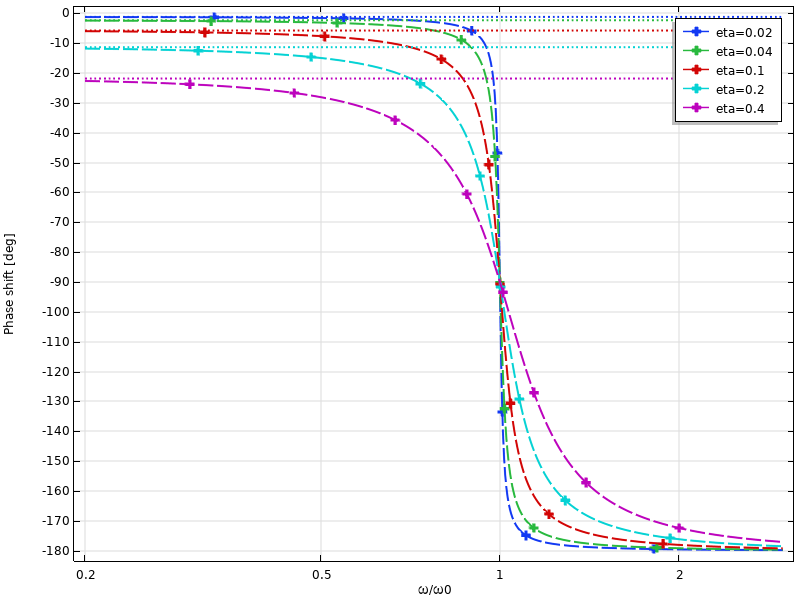
Déphasage du déplacement en fonction de la fréquence lors de l’utilisation d’un facteur de perte. Les asymptotes à basse fréquence sont indiquées par les lignes pointillées.
Note sur le frottement
Lorsque le frottement entre deux surfaces constitue le mécanisme d’amortissement, la réponse à une excitation harmonique n’est plus harmonique en raison de la non-linéarité du système. Il peut toujours y avoir une réponse périodique, mais non harmonique. De tels problèmes ne peuvent pas être résolus par les méthodes de domaine fréquentiel, celles-ci reposant sur une hypothèse de relation linéaire entre sollicitation et réponse.
Modéliser une réponse en fréquence dans COMSOL Multiphysics®
Mise en place de l’étude
Après avoir ajouté une interface physique de mécanique du solide dans le Constructeur de modèles, un certain nombre de types d’études vous sont proposés, dont quatre peuvent être utilisés pour calculer une réponse en fréquence :
- Domaine fréquentiel
- Domaine fréquentiel, précontraint
- Fréquentiel sur base modale
- Domaine fréquentiel, précontraint, modal

Types d’études disponibles pour une interface Mécanique du solide.
Deux de ces études utilisent une approche de résolution directe et les deux autres utilisent une approche de superposition modale. Pour les analyses de types précontraintes, le changement de rigidité à partir d’un chargement préliminaire stationnaire est pris en compte. La superposition modale est très bien adaptée à une analyse en domaine fréquentiel, car il est aisé de sélectionner les modes propres appropriés correspondant aux fréquences données.
Dans les deux cas, vous effectuez un balayage en fréquences en fournissant une liste de fréquences dans les réglages de l’étude pour lesquelles la réponse doit être calculée. Souvent, vous souhaitez répartir ces fréquences autour des fréquences propres de la structure.
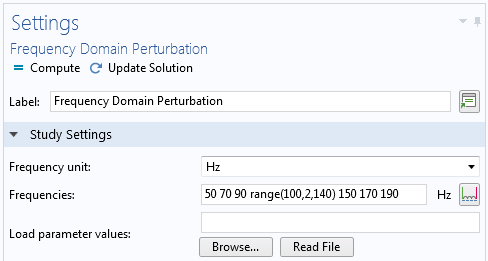
Saisie des fréquences pour un balayage en fréquences.
Notez que sans amortissement, la réponse exacte à une fréquence propre tend vers l’infini. Cela signifie qu’il n’est pas possible de résoudre un problème de réponse en fréquence sans amortissement à une fréquence égale ou proche d’une fréquence propre. La formulation numérique donnera une matrice singulière, ou du moins, mal conditionnée.
Perturbation ou non?
Il y a un réglage très important dans le noeud Stationnaire de la séquence solveur d’une étude de domaine fréquentiel: Linéarité.
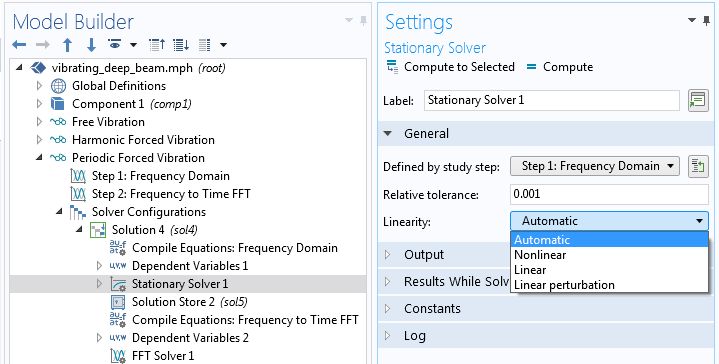
Sélection du réglage Linéarité.
En principe, toute analyse en domaine fréquentiel peut être considérée comme une petite perturbation, de sorte qu’utiliser la Perturbation linéaire n’est jamais mauvaise. Le cas le plus courant, cependant, est celui où les vibrations sont centrées autour de zéro. Dans ce cas, il n’est pas réellement important de savoir si le problème est considéré comme Linéaire ou Perturbation linéaire. Toutefois, ce réglage altère systématiquement l’interprétation du chargement de façon fondamentale. Un chargement peut être identifié dans l’interface comme Perturbation harmonique. Un tel chargement est pris en compte seulement si le réglage Linéarité est défini sur Perturbation linéaire. Tous les chargements qui ne sont pas identifiés comme Perturbation harmonique sont ignorés dans une telle étude. Inversement, si Linéarité n’est pas défini sur Perturbation linéaire, alors tous les chargement identifiés comme Perturbation harmonique sont ignorés, et les autres chargements sont considérés comme harmoniques.

Un chargement sur arête, identifié comme Perturbation harmonique.
Le but de ce réglage est de pouvoir faire la distinction entre les chargements provoquant un état de précontrainte possible et l’excitation harmonique agissant en plus.
Lorsque vous ajoutez une étude standard Domaine fréquentiel, l’étude par défaut n’est pas définie en tant que perturbation. Par conséquent, l’option Perturbation harmonique dans ce cas, ne doit pas être utilisée pour les chargements, à moins que vous ne changiez le réglage Linéarité. Lorsque vous ajoutez une étude Domaine fréquentiel, précontraint, l’étape de l’étude de réponse en fréquence est configurée pour une analyse de perturbation. Si l’étude est de type superposition modale, alors l’étude est toujours de type perturbation linéaire.
Interprétation des résultats
Les résultats d’une analyse en domaine fréquentiel sont des valeurs complexes et la variation harmonique est implicite. L’argument du nombre complexe décrit le déphasage par rapport à la phase de référence (qui peut être choisie arbitrairement, mais qui est souvent la phase du chargement principal). Il fournit également des informations sur le déphasage entre différents points de la structure. Il convient de noter que, puisque les composantes du déplacement au sein d’un même élément fini peuvent avoir des phases différentes, il est tout à fait possible que les composantes du tenseur des contraintes ne soient pas en phase les unes avec les autres. Cela peut être important, par exemple, dans une analyse de fatigue.
Dans de nombreux cas, comme un graphique de champs en couleurs, il est seulement possible d’afficher un nombre réel. La convention pour représenter les résultats est la suivante : si vous renseignez une variable à valeur complexe v dans le cas où une valeur réelle est attendue, la partie réelle est utilisée.
\displaystyle v = \Re(\tilde v e^{i \phi})
La phase Φ est une propriété du jeu de données que vous pouvez modifier.
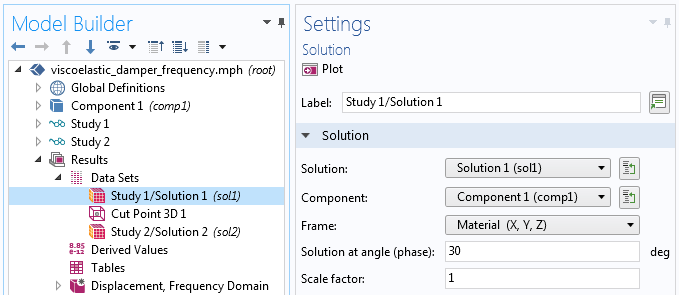
Ajustement de la phase dans le jeu de données.
Dans la plupart des analyses fréquence-réponse, on s’intéresse à l’amplitude d’une quantité résultat, v, en fonction de la fréquence. Cela signifie qu’on devrait étudier abs(v) plutôt que v lui-même. La différence entre les deux est illustrée dans le graphique ci-dessous.
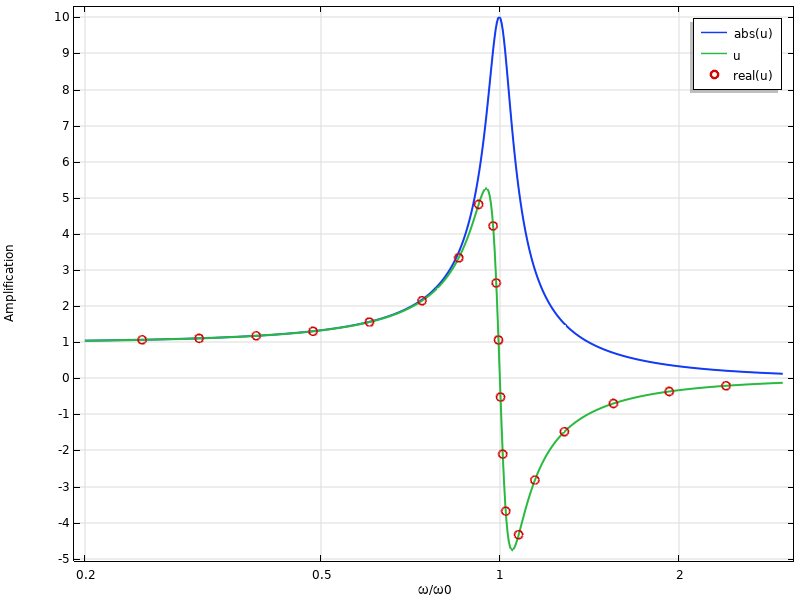
Exemple de graphique de réponse en fréquence. Notez que la courbe de “u” est identique à celle de “real(u)”.
Afin de visualiser plus en détail ce qui se passe, nous pouvons ajouter au graphique la partie imaginaire et l’argument de la quantité résultat :
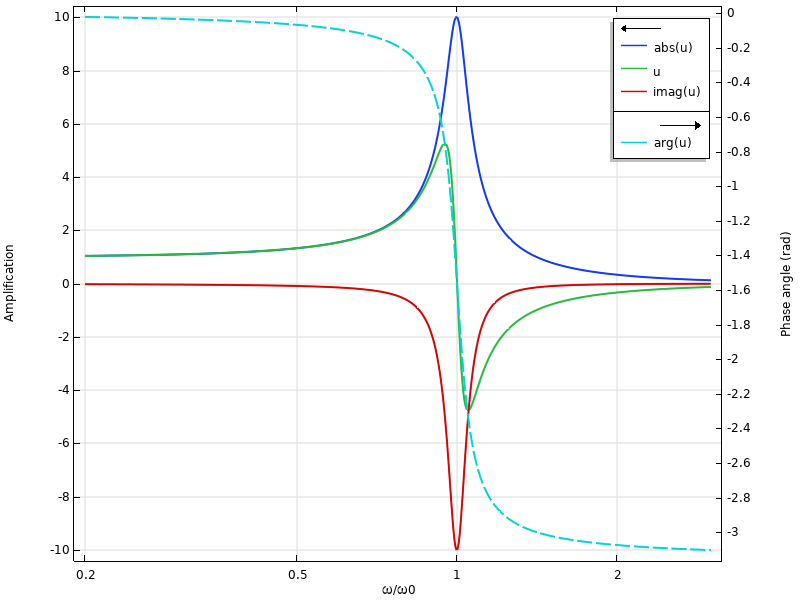
Réponse en fréquence, incluant le déphasage.
Pour les basses fréquences, la partie réelle est proche de la valeur absolue. Au voisinage de la fréquence propre, la partie imaginaire est dominante. Cela signifie que la réponse est pratiquement déphasée par rapport à l’excitation.
Voyons maintenant ce qui se passe si nous modifions la phase du jeu de données à 45°.
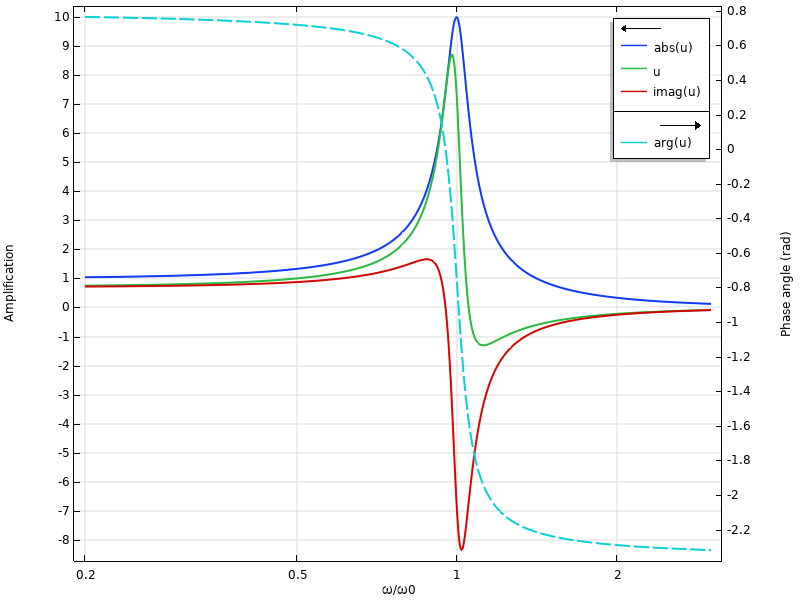
Réponse en fréquence lorsque la phase du jeu de données est de 45°.
Comme prévu, la courbe d’amplitude ne change pas. Cependant, les valeurs respectives de la partie réelle et de la partie imaginaire sont modifiées. La courbe de la phase est décalée de π/4 vers le haut. En fait, il s’agit exactement du même graphique que nous obtiendrions si un déphasage de 45° était ajouté au chargement.
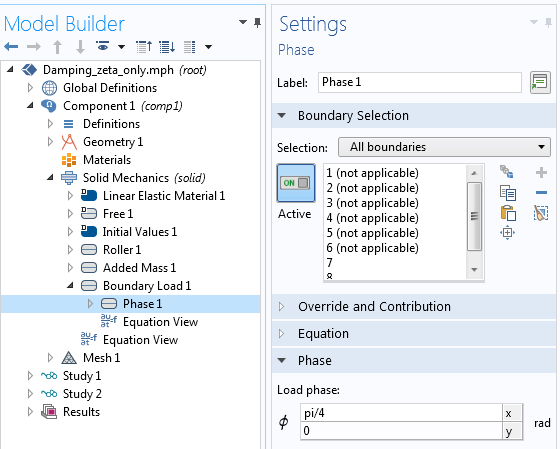
Ajout d’un déphasage sur un chargement.
Au lieu d’utiliser la condition de phase, vous pouvez de manière équivalente entrer la charge directement en utilisant la notation complexe :
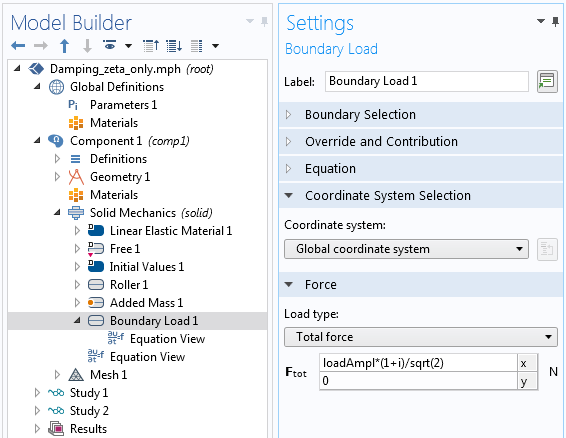
Notation complexe du même chargement que celui présenté précédemment.
La possibilité de définir la phase est importante lorsque tous les chargements sont déphasés les uns par rapport aux autres. Une masse déséquilibrée en rotation peut, par exemple, être décrite de manière pratique en donnant au chargement dans la direction y un déphasage de 90° par rapport au chargement dans la direction x.
Résultats d’une étude de perturbation
Si l’étude est de type perturbation, il y aura en fait deux jeux de données : la solution précontrainte et la solution de la perturbation. Dans ce cas, vous aurez accès à une option supplémentaire dans les différentes fonctionnalités d’exploitation de résultats : Expression évaluée pour.
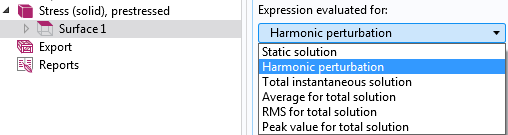
Sélection du type d’évaluation pour une analyse de perturbation.
Ici, vous pouvez choisir d’étudier la solution de la perturbation, la solution précontrainte ou des combinaisons de celles-ci. Pour la solution de la perturbation, vous disposez d’une option supplémentaire: la case Calculer le différentiel.

Activation de Calculer le différentiel.
Cette option affecte le traitement des expressions non linéaires. Si l’option Calculer le différentiel n’est pas activée, alors toute quantité non linéaire est prise à sa valeur nominale. Par exemple, l’expression u^2 prendra simplement le carré de la variable u de la solution de la perturbation. Étant donné que u est, en général, une valeur complexe, cette opération n’a généralement pas de sens.
Lorsque Calculer le différentiel est activé, alors la quantité non linéaire sera linéarisée autour de l’état précontraint. L’expression u^2 sera évaluée par 2*u0*u, où u0 est la valeur au point de linéarisation.
Conversion des résultats de réponse en fréquence dans le domaine temporel
Dans certaines situations, vous souhaitez visualiser la réponse harmonique d’une analyse de domaine fréquentiel dans le domaine temporel. C’est notamment le cas lorsque vous avez de multiples fréquences d’excitation.
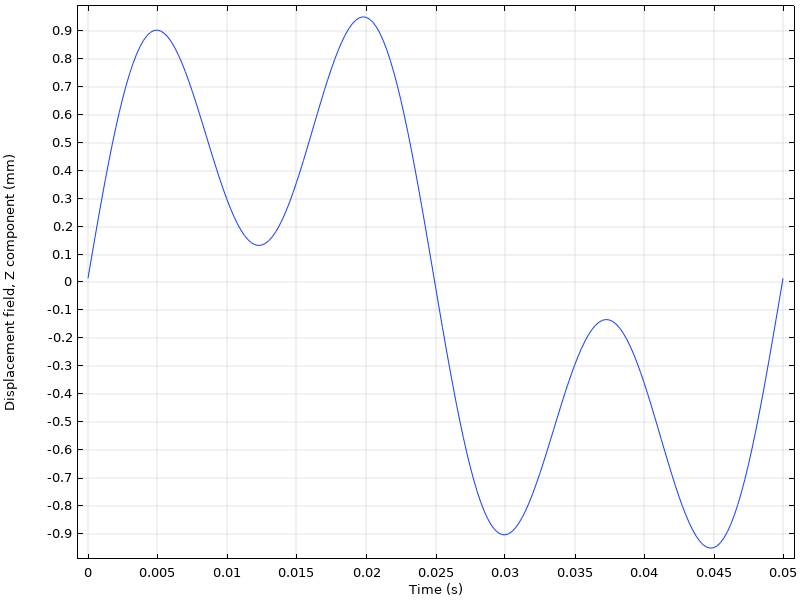
Réponse à l’excitation de deux chargements ayant des fréquences différentes.
Vous pouvez transformer les résultats de la réponse en fréquence dans le domaine temporel à l’aide de l’étape d’étude FFT fréquentiel vers temporel.

Séquence d’étude pour transformer les résultats du domaine fréquentiel vers le domaine temporel.
Cette technique est utilisée dans les tutoriels suivants :
Conclusion
L’analyse en domaine fréquentiel est un outil puissant pour étudier les systèmes linéaires soumis à une excitation harmonique. En effet, en effectuant une première transformée de Fourier du chargement, tout type d’excitation périodique peut être étudié à l’aide d’une analyse de réponse en fréquence.
De nombreux autres exemples d’analyses de réponse en fréquence sont disponibles dans la Bibliothèque d’Applications :




Commentaires (0)