
Il y a toujours eu un débat parmi les ingénieurs travaillant sur les écoulements de fluides sur la pertinence des méthodes des éléments finis pour la CFD. Certains ingénieurs ont un avis tranché sur la supériorité des méthodes des volumes finis comparé aux méthodes des éléments finis. Cette opinion est-elle étayée scientifiquement? Non, pas en général. Différentes méthodes peuvent convenir à différents problèmes. Voyons pourquoi.
Science, technologie, et tradition
Les méthodes des éléments finis sont largement utilisées par la communauté de l’analyse numérique pour l’étude de méthodes numériques pour des écoulements de fluides. De nombreux travaux concernant la CFD et les méthodes des éléments finis sont décrits dans les publications scientifiques ainsi que des travaux plus récents à propos des méthodes de Galerkin discontinues (DG), qui sont des méthodes d’éléments finis avec des fonctions de base discontinues.
Les logiciels commerciaux de CFD sont traditionnellement basés sur des méthodes de volumes finis. Cela est dû au fait que pratiquement tous les grands logiciels commerciaux de CFD ont les mêmes prédécesseurs. Beaucoup de travail et de technologie ont été investis dans ces méthodes dans l’industrie. Des méthodes différentes ont été implémentées afin de calculer et d’intégrer de façon efficace et précise les flux sur des maillages structurés (par exemple, des hexaèdres; i.e., des briques) et non structurés (par exemple, des tétraèdres).
Cela dit, il n’y a aucun argument théorique ou pratique permettant d’étayer l’hypothèse selon laquelle les méthodes des volumes finis seraient supérieures aux méthodes des éléments finis pour des écoulements. Tout d’abord, il existe de nombreuses méthodes de volumes finis et d’éléments finis, et certaines se recoupent. Ensuite, la façon dont une méthode est mise en oeuvre a un impact très important sur l’utilisation pratique d’un logiciel. Nous pouvons dire que le logiciel X semble mieux fonctionner que le logiciel Y pour un certain type de problèmes. Ce n’est cependant pas parce que l’un utilise la FEM et l’autre la FVM. Expliquons cela ci-dessous.
Eléments finis contre volumes finis: qui est meilleur?
Modèles mathématiques et modèles numériques
Commençons avec un modèle mathématique générique:
(1)
(2)
u = f{\text{ condition initiale}} \hfill \\
Bu = g{\text{ condition aux limites}} \hfill \\
\end{gathered} $
Ici, P représente un opérateur différentiel, u la variable dépendante (la solution), F une source, f une fonction décrivant la condition initiale, B un opérateur, et g une fonction à la frontière. La coordonnée spatiale \mathbf{x} représente l’ensemble des trois directions (x, y, et z) dans ce cas.
Le modèle mathématique peut décrire un phénomène physique tel qu’un écoulement. Dans ce cas, le modèle peut représenter la conservation de la quantité de mouvement et de la masse en temps et en espace. Heureusement, le modèle mathématique émanant de ce type de lois de conservation, complété par des valeurs initiales et des conditions aux limites adéquates, se comporte souvent très bien. Cela signifie qu’il existe une solution unique et que la solution se comporte de manière continue en fonction des données du problème; par exemple, en fonction des valeurs initiales, des termes sources ou des conditions aux limites.
Même si un problème admet une solution unique et stable, il peut être difficile voire impossible de trouver cette solution de façon analytique. Autrement dit, il peut être difficile de trouver une expression analytique pour la solution avec des opérations pouvant être facilement calculées (+, -, x, ÷). A la place, nous devons formuler un modèle numérique, qui approche le modèle mathématique. Les équations du modèle numérique peuvent être résolues à l’aide d’une méthode numérique implémentée dans un programme informatique.
Les méthodes des éléments finis et des volumes finis sont des méthodes numériques basées sur une discrétisation spatiale des équations du modèle. La discrétisation temporelle est généralement réalisée à l’aide de schémas d’intégration temporelle pour équations différentielles ordinaires. Le modèle mathématique conduit au modèle numérique suivant:
(3)
(4)
{u_h} = {f_h}{\text{ condition initiale}} \hfill \\
{B_h}{u_h} = {g_h}{\text{ condition aux limites}} \hfill \\
\end{gathered} $
où h représente un paramètre de discrétisation; par exemple, la taille de l’élément de maillage ou de la cellule dans une méthode des éléments finis ou des volumes finies, respectivement.
Notez que les éléments constitutifs d’un maillage sont appelés éléments dans les méthodes des éléments finis et cellules dans les méthodes des volumes finis.
Il y a plusieurs sources d’erreur. L’erreur de troncature, $\tau $, nous indique dans quelle mesure le modèle numérique se rapproche du modèle mathématique:
(5)
L’ordre de précision du modèle numérique nous indique la vitesse à laquelle l’erreur de troncature décroît lorsque h décroît. Cela signifie que plus la taille de l’élément ou de la cellule est petite, plus la différence entre le modèle numérique et le modèle mathématique doit devenir faible. Un modèle numérique est consistant si l’erreur de troncature décroît avec h.
L’erreur de discrétisation dans les solutions est donnée par la différence entre la solution exacte et la solution numérique aux équations du modèle:
(6)
On dit que la méthode numérique converge si la solution numérique approche la solution exacte lorsque h décroît:
(7)
L’ordre de précision de la discrétisation, p, nous indique la vitesse à laquelle la solution numérique converge vers la solution exacte lorsque h décroît.
(8)
Plus p est grand, plus vite l’approximation converge.
Existe-t-il donc une différence inhérente dans l’ordre de précision des méthodes des éléments finis et des méthodes des volumes finis? En augmentant l’ordre des fonctions de base, nous devrions en théorie atteindre n’importe quel niveau de précision avec les méthodes des éléments finis (en pratique, il y a d’autres limitations). Les méthodes d’éléments finis les plus courantes sont précises au deuxième ou au troisième ordre, et les méthodes de volumes finis sont précises au premier ou au deuxième ordre.
Quelles sont les similitudes et quelles sont les différences?
Examinons une équation de bilan de flux, qui constitue la base des modèles mathématiques pour les écoulements fluides:
(9)
Dans cette équation, u représente une quantité physique conservée, comme la quantité de mouvement ou la masse, et \Gamma représente le flux de cette quantité; par exemple, la transmission de la quantité de mouvement à travers une surface de contrôle par unité de surface et par unité de temps.
Les méthodes des éléments finis commencent par formuler une équation intégrale dans laquelle les équations sont pondérées à l’aide de fonctions tests, \varphi, et le calcul de la moyenne se fait par intégration sur le domaine du modèle:
(10)
Cependant, avant de continuer, appliquons le théorème de la divergence à \[{\Gamma \varphi }\]. Cela donne l’expression suivante:
(11)
Ici, \partial \Omega représente la frontière du domaine \Omega et \mathbf{n} représente le vecteur normal à la frontière du domaine. L’intégration par parties du membre de gauche de l’équation ci-dessus donne:
(12)
ce qui signifie que nous obtenons à partir de l’équation Eq. 11:
(13)
Nous avons donc désormais l’expression suivante:
(14)
Nous pouvons utiliser l’Eq. 14 ci-dessus pour le second terme de l’Eq. 10. Ceci afin d’inclure naturellement les conditions aux limites du flux dans les équations intégrales. Par la suite, dans l’implémentation numérique, cela présente également l’avantage que le vecteur de flux n’a pas besoin d’être différentiable. Il en résulte les équations utilisées comme point de départ dans les méthodes d’éléments finis:
(15)
C’est ce que l’on appelle la formulation faible. Le troisième terme du membre de gauche intègre le flux de u, \Gamma, sur la frontière du domaine, \partial \Omega.
La formulation faible n’est liée au modèle physique que si elle est valable pour une grande diversité de fonctions tests \varphi. Un choix courant consiste à utiliser des polynômes, mais il peut également s’agir d’autres types de fonctions. Un cas particulier est le cas d’une fonction test constante; par exemple, que \varphi = 1. La dernière équation ci-dessus, Eq. 15, donne alors:
(16)
Cette relation est utilisée comme point de départ pour les méthodes des volumes finis.
A ce stade, il n’y a pas de différence entre les méthodes des éléments finis et des volumes finis. Comme nous l’avons vu plus haut, la formulation pour les méthodes des volumes finis, l’Eq. 16, est simplement un cas particulier de la formulation faible générique utilisée dans les méthodes des éléments finis, l’Eq. 15.
La différence réside dans la discrétisation de l’Eq. 15 et de l’Eq. 16. La méthode des éléments finis est obtenue à partir de la sélection d’un nombre fini de fonctions tests \varphi = \varphi_h et nécessite que l’Eq. 15 soit valable pour chacune d’entre elles. La méthode des volumes finis est obtenue en prenant un nombre fini de volumes de contrôle \Omega = \Omega_h et nécessite que l’Eq. 16 soit valable pour chacun d’entre eux. Si l’on utilise une triangulation comme base pour ces deux méthodes, les Figures 1 et 2 montrent des formes discrétisées possibles de ces formulations éléments finis et volumes finis, respectivement.
Si nous regardons les méthodes des éléments finis les plus courantes, les fonctions tests sont non nulles uniquement aux abords de ce que l’on appelle les noeuds (fonctions de base locales). Cela signifie que les intégrales ne doivent être calculées que sur les éléments (ici, les triangles) dans ce voisinage. Regardez, par exemple, le noeud de domaine mis en évidence et les éléments dans son voisinage colorés en gris dans la Figure 1 ci-dessous. La contribution des flux de frontière, le troisième terme du membre de gauche dans l’Eq. 15, n’a besoin d’être inclus que pour les éléments ayant une face (3D) ou une arête (2D) à la frontière, puisque les contributions aux frontières interélémentaires s’annulent pour les fonctions de base continues. La Figure 1 ci-dessous montre comment l’équation pourrait être formulée pour des éléments internes du domaine (blanc, gris et vert) et pour des éléments ayant une face (3D) ou une arête (2D) sur la frontière (bleu clair). Pour le noeud mis en évidence dans la Figure 1, seuls les éléments alentour colorés en gris contribuent à l’intégrale de domaine (sur \Omega). Pour le noeud mis en évidence sur la frontière, seuls les éléments adjacents en bleu clair donnent une contribution de flux de frontière à l’intégrale sur \partial \Omega, tandis que ces deux éléments en bleu clair et l’élément en vert clair contribuent à l’intégrale de domaine (sur \Omega).
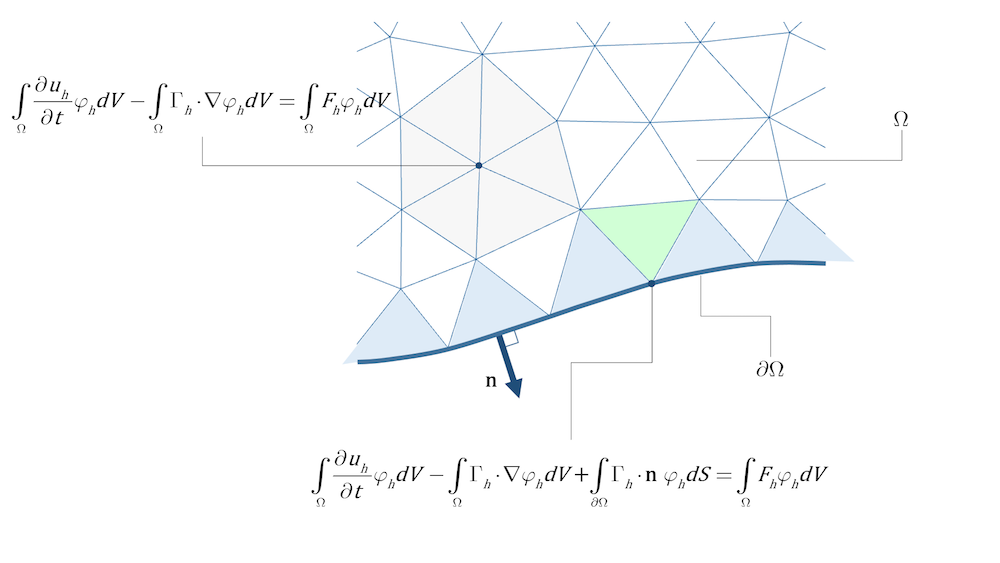
Figure 1. La contribution au domaine pour les éléments internes (blancs et gris) et pour les éléments ayant une face (3D) ou une arête (2D) sur la frontière. Le support des fonctions de base pour le noeud au milieu de l’hexagone gris est l’ensemble des éléments aux alentours; i.e. l’ensemble des éléments gris. Les fonctions de base pour les noeuds des frontières ont un support dans les éléments en bleu ciel mais aussi dans tout élément ayant un noeud sur la frontière; par exemple, l’élément vert clair. L’intégrale pour les flux a uniquement des contributions des éléments ayant une arête sur la frontière (éléments en bleu clair).
L’expression de domaine pour le flux discrétisé, \Gamma_h, s’obtient à partir des relations constitutives pour le flux; par exemple, l’équation de convection-diffusion, (le terme de diffusion dans les équations d’écoulements de fluide étant le terme visqueux du transport de la quantité de mouvement). Les expressions aux frontières pour le flux dans l’Eq. 15 sont obtenues à partir des conditions aux limites pour le modèle spécifique. Ces expressions sont ensuite incluses comme contributions pour les éléments de frontière (en bleu clair) dans la Figure 1 ci-dessus.
Si l’on considère plutôt une méthode courante de volumes finis, la méthode cell-centered, chaque cellule (triangle) est traitée comme un domaine individuel. Le terme de frontière pour le flux, le second terme du membre de gauche dans l’Eq. 16, est intégré pour toutes les cellules— à la fois les cellules internes et celles ayant une face (3D) ou une arête (2D) sur la frontière. La relation constitutive pour le flux est utilisée pour les faces ou arêtes de domaines, tandis que les conditions aux limites sont utilisées pour les faces ou arêtes sur les frontières; voir la Figure 2 ci-dessous.
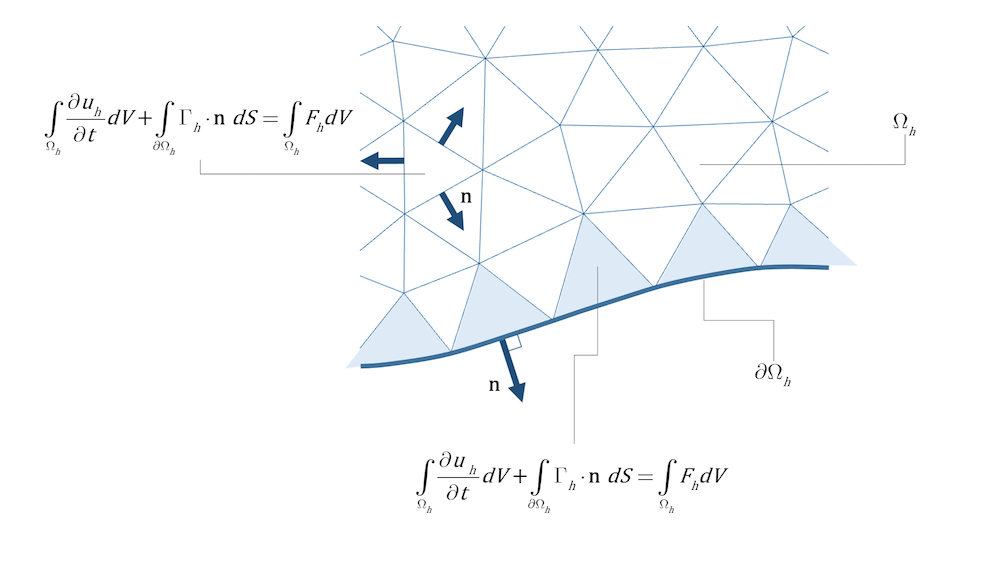
Figure 2. Le flux est intégré sur l’ensemble des faces (3D) et des arêtes (2D) des cellules, pour les cellules internes et celles ayant une face ou une arête sur une frontière.
Comment exprime-t-on alors u et \Gamma dans ces deux méthodes différentes?
Dans les méthodes des éléments finis, souvent, les mêmes fonctions de base que les fonctions tests sont utilisées pour approcher la solution. Tant que la conservation de la solution a un degré polynomial supérieur à 0 et que les dérivées d’ordre 1 peuvent être approchées, il n’y a rien de spécial à faire pour traiter un flux donné par convection et diffusion. Le vecteur flux est également une fonction polynomiale locale.
Dans les discrétisations en volumes finis, en revanche, la solution au niveau de la frontière n’est pas bien définie. La méthode ne définit que la valeur de la solution pour chaque cellule, normalement interprétée comme la valeur au centre de la cellule. Pour être utile, une méthode de volumes finis doit donc être complétée par une méthode de reconstruction. On utilise généralement une méthode d’interpolation locale dans laquelle les valeurs des cellules voisines sont prises en compte; voir la Figure 3 pour un exemple. Pour obtenir une interpolation de la solution et du flux avec un ordre supérieur, il est nécessaire de prendre en compte un plus grand nombre de valeurs de cellules. Cela n’est pas seulement compliqué, mais conduit également à une méthode moins locale.
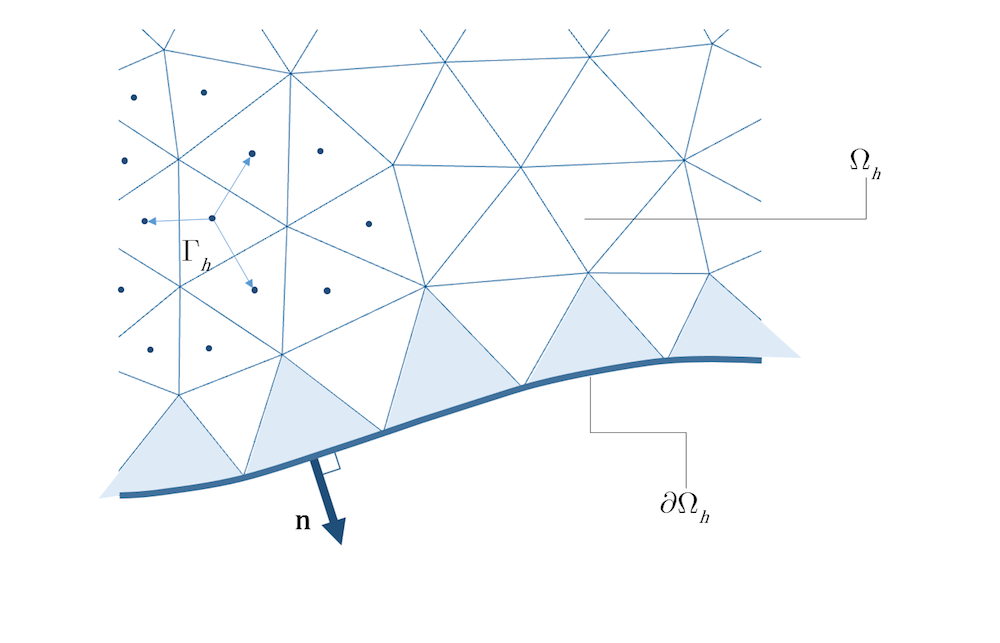
Figure 3. Dans une méthode des volumes finis cell-centered, le vecteur flux est construit par interpolation entre les points centrés dans la cellule.
Selon les fonctions de base utilisées dans une méthode des éléments finis et le type de construction du flux utilisé dans une méthode des volumes finis, des précisions différentes peuvent être obtenues. Un maillage grossier avec une méthode de précision du second ordre peut conduire à une solution plus précise qu’un maillage plus fin avec une méthode de précision du premier ordre.
Des fonctions tests et des fonctions de base linéaires pour la méthode des éléments finis conduisent généralement à des méthodes précises au second ordre. Les éléments finis présentent une grande flexibilité quant à la discrétisation. Il est plutôt simple d’utiliser des fonctions de base quadratiques par exemple. Il n’est pas non plus nécessaire de reconstruire ou d’interpoler la solution. La méthode a une nature très symétrique et les conditions aux limites de flux peuvent être imposées de façon naturelle et directe.
Un inconvénient avec la FEM est que pour des fonctions tests et de base continues, il n’y a pas de propriété de conservation locale; seule la conservation globale est assurée. En d’autres termes, seul l’équilibre du flux net à travers les frontières du domaine est assuré. Un autre inconvénient est qu’il n’y a pas de contrôle des flux locaux, ce qui signifie que la stabilisation des discrétisations pour des écoulements dominés par la convection n’est pas aisée. Stabiliser signifie, dans ce cas, retirer les oscillations non physiques qui sont des artefacts liés à la discrétisation. La conservation locale et la stabilisation des écoulements dominés par la convection peuvent être traitées en modifiant la formulation faible, directement ou indirectement. Cependant, ces méthodes peuvent être coûteuses en termes de ressources de calcul.
Comme mentionné précédemment, les méthodes des volumes finis correspondent à des fonctions de base d’éléments finis constantes par morceaux, avec potentiellement un ordre de schéma d’interpolation supérieur pour les flux. Cela conduit à des méthodes précises au premier ou au second ordre. La formulation locale des méthodes des volumes finis assure la conservation locale, ce qui en constitue une caractéristique attrayante. Cela signifie que l’équilibre du flux net de chaque cellule est garanti. Cela conduit également à des façons directes et naturelles de stabiliser le schéma de discrétisation pour les problèmes d’écoulements dominés par la convection. Les stabilisations appelées upwind et d’autres stabilisations sont naturellement obtenues en modifiant les flux aux frontières intercellules. La stabilisation upwind entraîne une non symétrie dans la discrétisation du flux convectif.
La méthode des éléments finis présente l’avantage de pouvoir formuler des méthodes pour des fonctions de base d’ordres différents. Des ordres plus élevés pour les fonctions de base donnent des méthodes précises d’ordre supérieur, qui présentent l’avantage important de pouvoir améliorer la précision pour un maillage donné. La méthode des volumes finis utilise des fonctions de base d’ordre zéro mais peut utiliser des schémas d’interpolation d’ordre supérieur pour le flux — ce qui permet également d’améliorer la précision. Lorsque l’on utilise des méthodes d’ordre supérieur, le système obtenu devient plus grand et le temps de calcul augmente pour un même maillage. Cependant, cela s’accompagne aussi d’un ordre de précision supérieur. Ainsi, lorsque l’on compare la performance, nous devons le faire pour une précision donnée. Mesurer le temps CPU et la mémoire requis pour résoudre un problème d’écoulement fluide à précision égale, avec des méthodes différentes, est la bonne façon de procéder pour comparer les performances pour ces différentes méthodes, pas le nombre de cellules ou d’éléments.
Futures méthodes des éléments finis
Chez COMSOL, nous travaillons majoritairement avec des méthodes des éléments finis pour la CFD, car c’est là que nous avons notre expertise. Ces quinze dernières années, la recherche a effectué des avancées considérables dans le développement de méthodes des éléments finis avec des fonctions tests et de base discrètes. Ce sont les méthodes DG mentionnées en introduction. Dans ces méthodes, les fonctions tests sont localisées pour chaque élément et les équations faibles sont valables pour chaque élément. La conservation locale est automatiquement obtenue et des discrétisations d’ordre supérieur sont évidentes. Il n’est pas non plus nécessaire de reconstruire la solution, excepté si l’on utilise une méthode d’ordre zéro, équivalente à la méthode des volumes finis. Le flux local à la frontière d’un élément fait naturellement partie de la formulation, ce qui signifie que la stabilisation est également directe. L’un des inconvénients des méthodes DG est le nombre relativement important de degrés de liberté supplémentaires introduits. C’est ce qui a conduit à l’étude de méthodes hybrides DG, dans lesquelles la discrétisation est plus légère et introduit moins de degrés de liberté.
Pour conclure sur la comparaison entre FEM et FVM
Comme nous l’avons vu ici, il y a des avantages et des inconvénients à la fois pour les méthodes des volumes finis et des éléments finis. De nombreux autres aspects sont importants pour un calcul efficace de problèmes d’écoulements fluides à grande échelle: gestion efficace et stable du schéma temporel; implémentation efficace de schémas d’intégration temporelle implicite, et dans une certaine mesure, explicite; résolution de grands systèmes d’équations linéaires; etc. Il y a encore beaucoup de travail et encore de nombreuses possibilités de faire progresser les différentes méthodes et technologies!
Chez COMSOL, nous nous efforçons constamment de fournir les technologies les plus efficaces et les plus récentes utilisant la méthode des éléments finis. Nous nous attachons également à développer les meilleures méthodes de façon générale — pas seulement pour la multiphysique, mais aussi pour des applications “monophysiques” telles que la CFD.




Commentaires (0)