
L’amortissement en dynamique des structures : théorie et phénomènes sources
Si vous tapez sur un bol en verre ou en métal, vous entendrez un son dont l’intensité diminue au cours du temps. Dans un monde sans amortissement, le son durerait éternellement. En réalité, il existe plusieurs phénomènes physiques par lesquels les énergies cinétique et élastique du bol se dissipent sous d’autres formes d’énergie. Dans ce blog, nous nous intéressons à la représentation de l’amortissement dans les structures vibrantes, ainsi que les phénomènes physiques qui en sont à l’origine.
Comment peut-on quantifier l’amortissement ?
Il existe plusieurs façons de décrire l’amortissement d’un point de vue mathématique. Certaines des descriptions les plus courantes sont résumées ci-dessous.
L’une des conséquences les plus évidentes d’un amortissement est la diminution de l’amplitude des vibrations libres, comme dans le cas d’un bol tibétain. Le taux de diminution dépend de l’importance de l’amortissement. Le plus souvent, l’amplitude des vibrations diminue de manière exponentielle avec le temps. C’est le cas lorsque l’énergie dissipée au cours d’un cycle est proportionnelle à l’amplitude de ce cycle.

Un bol tibétain typique. Image par Sneharamm0han — Travail personnel. Sous licence CC BY-SA 4.0, via Wikimedia Commons.
Commençons par l’équation du mouvement pour un système à un seul degré de liberté (DDL) avec amortissement visqueux et sans effort extérieur,
Après division par la masse, m, nous obtenons une équation normalisée, généralement écrite sous la forme
Ici, \omega_0 est la pulsation propre et \zeta est appelé le taux d’amortissement.
Afin que le mouvement soit périodique, le taux d’amortissement doit être compris dans l’intervalle 0 \le \zeta < 1. L’amplitude de vibration libre pour ce système diminuera par le facteur
où T0 est la période de vibration non amortie.
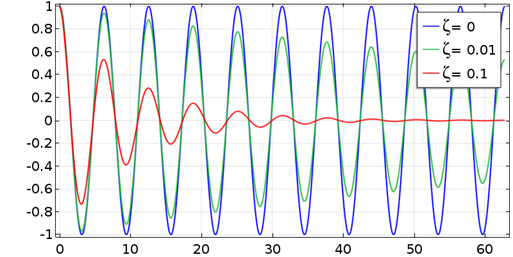
Atténuation de vibrations libres pour trois valeurs différentes de taux d’amortissement.
Une autre grandeur utilisée est le décrément logarithmique, δ. Il est défini comme le logarithme du rapport entre les amplitudes de deux pics successifs,
oùT est la période.
La relation entre le décrément logarithmique et le taux d’amortissement est
Un autre cas pour lequel l’amortissement joue un rôle important est celui d’une structure soumise à une excitation harmonique à une fréquence proche d’une fréquence propre. A résonance exacte, l’amplitude de vibration tend vers l’infini, à moins d’avoir un certain amortissement dans le système. L’amplitude réelle à résonance est contrôlée intégralement par le niveau d’amortissement.
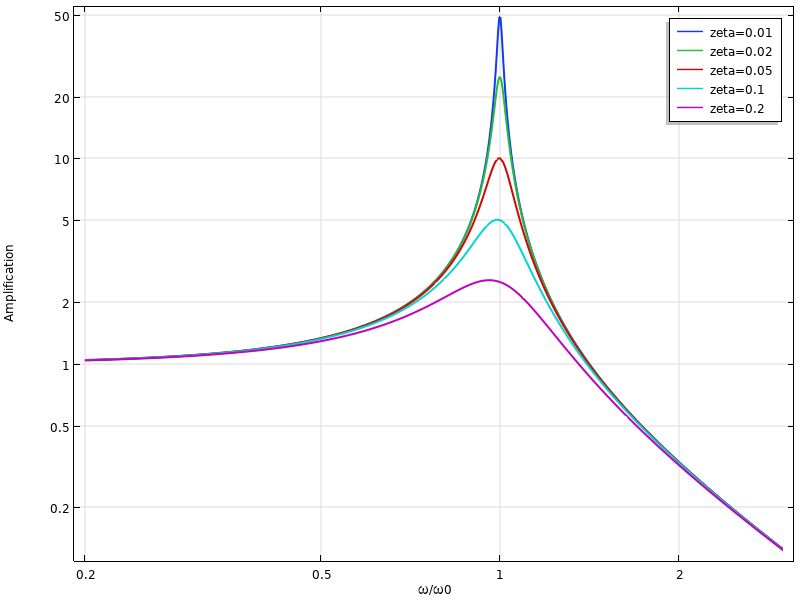
Amplification d’un système à un seul DDL pour différentes fréquences et différents taux d’amortissement.
Dans certains systèmes, comme les résonateurs, l’objectif est d’obtenir autant d’amplification que possible. Cela amène à l’utilisation d’une autre méthode courante pour mesurer l’amortissement : le facteur de qualité ou facteur Q. Il est défini comme l’amplification à résonance. Le facteur Q est lié au taux d’amortissement par la formule suivante
Un autre point de départ pour décrire l’amortissement consiste à supposer qu’il existe un certain déphasage entre la force appliquée et le déplacement résultant, ou entre la contrainte et la déformation. Parler de déphasage n’a de sens que pour les vibrations harmoniques en régime permanent. Si vous tracez le graphique de la contrainte par rapport à la déformation pour une période complète, vous verrez une ellipse décrivant un cycle d’hystérésis.
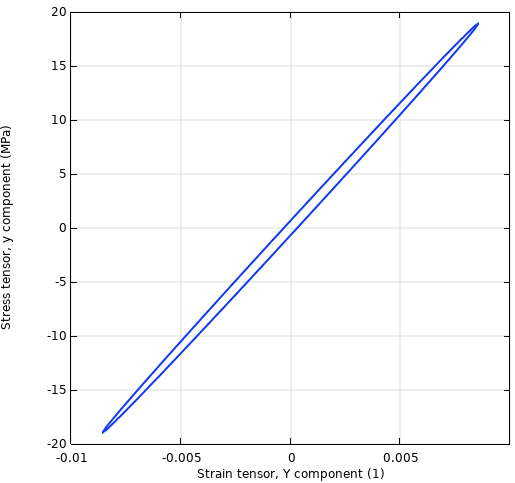
Cycle contrainte-déformation.
On peut considérer les propriétés du matériau comme étant à valeurs complexes. Ainsi, en élasticité linéaire uniaxiale, la relation contrainte-déformation en nombre complexe peut être écrite comme suit
Dans ce cas, la partie réelle du module de Young est appelée le module de stockage, et la partie imaginaire est appelée le module de perte. Souvent, le module de perte est décrit par un facteur de perte, η, de telle sorte que
E peut alors être identifié comme le module de stockage E’. Vous pouvez également trouver d’autres définitions, où E est le rapport entre l’amplitude de contrainte et l’amplitude de déformation, soit
auquel cas
La distinction est importante uniquement pour des valeurs élevées de taux d’amortissement.
Une grandeur équivalente pour estimer le facteur de perte est la tangente de perte, définie par
L’ angle de perte δ est le déphasage entre la contrainte et la déformation.
L’amortissement défini par un facteur de perte se comporte quelque peu différemment de l’amortissement visqueux. L’amortissement par facteur de perte est proportionnel à l’amplitude du déplacement, alors que l’amortissement visqueux est proportionnel à la vitesse. Il n’est donc pas possible de convertir directement une des grandeurs en l’autre.
Dans le graphique ci-dessous, la réponse d’un système à un seul DDL est comparée pour deux modèles d’amortissement. On peut voir que l’amortissement visqueux prédit un amortissement plus élevé que l’amortissement par facteur de perte au-dessus de la résonance et un amortissement plus faible en dessous de celle-ci.
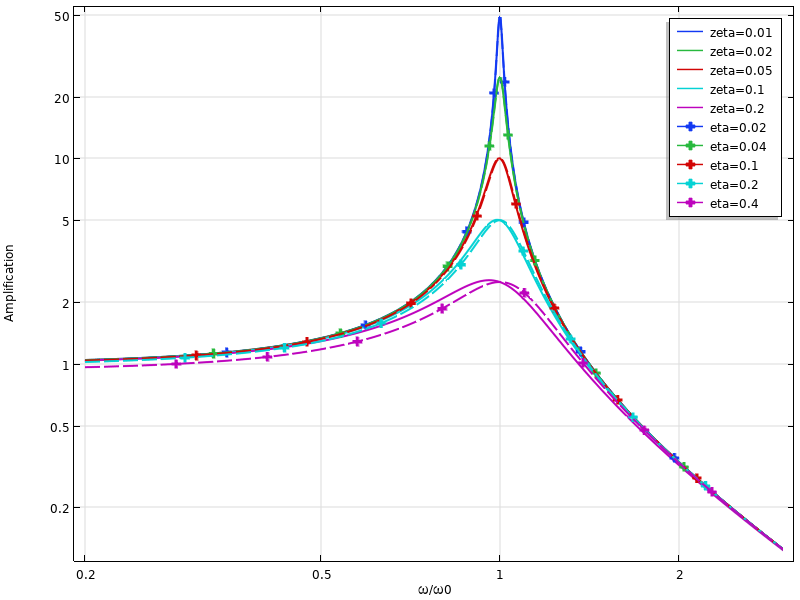
Comparaison de réponses dynamiques pour un amortissement visqueux (lignes continues) et un amortissement par facteur de perte (lignes pointillées).
Habituellement, la conversion entre le taux d’amortissement et le facteur de perte est considérée à une fréquence de résonance, ainsi \eta \approx 2 \zeta. Cependant, ceci n’est vrai qu’à une seule fréquence. Dans le graphique ci-dessous, on considère un système à deux DDL. Les valeurs d’amortissement ont été rendues équivalentes à la première fréquence de résonance, et on visualise clairement que les prédictions pour la seconde résonance diffèrent de manière significative.
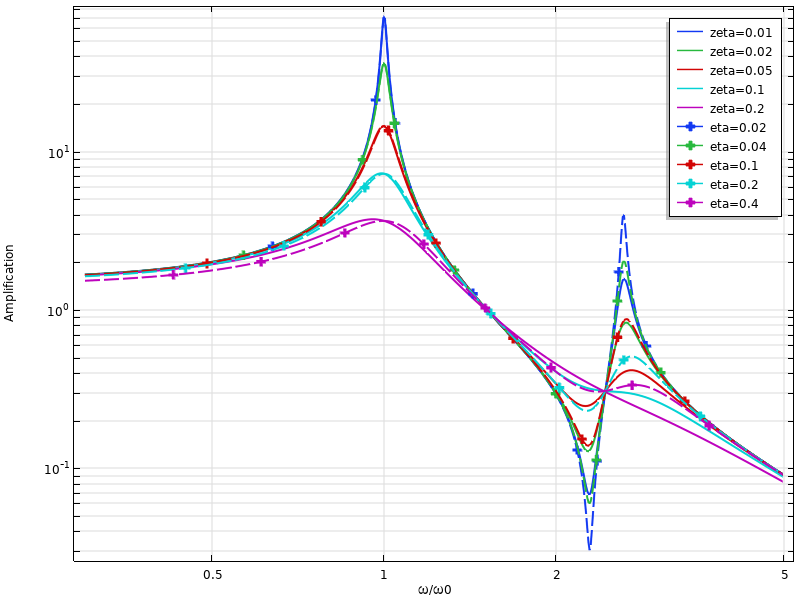
Comparaison des réponses dynamiques d’un amortissement visqueux et d’un amortissement par facteur de perte pour un système à deux DDL.
Le principe de facteur de perte peut être généralisé en définissant ce facteur de perte en termes d’énergie. On peut montrer que pour la loi de comportement matériau décrite précédemment, l’énergie dissipée pendant un cycle de charge est égale à
où \varepsilon_a est l’amplitude de déformation.
De même, l’énergie élastique maximale au cours du cycle correspond à
Le facteur de perte peut alors être écrit en termes d’énergie avec l’expression suivante
Cette définition en termes d’énergie dissipée peut être utilisée indépendamment du fait que la courbe d’hystérésis corresponde à une parfaite ellipse ou non — tant que les deux quantités d’énergie peuvent être déterminées.
Sources d’amortissement
D’un point de vue physique, il existe de nombreuses sources d’amortissement possibles. La nature a toujours tendance à trouver un moyen de dissiper l’énergie.
Pertes intrinsèques au matériau
Tous les matériaux réels dissipent de l’énergie lorsqu’ils sont soumis à une déformation. On peut considérer cela comme la conséquence des frottements internes au matériau. Si on examine une courbe contrainte-déformation pour un cycle de charge complet, elle ne décrira pas une ligne parfaitement droite. On observera plutôt une forme ressemblant à une ellipse mince.
Souvent, l’amortissement par facteur de perte est considéré comme une représentation appropriée pour l’amortissement des matériaux, car l’expérience montre que la dissipation d’énergie par cycle tend à ne pas trop dépendre de la fréquence et l’amplitude. Cependant, puisque la formulation mathématique de l’amortissement par facteur de perte est basée sur des grandeurs à valeurs complexes, l’hypothèse sous-jacente est que les vibrations sont harmoniques. Ainsi, ce modèle d’amortissement ne peut être utilisé que pour des analyses dans le domaine fréquentiel.
Le facteur de perte d’un matériau peut varier significativement, en fonction de sa composition exacte et des références consultées. Le tableau ci-dessous présente quelques estimations approximatives.
| Matériau | Facteur de perte, η |
|---|---|
| Aluminum | 0.0001–0.02 |
| Béton | 0.02–0.05 |
| Cuivre | 0.001–0.05 |
| Verre | 0.0001–0.005 |
| Caoutchouc | 0.05–2 |
| Acier | 0.0001–0.01 |
Les facteurs de perte ainsi que toutes représentations similaires de l’amortissement sont principalement utilisés lorsque la physique exacte de l’amortissement dans le matériau est inconnue ou n’est pas importante. Pour plusieurs lois de comportement, notamment pour la viscoélasticité, la dissipation est une propriété inhérente du modèle.
Frottements dans les assemblages
Il est courant d’assembler des structures par l’intermédiaire, entre autres, de boulons ou de rivets. Si les surfaces assemblées glissent les unes par rapport aux autres lors de vibrations, l’énergie est dissipée par frottement. Tant que la valeur de la force de frottement elle-même ne varie pas au cours du cycle, l’énergie dissipée par cycle est plus ou moins indépendante de la fréquence. En ce sens, ce frottement est similaire à la dissipation interne du matériau.
Les assemblages vissés sont courants en génie mécanique. La quantité de dissipation qui se manifeste dans ces assemblages peut varier considérablement en fonction de leur conception. Si la dissipation doit être faible, les boulons doivent être suffisamment rapprochés et serrés afin d’empêcher tout glissement macroscopique entre les surfaces assemblées.
Emission sonore
Une surface vibrante déplace l’air ambiant (ou tout autre milieu environnant), générant ainsi des ondes acoustiques. Ces ondes emportent une certaine quantité d’énergie, ce qui résulte en une dissipation d’énergie du point de vue de la structure.

Graphique du rayonnement acoustique d’un transducteur Tonpilz.
Pertes d’ancrage
Souvent, un composant de petite dimension est fixé à une structure plus grande qui ne fait pas partie de la simulation. Lorsque le composant vibre, certaines ondes sont induites dans la structure de soutien et se propagent. Ce phénomène est souvent appelé pertes d’ancrage (anchor losses), notamment dans le cadre des MEMS.
Amortissement thermoélastique
Même en cas de déformation élastique pure sans dissipation, la déformation d’un matériau modifie légèrement sa température. Un étirement local entraîne une diminution de la température, tandis qu’une compression provoque un échauffement local.
Fondamentalement, il s’agit d’un processus réversible, de sorte que la température reviendra à sa valeur initiale si la contrainte est relâchée. Cependant, on observe généralement des gradients dans le champ de contraintes, associés à des gradients de température. Ces gradients provoquent un flux de chaleur des régions chaudes vers les régions froides. Lorsque la contrainte est relaxée suite à un cycle de charge, la distribution de température n’est plus la même que celle existant lors de la mise en charge. Il n’est donc pas possible de revenir localement à l’état initial. Ce phénomène devient une source de dissipation.
L’amortissement thermoélastique est surtout important lorsque l’on travaille sur des petites échelles de longueur et des vibrations à haute fréquence. Pour les résonateurs MEMS, l’amortissement thermoélastique peut entraîner une diminution significative du facteur de qualité Q.
Amortisseurs
Parfois, une structure comporte des amortisseurs visqueux placés de façon intentionnelle, tel que l’amortisseur d’une suspension de véhicule.
 Amortisseurs. Image par Avsar Aras — Travail personnel. Sous licence CC BY-SA 3.0, via Wikimedia Commons.
Amortisseurs. Image par Avsar Aras — Travail personnel. Sous licence CC BY-SA 3.0, via Wikimedia Commons.
De tels composants ont bien entendu une forte influence sur l’amortissement total d’une structure, au moins pour certains modes de vibration.
Amortisseurs parasismiques
Un domaine particulier dans lequel on consacre d’importantes ressources pour l’amortissement est celui du génie civil dans les zones sismiques actives. Il est primordial de réduire les niveaux de vibration dans les bâtiments s’ils sont sujets à un tremblement de terre. L’objectif de ces amortisseurs peut être à la fois d’isoler une structure par rapport à ses fondations et d’apporter suffisamment de dissipation.

Amortisseur parasismique d’un bâtiment municipal. Image par Shustov — Travail personnel. Sous licence CC BY-SA 3.0, via Wikimedia Commons.
Lecture complémentaire
Accédez aux suites de ce blog ci-dessous:




Commentaires (0)