Structure et acoustique Articles de Blog

Maximiser les fréquences propres grâce à l’optimisation de forme et l’optimisation topologique
La résonance mécanique peut causer des problèmes de fatigue dans les machines. Découvrez comment limiter les problèmes de résonance avec l’optimisation de forme et l’optimisation topologique.

Réponse impulsionnelle acoustique d’une enceinte intelligente à l’intérieur d’une pièce
La réponse acoustique d’une enceinte intelligente peut être modélisée à l’aide d’un couplage MEF–rayons disponible dans le logiciel COMSOL Multiphysics®. Pour en savoir plus, cliquez ici.

Développer de meilleurs résonateurs pour la technologie CMOS
Les technologies sub-GHz sont utilisées en masse pour la domotique, la surveillance des infrastructures, etc. Cette demande croissante nécessite de disposer de filtres et de résonateurs RF conçus de manière optimale.
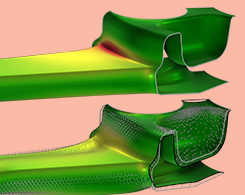
Minimisation des contraintes: une approche heuristique pour améliorer le comportement en fatigue
2 modèles, un bracket et une jante, illustrent une méthode d’optimisation par gradient permettant d’utiliser une minimisation des contraintes de manière heuristique pour améliorer le comportement en fatigue.

Comment évaluer les contraintes dans COMSOL Multiphysics® ?
Une introduction complète à l’évaluation de diverses grandeurs de contraintes dans COMSOL Multiphysics®.

Simulation des accéléromètres et des gyroscopes MEMS utilisés dans les unités de mesure inertielle
De nombreux véhicules autonomes s’appuient sur des IMUs pour la navigation. Nous montrons ici comment le module MEMS peut vous aider à modéliser les gyroscopes et les accéléromètres utilisés dans les IMU.
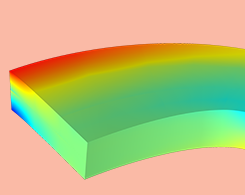
Quelle est la différence entre contraintes planes et déformations planes?
Nous passons en revue les formulations et les modèles constitutifs que vous pouvez utiliser pour étudier les contraintes planes, les déformations planes et les déformations planes généralisées dans vos problèmes de mécanique du solide.
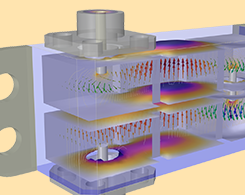
Conception de filtres à cavité pour les dispositifs 5G grâce à la modélisation multiphysique
Des radars aux fours à micro-ondes en passant par les accélérateurs de particules, les filtres à cavité RF sont présents dans de nombreux domaines d’application différents. Parmi eux : les appareils et infrastructures 5G.
