
Tout ingénieur en mécanique des structures utilise le principe de Saint-Venant, qu’il en soit conscient ou non. La plupart des manuels de mécanique des structures contiennent diverses formulations de ce principe, mais sa signification exacte n’est pas évidente. Le principe de Saint-Venant nous dit qu’à une certaine distance d’une zone soumise à un chargement, la distribution exacte du chargement n’a pas d’importance du moment que les résultantes de celui-ci sont correctes. Dans cet article de blog, nous allons explorer le principe de Saint-Venant, en particulier dans le contexte d’analyses éléments finis (EF).
L’histoire du principe de Saint-Venant
Le scientifique français Barré de Saint-Venant a formulé son célèbre principe en 1855, bien qu’il s’agisse plus d’une observation que d’un énoncé mathématique:
“Si les forces agissant sur une petite partie de la surface d’un corps élastique sont remplacées par un ensemble de forces statiquement équivalent agissant sur la même portion de la surface, cette redistribution de chargement entraîne des modifications substantielles des contraintes locales, mais a un effet négligeable sur les contraintes à des distances qui sont grandes par rapport aux dimensions linéaires de la surface sur laquelle les forces sont modifiées.”
B. Saint-Venant, Mém. savants étrangers, vol. 14, 1855.

Portrait de Saint-Venant. Image dans le domaine public, via Wikimedia Commons.
D’autres grands esprits du domaine de la mécanique appliquée — Boussinesq, Love, von Mises, Toupin, et d’autres — ont participé à l’énonciation d’une formulation plus exacte du principe de Saint-Venant, et à en fournir des démonstrations mathématiques. Cela s’avère assez difficile pour des cas plus généraux, ce qui en fait toujours un sujet de recherches. (Le débat a parfois été très vif.)
Un exemple simple: analyser les contraintes à une certaine distance
Commençons par quelque-chose de relativement simple: une fine plaque rectangulaire comportant un perçage circulaire à une certaine distance de l’arête chargée, sur laquelle on tire dans la direction axiale. Si nous nous intéressons à la concentration de contraintes au niveau du trou, quelle est l’influence de la distribution réelle du chargement?
Trois types de chargement sont appliqués sur la frontière à l’extrémité droite:
- Une contrainte axiale constante de 100 MPa
- Une distribution parabolique symétrique de la contrainte appliquée avec une amplitude maximale de 150 MPa
- Un chargement ponctuel ayant la même résultante que les deux cas de chargement précédents
Comme on peut le voir sur les graphiques ci-dessous, la répartition de la contrainte au niveau du trou n’est pas influencée par la façon dont le chargement est appliqué. La raison ici, bien sûr, est que le trou est situé suffisamment loin du chargement.

Isovaleurs des contraintes de Von Mises pour les trois cas de chargement.
Une autre façon de visualiser ce scénario est d’utiliser des flèches représentant la contrainte principale. Ce type de graphique représente le champ de contrainte comme un flux et donne une bonne idée de la redistribution.
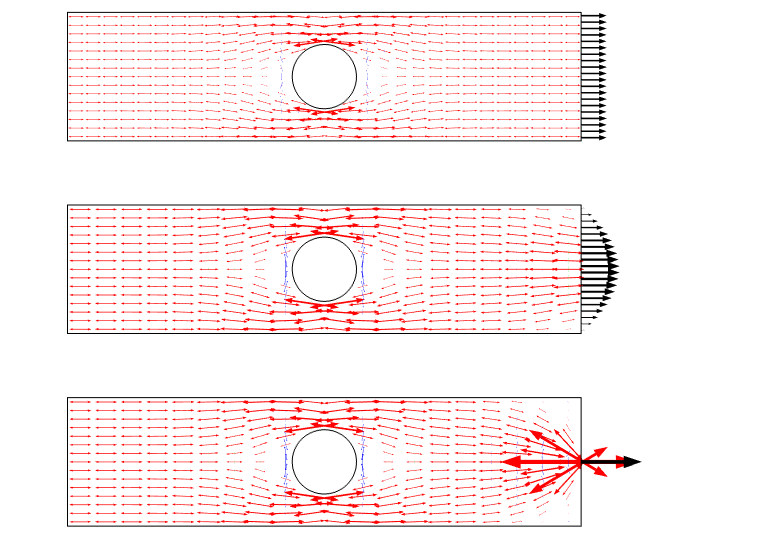
Graphique de la contrainte principale pour les trois cas de chargement. On note une singularité lorsqu’un chargement ponctuel est utilisé.
En traçant la contrainte le long d’une ligne, on peut voir que les trois cas de chargement convergent les uns vers les autres à une certaine distance de la frontière, qui est approximativement égale à la largeur de la plaque.
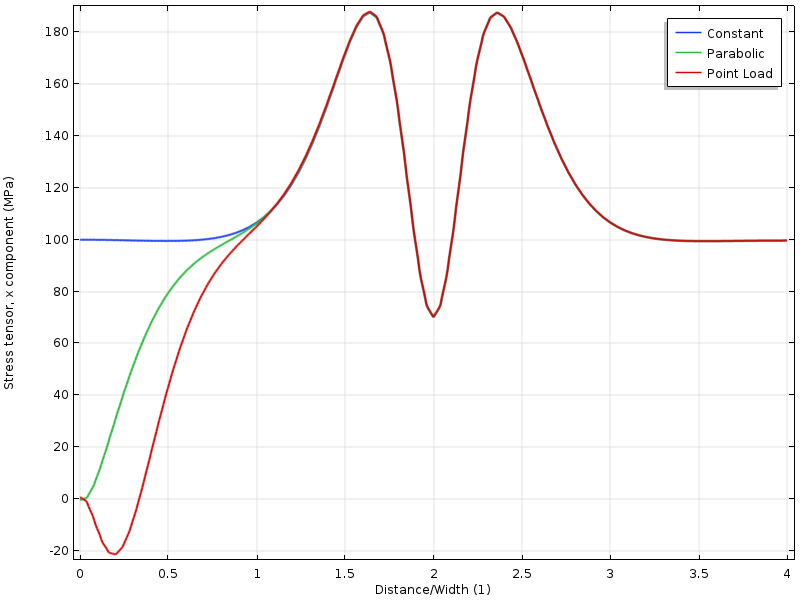
Contrainte le long de la frontière supérieure en fonction de la distance depuis la frontière chargée. La distance est normalisée par la largeur de la plaque.
Si l’on rapproche le trou de la frontière chargée, la situation change. L’état de contrainte autour du trou dépend cette fois de la distribution du chargement. Un élément encore plus intéressant est que désormais, la distance à partir de laquelle les trois champs de contraintes sont identiques est deux fois plus éloignée de la frontière chargée. L’application du principe de Saint-Venant implique que les contraintes sont libres de se redistribuer. Dans ce cas, la redistribution est partiellement bloquée par le trou.
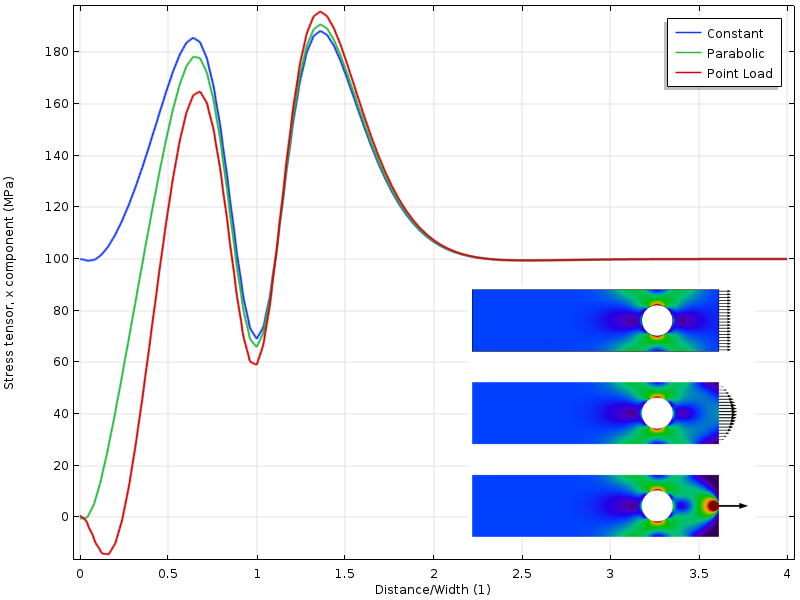
Contrainte le long de la frontière supérieure avec le trou plus proche de la frontière chargée.
Notez que le principe de Saint-Venant nous dit qu’il n’y a pas de différence de l’état de contraintes à une distance qui est de l’ordre de la dimension linéique de la zone chargée. La zone chargée à prendre en compte, cela dit, n’est pas forcément la zone réelle de chargement! Cela peut sembler étrange, mais on peut le voir de cette façon: quand le trou est éloigné, on peut calculer un facteur de concentration de contrainte en utilisant un manuel (le mien indique 4.32) plutôt qu’en utilisant une solution EF. L’approche du manuel s’appuie sur une hypothèse implicite selon laquelle le chargement est distribué de façon uniforme, comme pour le premier cas de chargement. Donc même si le chargement réel était uniquement appliqué sur une petite partie de la frontière, la distance critique serait liée à la taille de la frontière complète.
En résolvant le problème à l’aide de la méthode des éléments finis (MEF), le trou peut être arbitrairement proche du chargement. La limite est que d’un point de vue physique la distribution du chargement soit bien définie. Dès lors que l’on fait une hypothèse sur la répartition des contraintes, néanmoins, cela suggère une hypothèse implicite sur la distribution du chargement, qui pourrait différer de celle réellement appliqué.
Systèmes à résultante nulle et densité d’énergie de déformation
Jusqu’ici, nous avons dit que les contraintes sont les mêmes quels que soient les détails du chargement à une distance suffisante. Puisqu’il s’agit ici d’élasticité linéaire, nous pouvons toujours superposer les cas de chargement. Lorsque l’on travaille avec le principe de Saint-Venant, il est plus facile de formuler un principe dans ce sens: les contraintes résultant d’un chargement n’ayant aucune force ou moment résultant seront faibles à une distance du même ordre de grandeur que la taille de la frontière chargée.
Nous allons donc étudier la contrainte causée par la différence entre deux chargements ayant des résultantes égales. La plupart des démonstrations modernes sont basées sur des estimations de la décroissance de la densité d’énergie de déformation pour un système à résultante nulle.
En revenant au problème ci-dessus, nous pouvons calculer la différence entre les cas de chargement. Cela nous permettra d’analyser la décroissance réelle de la contrainte ou de la densité d’énergie de déformation pour la différence des champs de contraintes.
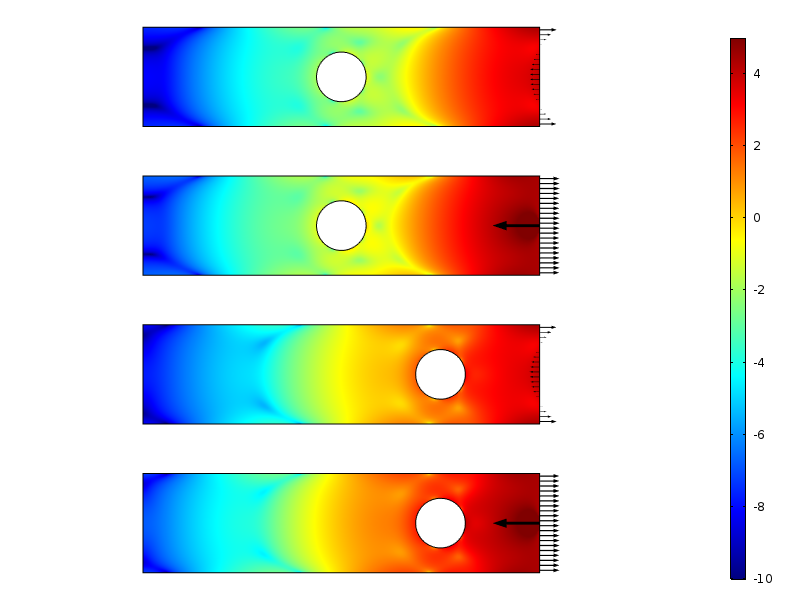
Logarithme de la densité d’énergie de déformation pour les cas de chargement à résultante nulle.
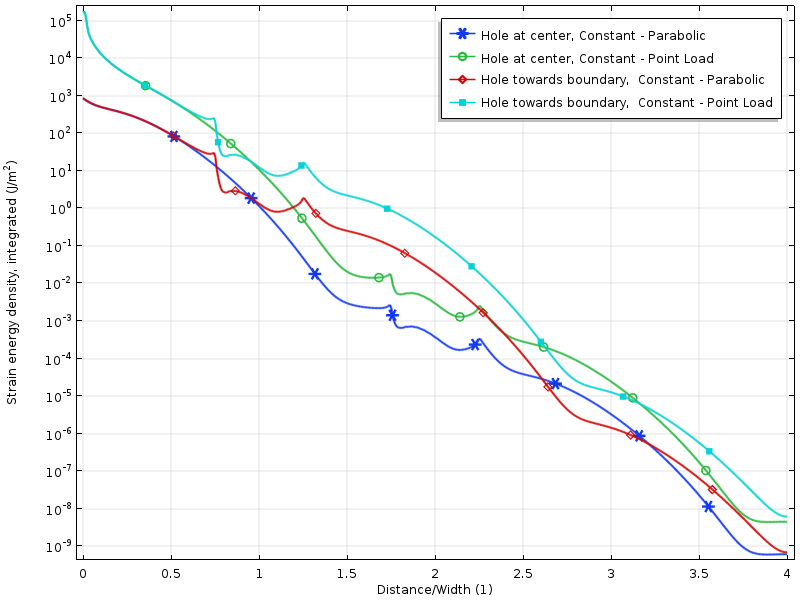
La densité d’énergie de déformation le long de la plaque pour des chargements à résultante nulle. L’énergie est intégrée selon la direction verticale afin de générer une quantité qui varie seulement avec la distance au chargement.
La décroissance du logarithme de la densité d’énergie de déformation est plus ou moins linéaire avec la distance à la paroi chargée. C’est en phase avec ce que les démonstrations récentes prédisent: une décroissance exponentielle de la densité d’énergie de déformation. On peut également observer comment le trou réduit temporairement le taux de décroissance.
Application du principe de Saint-Venant à des structures minces
Pour des structures plus minces telles que les coques, poutres et treillis, il est bien connu que le principe de Saint-Venant ne peut pas être appliqué de la même façon que pour des objets plus “solides”. Les perturbations se propagent sur des distances plus importantes que prévues, car les directions de propagation des contraintes pour une structure mince sont bien plus limités. Il s’agit du même phénomène que celui observé avec le trou dans l’exemple ci-dessus, mais de manière plus prononcée.
Intéressons-nous à une poutre de section standard IPE100. L’extrémité de la poutre est soumise à un chargement axial, avec une amplitude ayant une distribution linéaire dans les deux directions transverses.
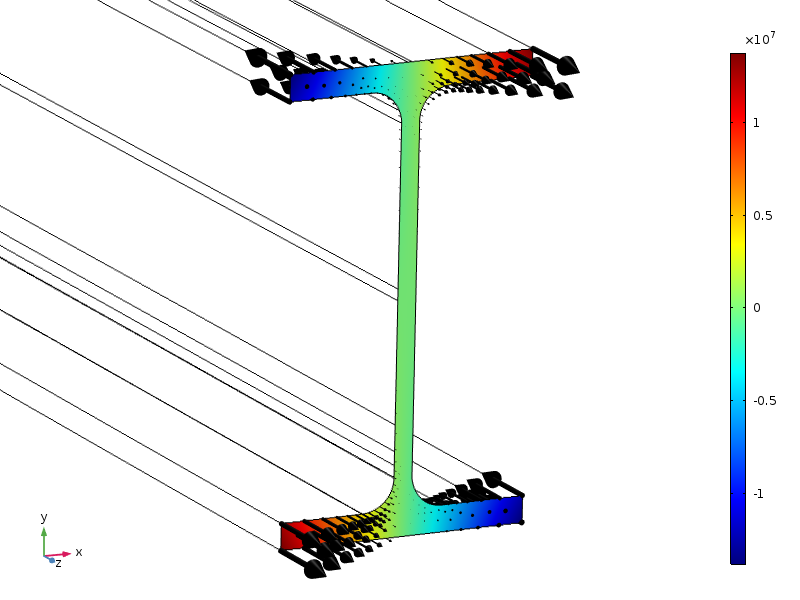
Distribution du chargement, affichée au niveau de la section et sous forme de flèches.
Du fait des symétries, ce chargement présente une force résultante nulle, ainsi qu’un moment nul autour de l’ensemble des axes. La section a une hauteur de 100mm, donc si la formulation standard du principe de Saint-Venant est applicable, les contraintes devraient être faibles à une distance d’environ 100mm de l’extrémité.
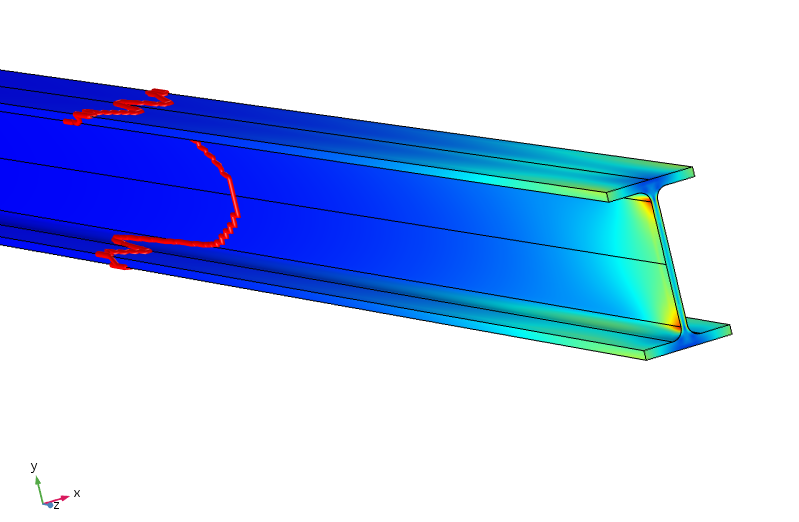
Contrainte équivalente dans une poutre. L’isovaleur rouge indique l’endroit à partir duquel la contrainte est inférieure à 5% de la contrainte maximale appliquée.
Pour obtenir une contrainte inférieure à 5% de la contrainte maximale appliquée, il faut se déplacer de presque un mètre le long de la poutre. La répartition des contraintes est donc beaucoup moins efficace, étant donné que l’équilibre entre les brides supérieure et inférieure nécessite un transfert de moment à travers l’âme fine.
Si vous êtes familier avec la théorie de la torsion non uniforme des poutres (i.e. théorie du gauchissement, ou théorie de Vlasov), vous constaterez que le chargement appliqué a un bimoment significatif. Le bimoment est une quantité de la section ayant pour dimension physique force X longueur2.
Peut-être (c’est juste une spéculation personnelle), qu’un principe de Saint-Venant adapté à ce cas requerrait non seulement une force et un moment mais aussi un bimoment nuls. Il faudrait pour cela ajouter quatre chargements ponctuels qui fourniraient un bimoment opposé. Le résultat de cette analyse est présenté ci-dessous.
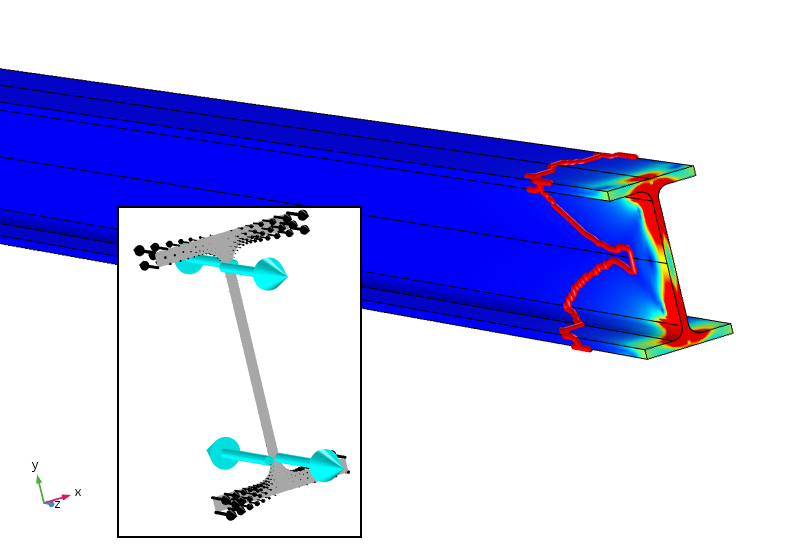
Contrainte équivalente avec quatre chargements ponctuels dont le bimoment opposé à celui du chargement initial. La limite de la contrainte à 5% de la contrainte maximale appliquée est désormais plus proche de la frontière chargée.
Les chargements ponctuels appliqués, qui ne sont délibérément pas positionnés de façon optimale, entraînent des contraintes locales très hautes (en réalité singulières). Cela dit, la contrainte décroit bien plus rapidement et passe en dessous de 5% après environ 100mm. La limite de 5% est toujours indiquée par rapport au chargement distribué appliqué, elle n’est donc pas ajustée aux nouvelles contraintes locales. La décroissance logarithmique de la densité d’énergie de déformation est trois fois plus rapide une fois que les chargements ponctuels ont été ajoutés.
Le principe de Saint-Venant en analyse par éléments finis
Dans certains cas, vous pouvez intuitivement considérer que le principe de Saint-Venant est applicable au problème EF discrétisé. Examinons les chargements distribués et les maillages non conformes.
Chargements distribués
Dans le modèle EF, les chargements sont toujours appliqués aux noeuds du maillage, même si vous les définissez comme un chargement sur frontière continu. Le chargement est réparti en interne sur les noeuds des éléments en utilisant le principe des travaux virtuels, comme vous pouvez le voir dans l’exemple ci-dessous.
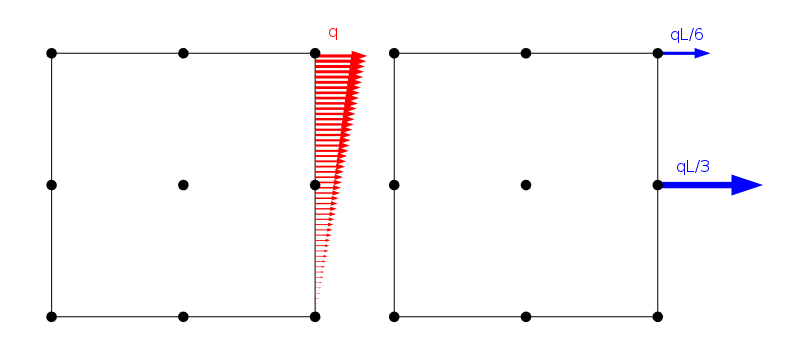
Un chargement distribué linéairement et la façon dont il est appliqué sur les noeuds d’un élément de Lagrange d’ordre deux et de dimension L.
Il y a cependant un nombre infini de répartitions de chargement qui donneront les mêmes chargements nodaux tant qu’ils partagent les mêmes forces et moments résultants. La solution du modèle en éléments finis sera évidemment la même pour l’ensemble de ces cas de chargement. A partir du principe de Saint-Venant, néanmoins, on peut conclure que tous ces chargements donneraient sensiblement les mêmes résultats du moment que l’on se place à une certaine distance.
La taille de la zone sur laquelle on répartit le chargement étant la surface d’un élément, la dimension linéique au-delà de laquelle il n’y a pas de différence correspond globalement à une couche d’éléments à l’intérieur de la structure. La solution dans la couche d’éléments la plus extérieure ne correspond donc pas exactement au véritable chargement, mais lorsque l’on regarde plutôt vers l’intérieur, c’est le cas.
Appliquons par exemple un effort sur une plaque rectangulaire avec un chargement sur frontière dont la contrainte présente une distribution exponentielle. La contrainte calculée avec un maillage fin est présentée ci-dessous.

Graphique d’isovaleurs de la distribution de la contrainte axiale.
Du fait du principe de Saint-Venant, le champ de contrainte est réparti comme un état de flexion pure à une certaine distance de la frontière chargée, comme on pourrait s’y attendre. Ce n’est cependant pas le sujet de cette discussion. Nous allons plutôt analyser la différence entre la distribution de contrainte ci-dessus, et ce que nous obtenons avec des maillages grossiers.
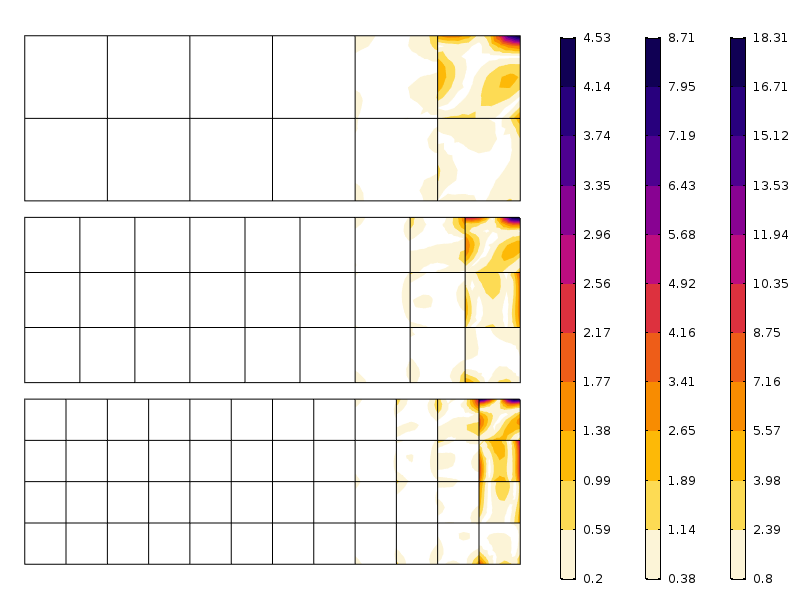
Erreur de la contrainte axiale pour trois maillages différents. Notez les échelles différentes. Comme attendu, l’erreur est plus faible lorsque le maillage est plus fin.
Comme vous pouvez le voir sur l’image, l’erreur décroît rapidement après la première couche d’éléments. Ce que nous observons ici est en fait un effet combiné de convergence en maillage et de répartition des contraintes liées au principe de Saint-Venant.
Maillage non conforme
Un maillage non conforme apparaît lorsque les fonctions de forme de deux éléments connectés ne correspondent pas. Le cas le plus commun est celui d’un assemblage connecté via des paires d’identité et des conditions de continuité. Pour illustrer cela, étudions un barreau droit ayant un maillage volontairement non conforme. Avec un cas de chargement simple, comme de la traction uniaxiale, on peut étudier les perturbations de la contrainte résultant de la transition.
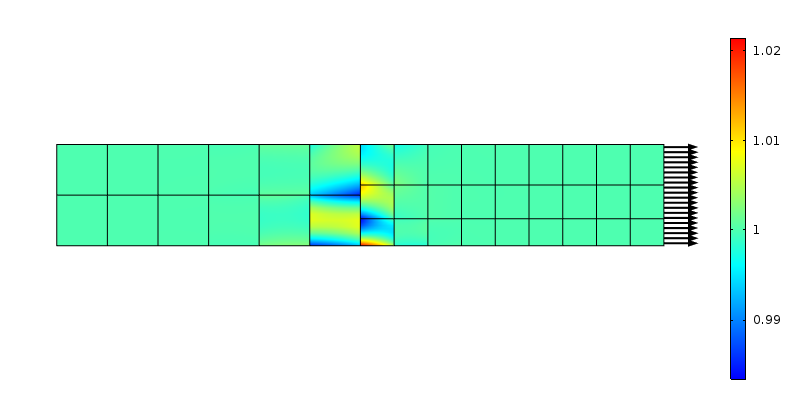
Contrainte axiale à la transition d’un maillage non conforme. Des éléments d’ordre deux sont utilisés.
Les efforts transmis par les noeuds des deux côtés ne concordent pas avec l’hypothèse d’une contrainte constante. Cela peut être vu comme une redistribution locale des chargements sur une zone correspondant à la taille d’un élément. En suivant le raisonnement de Saint-Venant, la perturbation devrait disparaître à une distance “d’un élément” de la transition. Regardons ce qu’il se passe si le maillage est raffiné dans la direction axiale.
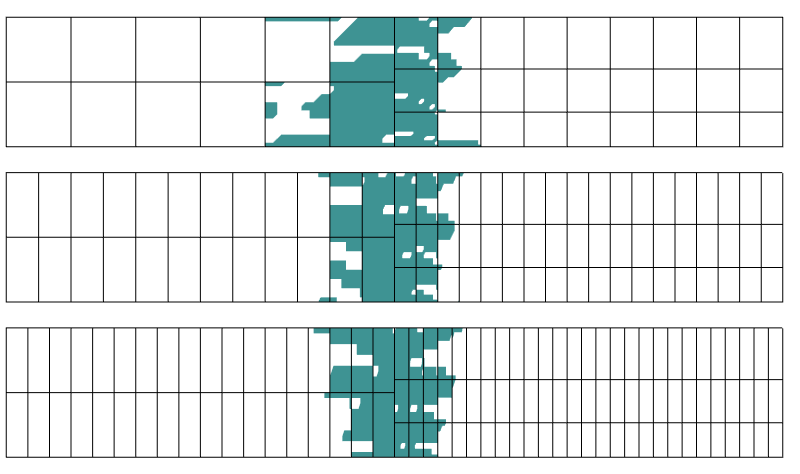
Zones dans lesquelles l’erreur sur la contrainte dépasse 0.1%. Trois discrétisation différentes dans la direction axiale sont utilisées.
Il s’avère que la région de la perturbation n’est pas vraiment affectée par la discrétisation dans la direction perpendiculaire à la frontière de transition. C’est exactement ce que le principe de Saint-Venant nous dit.
Conclusions
Sans utiliser le principe de Saint-Venant, de nombreuses analyses structurelles seraient difficiles à mener, tout simplement car la répartition détaillée des chargements n’est pas connue.
Le principe n’est formellement valide que pour des matériaux élastiques linéaires. En pratique, on peut également l’utiliser au quotidien pour d’autres situations. A titre d’exemple, si le matériau de l’exemple de “plaque trouée” était élastoplastique, on pourrait s’attendre à ce que les deux chargements distribués donnent des résultats équivalents, tant que la limite d’élasticité est supérieure à la contrainte appliquée à la frontière, de sorte qu’il n’y ait une déformation plastique qu’autour du trou. Le chargement ponctuel, cependant, donnera toujours une solution différente, étant donné que le matériau plastifie autour du point sur lequel le chargement est appliqué. Une discussion plus détaillée est présentée dans l’ article de blog sur les singularités au niveau des chargements ponctuels.
Etapes suivantes
Apprenez en plus sur l’utilisation de COMSOL Multiphysics® en FEA.
Pour en savoir plus
- Y.C. Fung and P. Tong, Classical and Computational Solid Mechanics, World Scientific Publishing Co. Pte. Ltd., 2001.



Commentaires (0)