Menu

Module Uncertainty Quantification

Comprendre et caractériser les incertitudes des modèles

Le module Uncertainty Quantification est utilisé pour comprendre l'impact de l'incertitude d'un modèle — comment les quantités d'intérêt dépendent des variations des entrées d'un modèle. Il fournit une interface générale pour le screening, l'analyse de sensibilité, la propagation des incertitudes et l'analyse de fiabilité.

Le module Uncertainty Quantification permet de tester efficacement la validité des hypothèses du modèle, de simplifier les modèles de manière convaincante, de comprendre les principales entrées des quantités d'intérêt, d'explorer la distribution de probabilité des quantités d'intérêt et d'évaluer la fiabilité d'une conception. L'assurance de l'exactitude du modèle et la compréhension accrue des quantités d'intérêt contribuent à réduire les coûts de production, de développement et de fabrication.

Le module Uncertainty Quantification peut être utilisé avec l'ensemble des produits de la gamme COMSOL pour analyser les incertitudes dans les simulations en électromagnétisme, mécanique des structures, acoustique, CFD, thermique et en génie chimique. Vous pouvez le combiner avec le module CAD Import, le module Design ou tout autre produit LiveLink™ pour la CAO.

Contacter COMSOL
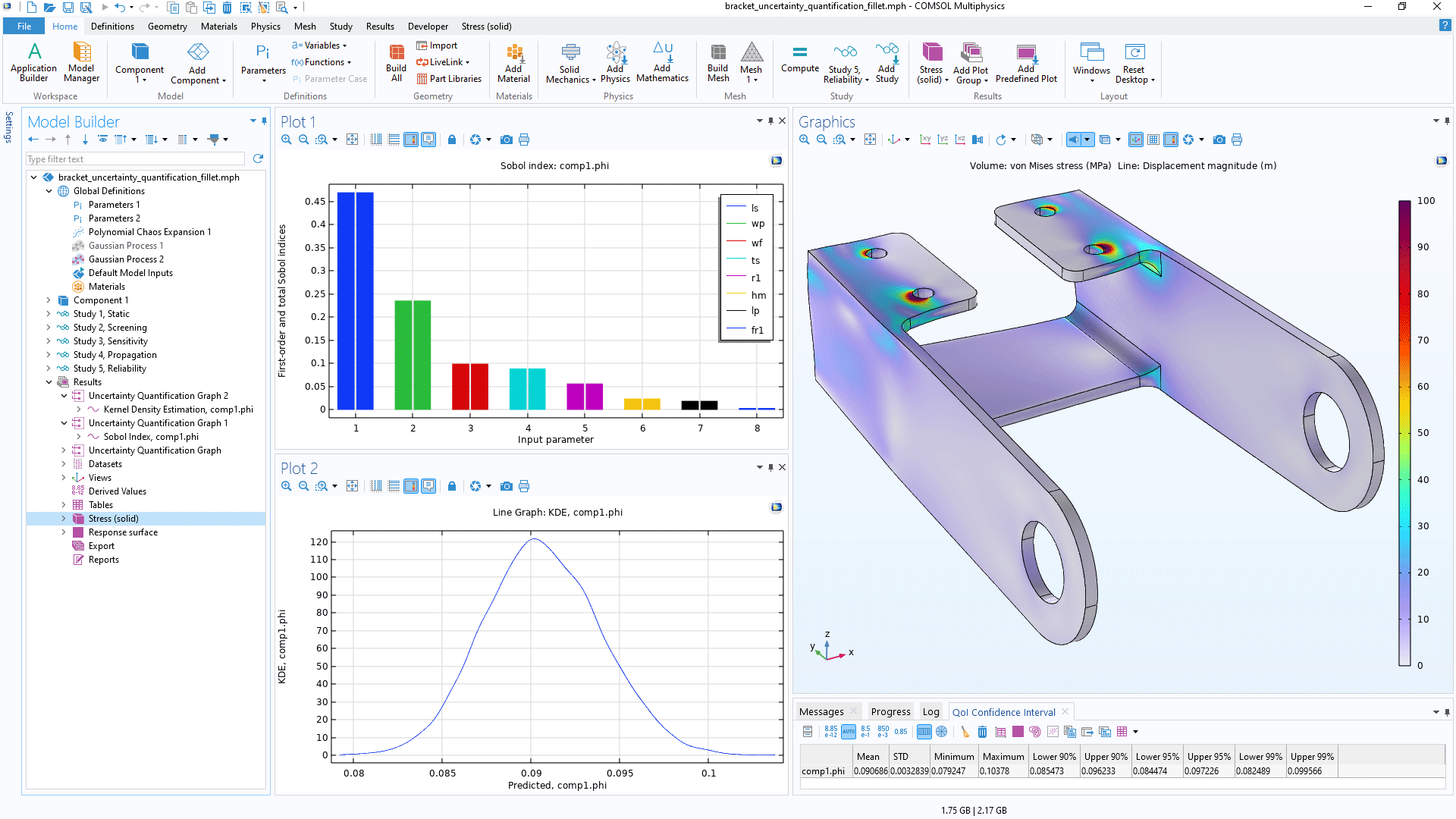
L'interface utilisateur de COMSOL Multiphysics montrant certains résultats de l'étude de quantification des incertitudes, avec un graphique d'indices de Sobol, un graphique d'estimation de la densité du noyau, ainsi qu'un tableau d'intervalle de confiance.
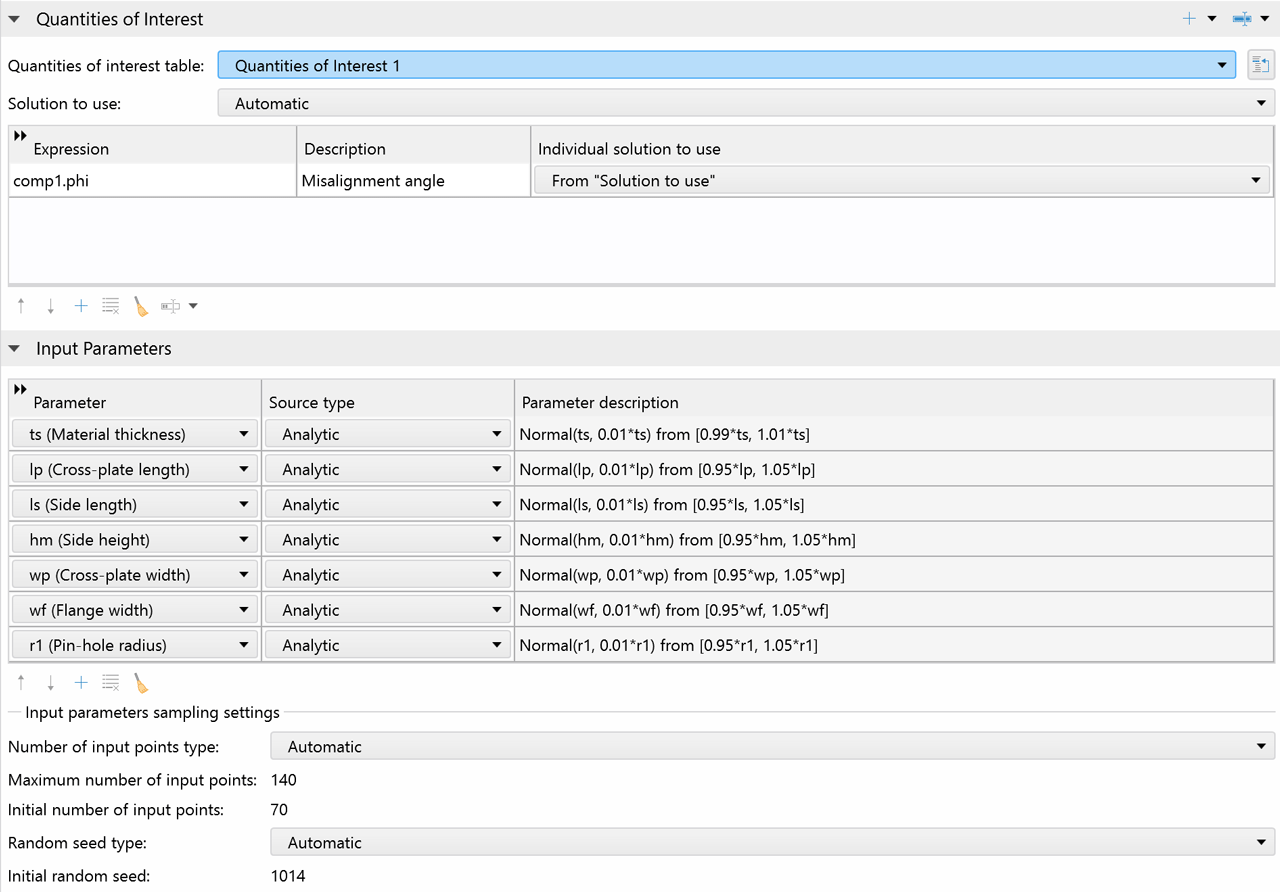
Une vue rapprochée des réglages des paramètres d'entrée et des quantités d'intérêt pour un modèle COMSOL Multiphysics.

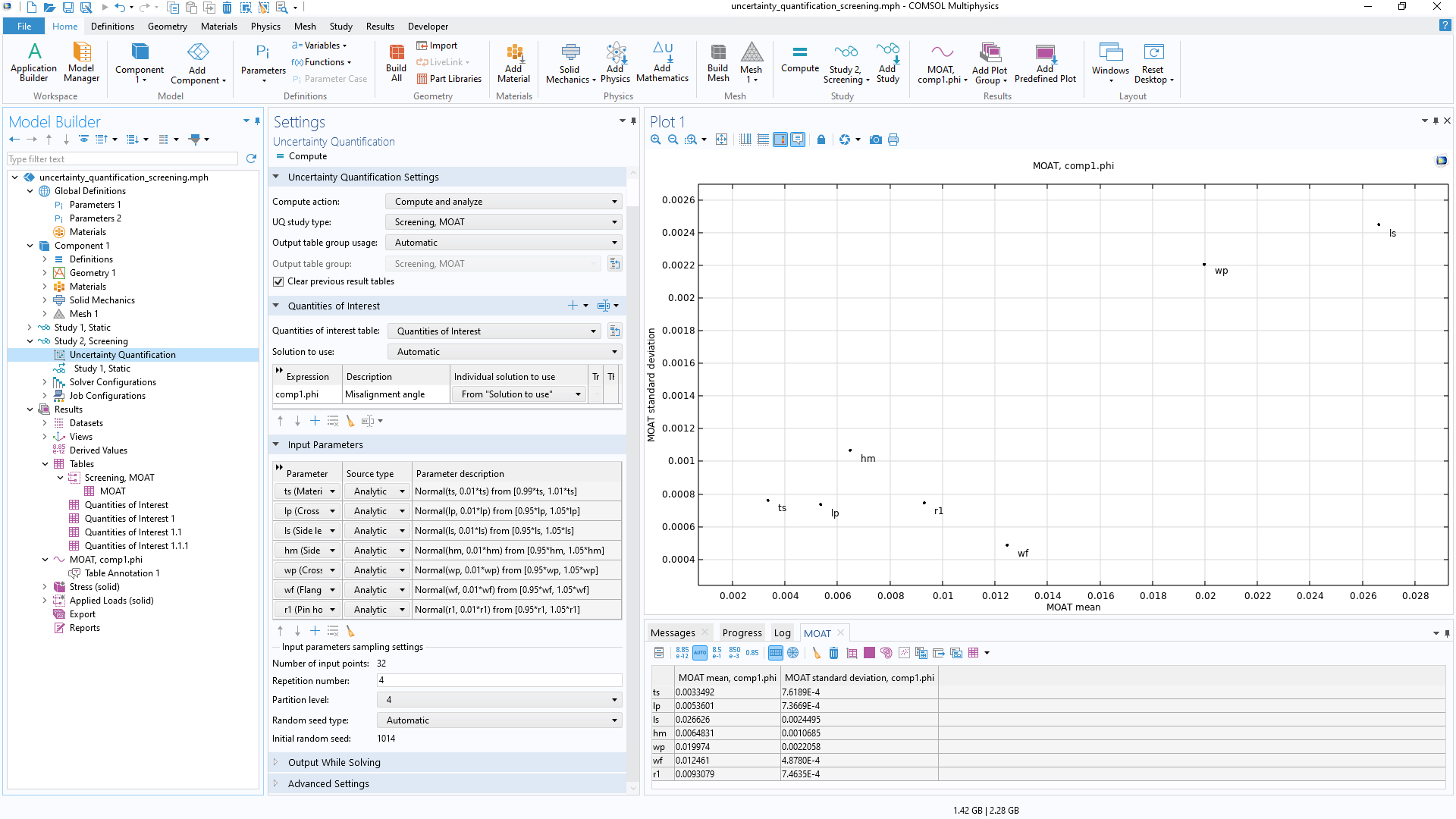
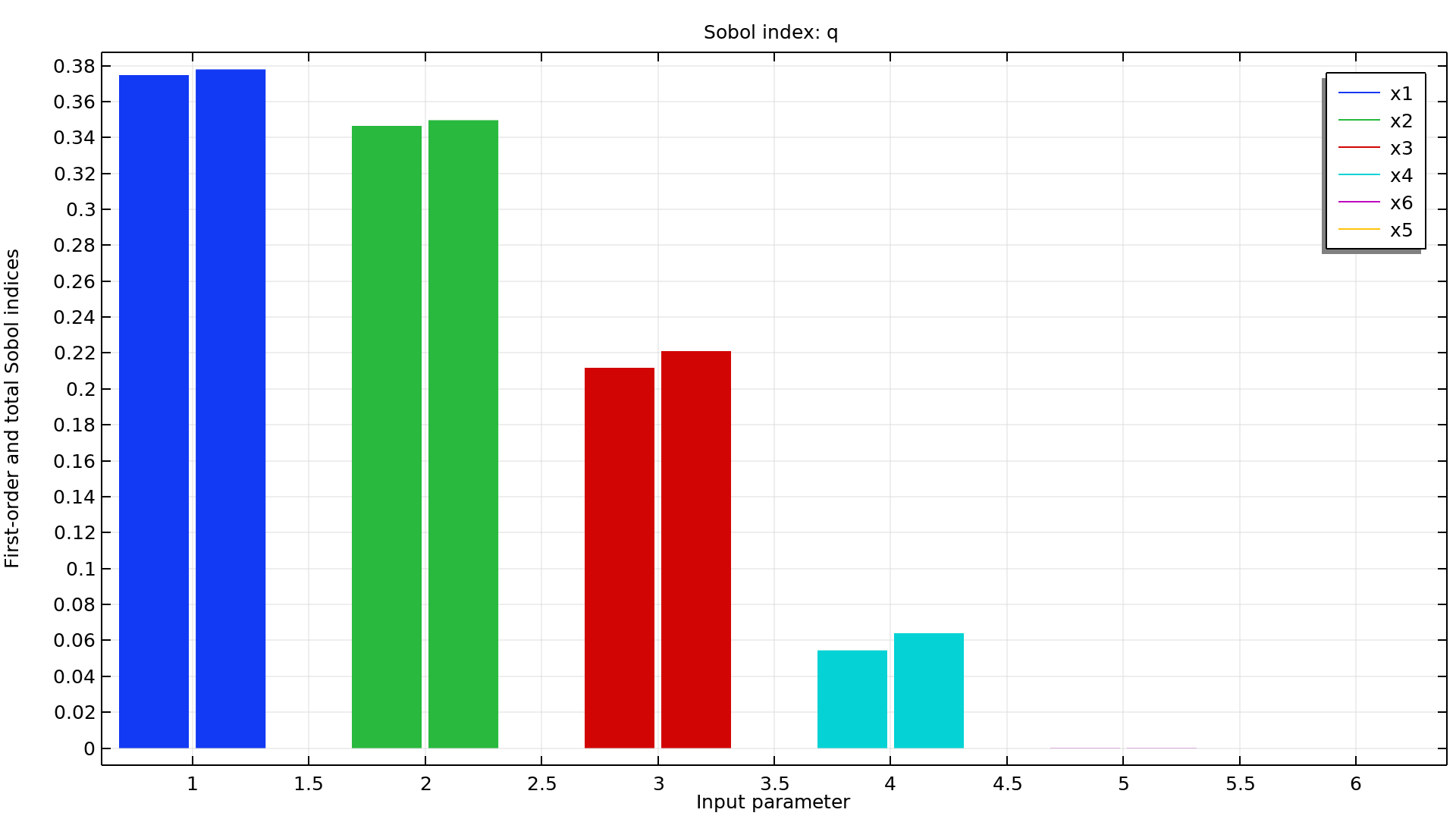
Paramètres d'entrée et quantités d'intérêt

Lors de l'exécution d'une étude de quantification des incertitudes, vous définissez un ensemble de quantités d'intérêt en fonction de la solution d'un modèle COMSOL Multiphysics®. De cette façon, les quantités d'intérêt sont des fonctions des paramètres d'entrée.

Dans le cas d'une analyse structurelle, les quantités d'intérêt peuvent être le déplacement maximal, la contrainte ou un angle de déviation. Pour une analyse de transfert de chaleur ou de CFD, les quantités d'intérêt sont par exemple représentées par la température maximale, la perte de chaleur totale ou le débit total de fluide. Dans le cas d'une simulation en électromagnétisme, elles peuvent être la résistance, la capacité ou l'inductance. Puisque le module Uncertainty Quantification est applicable à tout modèle physique calculé avec le logiciel COMSOL Multiphysics®, ainsi qu'à toute expression mathématique de diverses quantités des champs résolus, le choix de la quantité d'intérêt est illimité.

Toute entrée de modèle associé à une incertitude, qu'il s'agisse d'un paramètre physique, d'une dimension géométrique, d'une propriété matériau ou d'un paramètre de discrétisation, peut être traitée comme un paramètre d'entrée, et toute sortie de modèle peut être utilisée pour définir les quantités d'intérêt.

Les paramètres d'entrée peuvent être échantillonnés analytiquement avec des distributions de probabilité ou avec des données spécifiées par l'utilisateur. Les paramètres d'entrée échantillonnés analytiquement peuvent être corrélés et non corrélés, les paramètres d'entrée corrélés pouvant être regroupés en groupes de corrélation et échantillonnés à l'aide de la méthode de la copule gaussienne.

Screening

Le type d'étude Screening, MOAT met en œuvre une méthode de screening global légère en ressource qui donne une mesure qualitative de l'importance de chaque paramètre d'entrée. La méthode est purement basée sur un échantillon, utilisant la méthode MOAT (Morris one-at-a-time), et nécessite un nombre relativement faible d'évaluations du modèle COMSOL. Cela en fait une méthode idéale lorsque le nombre de paramètres d'entrée est trop important pour permettre des études de quantification des incertitudes plus coûteuses en termes de calcul.

Pour chaque quantité d'intérêt, cette méthode MOAT calcule la moyenne MOAT et l'écart type MOAT pour chaque paramètre d'entrée. Ces valeurs sont présentées dans un diagramme de dispersion MOAT. Le classement de la moyenne MOAT et des écarts types MOAT donne l'importance relative des paramètres d'entrée. Une valeur élevée de la moyenne MOAT implique que le paramètre influence de manière significative la quantité d'intérêt. Une valeur élevée de l'écart type MOAT implique en revanche que le paramètre est influent et qu'il interagit fortement avec d'autres paramètres, ou qu'il a une influence non linéaire, ou les deux.

L'interface utilisateur de COMSOL Multiphysics montrant le Constructeur de Modèles avec le noeud Quantification d'Incertitude en surbrillance, les réglages correspondants et un diagramme de dispersion MOAT dans la fenêtre graphique
Un graphique d'indice de Sobol pour une quantité d'intérêt, où x1 est représenté par des barres bleues, x2 par des barres vertes, x3 par des barres rouges et x4 par des barres sarcelles.

Analyse de sensibilité

Le type d'étude Analyse de sensibilité est utilisé pour calculer la sensibilité des quantités d'intérêt par rapport aux paramètres d'entrée. Ce type d'étude comprend deux méthodes: la méthode de Sobol et la méthode de corrélation.

La méthode de Sobol analyse la distribution complète des paramètres d'entrée et décompose la variance de chaque quantité d'intérêt en une somme de contributions provenant des paramètres d'entrée et de leurs interactions.

Pour chaque paramètre d'entrée, la méthode de Sobol calcule les indices de Sobol. L'indice de Sobol de premier ordre montre la variance d'une quantité d'intérêt attribuée à la variance individuelle de chaque paramètre d'entrée. L'indice de Sobol total montre la variance d'une quantité d'intérêt attribuée à la variance de chaque paramètre d'entrée et à son interaction avec les autres paramètres d'entrée. Les indices de Sobol pour chaque quantité d'intérêt et tous les paramètres sont présentés dans un graphique de Sobol dédié où les histogrammes sont classés par indice de Sobol total. La quantité d'intérêt est plus sensible au paramètre d'entrée ayant l'indice de Sobol total le plus élevé. La différence entre l'indice de Sobol total et l'indice de Sobol de premier ordre pour un paramètre d'entrée mesure l'effet de l'interaction entre cette entrée et les autres.

Par rapport à la méthode de screening, l'analyse de sensibilité est utilisée pour analyser quantitativement la manière dont les incertitudes des quantités d'intérêt se répartissent entre les différents paramètres d'entrée. Cette méthode nécessite davantage de ressources informatiques, car le calcul d'indices de Sobol précis repose sur un modèle de substitution de haute qualité.

La méthode de corrélation calcule la relation linéaire et monotone entre chaque paramètre d'entrée et les quantités d'intérêt. Pour l'analyse de sensibilité basée sur la méthode de corrélation, quatre types de corrélations sont calculés : corrélation bivariée, bivariée classée, partielle ou corrélation partielle classée.

Propagation des incertitudes

Le type d'étude Propagation des incertitudes est utilisé pour analyser comment les incertitudes des paramètres d'entrée se propagent à chaque quantité d'intérêt en estimant leur fonction de densité de probabilité (PDF). La physique sous-jacente qui fait correspondre les paramètres d'entrée aux quantités d'intérêt à travers les évaluations du modèle COMSOL Multiphysics® est, pour la plupart des applications, impossible à calculer analytiquement.

Pour cette raison, une analyse de Monte Carlo est nécessaire pour approximer les PDF. Comme pour la méthode de Sobol, un modèle de substitution est utilisé pour réduire considérablement le coût de calcul de l'analyse de Monte Carlo. Pour chaque quantité d'intérêt, une estimation de la densité du noyau (KDE) est effectuée et visualisée sous forme de graphe représentant une approximation de la PDF. En outre, sur la base de cette analyse, un tableau d'intervalles de confiance vous donne, pour chaque quantité d'intérêt, la moyenne, l'écart-type, le minimum, le maximum et les valeurs des limites inférieure et supérieure correspondant à des niveaux de confiance de 90%, 95% et 99%.

Un graphique linéaire d'estimation de densité de noyau avec KDE en axe des y et Predicted selon l'axe des x.
Un graphique 1D montrant deux quantités d'intérêt et une région ombragée où les paramètres d'entrée satisfont aux critères de fiabilité.

Analyse de fiabilité

Par rapport aux autres types d'études de quantification de l'incertitude, qui étudient l'incertitude globale associée à des quantités d'intérêt, la méthode d'Analyse de fiabilité, EGRA aborde une question plus directe: étant donnée un design nominal et certaines entrées spécifiques avec incertitudes, quelle est la probabilité que le design soit en échec? L'échec peut mener à une défaillance complète de la conception, mais il peut aussi être formulé en termes de critère de qualité.

Pour garantir la fiabilité, l'approche traditionnelle de la modélisation et de la simulation consiste à utiliser des marges de sécurité et les scénarios les plus défavorables. Avec une analyse de fiabilité appropriée, il est possible d'éviter la surestimation et la sous-estimation, car il est possible d'estimer une probabilité réelle. Une estimation approximative peut être tirée du tableau des intervalles de confiance de la propagation de l'incertitude pour chaque quantité d'intérêt. Mais avec l'analyse de fiabilité, vous pouvez définir un critère de fiabilité plus sophistiqué basé sur des combinaisons des quantités d'intérêt et des seuils correspondants. La méthode d'analyse de fiabilité globale efficace (EGRA) utilisée pour l'étude de fiabilité utilise de façon optimisée les ressources de calcul vers l'état limite qui différencie l'échec du succès d'une conception.

Modèles de substitution et surfaces de réponse

Les analyses de sensibilité calculées avec la méthode de Sobol, la propagation des incertitudes et l'analyse de fiabilité reposent toutes sur une analyse précise de type Monte Carlo. Celle-ci nécessite souvent un grand nombre d'évaluations pour obtenir une bonne précision. Pour les problèmes réalistes où une évaluation de modèle COMSOL Multiphysics® peut nécessiter des ressources de calcul très importantes et où l'analyse de quantification de l'incertitude implique un grand nombre de paramètres, une analyse Monte Carlo réalisée uniquement avec des évaluations du modèle COMSOL Multiphysics® est irréaliste d'un point de vue des ressources informatiques. Une caractéristique essentielle du module Uncertainty Quantification est sa capacité à former et à utiliser un modèle dit de substitution, également appelé méta-modèle, pour une analyse donnée de quantification des incertitudes dans le but d'économiser les ressources informatiques.

Un modèle de substitution est un modèle mathématique compact construit pour représenter et évaluer les quantités d'intérêt dans le domaine d'intérêt défini par les paramètres d'entrée. Ce modèle est complètement indépendant du modèle COMSOL Multiphysics® sous-jacent et peut, s'il est construit correctement, être utilisé à la place du modèle COMSOL Multiphysics® pour prédire les valeurs des quantités d'intérêt pour d'autres valeurs des paramètres d'entrée que celles résolues. Le procédé de construction d'un modèle de substitution est généralement adaptatif et le modèle de substitution peut se rapprocher du modèle original avec un haut degré de précision. Les tolérances définies par l'utilisateur vous permettent d'augmenter la précision des modèles de substitution. Un niveau de précision plus élevé nécessite des évaluations supplémentaires du modèle COMSOL Multiphysics®.

Une fois qu'un modèle de substitution a été construit, vous pouvez réaliser une vérification indépendante pour en tester sa validité, et vous calculez rapidement les données de la surface de réponse pour l'ensemble de l'espace des paramètres d'entrée. Une surface de réponse peut alors être visualisée, où une quantité d'intérêt est affichée en fonction de deux paramètres d'entrée à la fois.

Un graphique de surface de réponse dans la palette de couleurs arc-en-ciel.
Six graphiques affichés en séquence d'empilement, avec trois graphiques dans la palette de couleurs arc-en-ciel.

Quantification d'incertitude inverse

La quantification inverse des incertitudes (UQ inverse) est utilisée lorsque certains paramètres d'entrée possèdent une loi de probabilité inconnue, nommés paramètres de calibrage. Grâce la quantification inverse, des données expérimentales peuvent être rétro-propagées pour obtenir des informations sur les propriétés statistiques de ces paramètres. Pour exploiter l'UQ inverse, une loi de probabilité est préalablement requise pour chaque paramètre de calibrage avant de lancer l'analyse.

Des données expérimentales sont généralement disponible pour les quantités d'intérêt et les paramètres expérimentaux utilisés. Il y a également des paramètres de calibrage qui ne peuvent pas être directement mesurés. Considérons par exemple une expérience pour laquelle nous souhaitons calibrer le module d'Young d'un composant mécanique. Nous devrions réaliser une expérience mesurant la contrainte de traction en fonction du déplacement imposé au matériau. Une quantification inverse devrait alors être mise en oeuvre pour exploiter ces données expérimentales et la connaissance a priori du module d'Young pour calibrer la loi de probabilité qui reproduirait au mieux les valeurs mesurées de contrainte de traction. L'UQ inverse peut être appliquée à un large spectre de physiques, telle que la mécanique des structures, la mécanique des fluides, l'acoustique, le transfert thermique, l'électromagnétisme ou encore le génie chimique.

Pour que le calcul des lois de probabilité des paramètres de calibrage soit faisable, un modèle de substitution est utilisé en complément d'une méthode de Monte Carlo par chaîne de Markov. À l'issue du calcul, les lois de probabilité jointe et marginale des paramètres d'entrée calibrés peuvent être visualisées. En complément, une table listant les intervalles de confiance est générée, fournissant des informations telles que la moyenne, l'écart type, les valeurs maximale et minimale, les bornes supérieure et inférieure correspondant à un niveau de confiance de 90%, 95% et 99% pour chaque paramètre d'entrée calibré.

Chaque activité et chaque besoin en matière de simulation sont différents.

Afin d'évaluer pleinement si le logiciel COMSOL Multiphysics® répond ou non à vos exigences, nous vous invitons à nous contacter. En parlant à l'un de nos représentants, vous obtiendrez des recommandations personnalisées et des exemples détaillés qui vous aideront à tirer le meilleur parti de votre évaluation et vous guideront pour choisir les options de licence les plus adaptées à vos besoins.

Il vous suffit de cliquer sur le bouton "Contacter COMSOL", d'indiquer vos coordonnées et tout commentaire ou question spécifique, avant de soumettre votre demande. Vous recevrez une réponse d'un représentant de COMSOL très rapidement.

Prochaine étape:

Demander une démonstration du logiciel

Contacter COMSOL