Articles techniques et présentations

In general, macroscopic two-phase flow in porous media is a mixture of connected and disconnected oil flow. The latter is expressed as ganglion dynamics and drop traffic flow, patterns observed experimentally in pore network models [1,2] and real porous media [3,4]. This characteristic was adversely not taken into account in previous modeling approaches.

The mechanistic model DeProF [5], predicts the relative permeability of oil and water in terms of the capillary number, Ca, the oil/water flowrate ratio, r, the oil/water viscosity ratio, M, the advancing and receding contact angles, and a parameter vector, comprising the dimensionless geometrical and topological parameters affecting the flow. The DeProF model is the first mechanistic model describing the flow in terms of its actual independent variables, Ca, and r. It shows improved performance over the conventional modeling of saturation-described flow.

The computational effectiveness of the DeProF algorithm is based on an inherent hierarchical theoretical modeling approach: at pore scale, the different configurations of two-phase flow within unit cells [imbibition and drainage invoking larger non-wetting blobs (ganglia and large droplets) within pores, and core annular flow of tiny non-wetting droplets within pore throats] are modeled by implementing relatively simple computational schemes, i.e. lubrication approximation of Stokes flow and Young-Laplace law for the interfacial tension, to derive the corresponding unit cell conductances; then, the fractional distribution of conductances are scaled-up, using effective medium theory and mass & flowrate balances, into a macroscopic description of the flow.

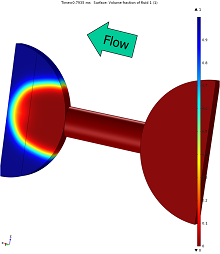
In the present work more realistic pore-scale flow calculations (CFD) in standard and more complex unit cells of the chamber-and-throat type and for various flow configurations (single phase, two-phase oil-water interfaces) have been performed. In the 2D pore network, "blister-and-flat-stick" unit-cell consisting of two short cylinders of class (j,k), linked together with a rectilinear cylindrical throat of elliptical cross section of class i were used. Similarly, in the 3D network, each elementary unit-cell is composed of two spherical parts (one-sixth each) of chambers of class j,k, interconnected with a straight cylinder of diameter class i. The precise geometry, the nominal dimensions of chambers and necks, and the occurrence frequency for each of the five classes (N=5) are described in [5]&[6].

Two-phase flow conductances (absolute permeabilities) of jik-class unit cells were estimated with sophisticated transient Level-Set multiphase FEM methods with moving mesh at the interfaces [7], and Lattice-Boltzmann two-phase flow with the BGK approximation [8] simulators. The following flow configurations have been considered: (i). Single-phase water and oil flow; (ii) Two-phase wetting/non-wetting (immiscible) flow with the interface contacting -at fixed angle- the pore conduit walls for cases: (ii.a) Receding interface across a jik unit-cell (gradual drainage) (ii.b) Advancing interface across a jik unit-cell (gradual imbibition).

Conductivities were calculated for predefined values of velocities or pressure gradients to deliver appropriate look-up tables (maps). The numerically calculated values of the simple pore conductivities have been compared with the conventional approaches (lubrication approximation) already used in the basic versions of the DeProF algorithm.