Articles techniques et présentations

Introduction

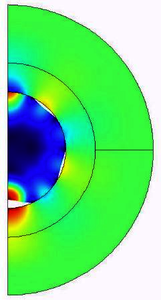
In this study, we investigate the damping mechanisms of particle resonances in acoustofluidic systems using the finite element framework of COMSOLTM. In the field of acoustic micro-manipulation, pressure waves are used for the contactless handling of micro-meter sized particles and cells. In recent years, new applications have made use of frequencies above 100 MHz. This is especially prominent in surface acoustic wave technology, where high frequency applications such as the one-cell-per-well technology emerged [1]. At frequencies above 100 MHz, the acoustic waves can excite resonances of soft micrometer sized particles such as polystyrene, which are often used in experiments. In order to predict the particle trajectories under these conditions, the acoustic radiation force needs to be computed. However, the amplitude of the resulting acoustic radiation force depends strongly on the damping mechanisms, especially the losses due to viscous damping and radiation. The radiation losses can be assessed using inviscid models in combination with non-reflecting boundary conditions, such as perfectly matched layers. Solving for the viscous losses leads to expensive computations, as the spatial discretization needs to account for the small viscous boundary layer. Hence, we investigate if introducing a damping coefficient φ similar to the work of Hahn et al. [2], allows to estimate the viscous losses without discretizing the viscous boundary layer.

Methods

To investigate the damping mechanisms of acoustically excited particle resonances and to assess our semi-analytical approximation, we use the finite element software package COMSOLTM to solve three problems: 1. Inviscid model: The fluid viscosity is neglected and all energy losses are due to radiation. This model is computationally cheap but not very accurate. 2. Viscous model: The viscosity of the fluid is accounted for and the thin viscous boundary layers are fully discretized in the model. The energy losses are due to combined radiation and viscous losses. This method is exact but computationally expensive. 3. Approximate model: The viscous damping is included in an acoustofluidic loss factor similar to Hahn et al. [2] and the estimated added mass is added to the particle density. This allows to incorporate the viscous losses in the calculation of the acoustic radiation force, without the need to resolve the viscous boundary layer. This model is computationally cheap and approximates the more exact viscous model.

Conclusion

So far, we found that the viscous boundary layer plays an important role and can generally not be neglected. First tests suggest that our simplified model performs reasonably well. We plan to investigate other damping mechanisms such as thermal and material damping. However, preliminary studies on two-dimensional models show that these additional effects can be neglected compared to the energy losses due to the viscous boundary layer and the radiation.

References [1] D. Collins, B. Morahan, J. Garcia Bustos, C. Doerig, M. Plebanski, and A. Neild. Nature Communications 6, 8686, (2015). [2] P. Hahn, and J. Dual. Physics of Fluids 27.6, 062005, (2015).