
Dans les systèmes microfluidiques, l’écoulement est toujours laminaire. C’est à la fois un avantage et un inconvénient — un avantage car l’écoulement est stationnaire, et un inconvénient car le mélange d’espèces se fait essentiellement par diffusion, ce qui peut prendre du temps. Un moyen simple de mélanger des espèces chimiques dans une puce microfluidique consiste à utiliser une microstructure de canaux en serpentin. En utilisant le logiciel COMSOL Multiphysics®, la périodicité de ce type de structure peut être exploitée pour déterminer la longueur de canal requise pour garantir que la solution sorte du système en étant bien mélangée.
Modéliser des systèmes microfluidiques périodiques avec COMSOL Multiphysics®
L’image ci-dessous montre un exemple de dispositif microfluidique composé de de canaux microfluidiques en serpentin. Des solutions diluées contenant des espèces chimiques peuvent entrer dans le système par les deux entrées. Les fluides se rejoignent et s’écoulent dans les canaux en serpentin. Le mélange des espèces chimiques se fait par diffusion, étant donné que l’écoulement dans les systèmes microfluidiques est laminaire. Pour mettre en place une simulation efficace, nous pouvons exploiter la périodicité de la structure et considérer une cellule unitaire qui se répète.
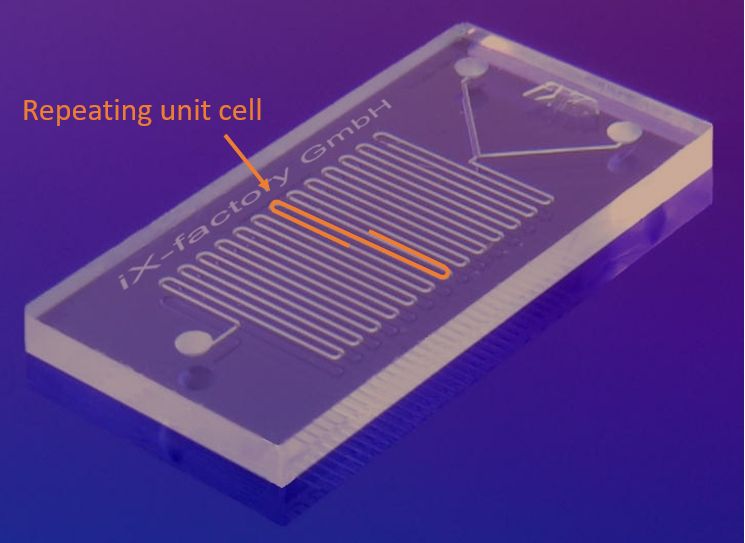
Un dispositif microfluidique typique. L’image a été modifiée. Image originale par IX-factory STK — Travail personnel, sous licence CC BY-SA 3.0, via Wikimedia Commons. L’oeuvre originale a été modifié.
Le canal en serpentin montré ici a déjà été abordé dans deux articles de blog précédents. Dans l’approche présentée dans le premier de ces articles de blog, “Using General Extrusion Operators to Model Periodic Structures”, l’écoulement laminaire est résolu pour une cellule unitaire répétée, ce qui réduit la charge du calcul. Le champ de vitesse est ensuite mappé sur la géométrie complète contenant plusieurs cellules unitaires répétées à l’aide d’un opérateur d’Extrusion générale. En s’appuyant sur le champ de vitesse ainsi mappé, le transport d’espèces diluées est résolu sur la géométrie complète, comme on peut le voir sur l’image suivante.

La première approche de modélisation pour simuler un dispositif microfluidique périodique. Le champ de vitesse est simulé sur une seule cellule unitaire puis mappé sur la géométrie complète. Le profil de concentration est résolu sur la géométrie complète.
Dans le second article de blog, “Exploiting Periodicity in Models with High Péclet Numbers”, le modèle est encore simplifié. L’article de blog met l’accent sur les systèmes microfluidiques ayant un nombre de Péclet élevé. Le transport d’espèces est dominé par l’advection plutôt que par la diffusion, et, par conséquent, la solution aval n’influence pas la solution amont. Il n’est donc pas nécessaire de résoudre le transport d’espèces sur le dispositif complet, comme cela est fait dans la première approche.
Pour des nombres de Péclet élevés, le transport d’espèces peut donc être calculé de façon séquentielle, une cellule unitaire après l’autre. Pour ce faire, le champ de vitesse est résolu sur une cellule unitaire, comme le montre l’image ci-dessous (“method 2”). Ensuite, le champ de concentration est résolu sur une cellule unitaire. En utilisant la fonctionnalité Extrusion générale, le champ de concentration de la sortie est mappé sur l’entrée. Pour s’assurer que la solution précédente est bien utilisée pour le mapping de la concentration à l’itération suivante, l’interface EDO et EAD sur frontière et la fonctionnalité Solution précédente sont utilisées.
Dans cet article de blog, nous présentons un moyen différent d’atteindre le même objectif: transférer les résultats de la sortie vers l’entrée pour le calcul séquentiel du transport d’espèces. Au lieu d’une EDO sur frontière, nous utilisons une variable d’état. La variable d’état est plus simple à implémenter que l’EDO, ce qui réduit la complexité du modèle.

Les deuxième et troisième approches de modélisation pour simuler un dispositif microfluidique périodique en utilisant seulement une cellule unitaire unique. Les méthodes diffèrent dans l’étape 3. Le mapping du profil de concentration de la sortie vers l’entrée d’une cellule unitaire peut être implémenté en utilisant soit une EDO, soit une variable d’état. (La dernière approche est décrite ci-dessous.)
Extrusion générale et variable d’état
La modélisation démarre avec la définition d’un opérateur d’Extrusion générale, genext1. L’opérateur se trouve dans Définitions > Couplages non locaux. L’opérateur est défini sur la frontière de sortie. Il mappe une expression — dans ce cas, la concentration — de la sortie vers l’entrée, grâce au déplacement spécifié en x.

L’opérateur Extrusion générale mappe une variable d’une frontière à une autre avec un décalage de 6 mm dans la direction x .
Dans la deuxième étape, la variable d’état est définie sur la frontière d’entrée. La fonctionnalité Variable d’état se trouve dans Définitions > Utilitaires de variables. Les variables d’état sont traitées comme des variables dépendantes dans le modèle. Contrairement aux variables dépendantes habituelles d’une interface physique, les variables d’état peuvent être mises à jour à l’initialisation de ou à l’issue de chaque étape paramétrique, ou à chaque pas de temps, ou seulement à l’initialisation. Les réglages pour cette variable d’état sont visibles dans la capture d’écran ci-dessous. La variable d’état est appelée c_b, et une fonction step est utilisée comme valeur initiale pour afficher le gradient de concentration initial à l’entrée. La fonction step est localisée en x = 0.5 mm, et la concentration initiale varie de 0 à 1 mol/m3 selon la localisation sur l’axe x. La variable d’état est toujours mise à jour au début de l’étape paramétrique. Cela signifie que la concentration en sortie issue de l’étape précédente est mappée sur l’entrée pour l’itération suivante.

La fenêtre de Réglages pour les variables d’état.
La variable d’état c_b est utilisée comme concentration à la frontière d’Ecoulement entrant dans l’interface Transport d’espèces diluées. Les données des variables d’état sont stockées aux points de Gauss, et non aux points nodaux. C’est la raison pour laquelle nous sélectionnons l’option Flux (Danckwerts) comme Type de condition limite, au lieu de Contrainte sur la concentration. La condition de concentration est appliquée aux points nodaux, tandis que la condition de Danckwerts impose un flux aux points de Gauss.

La variable d’état c_b est définie comme concentration à la frontière d’écoulement entrant.
Pour minimiser l’erreur d’extrapolation, la fonctionnalité Maillage identique est utilisée aux frontières d’entrée et de sortie.

La fenêtre de Réglages de la fonctionnalité Maillage identique. Les frontières 2 et 7 sont les frontières d’entrée et sortie, respectivement.
De la même façon que dans les articles de blog précédents, nous résolvons le modèle en deux étapes. Les paramètres de l’étape de l’étude sont visibles dans l’image ci-dessous. Dans la première étape d’étude, seule l’interface Ecoulement laminaire est résolue, sur une cellule unitaire. Le champ de l’écoulement est le même quel que soit le nombre de répétitions de la cellule unitaire que l’on considère. Ce qui n’est pas le cas pour le transport d’espèces. Dans la seconde étape, le Transport d’espèces diluées et la Variable d’état sont calculés. Nous introduisons en outre un paramètre n_unit_cells pour le calcul séquentiel des cellules unitaires répétées. Ce paramètre est utilisé dans un balayage de paramètres auxiliaires et évolue de 1 par incrément de 1 jusqu’à atteindre le nombre de cellules unitaires, 15 dans notre cas. A la fin de chaque calcul, la variable d’état est mise à jour et le champ de concentration au niveau de la sortie est mappé vers l’entrée pour la cellule unitaire suivante. Le paramètre Lancer la continuation pour est réglé sur Aucun paramètre et l’option Réutilisation de la solution de l’étape précédente sur Oui de façon à mettre à jour la variable d’état correctement.

Les réglages de l’étape d’étude, avec la fonctionnalité Balayage de paramètres auxiliaires activée. Le paramètre n_unit_cells reflète le nombre de cellules unitaires.
Nous obtenons ainsi le profil de concentration sur l’ensemble des répétitions de la cellule unitaire. Dans l’image suivante, les trois premières cellules unitaires sont visibles.
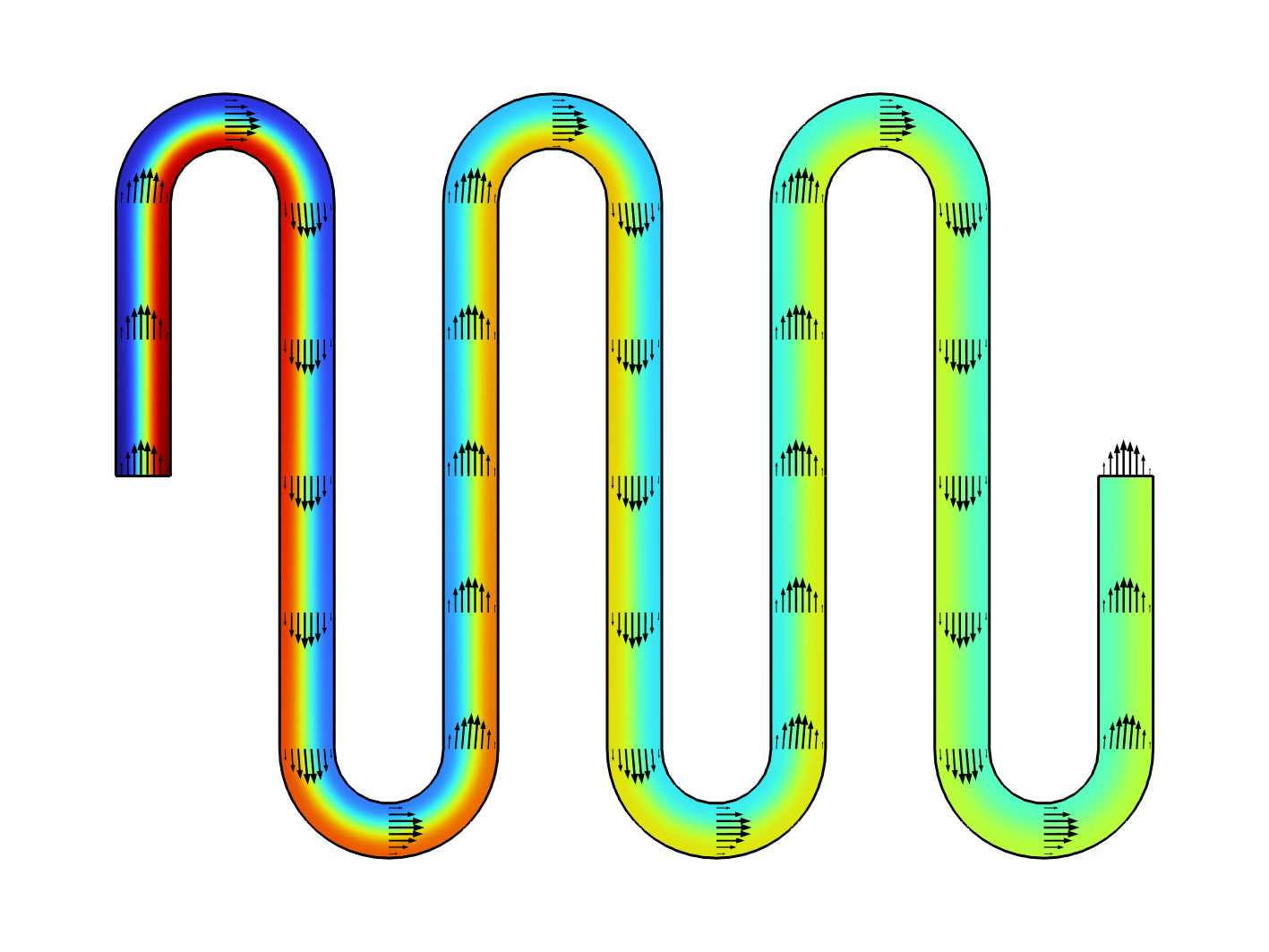
Profil de concentration des trois premières cellules unitaires.
Les résultats de simulation présentés ici peuvent être utilisés pour déterminer le degré de mélange et la longueur de canal nécessaire. Cette approche efficace, consistant à utiliser le balayage de paramètres auxiliaires, nous permet d’augmenter la taille du mélangeur à volonté. Pour mieux mesurer la qualité du mélange d’un système, nous pouvons nous appuyer sur l’indice de mélange (IM). L’indice de mélange est calculé à travers la section du canal et défini de la façon suivante:
où \textless{c}\textgreater représente la concentration moyenne sur la frontière de sortie et {\sigma} son écart-type.

L’indice de mélange en fonction du nombre de cellules unitaires.
Le graphique montre l’indice de mélange en sortie de chaque cellule unitaire pour 15 répétitions. Un indice de mélange de 0.98 est d’ores et déjà atteint après 5 cellules unitaires.
Point clés
La méthode montrée ici est très similaire à celle présentée dans notre article de blog “Exploiting Periodicity in Models with High Péclet Numbers”. Ces méthodes simplifient le modèle et économisent les ressources de calcul. La différence majeure avec la méthode précédente est l’utilisation d’une variable d’état plutôt que d’une EDO pour stocker et transférer la concentration de sortie à l’itération suivante. La méthode utilisant une variable d’état est plus facile à implémenter étant donné qu’elle ne requiert aucun changement dans la configuration solveur. De ce fait, nous recommandons l’utilisation de la méthode avec variable d’état pour modéliser des systèmes ayant un nombre de Péclet élevé. Cette approche peut également être employée pour des applications plus complexes telles que le mélange de plusieurs espèces chimiques qui réagissent pour former d’autres espèces.
En apprendre davantage
Vous souhaitez en savoir plus sur les fonctionnalités mentionnées ici? Consultez ces articles de blog:
- Découvrez en détail comment travailler avec les points de Gauss: “Introduction à l’intégration numérique et aux points de Gauss”
- Apprenez-en plus sur les Variables d’état: “How to Use State Variables in COMSOL Multiphysics®”
- Découvrez comment utiliser l’opérateur d’Extrusion générale: “Mapping Variables with General Extrusion Operators”
- Apprenez-en plus sur l’utilisation de l’opérateur d’Extrusion générale: “Examples of the General Extrusion Operator”



Commentaires (0)