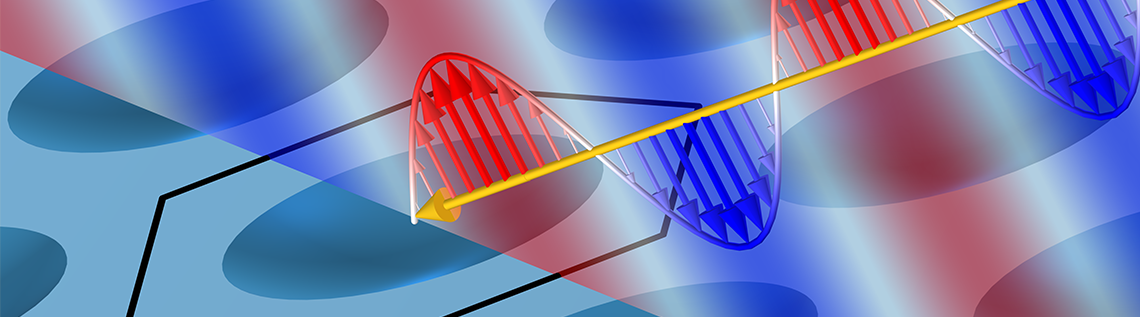
Lorsqu’une onde plane de rayonnement électromagnétique, par exemple la lumière, est incidente sur une structure périodique plane, il peut y avoir diffraction d’ordre supérieur. Cela signifie que la lumière sera non seulement réfléchie et réfractée selon la loi de Snell, mais aussi diffusée dans plusieurs directions distinctes, appelées ordres de diffraction. L’utilisation d’une approche géométrique peut nous aider à comprendre quand ces ordres sont présents et dans quelles directions la lumière se disperse. Découvrons-en davantage !
Comprendre la diffraction à partir de structures périodiques planes
Nous considérons ici une onde plane de lumière incidente sur une structure qui est infiniment périodique sur un plan. Les milieux situés au-dessus et au-dessous du plan peuvent avoir des indices de réfraction différents et sont supposés être exempts de pertes et d’une longueur infinie. Dans le plan de l’interface entre ces milieux, il peut y avoir des structures périodiques d’une complexité quelconque en termes de propriétés matériaux et de forme, à condition que ces formes se répètent périodiquement dans le plan. La lumière qui arrive sur une telle structure subit au moins une réflexion spéculaire ; la lumière peut également subir une réfraction (également appelée transmission spéculaire) et souvent aussi une certaine perte, l’énergie électromagnétique étant convertie en chaleur. Les angles de réflexion et de réfraction sont donnés par la loi de Snell, mais le calcul de la fraction de la lumière incidente qui est réfléchie, transmise ou dissipée dans la structure périodique nécessite une analyse numérique.
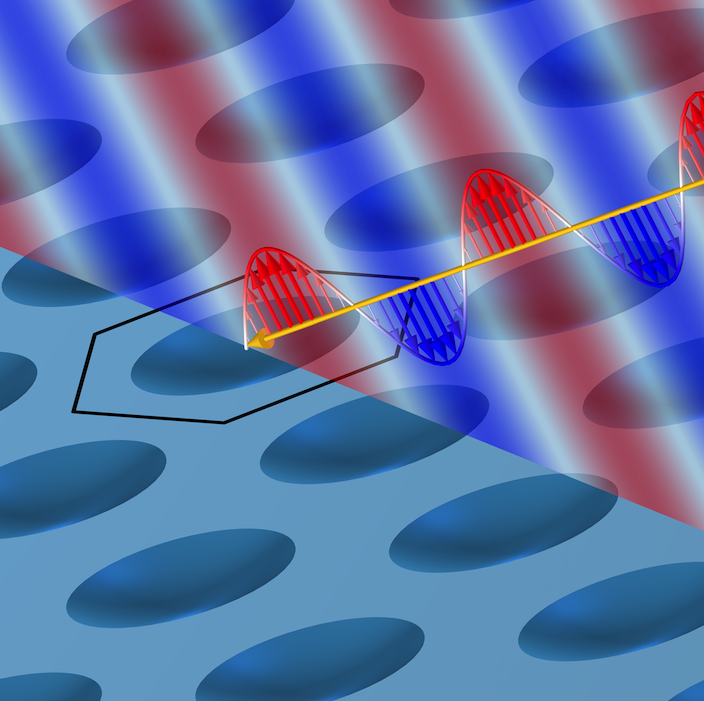
Onde plane incidente selon un certain angle sur une structure périodique plane. Une cellule élémentaire de la structure périodique est mise en évidence.
Comme nous l’avons mentionné, il existe également la possibilité d’une diffraction d’ordre supérieur. Cela se produit lorsque la lumière dispersée par la structure périodique interfère de manière constructive dans des directions distinctes. Un exemple de ce phénomène est illustré ci-dessous.
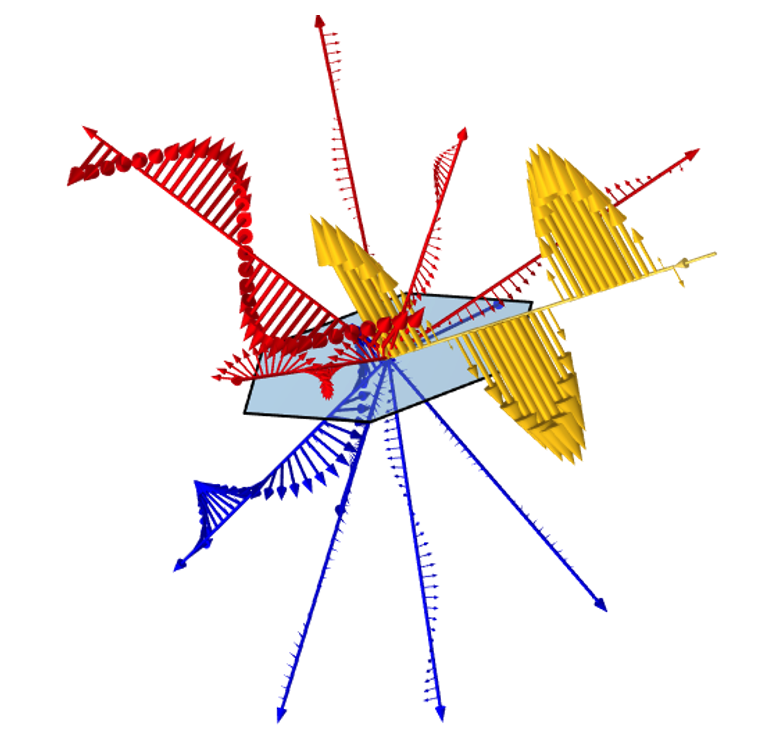
Illustration d’une onde plane à polarisation linéaire (jaune) incidente sur une cellule élémentaire périodique. La lumière incidente est diffusée en plusieurs ordres de diffraction différents avec des intensités et des polarisations différentes en réflexion (rouge) et en transmission (bleu).
Déterminer la fraction de lumière allant dans ces autres directions nécessite également la construction d’un modèle numérique, mais une approche purement géométrique, appelée construction d’une sphère d’Ewald, permet de comprendre les directions dans lesquelles la lumière se diffuse. Il est souhaitable de se familiariser avec cette approche avant de commencer l’analyse numérique, et c’est ce que nous allons faire ici. La construction géométrique de la sphère d’Ewald peut être utilisée à la fois pour les structures planes avec une périodicité selon une seule direction et pour celles avec une périodicité selon deux directions dans le plan.
Structures à périodicité unidirectionnelle
Certaines structures périodiques planes, telles que les grilles, présentent une variation périodique dans une seule direction, ce qui signifie qu’il n’y a pas de variation dans la structure selon la troisième dimension. Lorsque la lumière incidente se propage dans le plan normal à cette troisième dimension, la modélisation peut être réduite à un plan en deux dimensions, avec une périodicité le long d’une direction.
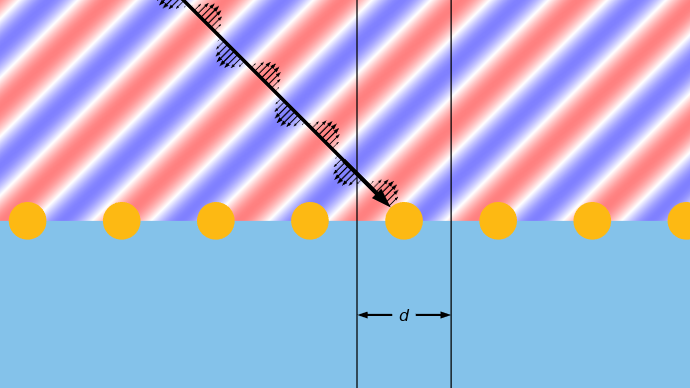
Onde plane incidente selon un certain angle sur une structure présentant une périodicité dans une seule direction, sans variation de la structure ou des champs le long de la direction hors plan. Une cellule élémentaire est mise en évidence.
Pour ces structures, il suffit de considérer l’espacement entre les cellules, d, et de commencer par dessiner un ensemble de points de trame dans l’espace réciproque, de sorte que les dimensions dans la figure suivante ont des unités de longueur inverse. La ligne de ces points de trame correspond au plan de l’interface de la structure périodique. L’espacement entre les points du réseau est 2\pi/d, et les points sont indexés à partir du point zéro du réseau, m=0, que l’on peut considérer comme situé au milieu de la cellule élémentaire. Ensuite, deux demi-cercles sont tracés au-dessus et au-dessous de la ligne des points du réseau. Ceux-ci ont un rayon de n_{r}2\pi/\lambda_{0} du côté de la réflexion et de n_{t}2\pi/\lambda_{0} du côté de la transmission, où n_{r} et n_{t} sont les indices de réfraction des deux côtés et \lambda_{0} la longueur d’onde de l’espace libre. Pour une lumière incidente arrivant avec un angle de \theta_{inc} par rapport à la normale, le centre commun de ces cercles est décalé du point zéro du réseau de sin(\theta_{inc})n_{r}2\pi/\lambda_{0}. Les points du réseau situés à l’intérieur de ces demi-cercles correspondent aux ordres de diffraction possibles.
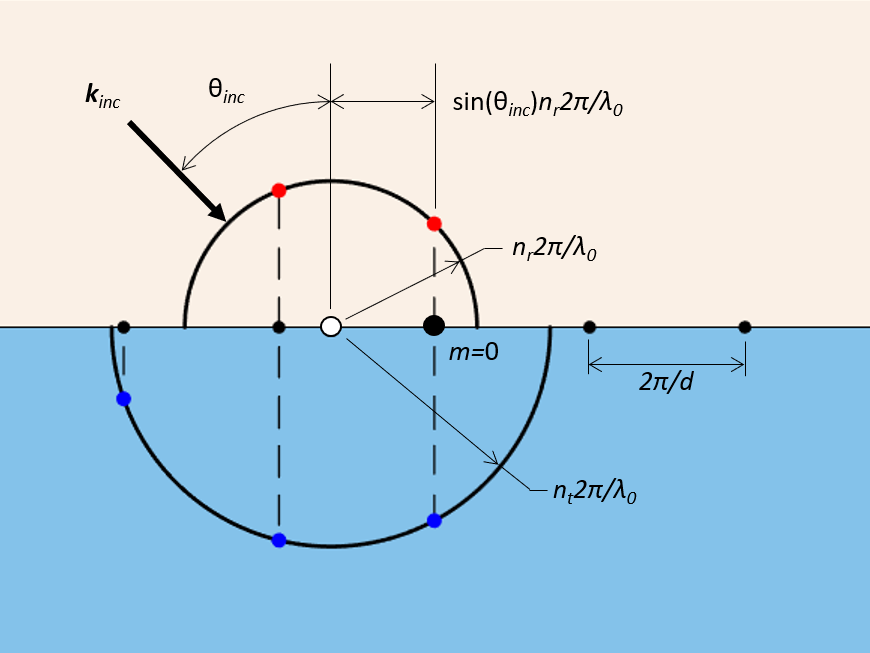
Construction géométrique utilisée pour déterminer les ordres de diffraction d’une structure plane avec périodicité dans une seule direction, éclairée par une onde plane incidente selon un certain angle. Notez que le centre des demi-cercles (point blanc) est décalé par rapport au point zéro du réseau.
Cette construction peut également être utilisée pour déterminer les directions dans lesquelles la diffraction se produira et attribuer un indice à chacune d’entre elles. Les vecteurs allant du centre des demi-cercles à la projection des points du réseau correspondent aux vecteurs \textbf{k} de chaque ordre de diffraction. L’indexation de ces points de réseau est de signe opposé des deux côtés. Les flèches pointant vers le point zéro du réseau seront toujours présentes ; elles représentent la réflexion et la transmission spéculaires. La présence d’autres ordres de diffraction dépend de la longueur d’onde, des indices de réfraction, de l’espacement et de l’angle d’incidence. Deux exemples de mise en place de ce type de modèle sont présentés dans la Bibliothèque d’Applications : Plasmonic Wire Grating (RF), qui fait appel au module RF, et Plasmonic Wire Grating (Wave Optics), qui fait appel au module Wave Optics.
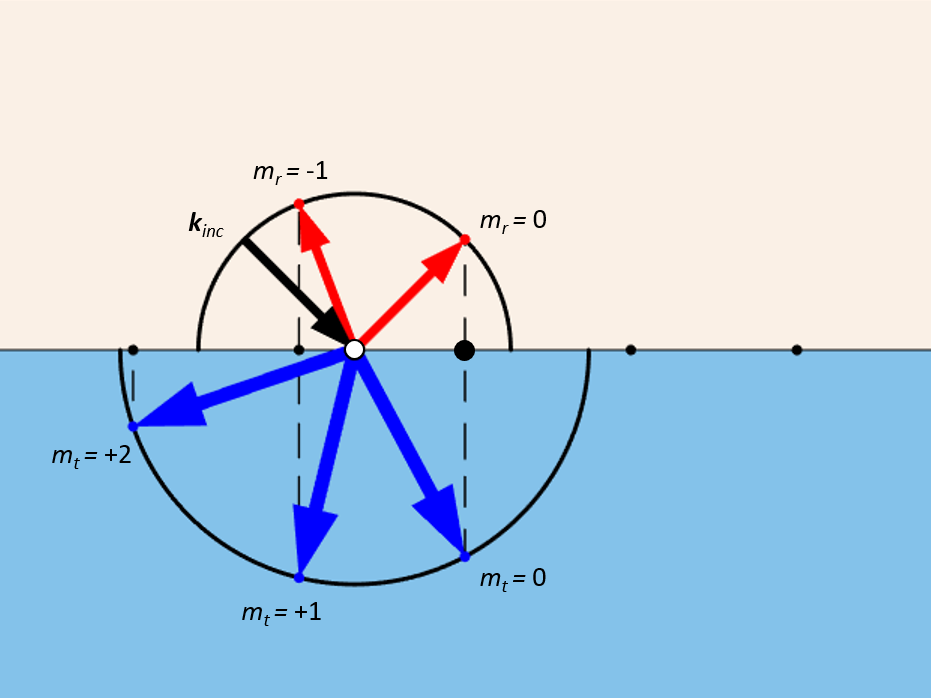
Vecteurs d’onde des différents ordres de diffraction d’une structure plane avec périodicité unidirectionnelle. Remarquez le changement de signe de l’indexation entre les ordres de diffraction par réflexion et par transmission.
Structures avec périodicité selon deux directions
Passons maintenant au cas de la diffraction par une structure plane présentant une périodicité selon deux directions dans le plan. La figure ci-dessous montre des cellules rectangulaires, rhomboïdales et hexagonales formant un plan. Celles-ci sont définies par deux vecteurs de cellule élémentaire, \textbf{a}_{1} et \textbf{a}_{2}, qui partent d’un point et suivent les arêtes adjacentes jusqu’au sommet suivant. Bien que nous soyons libres de travailler avec les coordonnées et l’orientation de notre choix, pour les besoins de ce billet de blog, nous choisirons de toujours aligner le vecteur \textbf{a}_{1} sur l’axe cartésien x global et de toujours regarder la cellule unitaire vers le bas, dans la direction de l’éclairage. Il existe également deux vecteurs de base, \textbf{b}_{1} et \textbf{b}_{2}, qui décrivent comment la cellule unitaire doit être déplacée dans le plan pour produire le motif de pavage. En d’autres termes, la création d’un motif sur l’ensemble du plan implique de copier la cellule unitaire par m\textbf{b}_{1}+n\textbf{b}_{2} pour toutes les valeurs entières de m et n. La norme du produit vectoriel de ces deux vecteurs est utilisée pour déterminer l’aire de la cellule élémentaire : A_{c} = ||\textbf{b}_{1}\times\textbf{b}_{2}||.

Les cellules élémentaires rectangulaires, rhomboïdales et hexagonales forment le plan 2D. Les vecteurs des cellules élémentaires correspondent à deux arêtes de la cellule, et les vecteurs de base décrivent comment les cellules doivent être déplacées pour structurer le plan.
Ces vecteurs de base sont utilisés pour définir deux vecteurs de diffraction dans l’espace réciproque : \textbf{d}_{1} = 2\pi(\textbf{b}_{2} \times \textbf{n})/A_{c} et \textbf{d}_{2} = 2\pi(\textbf{n} \times \textbf{b}_{1})/A_{c}, où \textbf{n} = (\textbf{b}_{1} \times \textbf{b}_{2})/A_{c} est le vecteur normal au plan de périodicité, l’axe +z. Ces vecteurs de diffraction sont perpendiculaires aux vecteurs de base et sont utilisés pour créer un réseau de diffraction dans le plan de périodicité en prenant des sommes entières : m\textbf{d}_1+n\textbf{d}_2, chaque point du réseau correspondant à une paire d’indices m et n dans les directions \textbf{d}_{1} et \textbf{d}_{2}. Du côté transmission de la cellule élémentaire, les points se trouvent aux mêmes endroits, mais les indices sont intervertis et de signe opposé.

Les vecteurs de diffraction et les points du réseau sont représentés dans l’espace réciproque.
Nous pouvons maintenant visualiser ces points de diffraction sur le plan de périodicité dans l’espace 3D et ajouter un hémisphère de rayon égal aux vecteurs d’onde dans le matériau au-dessus et au-dessous du plan. Ces hémisphères nous indiquent les ordres de diffraction présents en réflexion et en transmission. Nous centrons initialement cette sphère sur le point m = 0, n = 0, qui représente la lumière incidente dans la direction normale.
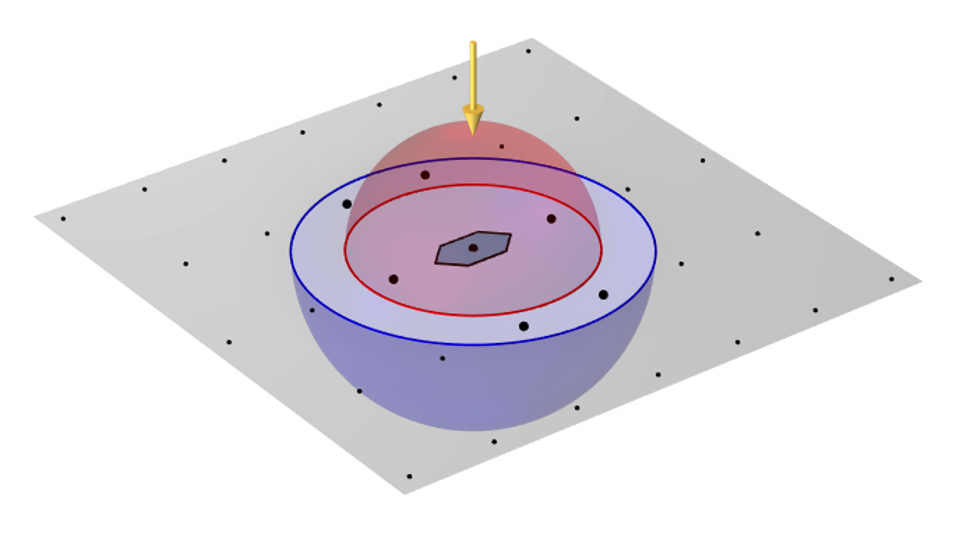
Onde de lumière plane (flèche jaune) arrivant dans la direction normale à une cellule élémentaire hexagonale périodique. Les points de diffraction sont tracés dans le plan de périodicité, et les points mis en évidence qui se trouvent dans les hémisphères de réflexion et de transmission indiquent les ordres de diffraction qui seront présents.
Examinons ensuite ce qui se passe lorsque l’angle d’élévation de l’incidence et l’angle d’incidence azimutale varient. En gardant à l’esprit que nous avons choisi la convention de maintenir le vecteur \textbf{a}_{1} aligné avec l’axe global +x, l’augmentation de l’angle d’élévation de l’incidence signifie que le vecteur de l’onde incidente est d’abord pivoté autour de l’axe –y ; ensuite, une augmentation de l’angle azimutal de l’incidence applique une rotation supplémentaire autour de l’axe +z. Ainsi l’angle d’élévation de l’incidence varie de 0^{\circ} \le \alpha_{1} < 90^{\circ}, et l’angle d’incidence azimutale varie de 0^{\circ} \le \alpha_{2} < 360^{\circ} , comme illustré ci-dessous. Le vecteur de l’onde incidente, ainsi que la normale au plan de périodicité, définissent le plan d’incidence. Le plan d’incidence est défini comme le plan xz dans le cas d’une incidence normale : \alpha_{1} = 0^{\circ}, \alpha_{2} = 0^{\circ}.

Les angles d’incidence en élévation et en azimut représentent un ensemble de rotations successives du vecteur de l’onde incidente (jaune), d’abord autour de l’axe –y, puis autour de l’axe +z. Le plan d’incidence est également représenté.
Ces modifications des angles d’incidence entraînent une modification de la position du centre des hémisphères. La distance dans l’espace réciproque entre le centre de l’hémisphère et le point m = 0, n = 0 est k_{r} = \text{sin(}\alpha_{1}\text{)}2π/ \lambda_r, et la position est décalée dans le plan de k_{x} = -k_{r}\text{cos(}\alpha_{2}\text{)} et k_{y} = -k_{r}\text{sin(}\alpha_{2}\text{)}, comme illustré ci-dessous. Ainsi, une modification de l’angle d’élévation et de l’angle azimutal entraîne souvent la présence d’un ensemble différent d’ordres de diffraction.
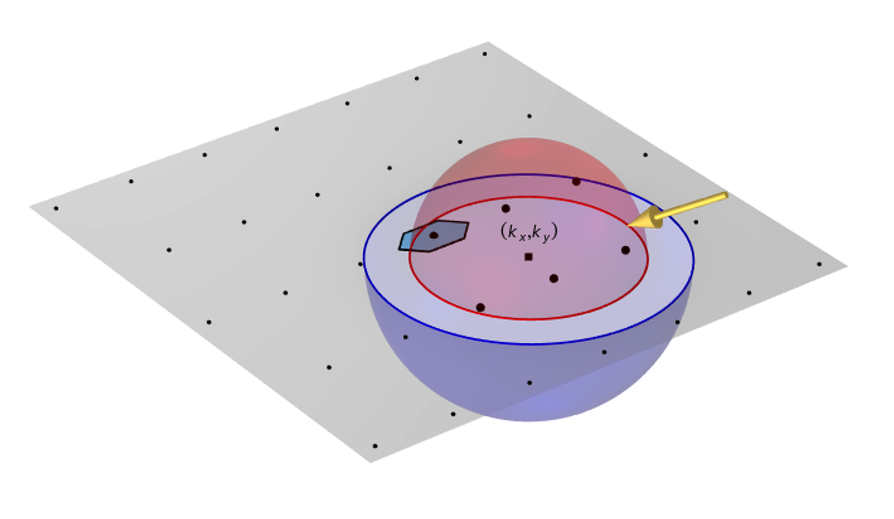
Une onde plane de lumière incidente présentant des angles d’élévation et d’incidence azimutal non nuls déplace le centre des hémisphères, de sorte qu’un ensemble différent d’ordres de diffraction est présent.
Ces hémisphères nous indiquent également les vecteurs d’onde de chaque ordre de diffraction. En projetant les points des ordres de diffraction sur les hémisphères, nous obtenons un autre ensemble de points, et les vecteurs d’onde de chaque ordre de diffraction sont égaux aux vecteurs allant du centre de l’hémisphère à ces points projetés.
La projection des points de diffraction sur les hémisphères donne le vecteur d’onde de chaque ordre de diffraction. Cette construction géométrique illustre les directions dans lesquelles la lumière incidente (jaune) sera diffractée après réflexion (rouge) et transmission (bleu). Vous pouvez interagir avec ce modèle 3D à l’aide de votre souris : clic gauche pour une rotation, clic droit pour le déplacement et molette de défilement pour le zoom.
Enfin, ces vecteurs nous informent également sur la façon dont l’état de polarisation sera indiqué. Pour chaque ordre de diffraction, un état de polarisation est indiqué en termes de composantes dans le plan et hors plan du vecteur de Jones. Le plan de chaque ordre de diffraction est le plan décrit par le vecteur d’onde et le vecteur normal au plan de périodicité. La composante hors plan du vecteur de Jones, pour tous les ordres de diffraction, correspond à une onde dont le champ électrique est parallèle au plan de périodicité.
Les directions des ordres de diffraction décrivent un ensemble de plans utilisés pour définir l’état de polarisation de chaque ordre de diffraction. Le plan d’incidence et un ordre de diffraction sont mis en évidence. Vous pouvez interagir avec ce modèle 3D à l’aide de votre souris : clic gauche pour une rotation, clic droit pour le déplacement et molette de défilement pour le zoom.
Conclusion
Nous arrivons à la conclusion de cet article concernant la construction géométrique de la sphère d’Ewald pour comprendre la diffraction par des structures périodiques planes. Cette sphère nous indique quels ordres de diffraction seront présents en réflexion et en transmission. Elle nous indique également leurs vecteurs d’onde et l’ensemble des plans utilisés pour définir l’orientation des vecteurs de Jones. Nous obtenons toutes ces informations automatiquement lorsque nous résolvons un modèle numérique. Il n’est donc pas nécessaire de passer par ce type de construction géométrique, mais cela peut être utile pour renforcer notre compréhension et notre intuition.
Pour aller plus loin
Si vous souhaitez vous lancer dans la modélisation de la diffraction d’ordre supérieur, les modèles suivants, qui peuvent être construits avec le module RF ou le module Wave Optics, constituent de bons points de départ.
- Modèles construits avec le module RF :
- Modèles construits avec le module Wave Optics :




Commentaires (0)