
Dans de nombreuses situations, il peut être intéressant de modéliser des signaux électriques périodiques, bien que non sinusoïdaux, afin de calculer les champs électriques, les pertes thermiques et les changements de température qui en résultent. Des trains d’impulsions électriques peuvent par exemple être appliqués à des tissus humains à des fins de neuromodulation, d’électroporation ou d’ablation thermique. Bien que ces signaux puissent être simulés par une approche temporelle, il est également possible de calculer efficacement la réponse linéaire à l’aide d’une transformée de Fourier. Regardons cela de plus près!
Table des matières
- Introduction
- Comprendre le contenu fréquentiel du signal d’entrée
- Résolution dans le domaine fréquentiel
- Reconstruction des résultats transitoires
- Utilisation des résultats de la FFT pour l’analyse thermique
- Modification du type d’impulsions et de leur espacement
- Ignorer les effets capacitifs pour simplifier davantage
- Conclusion
Introduction
Nous allons continuer à travailler avec le modèle utilisé comme exemple dans notre précédent article de blog, “Comprendre les différentes options d’excitation électromagnétique transitoire”, et le résoudre à l’aide de l’interface Courants électriques. (Cette interface est mise en évidence dans notre précédent article de blog et s’est avérée suffisante pour résoudre ce type de modèle). L’excitation du courant est une forme d’onde impulsionnelle trapézoïdale d’une période de 1 µs. La résolution est faite dans le domaine temporel. La tension du terminal et les pertes totales dans le modèle sont présentées ci-dessous.
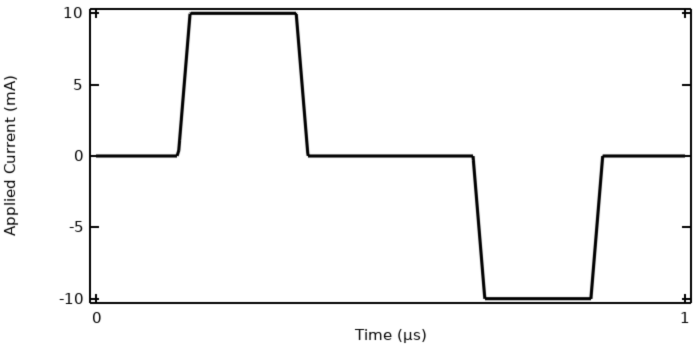
Le courant appliqué au modèle: une onde d’impulsion trapézoïdale.
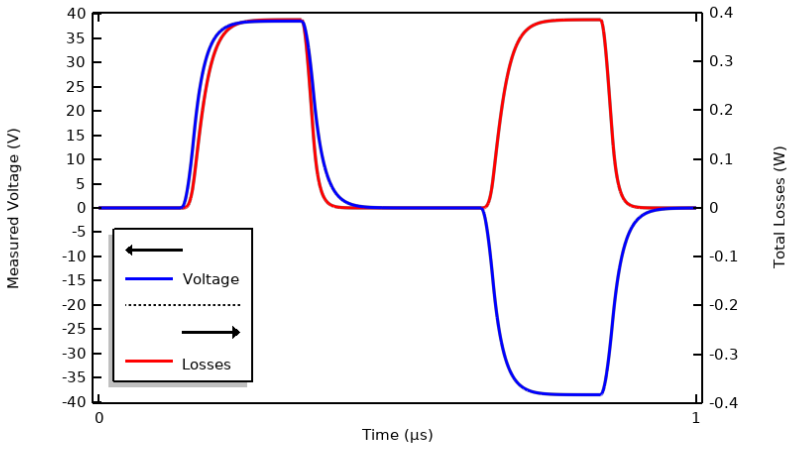
Calcul de la tension du terminal et des pertes au sein du matériau durant une période.
Nous pouvons également étendre le modèle pour résoudre la température et rendre la conductivité électrique dépendante de la température, obtenant ainsi un modèle multiphysique à couplage bidirectionnel. L’expression que nous utiliserons est \sigma (T) = 0.03\exp \left(-\frac{T-20^\circ \text{C}}{20\text{K}}\right) \text{S/m}.
Une condition limite de température fixe est appliquée sur les frontières latérales et sur la frontière inférieure du domaine de modélisation. Le modèle est résolu pour une seule période de temps (1 µs), ce qui permet d’examiner les variations de température au cours de cette période. Comme le montre l’image ci-dessous, le changement de température est minime.
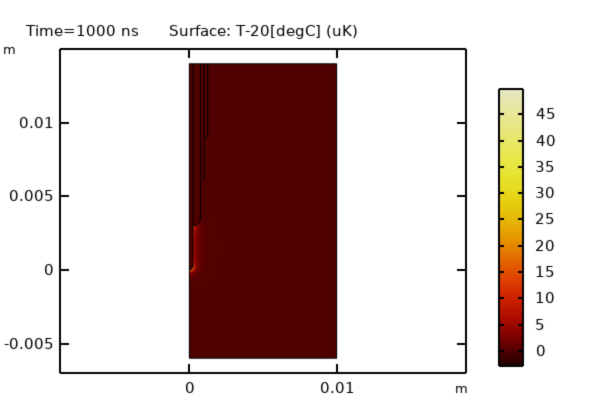
La variation de température calculée après 1 µs est faible.
Cependant, nous avons besoin de résoudre la variation de la température sur une durée beaucoup plus longue qu’une seule période, et dans ce cas, cette approche de modélisation devient trop coûteuse en termes de ressources de calcul. Nous devons donc envisager d’autres approches. Mais avant d’en arriver là, il y a plusieurs points à souligner à propos de ce modèle et de ses résultats :
- Le courant appliqué varie autour d’une valeur moyenne par cycle de zéro, de sorte que le signal d’entrée n’a pas de composante de courant continu (DC).
- La tension du terminal et les pertes calculées deviennent nulles entre deux impulsions.
- Ni la conductivité électrique ni la permittivité relative ne dépendent directement du champ électrique.
- La tension du terminal est en retard sur le courant, ce qui signifie que le système présente une capacitance importante.
- L’augmentation de la température au cours d’une période d’excitation est très faible.
Compte tenu de l’observation selon laquelle l’augmentation de la température est très faible sur une période similaire à la période d’excitation électrique, nous pouvons traiter le problème électrique comme étant localement linéaire dans le temps. Cela nous permet de reproduire les résultats en prenant la transformée de Fourier du signal appliqué, pour résoudre ensuite le modèle dans le domaine fréquentiel, avant d’utiliser une transformée de Fourier inverse pour reconstruire les résultats transitoires du modèle électrique. Cette méthode nous permet de savoir rapidement quelles harmoniques du signal d’entrée contribuent de manière significative à l’échauffement.
Pour résoudre la variation transitoire de la température sur une période beaucoup plus longue que la période d’excitation, il est possible d’utiliser un modèle à couplage bidirectionnel résolvant le champ de température en utilisant plusieurs interfaces Courants électriques, une pour chaque composante fréquentielle significative du signal d’entrée. Cette méthode sera beaucoup plus efficace en termes de ressources de calcul. Cette approche comporte plusieurs étapes, décrites dans les articles suivants de notre Centre d’apprentissage: “Understanding Periodic Signals and Their Frequency Content”, “Using the Inverse Fast Fourier Transform to Reconstruct a Transient Signal”, et “Setting Up and Solving Electromagnetic Heating Problems”. Nous les résumons ci-dessous.
Comprendre le contenu fréquentiel du signal d’entrée
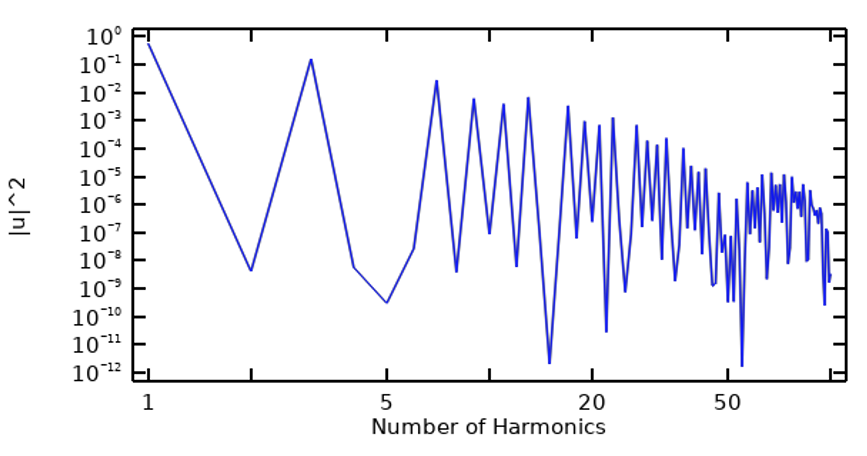
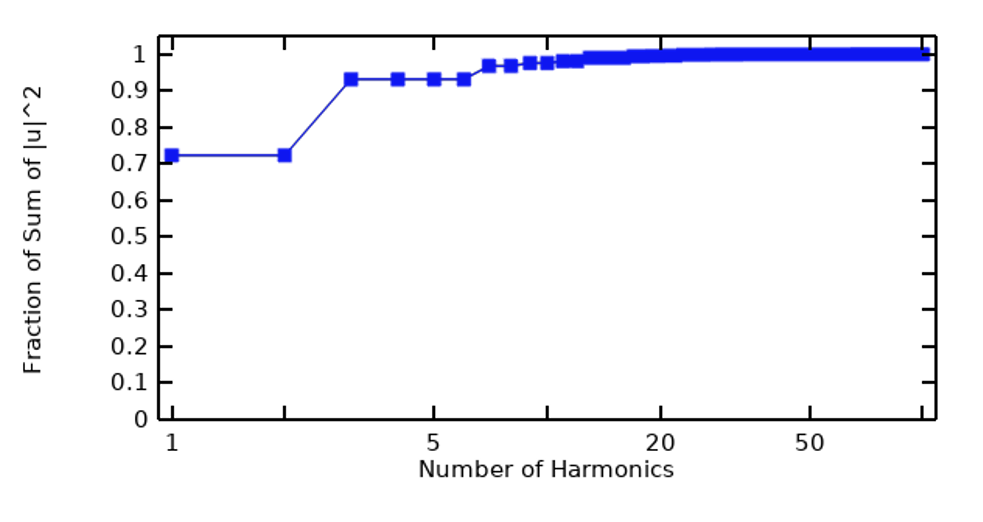
À partir d’un signal périodique, nous pouvons utiliser la Transformation de Fourier rapide (FFT) du signal pour analyser son contenu fréquentiel, ce qui peut être fait en termes d’amplitude de chaque harmonique, ainsi qu’en termes de somme cumulée jusqu’à l’harmonique en cours. Dans la figure ci-dessous, l’image de gauche montre le spectre en fréquence d’une onde d’impulsion trapézoïdale et l’image de droite présente sa somme cumulée.
Le contenu fréquentiel d’une onde d’impulsion trapézoïdale (à gauche) et sa somme cumulée (à droite).
On constate à l’issue de cette étape préliminaire, tout du moins pour cet exemple, que seul un nombre relativement faible d’harmoniques contribue à la majeure partie de l’énergie du signal, et que la contribution de certaines harmoniques est négligeable.
Résolution dans le domaine fréquentiel
En plus de la FFT du signal appliqué, nous devons également calculer la réponse du système à une excitation dans le domaine fréquentiel, avec une excitation de même amplitude pour toutes les fréquences. Notez que cela n’implique pas que la réponse du système sera équivalente à toutes les fréquences, sujet traité en profondeur dans notre article de blog “Understanding the Excitation Options for Modeling Electric Currents”. Les résultats obtenus en balayant une gamme de fréquences sont illustrés ci-dessous dans le graphique des pertes moyennées par cycle, dont nous pouvons déduire que l’impédance du modèle avec lequel nous travaillons varie de manière significative avec la fréquence. Dans ce cas, nous allons résoudre les 100 premières harmoniques, et une fois que nous saurons quelles sont les fréquences les plus importantes, nous pourrons utiliser un plus petit ensemble de fréquences.
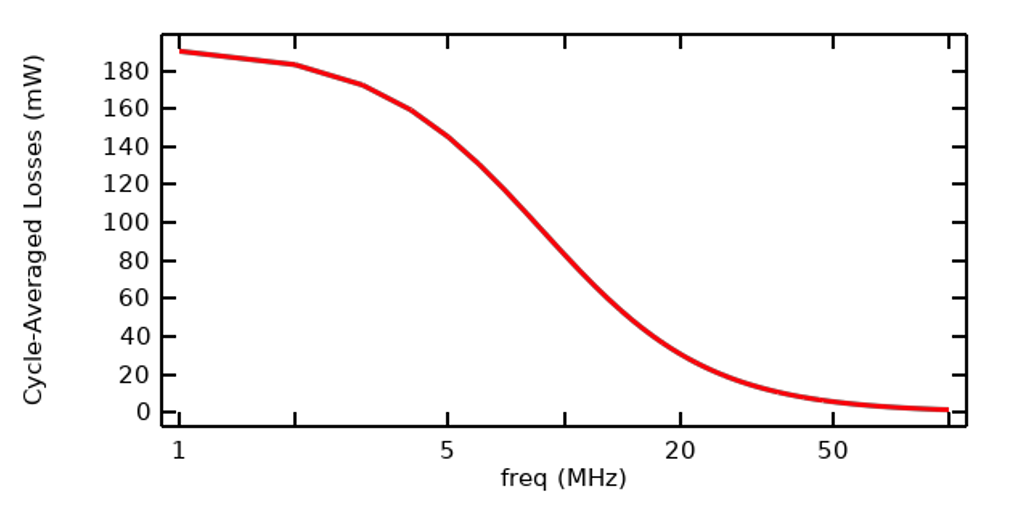
Graphique des pertes moyennes par cycle à l’intérieur de l’échantillon en fonction de la fréquence, pour une excitation identique sur toutes les fréquences.
Reconstruction des résultats transitoires
Comme nous disposons déjà de la FFT du signal d’entrée, une fois les résultats dans le domaine fréquentiel calculés pour une excitation unitaire sur toutes les fréquences considérées, nous pouvons utiliser la transformée de Fourier rapide inverse (IFFT) pour reconstruire la réponse transitoire du système. Le graphique ci-dessous montre une excellente corrélation, et l’approche IFFT requiert moins de ressources de calcul.
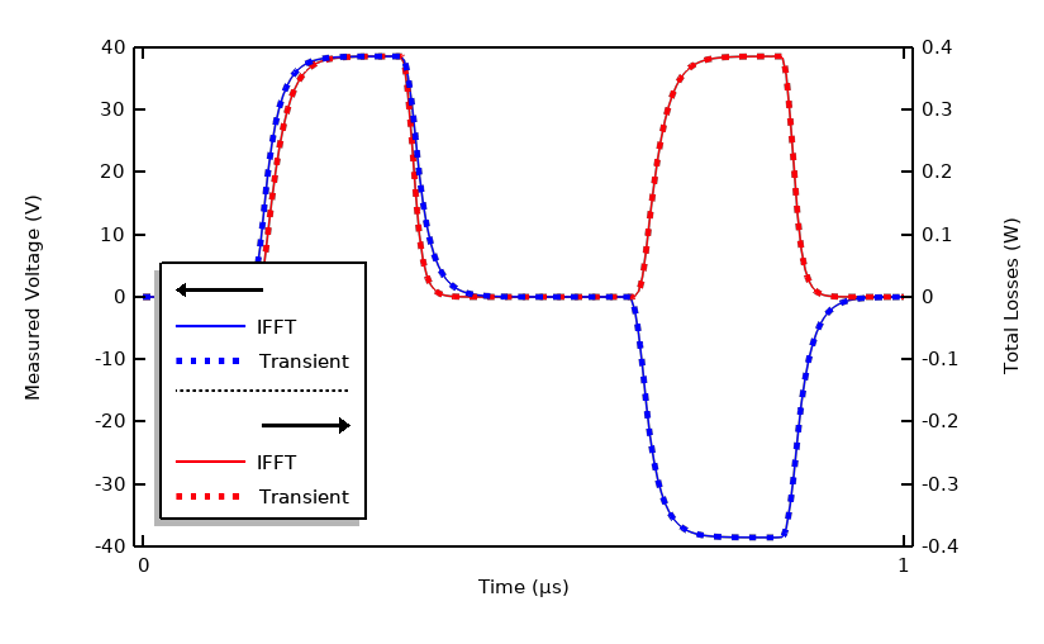
Comparaison des résultats transitoires et des résultats de la reconstruction par IFFT basée sur 100 harmoniques.
Cette excellente corrélation avec les résultats transitoires peut être utile mais bien souvent, nous nous intéressons uniquement à l’échauffement. Par conséquent, plutôt que d’évaluer les résultats de l’IFFT sur la base de corrélations avec l’approche temporelle, il est également utile de comparer les pertes intégrées sur la durée d’un cycle. Pour ce signal appliqué, 99 % des pertes sont obtenues en résolvant uniquement les première, troisième, septième et neuvième harmoniques. En d’autres termes, la valeur totale des pertes intégrées est très similaire, même si les résultats transitoires sont sensiblement différents.
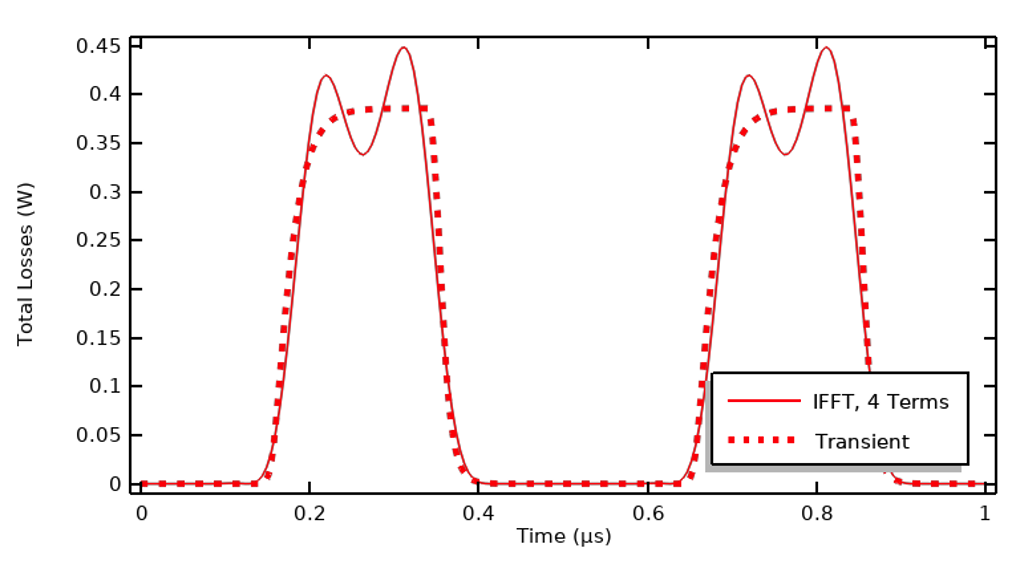
Comparaison des pertes calculées par l’approche temporelle et des pertes reconstruites par IFFT en utilisant seulement quatre harmoniques.
Comme on peut le voir sur le graphique ci-dessus, les courbes ne sont pas totalement corrélées. Malgré cela, l’intégrale des pertes sur une période concorde à 1 % près.
Utilisation des résultats de la FFT pour l’analyse thermique
Jusqu’à présent, nous avons reconstruit la variation des pertes transitoires sur une seule période, mais dans le cadre d’une analyse thermique, nous pourrions avoir besoin de modéliser des durées beaucoup plus longues, étant donné que les changements de température interviennent sur des durées beaucoup plus longues que la période des signaux électriques. Si nous travaillons avec des matériaux dont la conductivité électrique est fonction de la température, nous devrons inclure ce couplage bidirectionnel entre les physiques dans notre modèle. Si nous tentons de résoudre les champs électriques et de température en même temps, avec une résolution temporelle suffisamment fine pour capturer l’excitation électrique, nous obtenons un modèle particulièrement long à résoudre. Bien que cela soit parfois justifié, nous recherchons souvent une approche plus rapide, et c’est là que les données calculées précédemment deviennent très utiles.
Comme indiqué ci-dessous, les pertes transitoires peuvent être considérées comme uniformes dans le temps, en se basant sur la somme des contributions de quelques-unes des premières harmoniques. Ceci est valable dans l’hypothèse où les échelles de temps thermiques sont beaucoup plus longues que la période électrique.
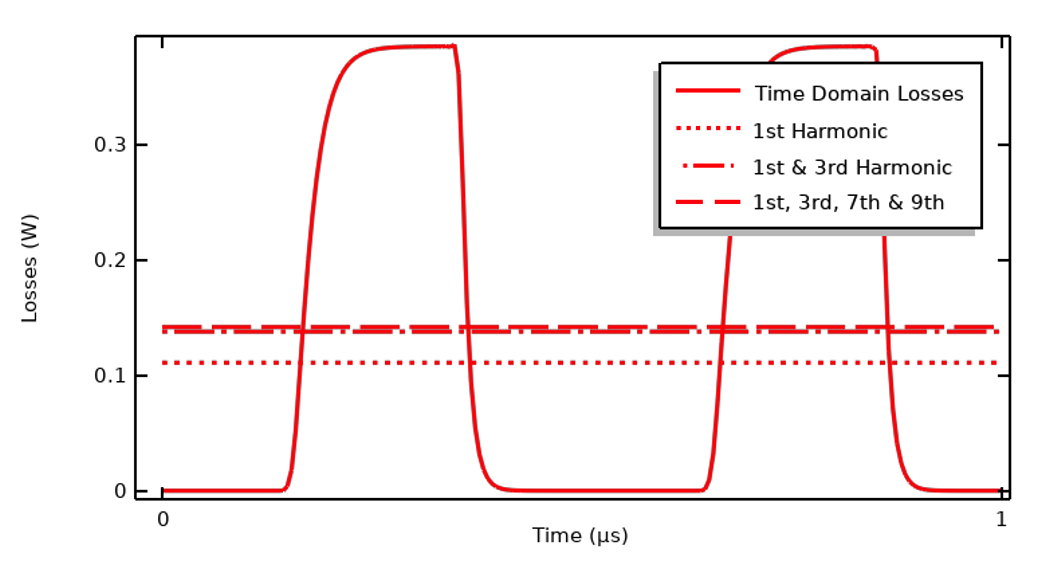
Graphique comparant les pertes transitoires avec la moyenne des pertes par cycle calculée sur plusieurs harmoniques.
Comme nous l’avons observé précédemment, pour ce signal d’entrée, nous n’avons besoin que de la fondamentale, de la troisième, de la septième et de la neuvième harmonique pour capturer 99 % de la chaleur sur une période. Cela signifie que nous pouvons mettre en place un nouveau modèle avec quatre interfaces physiques Courants électriques distinctes, chacune résolue dans le domaine fréquentiel pour une harmonique différente, et multiplier l’amplitude du courant appliqué pour chaque harmonique par le coefficient de Fourier correspondant du signal d’entrée. Ces interfaces peuvent ensuite être résolues avec un modèle thermique transitoire (ou stationnaire), qui calculera les variations de température et tiendra compte du couplage bidirectionnel induit par la dépendance à la température des propriétés électriques des matériaux. Cette approche est relativement plus efficace en termes de ressources de calcul et permet de modéliser une géométrie 3D. Pour savoir comment mettre en place de tels modèles où les résultats d’une FFT d’un signal d’entrée sont utilisés pour définir les chargements thermiques, consultez l’article suivant de notre Centre d’apprentissage: “Setting Up and Solving Electromagnetic Heating Problems”.

Augmentation de la température calculée dans un modèle 3D, résultant de l’échauffement moyen par cycle calculé à partir d’une somme d’harmoniques du courant périodique appliqué.
Modification du type d’impulsions et de leur espacement
Il convient également d’examiner ce qui se produirait si nous voulions modéliser un train d’impulsions, c’est-à-dire un signal strictement positif. Ce signal a une composante DC, ce qui rend théoriquement l’IFFT plus complexe puisque nous devons également prendre en compte la solution stationnaire. Mais comme nous ne nous intéressons ici qu’aux pertes thermiques, et si ces pertes s’annulent entre les impulsions, le signe de l’excitation n’a pas d’importance. En d’autres termes, l’échauffement électrique est le même quel que soit le sens du courant. Si l’échauffement au fil du temps devient nul entre les impulsions, il n’y a pas de composante DC de ce dernier à prendre en compte dans l’IFFT. Ainsi, même lorsqu’il s’agit d’un signal d’entrée strictement positif, il peut être judicieux de le traiter comme un signal passant du positif au négatif, uniquement dans le but de simplifier la reconstruction de l’IFFT. Le signal ci-dessous et le signal présenté précédemment sont identiques en termes de pertes calculées.
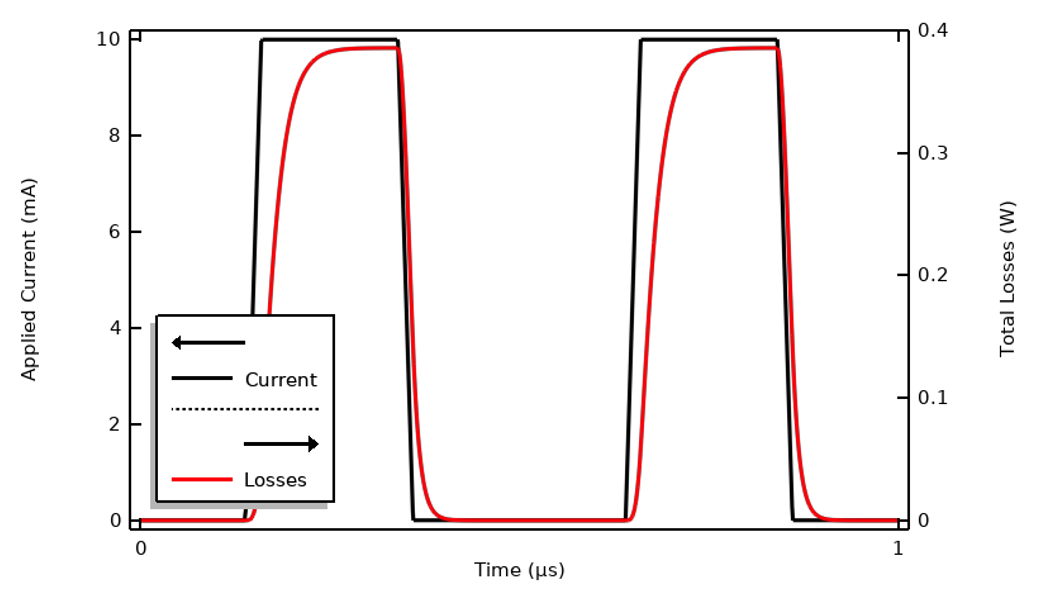
Un signal d’entrée strictement positif aura un échauffement identique à celui d’un signal symétrique, à condition que que le profil d’échauffement soit nul entre deux impulsions.
Nous pouvons également modifier l’espacement entre les impulsions. Cela augmente la période du signal d’entrée, de sorte que nous pourrions penser qu’il est nécessaire de refaire la FFT. Cependant, étant donné que l’échauffement s’annule entre les impulsions de notre signal original, le fait d’ajouter plus de temps pendant lequel l’échauffement est nul ne modifie pas les pertes dues à une seule impulsion. En d’autres termes, si nous avons un train d’impulsions avec une longue période de temps entre les impulsions, nous pouvons alors prendre la FFT d’un signal avec moins de temps entre les impulsions, car cela est suffisant pour prédire avec précision le profil d’échauffement et permet de réduire les coûts de calcul. Lors de la résolution du problème thermique couplé de manière bidirectionnelle, le signal appliqué doit être réduit d’un facteur égal à la racine carrée du rapport cyclique. Dans le graphique ci-dessous, les impulsions ont une durée équivalente mais la période est doublée, le rapport cyclique est donc de 0,5.
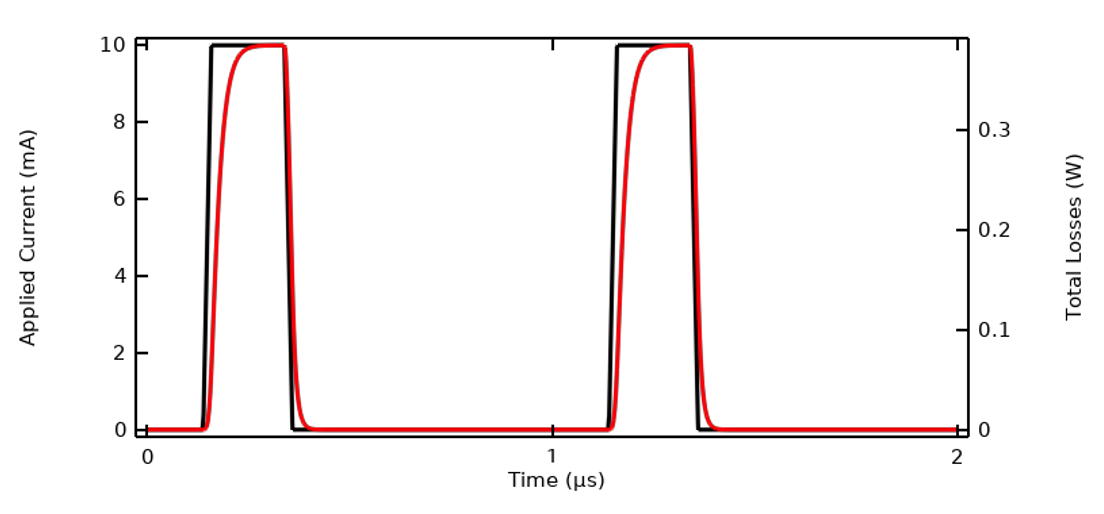
L’augmentation du temps entre les impulsions ne modifie pas le profil d’échauffement de chaque impulsion.
Ignorer les effets capacitifs pour simplifier davantage
L’exemple que nous avons examiné jusqu’à présent a été conçu (en termes de propriétés matériaux et de forme d’onde) pour illustrer un cas où l’approche FFT est la plus utile. Ce niveau de complexité n’est pas toujours nécessaire. Revenons à notre premier graphique du courant appliqué et de la tension au terminal et recréons-le avec un matériau différent, dont la conductivité électrique est dix fois supérieure. Nous obtiendrons une réponse comparable au graphique ci-dessous. Le décalage entre la tension et le courant est négligeable par rapport à la période, ce qui signifie qu’il n’y a pratiquement pas d’effets capacitifs. En d’autres termes, l’impédance du système est quasiment purement résistive et constante sur la plage de fréquences qui nous intéresse. De même, si le même signal était utilisé mais qu’il était dix fois plus lent, la réponse serait similaire.
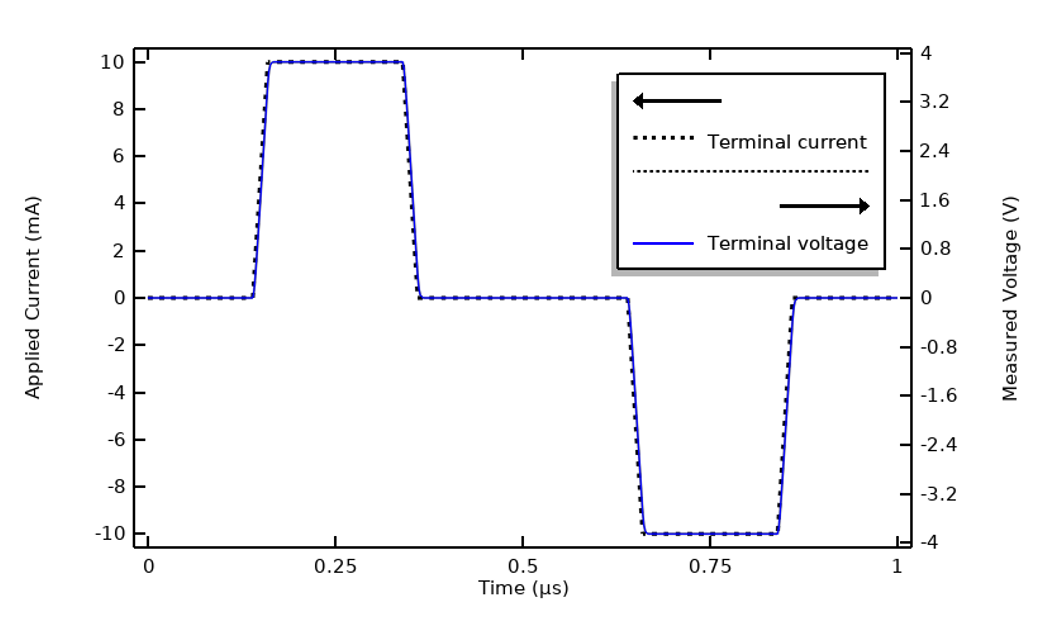
Une conductivité électrique dix fois plus grande modifie la réponse du système. Les effets capacitifs sont désormais négligeables.
En supposant que nous avons affaire à un système quasiment purement résistif et que la conductivité électrique est constante par rapport à la fréquence du signal appliqué, il est possible de simplifier le modèle électrique en le ramenant à un problème de courant continu stationnaire et donc d’ignorer totalement les effets capacitifs et les courants de déplacement qui en résultent. L’interface physique Courants électriques peut alors être résolue en Stationnaire, et le signal DC appliqué est la racine carrée de la moyenne par cycle du carré du signal transitoire :
Cette expression est la même que l’excitation se fasse par le biais d’un courant, d’une tension ou d’une tension terminée. Cette simplification est valable tant que les propriétés électriques sont constantes par rapport à la fréquence et à l’intensité du champ électrique.
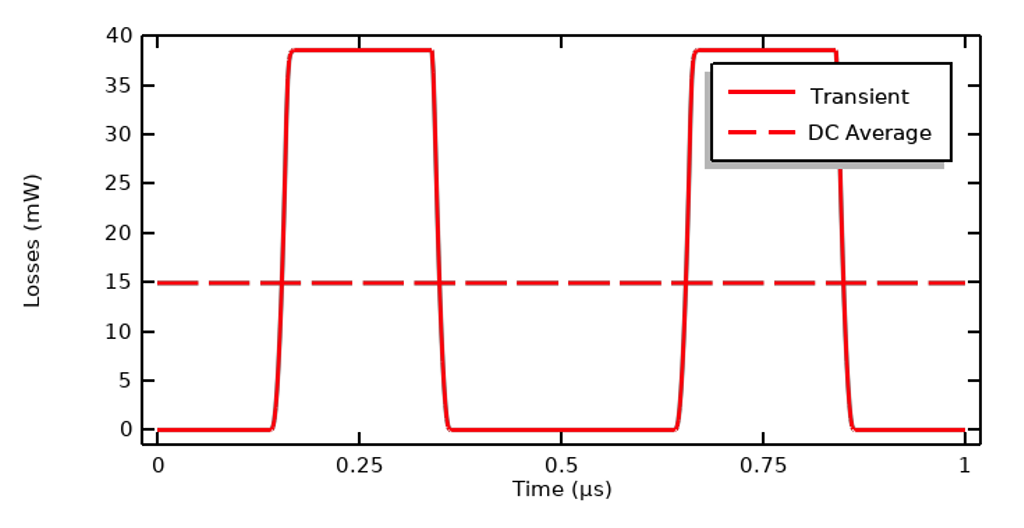
Les pertes transitoires pour un matériau quasiment purement résistif et la moyenne équivalente en courant continu.
Conclusion
Nous avons vu comment modéliser une excitation électrique périodique et comment elle peut souvent être réduite à une seule période. En effectuant la FFT du signal d’entrée, il est possible d’identifier le contenu fréquentiel significatif. Ainsi, la réponse transitoire du système peut être prédite en combinant la résolution d’un ensemble de fréquences avec une étape IFFT.
Les résultats de cette FFT et de cette IFFT peuvent servir à prédire la réponse temporelle et être utilisés comme données d’entrée dans une simulation de chauffage électrothermique. Il peut être particulièrement avantageux d’approximer un signal périodique comme une somme de plusieurs harmoniques, permettant de traiter cela de manière très efficace, comme un problème multiphysique à couplage bidirectionnel. Pour certains types de problèmes, nous pouvons encore simplifier en ignorant complètement le contenu fréquentiel.
Si vous travaillez dans ce domaine, il est important d’avoir conscience de toutes ces complexités et simplifications lorsque vous construisez vos modèles multiphysiques.



Commentaires (0)