
Il est probable que vous rencontriez le concept d’intégration numérique et de points de Gauss dans vos modèles éléments finis, et ce dans différents contextes. Dans ce billet de blog, nous expliquons dans quels cas et pour quelles raisons l’intégration numérique est utilisée. Les options disponibles dans le logiciel COMSOL Multiphysics® pour examiner et modifier les schémas d’intégration numérique sont également mises en évidence. Enfin, nous abordons la question de l’utilisation de degrés de liberté associés aux points de Gauss.
Table des matières
- Qu’est-ce que l’intégration numérique ?
- Intégration des contributions faibles
- Modifier l’ordre d’intégration
- Intégration réduite
- Opérateurs d’intégration
- Intégration durant l’exploitation des résultats
- Fonctions de forme des points de Gauss
- L’opérateur gpeval
Qu’est-ce que l’intégration numérique ?
Pour calculer l’intégrale de fonctions non triviales sur des domaines quelconques, il est nécessaire de faire appel à des méthodes d’intégration numérique, également appelées méthodes de quadrature. L’idée est de remplacer l’intégrale par une somme, dans laquelle l’intégrande est échantillonnée sur un ensemble discret de points. Cette méthode peut être formulée de la manière suivante
Où xi et wi désignent respectivement la position du point d’intégration et le facteur de pondération correspondant. Les points d’intégration sont souvent appelés points de Gauss, même si, en toute rigueur, cette dénomination n’est correcte que pour les points d’intégration définis par la méthode de quadrature de Gauss. Dans COMSOL Multiphysics®, la véritable quadrature de Gauss est utilisée pour l’intégration en 1D, en 2D pour les éléments quadrilatéraux et en 3D pour les éléments hexaédriques. D’autres schémas similaires sont employés pour les autres types d’éléments.
Méthode de quadrature de Gauss
Dans la méthode de quadrature de Gauss, la position des points d’intégration et leurs pondérations sont choisies de manière à ce qu’un polynôme de degré aussi élevé que possible puisse être intégré de manière exacte. Étant donné qu’un polynôme de degré N contient N+1 coefficients et qu’une règle de quadrature de Gauss à M points contient 2M paramètres (position et pondération), l’ordre le plus élevé du polynôme qui peut être intégré de façon exacte est N = 2M – 1.
La quadrature de Gauss permet d’intégrer efficacement les champs pouvant être bien approximés par un polynôme d’un certain degré. Les points d’intégration et les pondérations pour les premiers ordres de la quadrature de Gauss en 1D sont indiqués dans le tableau ci-dessous. L’intégrale est définie sur l’intervalle normalisé [-1,1].
| Ordre (M) | Précision (N) | Position (xi) | Pondération (wi) |
|---|---|---|---|
| 1 | 1 | 0 | 2 |
| 2 | 3 | ±0.577 | 1 |
| 3 | 5 | 0, ±0.775 | 0.889 (= 8/9), 0.556 (= 5/9) |
| 4 | 7 | ±0.340, ±0.861 | 0.652, 0.348 |
| 5 | 9 | 0, ±0.538, ±0.906 | 0.569, 0.479, 0.237 |
Dans COMSOL Multiphysics®, les ordres d’intégration sont désignés par le degré du polynôme pouvant être intégré de façon exacte. Seuls les nombres pairs sont utilisables. Pour une véritable intégration au point de Gauss, la précision est, comme indiqué ci-dessus, toujours une puissance impaire. L’ordre d’intégration désigné par le logiciel comme étant “4” aura en fait une précision de 5 sur les formes d’éléments pour lesquelles la quadrature de Gauss est utilisée.
Exemples de quadrature de Gauss
Pour illustrer la méthode de quadrature de Gauss, considérons la fonction
Sur le carré défini par -1 ≤ x ≤ 1, -1 ≤ y ≤ 1, l’intégrale de cette fonction est 1. Comme on peut le voir sur le graphique ci-dessous, cette fonction présente une distribution relativement complexe sur le domaine.
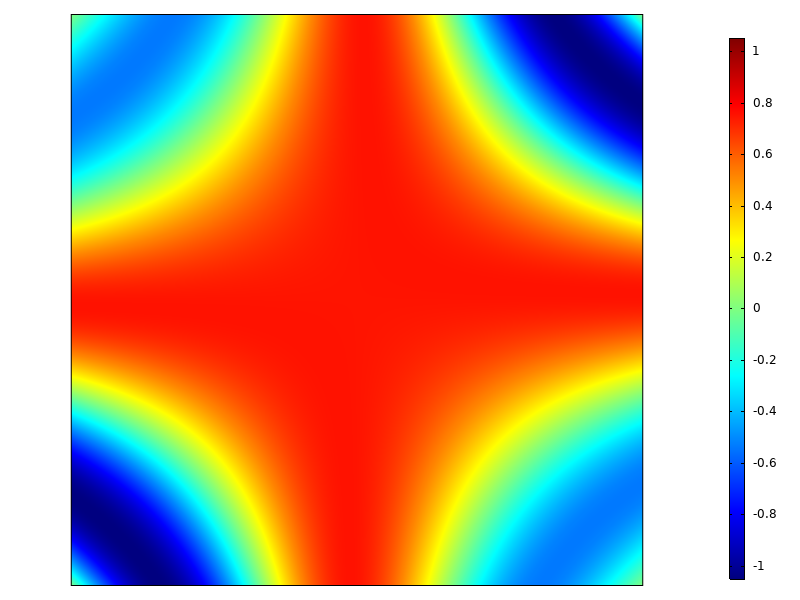
La fonction à intégrer.
Le tableau ci-dessous présente les résultats obtenus pour différents ordres de quadrature de Gauss. Dès que la fonction peut être raisonnablement approchée par un polynôme d’un certain degré, la valeur de l’intégrale converge rapidement.
| Points d’intégration | Précision | Ordre d’intégration | Valeur | Commentaires |
|---|---|---|---|---|
| 1 | 1 | 0 (ou 1) | 2.9958 | Utiliser uniquement la valeur au centre surestime nettement l’intégrale |
| 2×2 | 3 | 2 (ou 3) | 0 | Dans la règle des 2×2, les points de Gauss sont situés à \pm \frac{1}{\sqrt{3}}, où la fonction cosinus est égale à 0 (pas de chance !). |
| 3×3 | 5 | 4 (ou 5) | 1.1519 | |
| 4×4 | 7 | 6 (ou 7) | 0.9887 | |
| 5×5 | 9 | 8 (ou 9) | 1.0005 | |
| 6×6 | 11 | 10 (ou 11) | 1.0000 | |
| 7×7 | 13 | 12 (ou 13) | 1.0000 | |
| 8×8 | 15 | 14 (ou 15) | 1.0000 |
Le comportement optimal que présente la méthode de quadrature de Gauss pour les polynômes a toutefois un inconvénient : la méthode n’est pas très efficace pour intégrer des fonctions fortement discontinues. Supposons que nous voulions intégrer une fonction égale à f(x,y) = 1 lorsque y < ; -2x – 1 et 0 ailleurs sur le même carré que ci-dessus. Puisque la fonction vaut 1 sur un quart du carré et que le carré a une aire de 4, nous pouvons immédiatement voir que l’intégrale exacte doit valoir 1. Les résultats sont présentés dans le tableau ci-dessous.
| Points d’intégration | Valeur | Commentaires |
|---|---|---|
| 1 | 0 | Un seul point en (0,0), où la fonction est nulle |
| 2×2 | 1 | La fonction vaut 1 sur l’un des quatre points, avec une pondération de 1. |
| 3×3 | 0.8025 | La fonction vaut 1 en deux points dont les pondérations sont \frac{25}{81}, \frac{40}{81} |
| 4×4 | 1.2269 | La fonction vaut 1 en cinq points |
| 5×5 | 1.0325 | |
| 6×6 | 1.0918 | |
| 7×7 | 0.9892 | |
| 8×8 | 0.9961 |

Exemple avec 4×4 points d’intégration. La fonction vaut 1 dans le domaine orange. Les points verts sont les points de Gauss contribuant à la valeur de l’intégrale.
Comme le montre le tableau, il est difficile de calculer avec précision l’intégrale de cette fonction discontinue. Le hasard fait que le schéma d’intégration 2×2 donne la solution exacte, mais la convergence est loin d’être monotone.
Pourquoi est-ce important ? En analyse par éléments finis, on peut rencontrer des champs présentant des gradients locaux très marqués. C’est le cas par exemple des problèmes liés aux transformations de phase ou à la transition élastoplastique en mécanique des solides. Les intégrales calculées sur des éléments contenant ce type de variations soudaines peuvent présenter des erreurs significatives de discrétisation. La convergence de la solution peut également être affectée. De petits changements dans la solution peuvent modifier de manière importante les résidus calculés lorsque des points de Gauss individuels changent d’état.
Dans ce cas, il peut être préférable de sélectionner un ordre polynomial inférieur à l’ordre par défaut pour les fonctions de forme utilisées pour discrétiser le champ. La baisse de résolution peut être compensée par l’utilisation d’un maillage plus dense. En effet, les sauts inévitables seront limités à des éléments plus petits comportant moins de points d’intégration.
En outre, si vous calculez des intégrales de fonctions discontinues durant l’exploitation des résultats, il est important de garder à l’esprit la lenteur potentielle de la convergence de l’intégration numérique.
Intégration des contributions faibles
Dans chaque élément fini, diverses expressions doivent être intégrées pour constituer, par exemple, les matrices de rigidité, les matrices de masse, les vecteurs de chargement et les résidus. Si l’on prend l’exemple de la mécanique des solides, la formulation faible (ou variationnelle) standard correspond au principe des travaux virtuels : le travail virtuel effectué par les contraintes internes agissant sur une variation de déformation virtuelle est égal au travail virtuel des forces externes agissant sur la variation correspondante des déplacements virtuels.
Ici, le tilde (~) indique la variation virtuelle. Dans COMSOL Multiphysics®, c’est le rôle de l’opérateur test(). L’expression ci-dessus tient compte des forces volumiques, f, et des efforts surfaciques, t, mais il peut également y avoir d’autres types de contributions. Le membre de gauche contribuera à la matrice de rigidité, tandis que le membre de droite contribuera au vecteur de chargement (en supposant que les forces sont indépendantes des déplacements).
Pour accéder à l’implémentation des formulations éléments finis dans COMSOL Multiphysics®, il est nécessaire d’activer la Vue des équations.
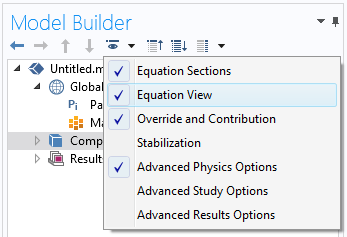
Activation de la Vue des équations.
Si nous examinons la Vue des équations d’une loi de comportement (par exemple, sous Matériau élastique linéaire) dans l’interface de Mécanique des solides, nous trouverons une section intitulée Expressions faibles listant les expressions utilisées pour construire diverses matrices, comme par exemple la matrice de rigidité.
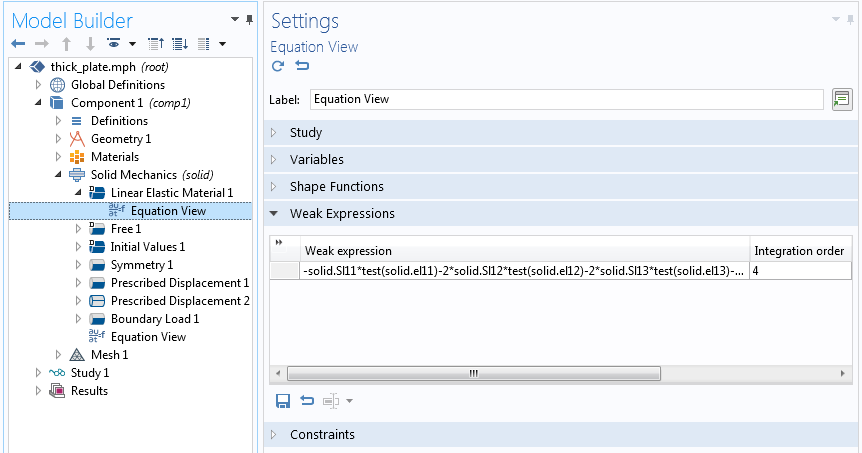
Expression faible pour le Matériau élastique linéaire dans l’interface de Mécanique du solide dans un cas stationnaire.
Dans la figure ci-dessus, vous pouvez observer un champ de saisie pour l’ordre d’intégration, qui, dans ce cas, contient la valeur 4. L’ordre d’intégration dans COMSOL Multiphysics® désigne l’ordre le plus élevé d’un polynôme pouvant être intégré de manière exacte. L’ordre d’intégration par défaut est basé sur l’ordre des fonctions de forme utilisées pour décrire le champ résolu (dans ce cas, les déplacements). Ici, l’ordre des fonctions de forme par défaut est quadratique, de sorte que les contraintes et les déformations auront une variation linéaire sur l’élément. Le produit de la variation des contraintes et des déformations est donc quadratique, ce qui indique que l’ordre 4 pourrait être plus que nécessaire. Nous verrons plus loin pourquoi cette valeur est sélectionnée.
En guise de second exemple, examinons un Chargement sur frontière en Mécaniques du solide.
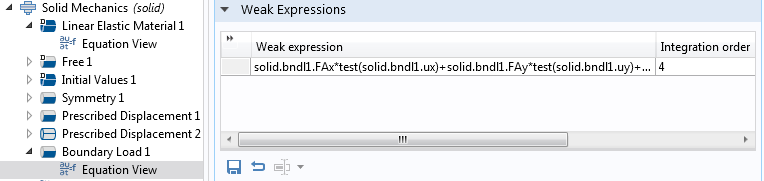
L’expression faible de la condition limite de Chargement sur frontière.
Ici aussi, l’ordre d’intégration est de 4. Sachant que les fonctions de forme du déplacement sont des polynômes quadratiques, cela signifie qu’il devrait être possible d’intégrer exactement la contribution d’un chargement dont la distribution présenterait une variation au plus quadratique, puisque le produit de l’effort surfacique et de la variation du déplacement serait alors d’ordre 4.
Quelques subtilités concernant les expressions faibles
La discussion précédente n’est strictement vraie que si les éléments ont des formes idéales (et ne présentent pas, par exemple, de frontières incurvées). Lorsque l’on se penche sur la théorie, on constate que les intégrales contiennent également un facteur d’échelle local (jacobien), qui décrit la transformation entre la géométrie réelle de l’élément et sa géométrie de référence. Si l’on calcule par exemple une intégrale sur un élément quadrilatère 2D, l’évaluation numérique est effectuée sur le carré idéal -1 ≤ ξ ≤ 1, -1 ≤ η ≤ 1,
Le jacobien sera, en général, une fonction rationnelle (polynômes au numérateur et au dénominateur). Il se peut donc qu’il ne soit pas exactement intégrable par ce type de quadrature numérique. C’est pourquoi il est judicieux de prévoir une certaine marge dans l’ordre d’intégration choisi. L’effet du jacobien est d’ailleurs l’une des raisons pour lesquelles les éléments fortement distordus donnent de moins bons résultats que ceux qui ont une forme idéale. Ce billet de blog sur l’inspection du maillage dans COMSOL Multiphysics® présente davantage d’informations sur la question de la qualité du maillage.
Bien qu’une fonction de forme soit dite “quadratique”, elle peut (dans certains cas) contenir des termes d’ordre supérieur. L’ordre indiqué dans l’interface utilisateur correspond au polynôme complet d’ordre le plus élevé dans les fonctions de forme. Le fait qu’il puisse y avoir des termes d’ordre supérieur dans ces polynômes est un argument supplémentaire en faveur de l’utilisation d’une règle d’intégration plus précise que celle qui semble nécessaire à première vue.
Il est également possible que l’ordre d’intégration soit plus élevé que prévu dans la Vue des équations pour une certaine contribution, afin d’assurer la symétrie d’une matrice de rigidité.
Modifier l’ordre d’intégration
Vous pouvez modifier l’ordre d’intégration de n’importe quelle expression faible à partir de la Vue des équations en modifiant le champ de saisie prévu à cet effet. Il y a deux raisons principales pour lesquelles vous pourriez être amené à faire une telle modification.
La première est la plus évidente : pour améliorer la précision. Considérons un chargement (au sens général ; il peut s’agir d’une force, d’un flux thermique, d’un courant électrique, etc.) présentant des variations importantes par rapport à la taille de l’élément. En augmentant l’ordre d’intégration numérique, on améliore la précision de la force ou du flux total appliqué sur le domaine. Cependant, la solution locale à proximité de la condition aux limites ne sera pas meilleure, car elle ne pourra jamais être plus précise que ce que les fonctions de forme de l’élément peuvent représenter.
Il existe cependant un autre cas intéressant : l’intégration réduite, qui signifie que l’ordre d’intégration, pour une raison quelconque, est inférieur à celui qui serait formellement nécessaire. L’une de ces raisons est l’accélération des calculs. Lors de la résolution d’un problème d’éléments finis, la majorité du temps CPU est consacrée à deux tâches : l’assemblage des matrices et la résolution de grands systèmes d’équations linéaires. Le temps consacré à la résolution des équations augmente plus rapidement que la taille du modèle, généralement comme le carré du nombre d’éléments. Le temps consacré à l’assemblage est directement proportionnel à la taille du modèle (plus précisément, au nombre d’éléments multiplié par le nombre de points d’intégration par élément). Pour un très grand modèle, la résolution des équations sera toujours dominante, mais pour les modèles non linéaires de taille moyenne comportant de lourds calculs en chaque point d’intégration, il peut être intéressant d’envisager l’utilisation d’une intégration réduite.
L’intégration réduite est également un outil numérique parfois utilisé pour supprimer la rigidité artificielle qui peut apparaître dans certaines formulations d’éléments par un phénomène connu sous le nom de locking. Un exemple d’utilisation de l’intégration réduite dans ce contexte peut être trouvé dans l’interface Coque en axisymétrie 2D. Dans les équations de travail virtuel, certains termes sont intégrés à l’ordre 2 et d’autres à l’ordre 4. Si l’intégration complète était utilisée partout, l’élément serait en fait beaucoup trop rigide pour une faible épaisseur de la coque. En utilisant une intégration réduite, certains termes problématiques dans l’énergie de déformation sont volontairement écartés.

Contributions des travaux virtuelles pour l’interface Coque en axisymétrie 2D.
Notes de l’auteur : la section suivante a été ajoutée le 4 mai 2023 pour inclure des informations sur les nouvelles fonctionnalités disponibles à partir de la version 6.0 de COMSOL Multiphysics®.
Intégration réduite
Certaines interfaces de Mécanique des structures proposent la possibilité de sélectionner l’intégration réduite directement à partir des paramètres de certaines lois de comportement.
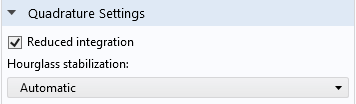
La section Paramètres de quadrature dans la fenêtre de réglages d’un Matériau élastique linéaire.
Cette approche présente plusieurs avantages par rapport au fait de modifier l’ordre d’intégration de la Vue des équations :
- La modification peut être effectuée en un seul endroit et elle se propage automatiquement à tous les sous-nœuds possibles.
- Vous n’avez pas besoin de savoir quel est le schéma d’intégration réduite approprié.
- Pour certaines fonctions de forme, la matrice de rigidité devient singulière si l’ordre d’intégration est réduit. Ceci est compensé par la fonctionnalité Stabilisation d’Hourglass .
- Certaines lois de comportement, comme la plasticité, ont des variables d’état locales qui sont stockées aux points d’intégration. Ces variables sont automatiquement synchronisées avec la règle d’intégration.
Opérateurs d’intégration
Sous le noeud Définitions dans le Constructeur de modèles, vous pouvez créer des opérateurs d’intégration. Ces derniers peuvent être utilisés pour définir des variables globales intervenant dans la formulation du problème, mais ils peuvent également être explicitement utilisés dans des expressions lors de l’évaluation des résultats.
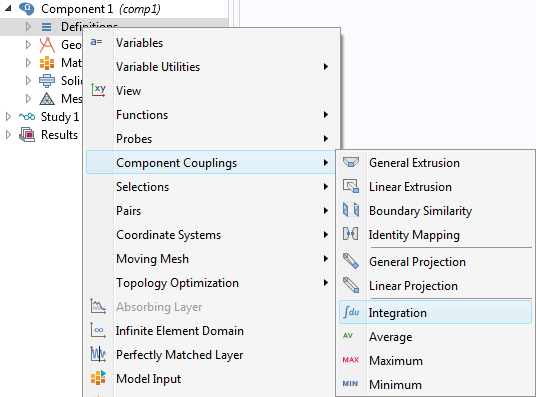
Ajout d’un opérateur d’intégration.
Au moment de l’ajout d’un opérateur d’intégration, les trois principaux choix à effectuer sont les suivants :
- Les domaines, les frontières ou les arêtes sur lesquels l’intégrale doit être réalisée.
- L’ordre d’intégration – Cela vous offre également la possibilité de privilégier la précision ou la rapidité. Notez que l’intégrande réelle n’est pas seulement l’expression que vous fournissez, mais qu’elle est également multipliée par le jacobien, décrivant la transformation de la forme de référence à la forme réelle de l’élément.
- Le repère – Ce point ne devient important que lorsque différents repères existent, comme dans le cas d’un maillage mobile, d’une géométrie déformée et d’une non-linéarité géométrique en mécanique des structures. En d’autres termes : l’intégrale doit-elle être calculée sur une géométrie déformée ou non déformée ?
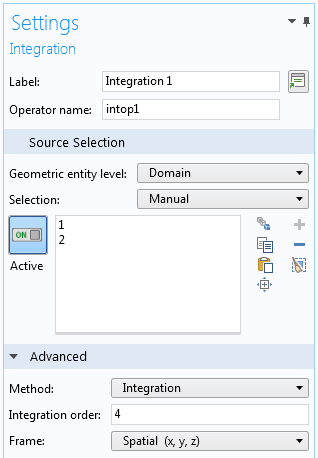
Fenêtre de réglages d’un opérateur d’intégration.
Intégration durant l’exploitation des résultats
Lorsque vous souhaitez calculer une intégrale durant la phase d’exploitation des résultats, deux options s’offrent à vous : utiliser un opérateur d’intégration (comme décrit ci-dessus) ou ajouter un nœud Intégration sous Quantités dérivées. Dans une large mesure, le choix est arbitraire. Cependant, dans le nœud Intégration, vous ne pouvez pas sélectionner explicitement le repère utilisé pour l’intégration ; il est déduit de la sélection du référentiel dans le nœud Solution.
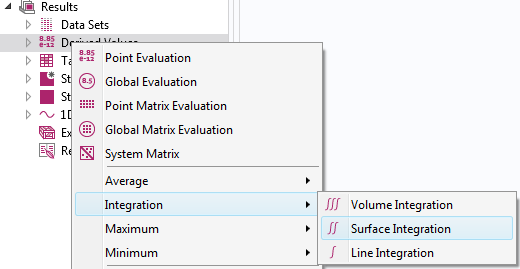
Ajout d’un nœud d’intégration lors de l’exploitation des résultats.
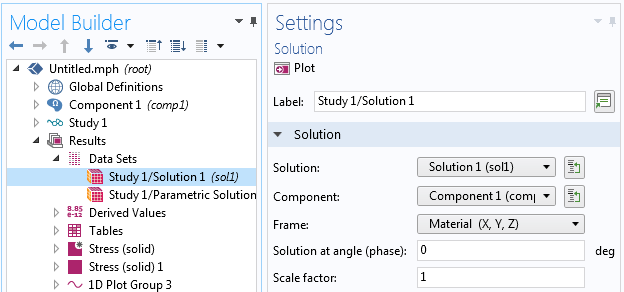
Fenêtres de réglages d’un jeu de données permettant de sélectionner le référentiel utilisé pour l’évaluation des résultats.
Si la sélection du référentiel est importante, vous devriez plutôt vous appuyer sur les opérateurs d’intégration pour éviter tout risque d’erreur. Si vous ajoutez un opérateur d’intégration après avoir résolu le problème, il est important de Mettre à jour la solution afin que le nouvel opérateur soit accessible.
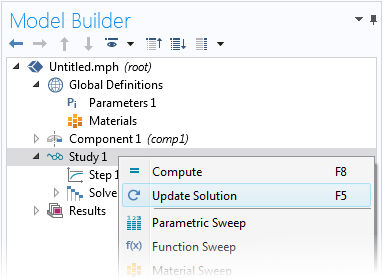
Mise à jour d’une solution.
N’oubliez pas de choisir un ordre d’intégration suffisamment élevé. Il convient en particulier d’être prudent si les expressions à intégrer sont fortement non linéaires ou discontinues. Les expressions booléennes constituent un cas particulier courant d’expressions discontinues. Par exemple, si après une analyse de transfert de chaleur, vous souhaitez calculer le volume dans lequel la température est supérieure à une certaine valeur, vous pouvez utiliser comme intégrande T>1066[K]. Cette expression vaudra 1 là où la condition est respectée et 0 ailleurs, de sorte que son intégration donnera le volume de la zone pour laquelle la condition est satisfaite. Cependant, la frontière entre les deux valeurs traversera généralement des éléments.
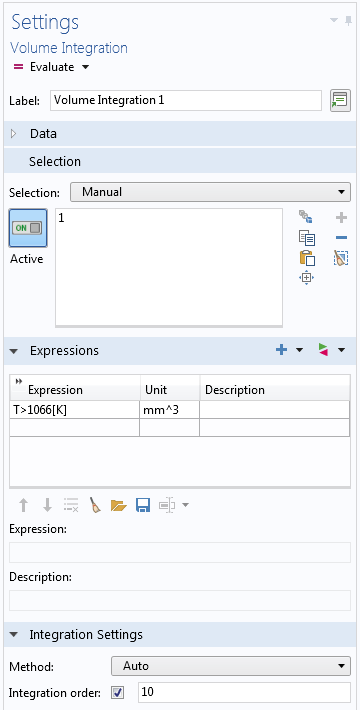
Intégration d’une expression booléenne avec une plus grande précision d’intégration.
Fonctions de forme des points de Gauss
Lorsque vous enrichissez votre modèle multiphysique, vous devez parfois ajouter des degrés de liberté définis par l’utilisateur (variables dépendantes). Pour ce faire, vous devez sélectionner le type de fonction de forme utilisé pour les représenter. L’une des options est Données au point de Gauss. Toutes les autres options donnent différents types de champs qui ont une distribution continue sur l’élément et peuvent ou non être continus entre des éléments adjacents. Le type de fonction de forme données au point de Gauss est fondamentalement différent. Il ne stocke qu’une valeur à chaque point de Gauss, sans aucun lien avec des valeurs situées ailleurs dans l’élément.
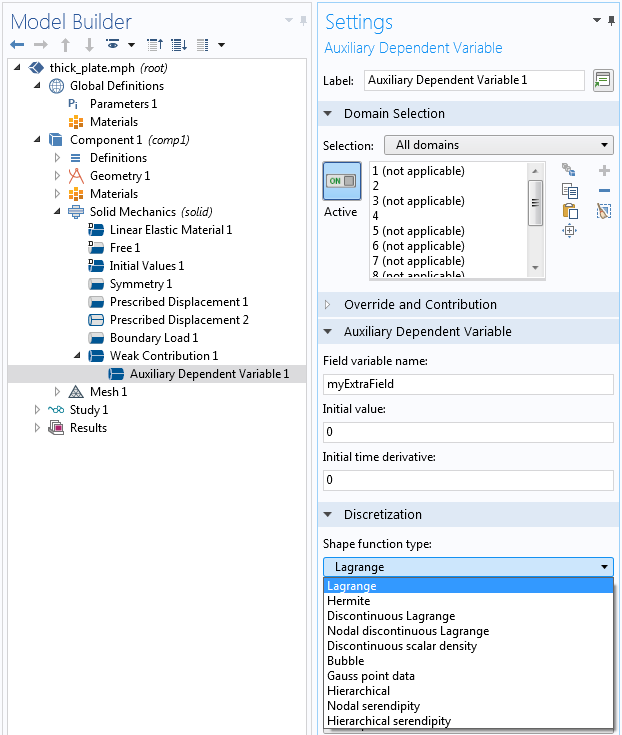
Sélection du type de fonction de forme pour une variable dépendante définie par l’utilisateur.
Le type Données au point de Gauss est utile lorsque vous souhaitez stocker un état local. Cela peut être le cas, par exemple, dans les modèles constitutifs non linéaires dépendant de l’historique et nécessitant une “mémoire”. Le modèle constitutif est principalement consulté lors du calcul des matrices de rigidité et des résidus, de sorte que les seuls endroits de l’élément où il sera réellement évalué au cours de la résolution sont les points d’intégration. Il est donc logique de stocker ce type de données à cet endroit précis.
Un exemple d’utilisation interne des données au point de Gauss est le stockage des déformations inélastiques dans les lois de comportement telles que la plasticité et le fluage en mécanique des structures.
Une fois que vous avez décidé de stocker des données aux points de Gauss, vous devez sélectionner l’Ordre des éléments, qui correspond à l’ordre d’intégration, comme discuté ci-dessus. Le coût (en termes de mémoire et de temps CPU) du stockage des données aux points de Gauss est proportionnel à l’ordre sélectionné en 1D, à son carré en 2D et à son cube en 3D.
Sélection de l’ordre d’intégration au point de Gauss.
Si vous ajoutez des variables aux points de Gauss dans une interface physique prédéfinie, vous devez généralement sélectionner le même ordre d’intégration que celui utilisé pour calculer les expressions faibles correspondantes. En cas de non-concordance, les valeurs devront être évaluées à différents endroits de l’élément, ce qui entraînera une perte de précision et de performance.
L’opérateur gpeval
Lorsque des variables sont stockées aux points de Gauss, qu’elles soient prédéfinies ou définies par l’utilisateur, il peut arriver que vous ayez besoin de les interpoler sur l’élément. Ceci est particulièrement important lors de l’exploitation des résultats. Par défaut, lorsque des variables définies aux points de Gauss sont évaluées à un autre endroit de l’élément, on reprend simplement la valeur au point de Gauss le plus proche. L’opérateur gpeval() peut être utilisé pour convertir les données discrètes des points de Gauss en un champ continu. Dans sa version la plus simple, l’opérateur est appelé par l’expression gpeval(gporder, expression), par exemple, gpeval(4,solid.epe). Pour plus de détails, veuillez vous référer au Guide d’utilisation de COMSOL Multiphysics®.
Prenons l’exemple suivant : la coordonnée x (variant entre 0 et 3) est stockée sous forme de données aux points de Gauss dans un petit modèle à trois éléments. Pour ce faire, on ajoute une variable dépendante auxiliaire, comme indiqué ci-dessous.
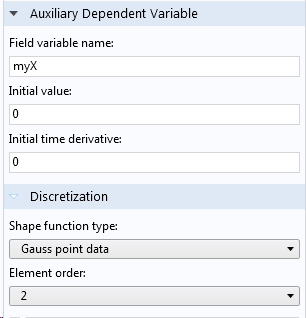
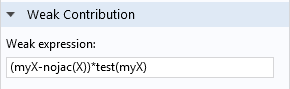
Stockage de la coordonnée x comme une donnée au point de Gauss.
La contribution faible (myX-nojac(X))*test(myX) énonce simplement : “Fixer la variable myX à la valeur actuelle de X.” L’opérateur nojac() est utilisé pour éviter un couplage bidirectionnel entre myX et X. Il convient de l’utiliser lorsque vous souhaitez simplement attribuer une valeur à une variable dépendante.
Si la variable définie au point de Gauss myX est ensuite représentée dans un graphique de surface (sans calcul de moyenne entre les éléments), le résultat sera discontinu. Dans chaque élément, les variables aux point de Gauss sont déplacées vers le coin le plus proche, puis interpolées sur l’élément. Si, au lieu de cela, l’expression gpeval(2,myX) est utilisée, nous récupérons la distribution exacte de la coordonnée x.
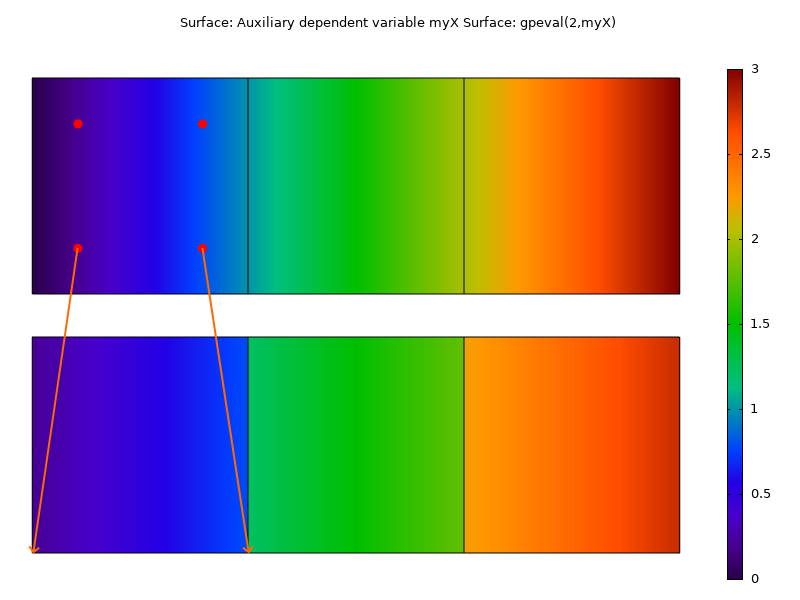
Graphique de la variable au point de Gauss (en bas) et de la même variable extrapolée (en haut). Les flèches indiquent comment les données aux points de Gauss sont déplacées par défaut vers les coins lors de l’évaluation des résultats.
Prochaine étape
Pour en savoir plus sur les fonctionnalités disponibles dans le logiciel COMSOL®, cliquez sur le bouton ci-dessous :




Commentaires (0)