
Dans les simulations d’écoulements de fluides, il est souvent important d’évaluer les forces que le fluide exerce sur le corps — par exemple, les forces de portance et de traînée sur un profil d’aile ou autour d’un véhicule. Les ingénieurs peuvent utiliser ces forces appliquées sur le corps pour quantifier l’efficacité et les performances aérodynamiques des modèles. Aujourd’hui, nous allons aborder différentes façons de calculer la portance et la traînée dans COMSOL Multiphysics®.
Définition de la portance et de la traînée
Lorsqu’un écoulement de fluide passe autour d’un corps, il exerce une force sur sa surface. Comme le montre la figure ci-dessous, la composante de la force qui est perpendiculaire à la direction de l’écoulement est appelée portance. La composante de la force qui est parallèle à la direction de l’écoulement est appelée traînée. Pour simplifier, supposons que la direction de l’écoulement est alignée sur le système de coordonnées du modèle. Plus tard, nous allons vous montrer comment calculer les forces de portance et de traînée selon une direction qui n’est pas alignée avec le système de coordonnées du modèle.
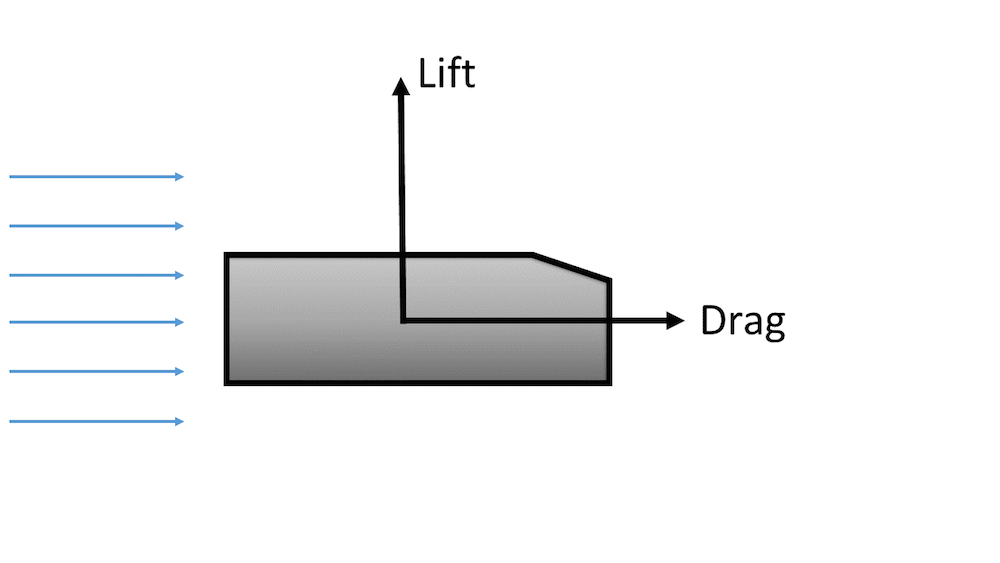
Schéma des composantes de la portance et de la traînée lorsqu’un écoulement fluide passe autour d’un corps.
Il y a deux facteurs distincts qui contribuent aux forces de portance et de traînée — la force de pression et la force visqueuse. La force de pression, souvent appelée force de gradient de pression, est la force due à la différence de pression à travers la surface. La force visqueuse est la force due à la friction qui agit dans la direction opposée de l’écoulement. Les amplitudes de la force de pression et de la force visqueuse peuvent varier considérablement selon le type d’écoulement. L’écoulement autour d’une voiture en mouvement, par exemple, est souvent dominé par la force de pression.
Calcul de la portance et de la traînée à l’aide de la contrainte totale
COMSOL Multiphysics® offre un accès complet à toutes les variables internes et permet de calculer très facilement les forces de surface par intégration sur une frontière. Ici, nous allons montrer comment calculer les forces de traînée sur un corps d’Ahmed. Vous pouvez télécharger ce modèle à partir de notre Bibliothèque d’Applications.

Simulation d’un écoulement d’air autour d’un corps d’Ahmed. Le graphique de surface montre la distribution de la pression et les lignes de courant sont colorées par la norme de la vitesse. La surface fléchée derrière le corps d’Ahmed montre la recirculation dans le sillage.
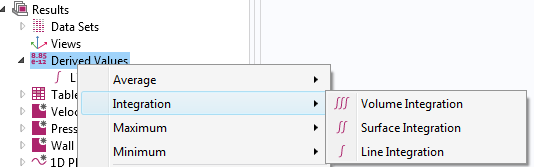
Il existe plusieurs façons de calculer la traînée en fonction de la physique. La méthode la plus simple consiste à intégrer la contrainte totale — qui comprend les contributions de la force de pression et des forces visqueuses — dans chaque direction. Pour ce faire, nous devons d’abord définir un opérateur d’intégration de surface sous le nœud Quantités dérivées, comme illustré ci-dessous.
ASTUCE : Alternativement, il est également possible d’utiliser une sonde sur frontière ou un opérateur d’intégration dans les couplages non locaux pour définir une telle intégration. La différence est que les opérations définies dans les réglages des physiques peuvent être utilisées pendant la simulation — par exemple, la force de traînée calculée avec une sonde sur frontière comme objectif ou contrainte dans une étude d’optimisation.
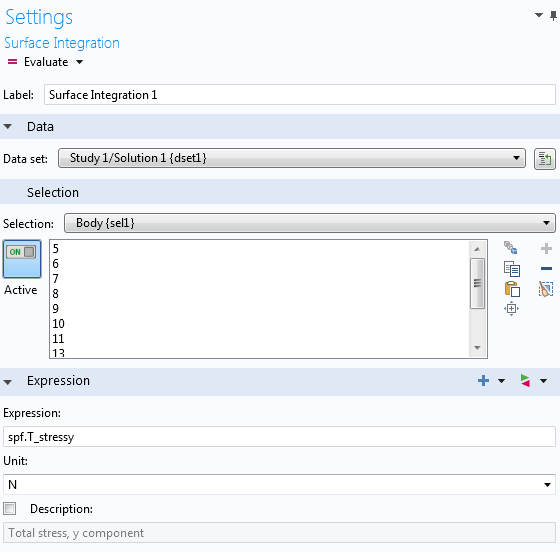
Ensuite, nous pouvons sélectionner les frontières sur lesquelles effectuer l’intégration. Dans cet exemple, nous avons choisi toutes les frontières du corps. Dans ce modèle, le déplacement se fait dans la direction y. Nous pouvons taper l’expression : spf.T_stressy, qui représente la contrainte totale dans la direction y.
Calculer séparément la force de pression et la force visqueuse
Parfois, les ingénieurs peuvent obtenir un meilleur aperçu des modèles en examinant séparément la force de pression et la force visqueuse. COMSOL Multiphysics® propose une variable prédéfinie, spf.K_stressy, pour la contrainte visqueuse dans la direction y. Nous pouvons facilement évaluer la force visqueuse en intégrant la contrainte visqueuse.
Qu’en est-il de la force de pression ? La pression, désignée par la variable p, est un scalaire. Pour la projeter dans la direction de la traînée, nous devons multiplier la pression par la composante y du vecteur normal à la surface, spf.nymesh. Par conséquent, nous pouvons évaluer la force de pression en intégrant spf.nymesh*p sur la surface.
Dans certains cas particuliers d’écoulements turbulents où une loi de paroi est utilisée, il est plus précis de calculer la force visqueuse en utilisant la vitesse de frottement, spf.u_tau. Dans COMSOL Multiphysics®, les modèles de turbulence k-epsilon et k-omega font appel à une telle loi de paroi.
Pour en apprendre davantage au sujet des modèles de turbulence dans COMSOL Multiphysics®, lisez notre article de blog “Which Turbulence Model Should I Choose for My CFD Application?”.
Nous pouvons obtenir la contrainte de cisaillement locale au niveau de la paroi par :
Par conséquent, la contrainte de cisaillement locale dans la direction y est :
où u^T est la vitesse tangentielle à la paroi. Nous pouvons encore réécrire u^T en u_\tau*u^+, où u^+ est la vitesse tangentielle adimensionnalisée.
Sans entrer trop dans les détails sur la dérivation, nous pouvons traduire les équations précédentes en variables COMSOL. Nous intégrons la contrainte de cisaillement locale de la paroi dans la direction de la traînée (la direction y) avec l’expression suivante : spf.rho*spf.u_tau*spf.u_tangy/spf.uPlus. Dans cette expression, spf.rho est la densité du fluide, spf.u_tangyy à la paroi et spf.uPlus est la vitesse tangentielle adimensionnalisée.
Le tableau ci-dessous résume les expressions utilisées pour calculer chaque force.
| Écoulement fluide sans loi de paroi | Écoulement turbulent avec loi de paroi | |
|---|---|---|
| Force de pression | spf.nymesh*p | spf.nymesh*p |
| Force visqueuse | -spf.K_stressy | spf.rho*spf.u_tau*spf.u_tangy/spf.uPlus |
| Force totale | -spf.T_stressy | spf.nymesh*p + spf.rho*spf.u_tau*spf.u_tangy/spf.uPlus |
Note : Dans cet exemple, la force de traînée est dans la direction y. Vous devrez peut-être modifier la direction de projection en fonction de l’orientation de votre modèle.
Correction de l’angle d’attaque
Il est fréquent que la géométrie ne soit pas parfaitement alignée avec la direction de l’écoulement. L’angle entre la ligne de référence centrale de la géométrie et le l’écoulement incident est appelé angle d’attaque (souvent désigné par la lettre grecque \alpha). En ingénierie aérospatiale, l’angle d’attaque est fréquemment utilisé car il s’agit de l’angle entre la corde de l’aile et la direction d’écoulement libre. La figure suivante montre la relation entre la portance, la traînée et l’angle d’attaque d’un profil d’aile.
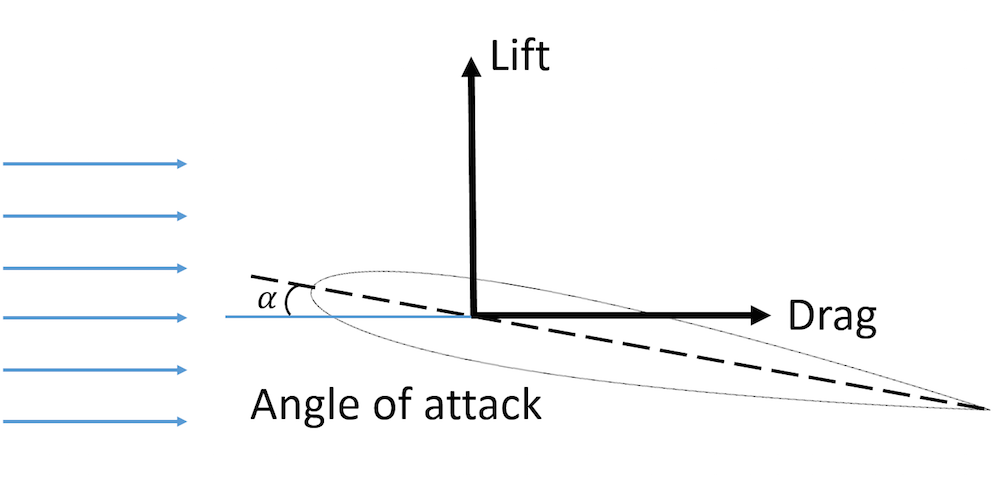
Schéma illustrant la portance, la traînée et l’angle d’attaque d’un profil d’aile.
En utilisant un modèle 2D NACA 0012, nous allons vous montrer comment calculer la portance avec une correction sur l’angle d’attaque. Ce modèle est disponible en téléchargement dans la Bibliothèque d’Applications.
Il y a deux façons de modifier l’angle d’attaque du modèle. Nous pouvons soit faire tourner la géométrie elle-même, soit garder la géométrie fixe mais modifier la direction de l’écoulement à l’entrée. Ici, nous utiliserons la deuxième approche. Il est beaucoup plus simple d’ajuster le champ de vitesse imposé par la condition limite d’entrée car nous n’aurons pas besoin de remailler le modèle pour chaque angle d’attaque. Comme le montre la figure ci-dessous, l’aile est fixe tandis que les lignes de courant montrent l’écoulement à un angle d’attaque induit par l’ajustement de la direction de la vitesse d’entrée.
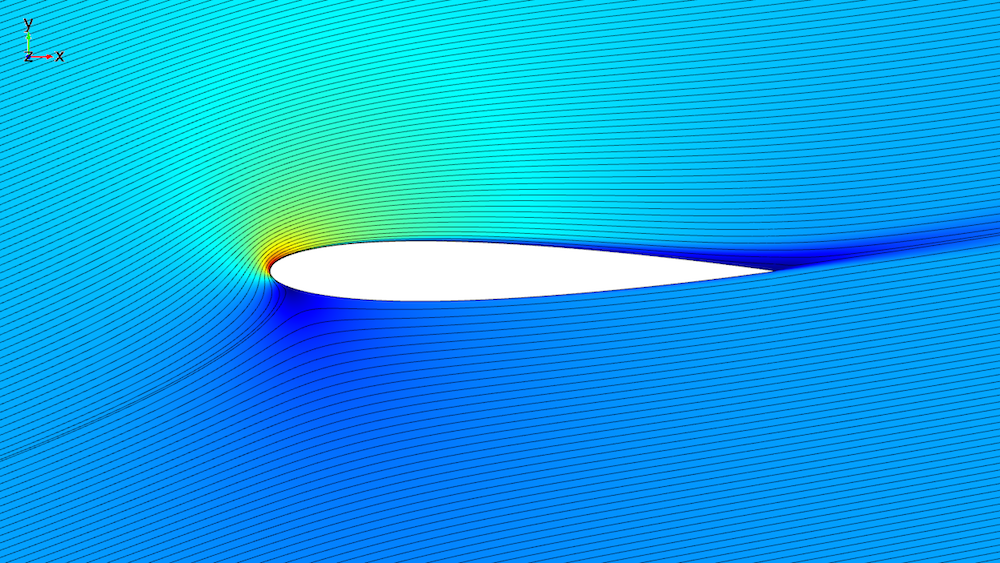
Simulation d’un écoulement passant autour d’un profil NACA 0012 à un angle d’attaque de 14 degrés. Le graphique de surface montre la norme de la vitesse ainsi que les lignes de courant (en noir).
Cet exemple fait appel au modèle de turbulence SST, qui n’utilise pas de loi de paroi. Par conséquent, nous utiliserons la contrainte totale pour calculer la portance. A un angle d’attaque nul, la portance est simplement -spf.T_stressy. Si l’angle d’attaque est non nul, nous pouvons projeter la force sur la direction de la portance en utilisant l’expression suivante : spf.T_stressx*sin(alpha*pi/180)-spf.T_stressy*cos(alpha*pi/180). Ici, alpha représente l’angle d’attaque en degrés.
Qu’en est-il des coefficients de portance ou de traînée ?
Vous pouvez également être intéressé par les formes adimensionnées de la portance et de la traînée – le coefficient de portance et le coefficient de traînée. Il est souvent plus facile d’utiliser les coefficients plutôt que les forces dimensionnelles dans le but de valider les données expérimentales ou de comparer différents modèles. Le coefficient de portance en 2D est défini comme suit :
Puisque nous avons déjà calculé la force de portance dimensionnelle, nous pouvons simplement normaliser la portance par la pression dynamique et la longueur de corde. Avec le coefficient de portance adimensionné, nous pouvons comparer nos résultats de simulation avec les données expérimentales (Ref. 1).
Note : En 3D, le coefficient de portance est adimensionné par la surface au lieu de la longueur : C_L = \frac{L}{\frac{1}{2} \rho u^2_\infty A}
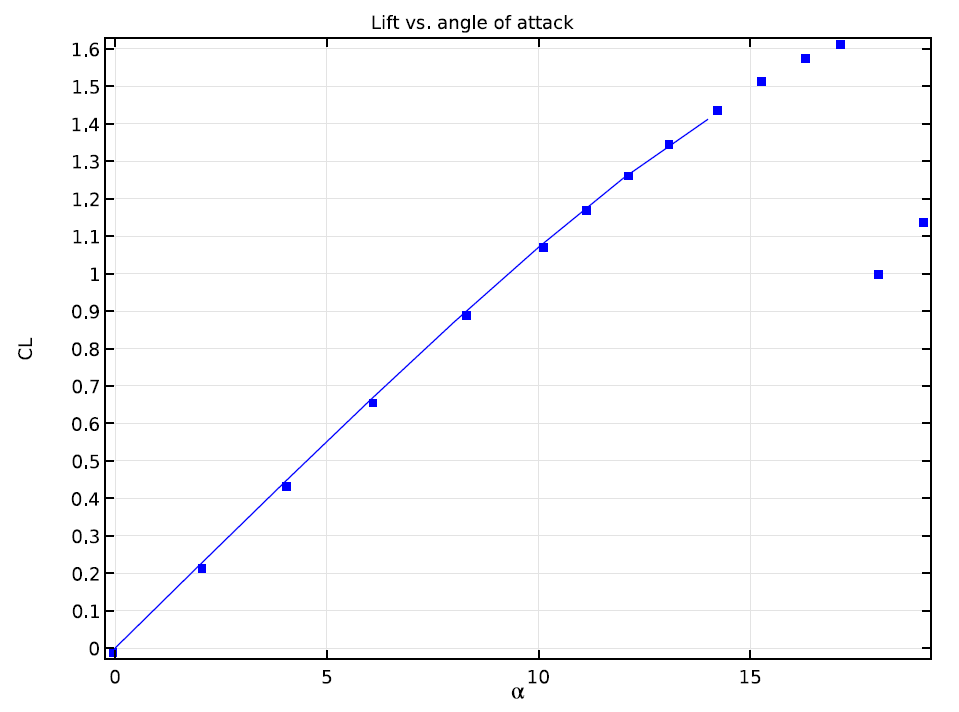
Graphique comparant les résultats d’une simulation et les données expérimentales du coefficient de portance sur un profil NACA 0012 pour différents angles d’attaque.
Comme le montre le graphique ci-dessus, il n’y a pas d’écart notable entre les résultats de calcul et les résultats expérimentaux dans la plage de valeurs d’angle d’attaque utilisée dans cette simulation. Les résultats expérimentaux continuent vers un régime d’angle d’attaque élevé jusqu’au décrochage de l’aile.
Remarque de conclusion
Dans cet article de blog, nous avons exploré les moyens de calculer la portance et la traînée d’un corps d’Ahmed et d’un profil d’aile NACA 0012. Nous avons montré comment calculer la force de pression et la force visqueuse, tout en examinant le cas particulier où une loi de paroi est utilisée par le modèle de turbulence.
Chacune des approches que nous avons présentées ici n’est certainement pas limitée à ces simulations spécifiques. Vous pouvez calculer les forces sur n’importe quelles frontières ou surfaces et ainsi mieux comprendre les modèles grâce aux simulations multiphysiques. Avec le Module Optimization, vous pouvez aller plus loin dans cette analyse et optimiser la portance ou la traînée.
Références
- C.L. Ladson, “Effects of Independent Variation of Mach and Reynolds Numbers on the Low-Speed Aerodynamic Characteristics of the NACA 0012 Airfoil Section,” NASA TM 4074, 1988.



Commentaires (0)